数形结合思想在高中数学教学中的应用策略浅析

耿开鹏

◆摘  要：“数形结合思想”是高中数学中常见的数学思维，能够将原本抽象的问题形象化和具体化，将复杂繁琐的问题赋予灵活变通的形式，实现学生思维的迁移，进而学会利用数形结合解决数学难题，对提升解题效率有着重大意义。基于此，本文从高中数学中应用“数形结合思想”的必要性出发，提出了针对性的优化运用策略，让学生能够快速、有效的解决实际问题。

◆关键词：数学结合思想;高中数学;应用策略

数形结合思想的关键在于“数”和“形”的灵活转换，需要学生具备灵活的思维，因此，高中数学教学应该是富有探究性的，教师只有深刻践行“数形结合思想”、将不同数学理念教学融入课程中，才能培养出学生灵活的思维方式，促进学生加深对数学知识的吸收和理解，实现学生思维能力、知识应用水平的全面提升。

一、数形结合思想在高中数学教学中应用的意义

1.有利于提高解题效率。高中数学相对于初中的教学内容和难度进一步提升，其计算过程更为繁琐，因此，高中数学的解题过程并非一成不变的。例如在几何知识的讲解时，部分面积、体积问题都可以利用特定的公式解决，但多数大题通常会呈现出不规则图形，学生缺乏有效的解题思维和数学思维，在解答过程中难以实现公式或者定理的灵活运用，进而无法有效解决几何问题。因此，如果学生不具备“数形结合思想”，则难以有效解决几何题。

2.让抽象的知识直观化。应用“数形结合思想”能够让学生将原本抽象的问题形象化和具体化，实现“数”和“形”的任意转化，进而促使学生的思维迁移。例如对于同一类型的数学题，只是换了题干，许多学生就难以识别和解答，但是如果学生具备较强的数学思维，脑海中第一闪现出的就是利用“数形结合思想”解答，立马就明白了题目的考察点，进而快速的解答问题。

二、数形结合思想在高中数学教学中应用存在的问题

当下高中数学中仍然存在“教条式”教学，存在一定的盲目性和形式性，即使部分教师渗透数形结合思想，也通常表现为一带而过，没有进行深度讲解数形结合思想的运用原则，学生无法掌握其内涵，具体而言，数形结合思想教学的问题主要表现在以下几个方面：首先，教师一味的讲解教材定理和规律，忽略了对教学的内容的拓展和变通。其次，没有深刻意识到数形结合思想的重要性，只停留在数和形的互译，通常只是给学生传递解题过程和结果，对于“数”如何转化为“形”没有阐明。最后，教师缺乏构图意识，在教学中，教师很少在黑板上绘图，数形结合思想的应用不够直观，难以为学生呈现出良好的数形转换讲解，以致于学生遇到问题，同样缺乏构图意识，不能在第一时间想到利用数形结合思想解答。

三、数形结合思想在高中数学教学中的应用策略

1.发挥出教师的引导作用，深刻践行数形结合思想。高中数学知识对于学生而言需要较强的理解能力，需要教师正确的引导，注重自主探究，让学生在探究过程中自行探索、自行思考，教师只是作为引导者或者解惑者，通过教师引导和学生自主探究，有效实现数形结合思想的渗透。所以在数形结合思想灌输時，老师要循序渐进的引导，给学生讲解数形结合思想的运用原则，不能直接告诉学生答案，或者告诉学生采用何种思维，而是在教师的引导下一步步的找出突破口，让学生有迹可循。例如在函数f（x）=（x+1）（x+2）的值域求解时，学生可以根据函数内容进行坐标图绘制，将抽象的函数转化为斜率范围中的数学问题，进而快速获取答案。其次，在正弦、余弦求解时，教师也可以进行数形体结合思想的渗透，如在求正弦、余弦值时，可以在角终边线取一点P（1，y），在直角三角形PAO内，AO=1，此形况下P（1，y）为？这类函数图通过画图画辅助线的方式，能够轻松得出答案。总之，高中数学教学中应用数学思想之处众多，几乎每一单元都含有“数”和“形”之间的转换，教师在实际教学中，要加强这些思想的传递，为学生今后有效解决数学问题奠基。

2.选择典型例题，培养学生的思维能力。数形结合思想渗透最好的方式就是培养学生的自主探究能力，而要想培养学生的自主探究能力，教师可以在数学课堂中提出一些具有典型性的问题，让学生带入到数学知识探索当中去，培养出他们独立思考的能力。比如一例题为：方程x?-4x+3=m有四个根，则求实数m的取值范围。这道题就是利用数形结合思想极大的典型例题，方程x?-4x+3=m的根的个数就是函数y=x?-4x+3与函数y=m图像的交点的个数，此刻画出抛物线y=x?-4x+3=（x-2）?-1的图像，将x轴下方的图像沿着x轴翻折得到y=x?-4x+3，再作直线y=m，通过直观观察图像迅速得答案m的取值范围为（0，1）。需要注意的是，在习题讲解过程中，教师也要树立构图意识，在黑板上经常性构图，让学生的思维可视化。

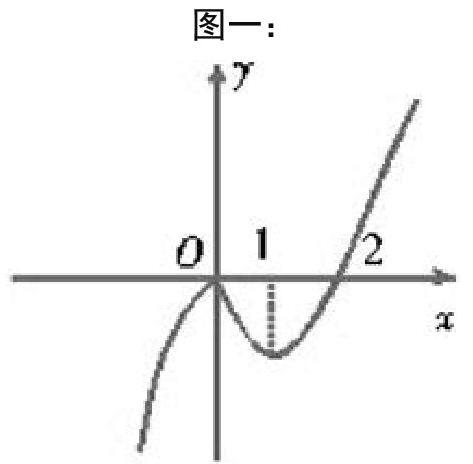
3.结合数形结合思想有效解答函数类问题。函数是高中数学的重点组成，也是需要重点应用数形结合思想的习题类型之一，在函数类例题中，教师要引导学生遵循数形结合思维，让学生迅速解答函数问题。例如在函数f（x）=值域求解时，要根据函数内容进行坐标图绘制，将抽象的函数转化为斜率范围中的数学问题，进而快速获取答案。此外，数形结合思想也可用于正弦、余弦求解，如在求正弦、余弦值时，可以在角终边线取一点P（1，y），在RT三角形PAO内，AO=1，此形况下P（1，y）为，这类函数图通过画图化辅助线的方式，能够轻松得出答案。此外，数形结合也可用于单调区间问题，如一函数为确定y=x丨x丨-2丨x丨的单调区间，画出函数草图（如图一），直观得出答案y=x丨x丨-2丨x丨=x?-2x，x≥0或者-x?+2x，x<0，快速得到单调递增区间为区间为（-∞，0]，[1，+∞）。单调递减区间为[0，1]。

四、总结

数形结合思想是数学学习中最为基本、也是最为重要的思维方法，借助于“数”和“形”的转化，将复杂的问题直观化，让学生能够巧妙解答。因此，教师要深刻意识到数形结合思想的重要性，不仅要注重题型的讲解，还要注重数形结合思想的培养，让学生深刻意识到数形结合思想的优越性，在解决实际问题时首先想到的就是数形结合思想。

参考文献

[1]刘燕.试析数形结合思想在高中数学教学中的应用[J].新课程教学（电子版），2019（02）：45.

[2]姚晶月.浅析数形结合思想在高中数学教学中的应用策略[J].考试周刊，2020（74）：79-80.

[2]金家庆.数形结合思想在高中数学教学中的应用策略探究[J].考试周刊，2020（75）：53-54.