气穴和圆度误差影响下滑动轴承润滑静特性分析*
贾晓波 师占群 张 浩 甄 冬 李 鹏
(河北工业大学机械工程学院 天津 300130)
在精密的旋转机械设备中,滑动轴承作为其关键部件有着很高的旋转精度,同时也会受到润滑油密度、黏度、温升和轴承加工精度因素的影响。学者们对滑动轴承的气穴、热效应、圆度误差等方面进行了深入研究。GRANDO等[1]建立了考虑油膜空化影响的滑动轴承数学模型,分析了在平衡条件和非平衡条件下的滑动轴承油膜特性,发现两者之间存在较大差异。王树圣[2]通过建立气穴和热效应相关数学模型,并求解变密度和变黏度的Reynolds方程和能量方程,研究发现端泄流量受气穴和热效应影响较大。陈荣尚[3]通过对考虑气穴因素和表面粗糙度的Reynolds方程进行耦合分析,再用有限差分法进行求解,分析得到在这两者因素影响下,油膜静动特性参数以及稳定性参数变化规律。张一磊等[4]通过引入加工误差中的随机圆度误差和椭圆圆度误差因素,代入油膜厚度公式进行求解,研究其对滑动轴承的影响。向建华等[5]将椭圆和齿形圆度误差因素代入油膜厚度公式,并研究这些因素在不同偏心率下对转子系统的承载力系数、端泄流量、能量损失的影响。杨小高[6]在传统油膜的理论基础上考虑尺寸和形状误差等加工因素,建立起考虑这两者因素的累积效应数学模型,研究发现混合节流油膜轴承能较好减小加工误差的影响。吉宏斌等[7]建立气穴的椭圆轴受力模型,用Fluent模拟分布,仿真分析得出有无气穴状态下和不同轴颈转速下油膜压力分布规律,但是该文献只是在椭圆轴承的基础上研究气穴的影响,并未具体研究圆度误差的影响。师占群等[8]研究发现在热效应和弹性变形耦合下,浮环轴承承载力、摩擦功耗、端泄流量降低。卢黎明和谷开[9]以滑动轴承为研究对象,研究发现黏度增加将加剧楔形区域发散区的空化现象,增大承载力,降低稳定性。刘黄亮[10]基于滑动轴承,建立三维两相流的数学分析模型,通过数学计算探究表面织构的影响规律,发现布置在空化区的表面织构会增强局部空化作用,且随着织构面积率增加,润滑性能变好。吴超等人[11]对计入气穴影响的滑动轴承进行Fluent仿真分析,得出最大压力和承载力随转速和长径比的增加而增加。张绿野[12]对滑动轴承进行三维模型设计,并通过滑动轴承静力特性试验得到油膜压力与转速大小成反比关系,与载荷大小成正比关系的结论。牛嘉彬[13]采用Fluent分析滑动轴承的两相流流场,基于滑动轴承的气穴效应搭建滑动轴承实验台,并用高速相机拍摄油膜中气泡变化规律,通过与仿真数据对比,验证仿真分析的有效性。
综上所述,目前的研究并没有综合考虑气穴和圆度误差2种因素作用下对滑动轴承润滑特性的影响。而当滑动轴承在高速旋转时,润滑油难免会产生气泡;由于滑动轴承加工精度的限制,圆度误差的存在也是难免的,因此综合考虑两者的影响很有必要。本文作者将考虑轴颈和轴瓦圆度误差和考虑气穴黏度和密度变化的方程联立,得到考虑气穴和圆度误差影响的耦合雷诺方程,并通过迭代求解油膜压力等静特性参数,分析气穴和圆度误差对滑动轴承静特性参数的影响。
1 滑动轴承数学模型
1.1 标准滑动轴承动力学模型
对于普通的滑动轴承,其油膜间隙示意图如图1所示。图中R为轴瓦半径,r为轴颈半径,Ob为轴瓦圆心,Oj为轴颈圆心,e为偏心距,φ为位角,hmax为最大油膜间隙,hmin为最小油膜间隙,ωj为轴颈旋转角速度。
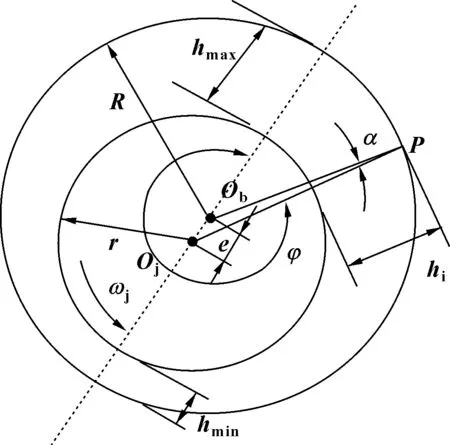
图1 轴承油膜间隙
如图1所示,点P到轴颈中心距离为
r+hi=ecosφ+Rcosα
(1)
点P处轴承油膜厚度可以表示为
(2)
偏心距e可忽略不计。所以油膜厚度为
hi=R-r+ecosφ=h0(1+εcosφ)
(3)
式中:φ为位角;h0为间隙;ε为偏心率。
1.2 普通雷诺方程
普遍形式的雷诺方程:
(4)
引入量纲一化因子:
量纲一化雷诺方程如下:
(5)
式中:μ为润滑油黏度;ω为角速度;U为轴颈旋转速度。
1.3 气穴状态下含气率与黏度和密度模型
在气穴状态下,润滑油的黏度和密度随含气率的变化而变化,为了探究其变化规律,文中选用的是实验归纳模型。参考文献[14],对32号汽轮机油充入氮气形成气油两相流,再通过旋转黏度计得到黏度值。
润滑油在较低含气率下黏度变化公式:
μ=μ0(1+αβ2)
(6)
式中:α为常数;β为含气率;μ0为初始黏度;μ为变化后的黏度。
润滑油在常压下密度随含气率的变化公式:
ρ=ρ0(1-bβ)
(7)
式中:b为常数;ρ0为初始密度;ρ为变化后的密度。
1.4 考虑气穴状态下的数学模型建立
在普通滑动轴承Reynolds方程中引入黏度和密度模型。
引入量纲一化参数:
得到量纲一化Reynolds方程:
(8)
1.5 轴颈与轴瓦引入随机圆度误差数学模型
参考文献[15],根据圆度误差的产生原理(即圆度误差为回转体同一横截面被测实际圆对理想圆的变动量),并依据数理统计模型,即基于6Sigma质量管理体系中质量特性值要求,引入Gauss分布的统计学分析模型。并运用Sommerfeld Number对模型进行判定。在满足滑动轴承系统稳定性的前提下,将圆度等级值Y划分为0~12共13级,其中Y=0表示普通滑动轴承轴颈与轴瓦均不存在圆度误差。圆度误差随着圆度误差等级值的增大而增大。
根据文献[16]的规定,圆度误差为宏观误差,波长L和峰值Ha的比值为L/Ha>1 000。根据不同的误差值er,布置不同的点数n,整个圆度上存在的最大波的个数为:n=L/Ha=2πr/er,且点相对于圆周的分布方式为均布方式。根据圆度误差分布的正态性,所以点的大小可用Gauss分布进行确定。点的大小根据6σ进行确定,大小超过6σ区间的概率为0.002 7,不超出的概率为0.997 3,保证了数据的可靠性。
令6σ=er,则μ=er/2,σ=er/6,在MATLAB中利用Gauss分布Δh=normrnd(er/2,er/6,[1,n])。
1.5.1 轴颈引入圆度误差模型
图2所示为轴颈引入圆度误差模型图,Ob为轴瓦圆心,Oj为轴颈圆心,并建立坐标轴,得到油膜厚度表达式:
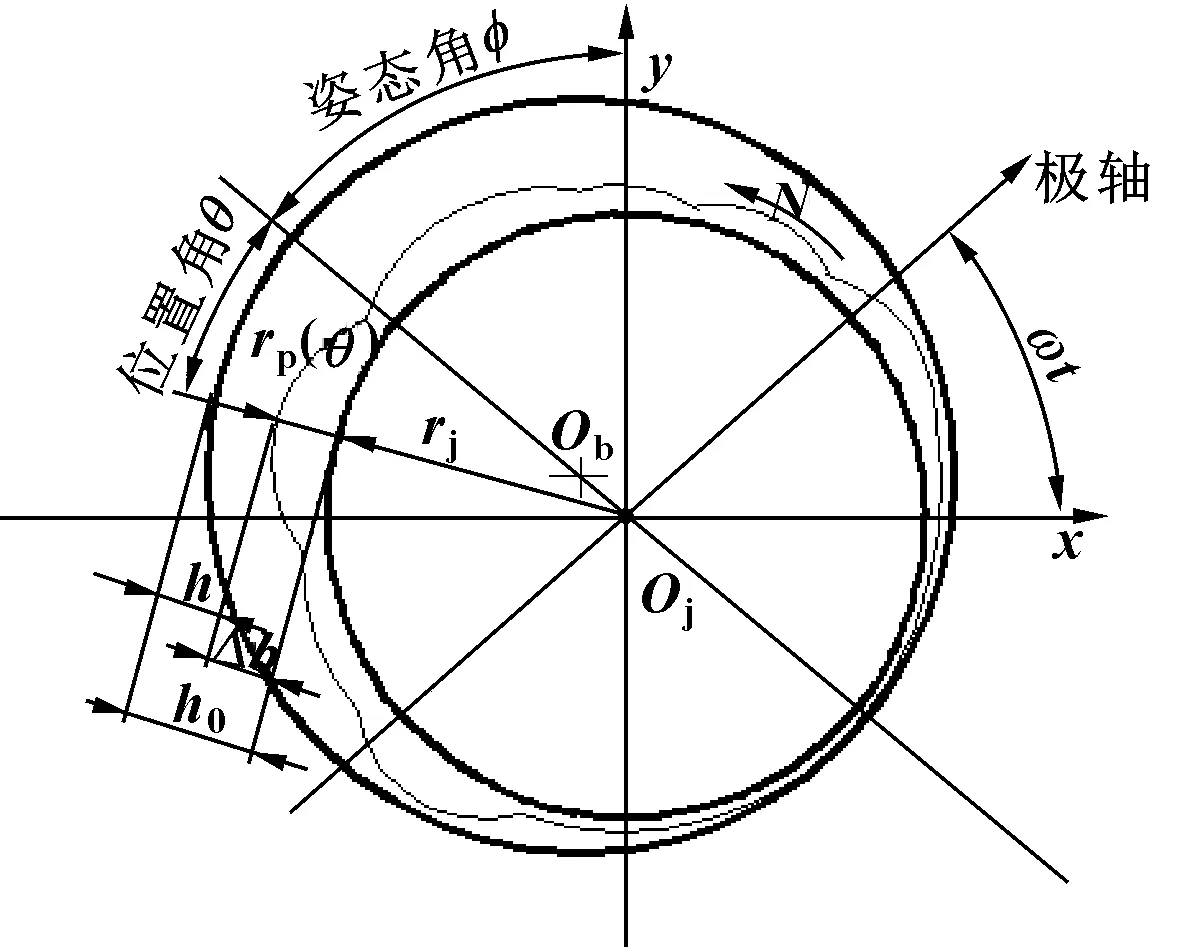
图2 轴颈圆度误差模型
h=h0-Δh
(9)
式中:h0表示普通油膜厚度;Δh表示误差值的大小。
(10)
(11)
Δh=rp(θ)-rj
(12)
(13)
c/rj值相对较小可忽略,上式化简为
h≈c(1+εcosθ)-rp(θ)+rj
(14)
式中:rj为轴颈半径;rp(θ)为引入轴颈圆度误差的轴颈半径。
1.5.2 轴瓦引入圆度误差模型
图3所示为轴瓦引入圆度误差模型图,Ob为轴瓦圆心,Oj为轴颈圆心,并建立坐标轴,得到油膜厚度表达式:
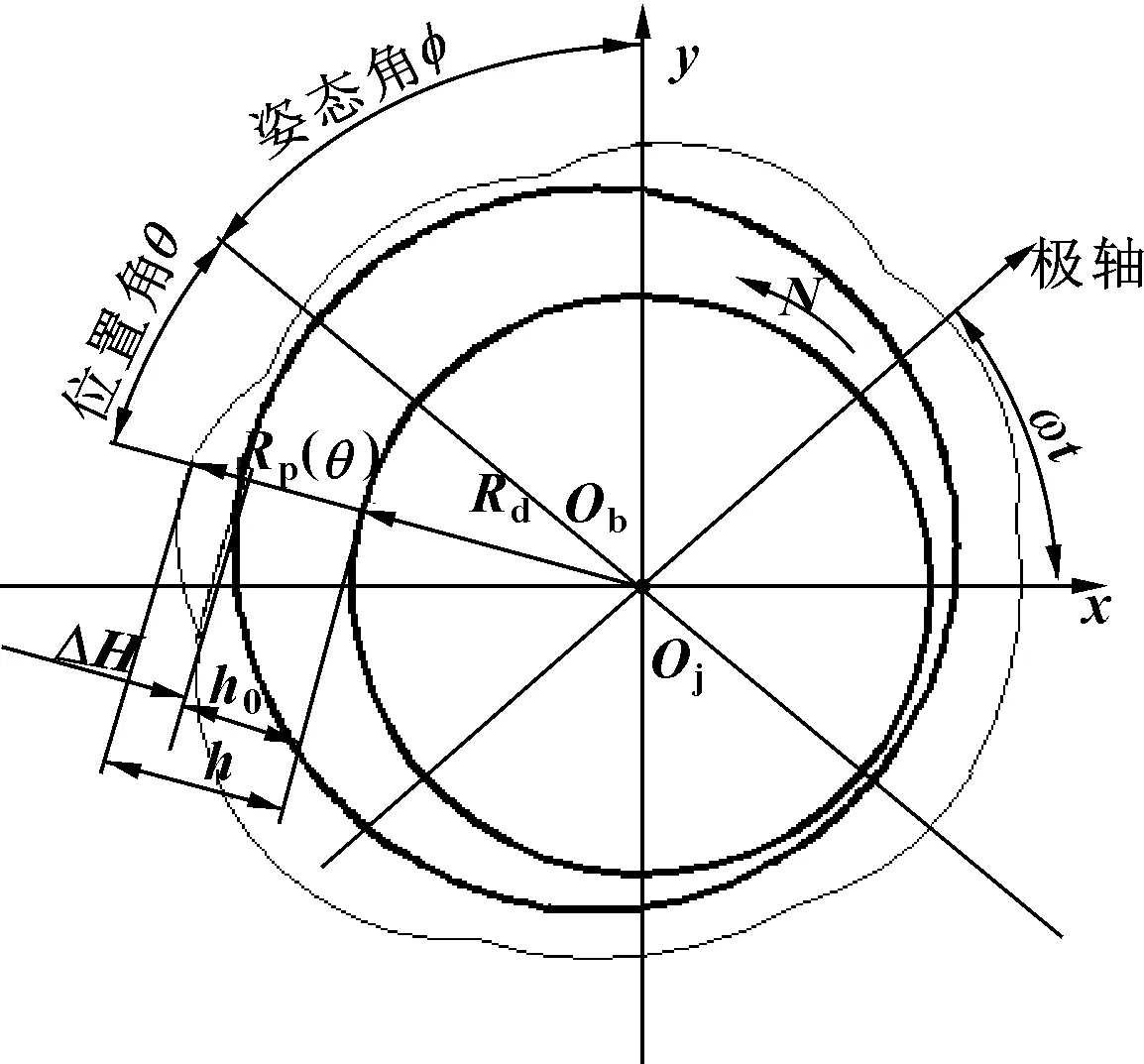
图3 轴瓦圆度误差油膜模型
h=h0+ΔH
(15)
式中:h0表示普通油膜厚度;ΔH表示误差值的大小。
(16)
(17)
ΔH=Rp(θ)-Rd
(18)
Rp(θ)-Rd(θ)
(19)
h≈c(1+εcosθ)+Rp(θ)-Rd
(20)
式中:Rd为轴颈半径;Rp(θ)为轴瓦引入圆度误差的轴瓦半径。
1.6 引入轴颈和轴瓦圆度误差数学模型
在普通滑动轴承Reynolds方程中引入轴颈和轴瓦的圆度误差。并引入量纲一化参数得到量纲一化Reynolds方程
H(φ,λ)=h(x,z)/c
(21)
(22)
1.7 同时考虑气穴和圆度误差的雷诺方程
同时考虑气穴和随机圆度误差时,需要将润滑油的密度和黏度变化考虑进去,且同时考虑随机圆度误差对油膜厚度变化的影响,参考文献[17]在气穴状态下,油膜厚度对其流变特性无影响。所以可将引入圆度误差和气穴的Reynolds方程耦合得到考虑气穴和圆度误差的耦合Reynolds方程。
(23)
2 耦合方程的数值求解
2.1 静特性参数求解
油膜量纲一承载力W的垂直分力Wy和水平分力Wx的表达式为
(24)
(25)
量纲一油膜承载力W的计算公式为
(26)
油膜量纲一端泄流量的计算公式为
(27)
油膜摩擦功耗的计算公式为
(28)
2.2 边界条件
引入雷诺边界条件,其一维和二维的表达式分别为:p=pa,∂p/∂x=0;p=pa,∂p/∂x=∂p/∂z=0。
式中:pa为气穴压力,取大气压力pa=0。
2.3 求解流程
利用有限差分法求解油膜压力和静特性参数,流程图如图4所示。

图4 计算流程

3 结果与分析
3.1 理论模型验证
为了验证所建数学模型的正确性,文中结合文献[7]对不同转速下偏心率下的承载力,进行了仿真计算,并将所得结果与实验数据对比分析。表1给出了滑动轴承和润滑油的主要参数。

表1 滑动轴承主要参数
图5所示为文中拟合及文献[7]实验得到的滑动轴承承载力在1 000~5 000 r/min轴颈转速范围内的变化情况。可见,文献[7]实验结果与拟合结果之间的相对误差仅为1.5%~4.6%。通过对比验证了所建数学模型的正确性,可进一步研究综合考虑气穴和圆度误差因素对轴承润滑静特性的影响。
3.2 气穴和圆度误差因素对滑动轴承静特性的影响
3.2.1 同时考虑气穴和轴颈圆度误差因素分析
图6所示为润滑油不同含气率和轴颈不同圆度误差下量纲一最大油膜压力分布。图7所示为润滑油不同含气率和轴颈不同圆度误差下量纲一承载力随偏心率的变化关系。
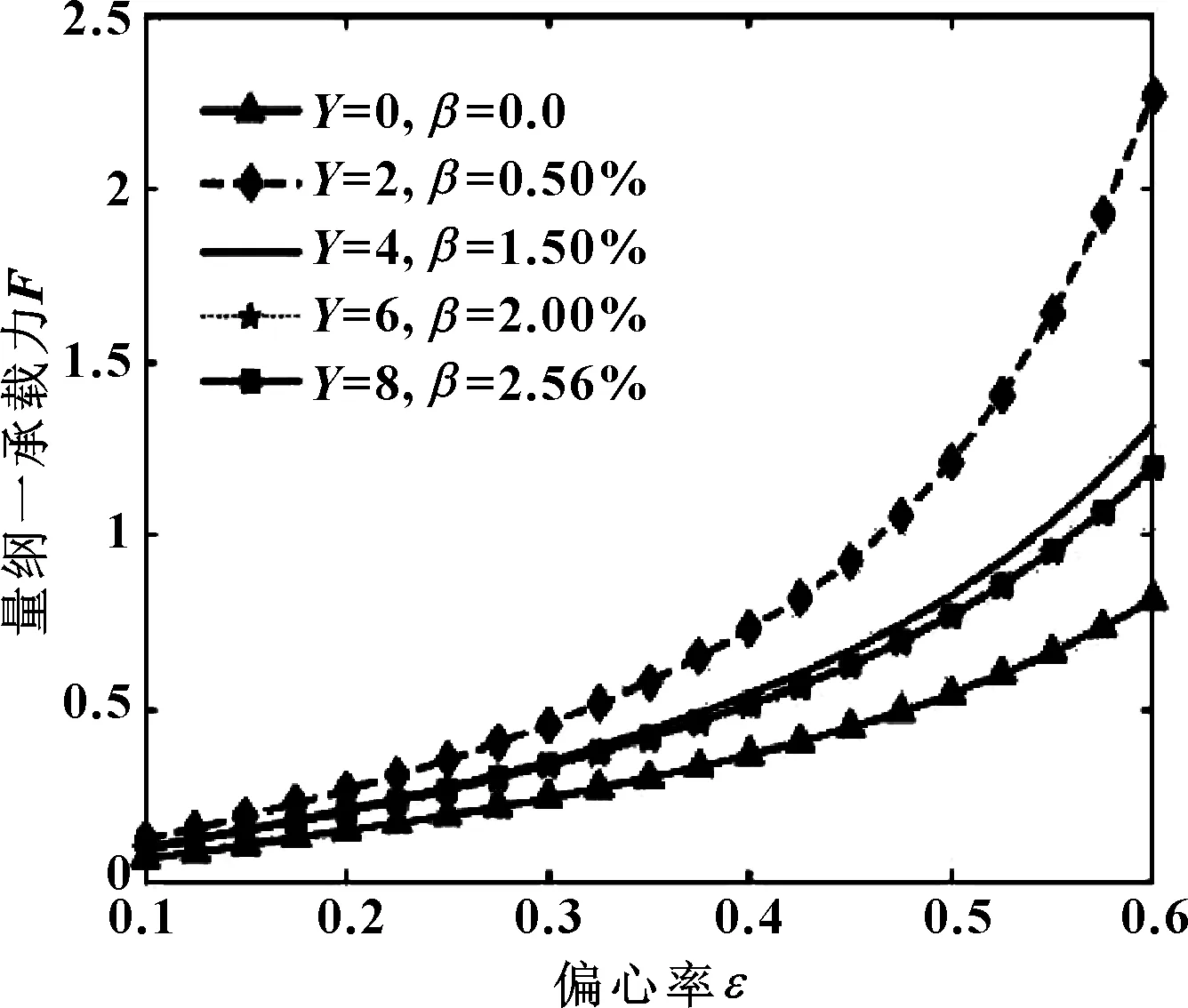
图7 不同含气率和轴颈圆度误差下量纲一承载力随偏心率的变化
由图6、7可知,当偏心率较小时,圆度误差和含气率影响较小,曲线之间无明显区分;当偏心率为最大值时,圆度误差和含气率影响达到最大;量纲一最大油膜压力和承载力随着轴颈圆度误差和润滑油含气率值的增大而减小,且两者始终大于未考虑圆度误差和含气率的情况。
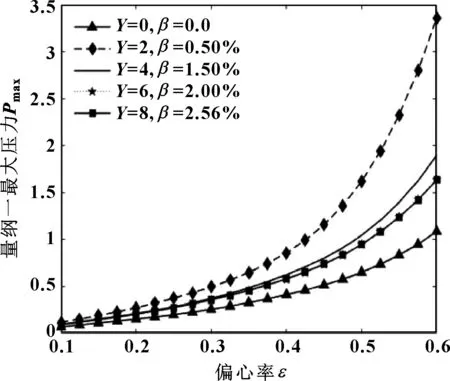
图6 不同含气率和轴颈圆度误差下量纲一
图8所示为润滑油不同含气率和轴颈不同圆度误差下量纲一端泄流量随偏心率的变化关系。图9所示为润滑油不同含气率和轴颈不同圆度误差下摩擦功耗随偏心率变化关系。
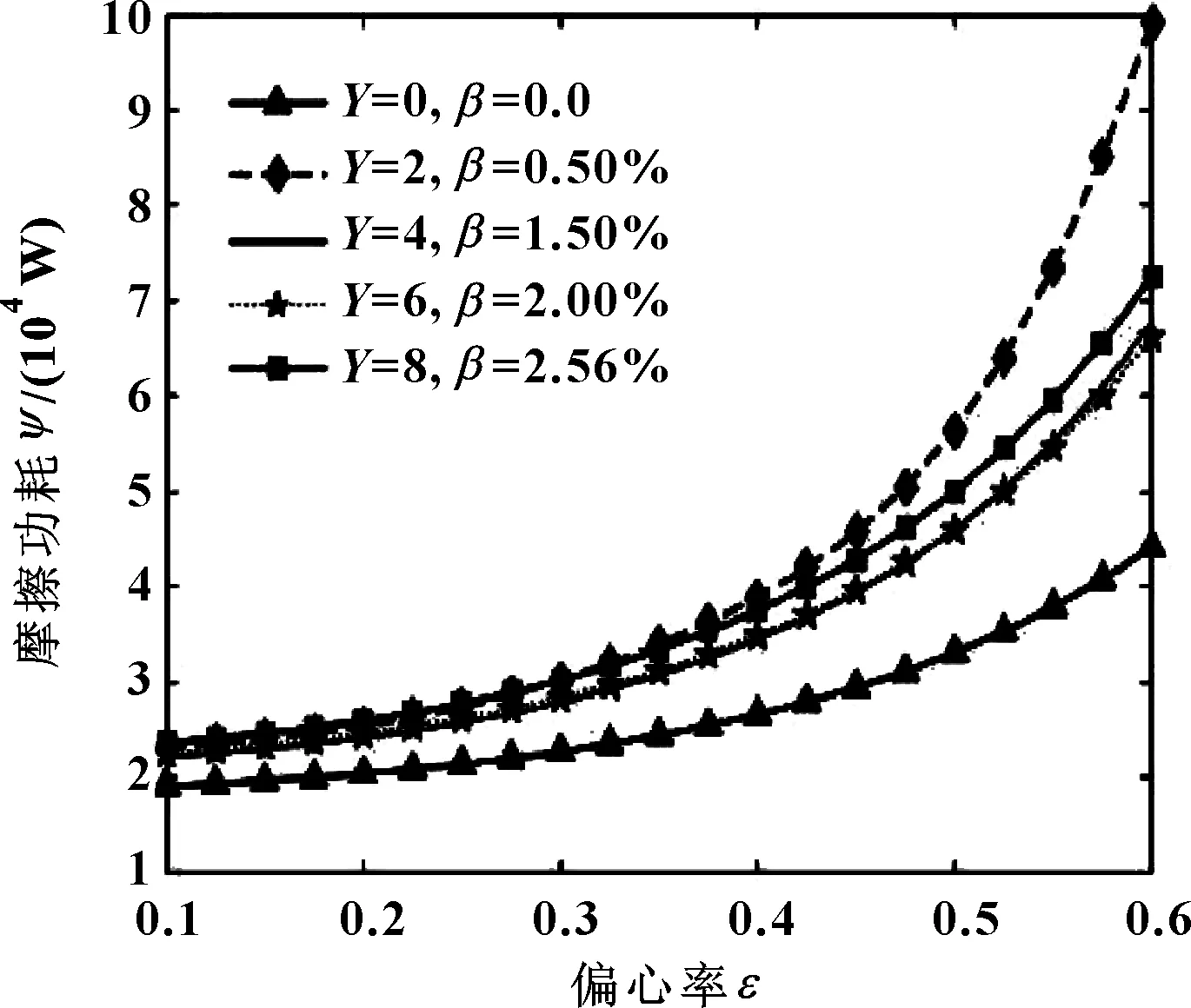
图9 不同含气率和轴颈圆度误差下摩擦功耗随偏心率的变化
由图8、9可知,在偏心率较小时,圆度误差和含气率影响较小;当偏心率为最大值时,圆度误差和含气率影响达到最大;量纲一端泄流量随着圆度误差和含气率的增加而增加,但变化曲线之间区分不明显;摩擦功耗随着圆度误差和含气率的增加先增加后减小,且量纲一端泄流量和摩擦功耗始终大于未考虑圆度误差和含气率的情况。
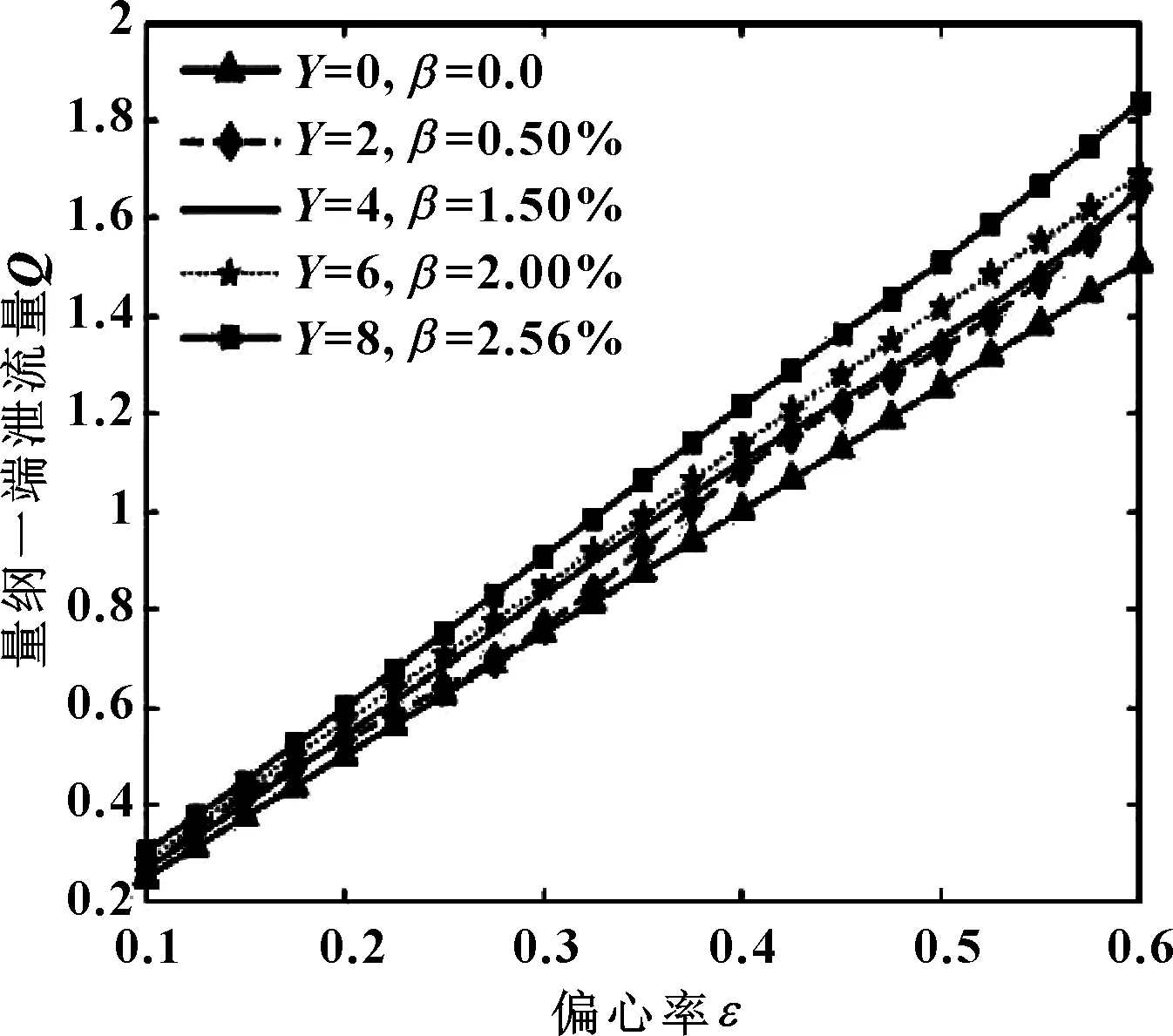
图8 不同含气率和轴颈圆度误差下量纲一端泄流量随偏心率的变化
3.2.2 同时考虑气穴和轴瓦圆度误差因素分析
图10所示为润滑油不同含气率和轴瓦不同圆度误差下量纲一最大油膜压力随偏心率变化关系。图11所示为润滑油不同含气率和轴瓦不同圆度误差下量纲一承载力随偏心率的变化关系。
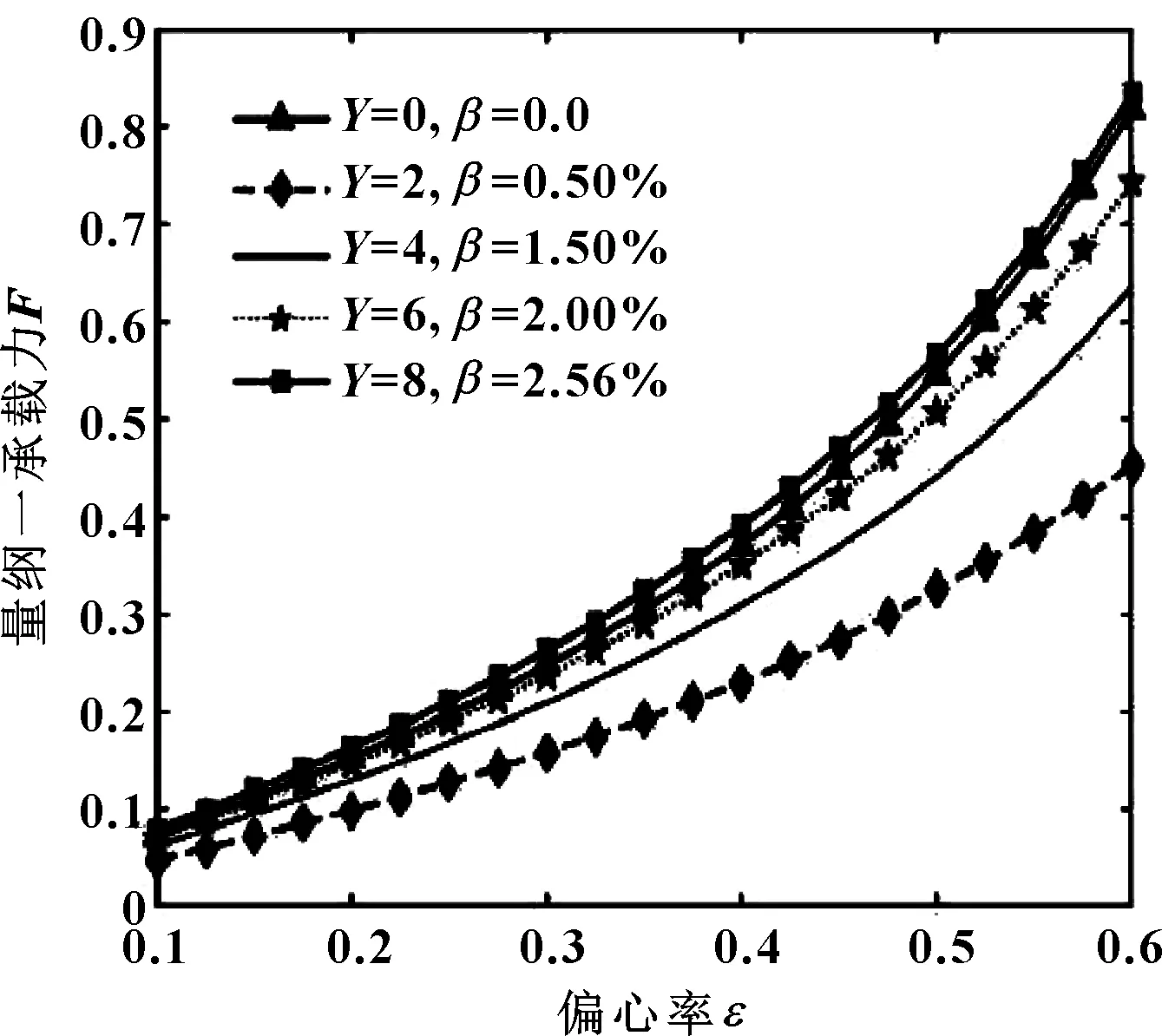
图11 不同含气率和轴瓦圆度误差下量纲一承载力随偏心率的变化
由图10、11可知,在偏心率较小时,圆度误差和含气率影响较小,曲线之间无明显区分;当偏心率最大时,圆度误差和含气率影响达到最大;量纲一最大油膜压力和承载力开始小于未考虑圆度误差和含气率的情况,并且随着轴颈圆度误差和润滑油含气率值的增加而增加。
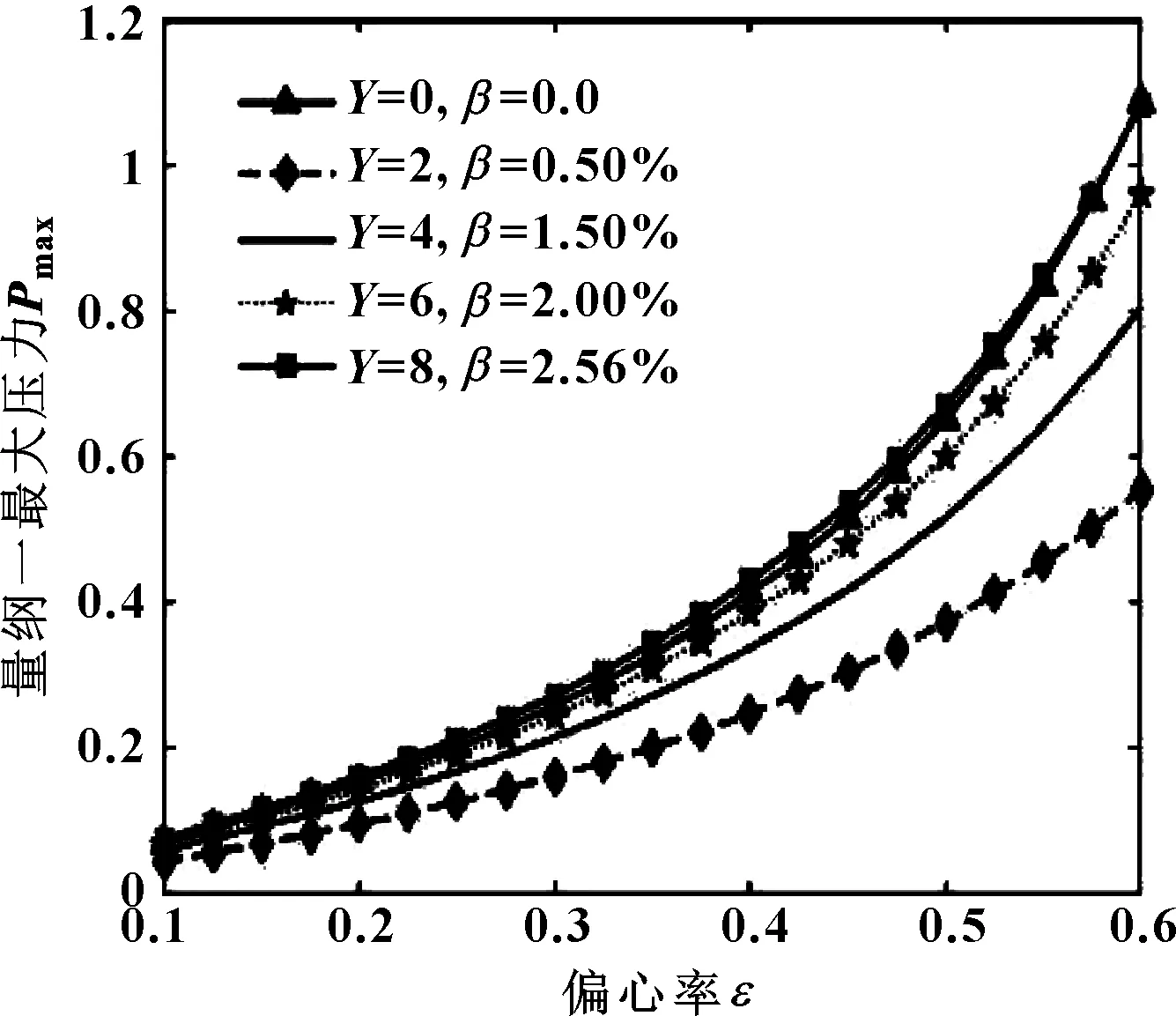
图10 不同含气率和轴瓦圆度误差下量纲一最大油膜压力随偏心率的变化
图12、13所示为润滑油不同含气率和轴瓦不同圆度误差下量纲一端泄流量和摩擦功耗随偏心率的变化关系。
由图12、13可得,在偏心率较小时,圆度误差和含气率影响较小;当偏心率最大时,含气率和圆度误差影响达到最大;量纲一端泄流量随着圆度误差和含气率的增加而增加,但变化曲线之间区分不明显;摩擦功耗随着圆度误差和含气率的增加而增长;且量纲一端泄流量始终大于未考虑圆度误差和含气率的情况,摩擦功耗开始小于未考虑圆度误差和含气率的情况,并且随着轴瓦圆度误差和润滑油含气率值的增加而增加。
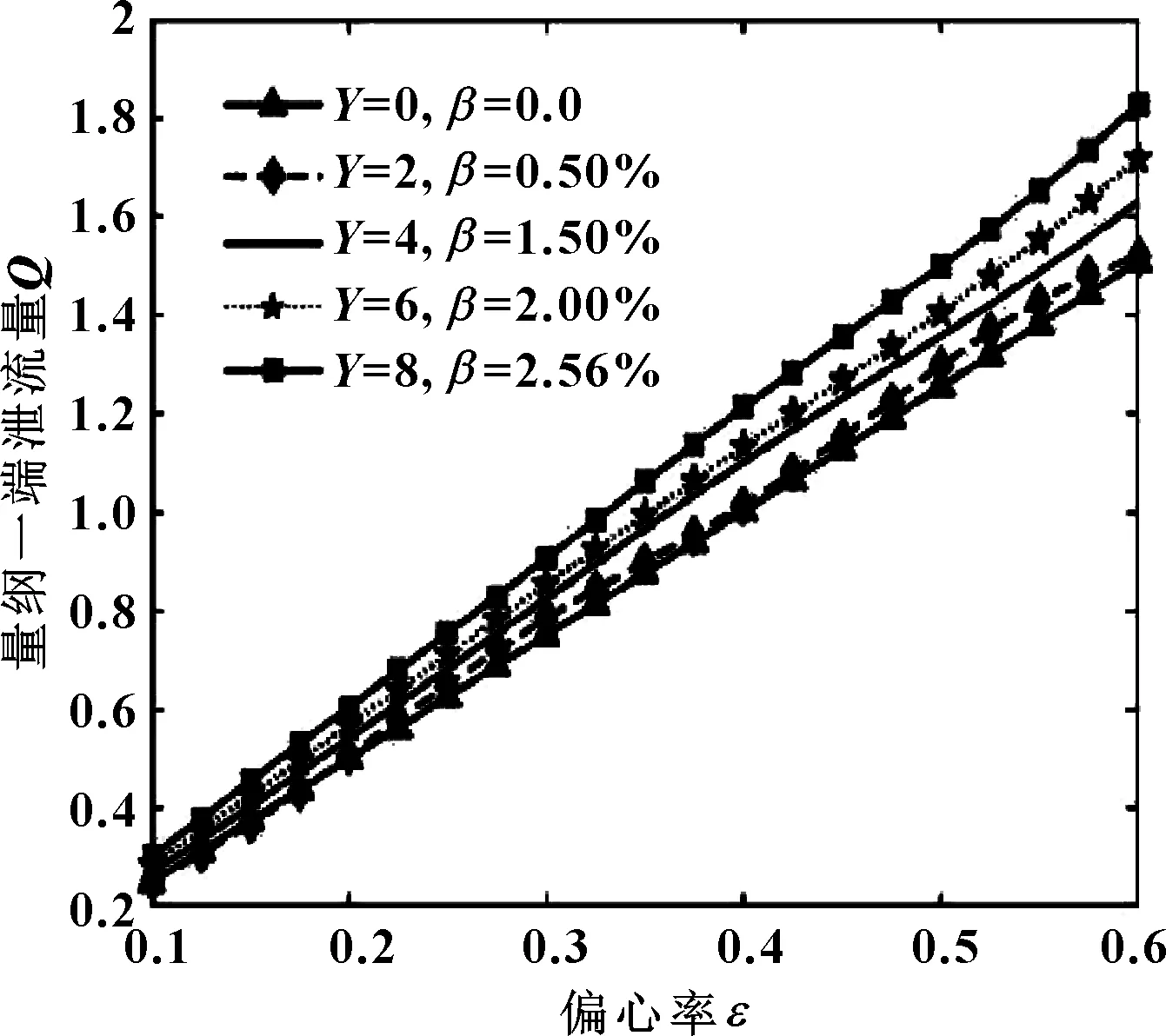
图12 不同含气率和轴瓦圆度误差下量纲一端泄流量随偏心率的变化

图13 同含气率和轴瓦圆度误差下摩擦功耗随偏心率的变化
3.3 气穴因素对滑动轴承静特性的影响
图14所示为不同偏心率下量纲一最大油膜压力随含气率变化关系。

图14 不同偏心率下量纲一最大油膜压力随含气率的变化
由图14可知,当偏心率较小时最大油膜压力受影响较小,且润滑油受不同含气率值的影响也不明显;当偏心率较大时,最大油膜压力受影响较大,且随着含气率的增加而增加。
图15所示为不同偏心率下量纲一承载力随润滑油含气率变化关系。可知,偏心率较小时,量纲一承载力受影响较小,且润滑油不同含气率对承载力影响也不明显;偏心率较大时,量纲一承载力受影响较大,且随着润滑油含气率的增加而增加。
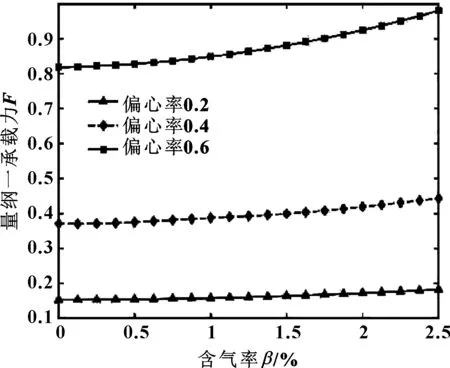
图15 不同偏心率下量纲一承载力随含气率的变化
图16所示为不同偏心率下量纲一端泄流量随含气率变化关系。可得,当偏心率较小时量纲一端泄流量受影响较小,且端泄流量随着含气率值的增加而增加;当偏心率较大时,量纲一承载力受影响较大,且随着含气率的增加而增大。

图16 不同偏心率下量纲一端泄流量随含气率的变化
图17所示为摩擦功耗随含气率变化关系。可知,小偏心率下,量纲一端泄流量受其影响较小,且随着含气率值的增加而增大;偏心率较大时,对摩擦功耗影响较大,且随着润滑油含气率的增加而增加。
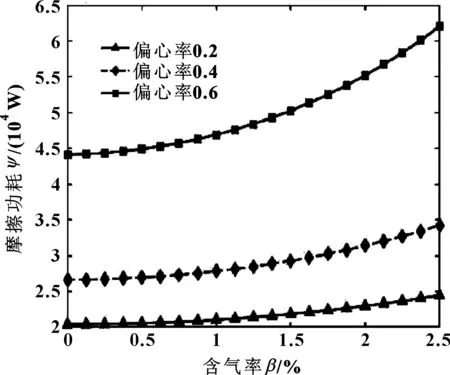
图17 不同偏心率下摩擦功耗随含气率的变化
3.4 圆度误差因素对滑动轴承静特性的影响
图18、图19所示为不同偏心率下量纲一最大油膜压力随圆度误差等级变化关系。可知,对于轴颈和轴瓦而言,偏心率较小时,圆度误差等级对量纲一最大油膜压力影响不明显;偏心率较大时,量纲一最大油膜压力随着轴颈圆度误差等级的增加而减小,随轴瓦圆度误差等级的增加而增加。
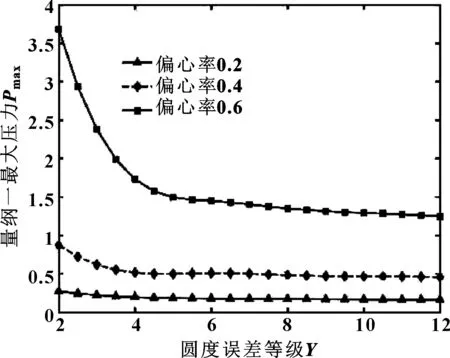
图18 不同偏心率下量纲一最大油膜压力随轴颈圆度误差的变化
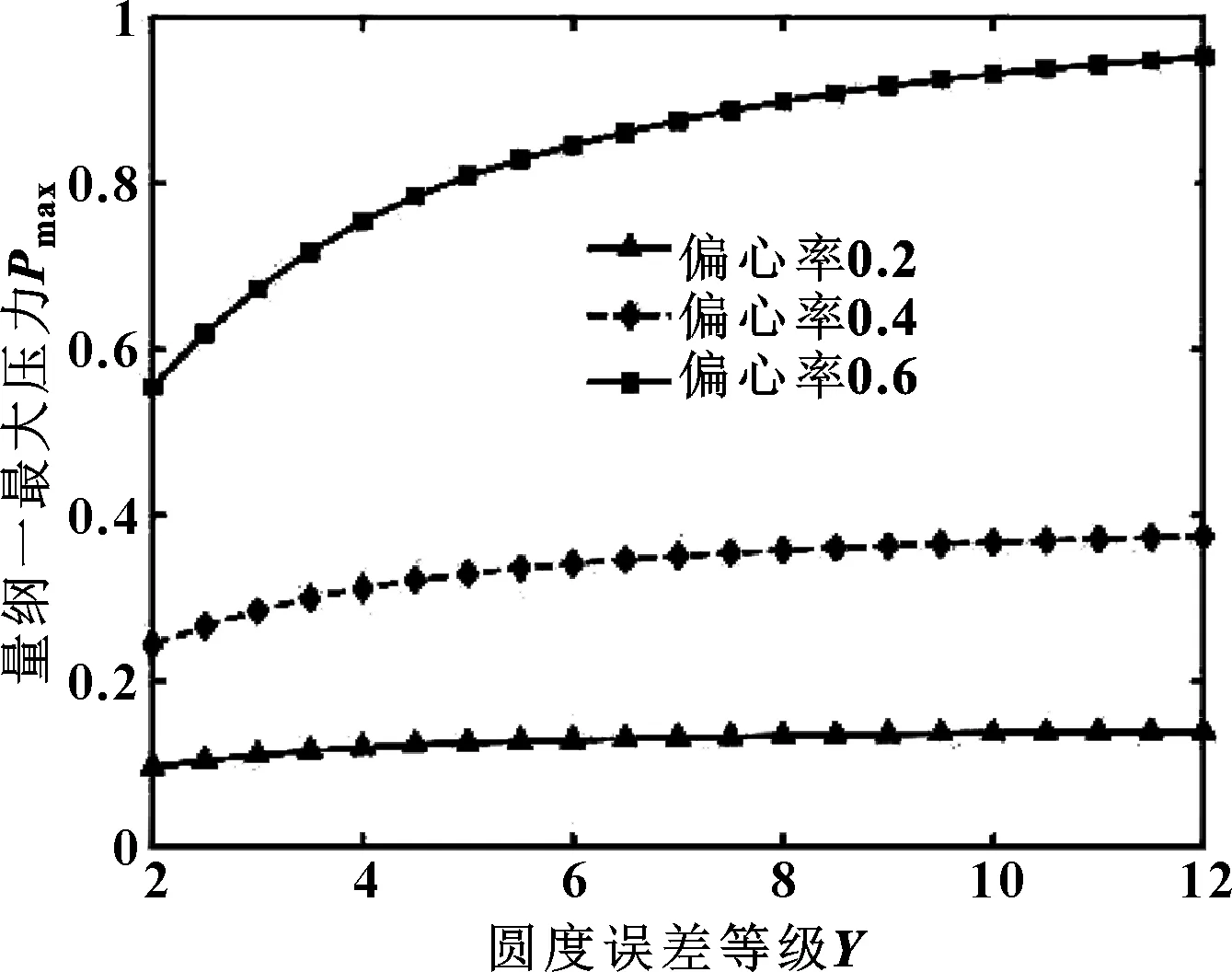
图19 不同偏心率下量纲一最大油膜压力随轴瓦圆度误差的变化
图20所示为量纲一承载力随轴颈圆度误差等级变化关系。图21所示为量纲一承载力随轴瓦圆度误差等级变化曲线。可得,当偏心率值较小,轴颈和轴瓦圆度误差等级对量纲一承载力影响不明显;偏心率较大时,量纲一承载力随着轴颈圆度误差等级的增加而减小,随轴瓦圆度误差等级的增加而增大。
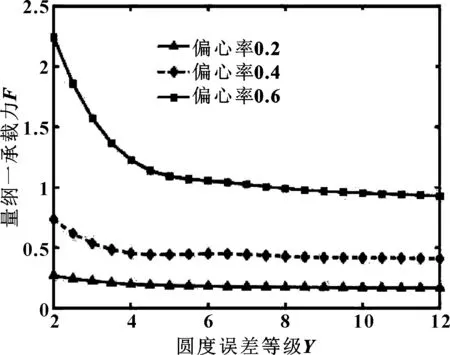
图20 不同偏心率下量纲一承载力随轴颈圆度误差的变化
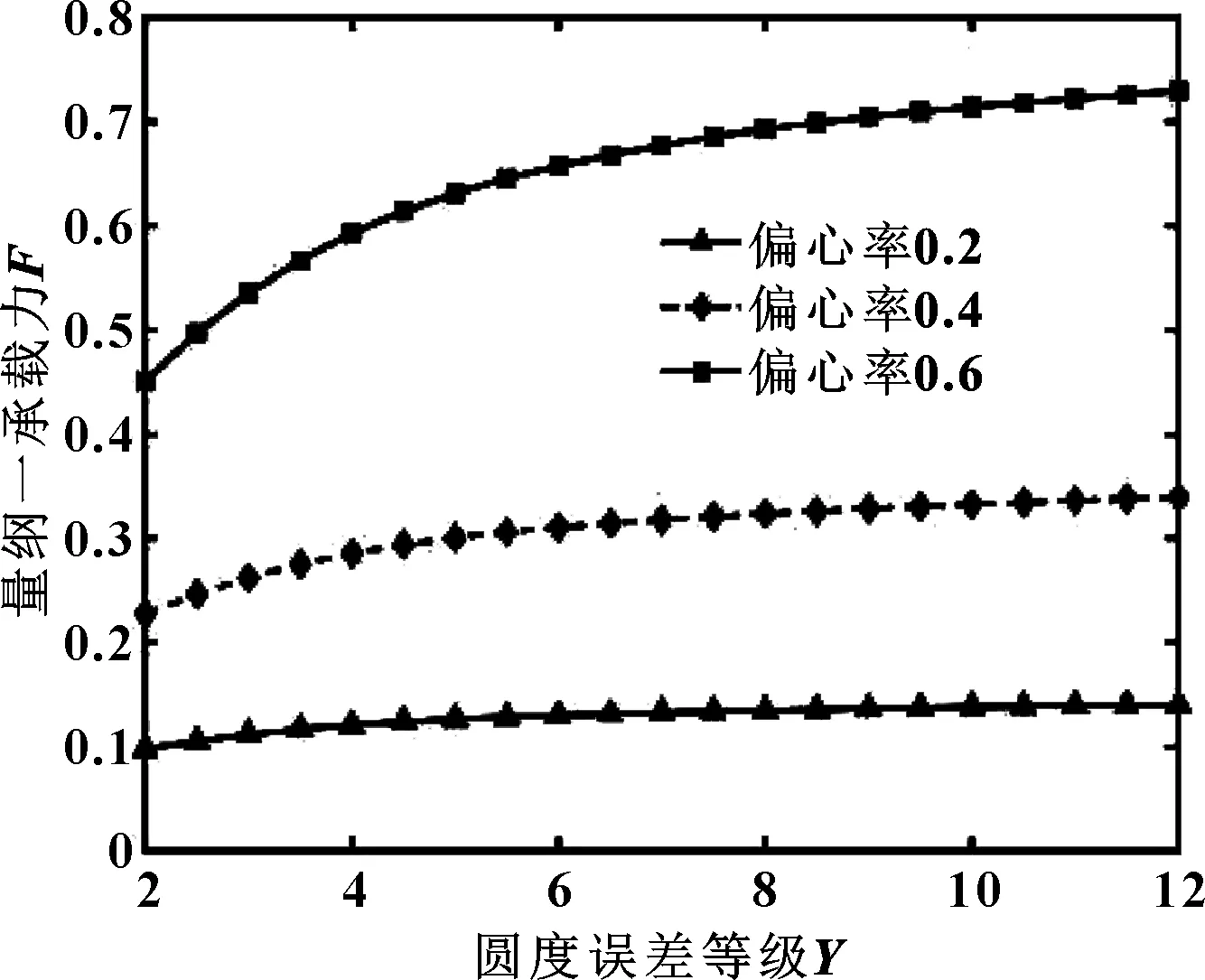
图21 不同偏心率下量纲一承载力随轴瓦圆度误差的变化
图22、23所示为量纲一端泄流量随圆度误差等级变化关系。可知,对于轴颈和轴瓦而言,量纲一端泄流量随着偏心率的增大而增大,但受圆度误差等级的影响不明显。
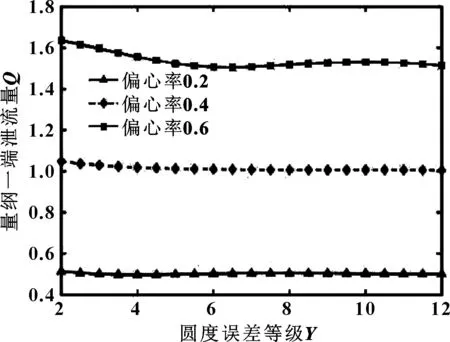
图22 不同偏心率下量纲一端泄流量随轴颈圆度误差的变化
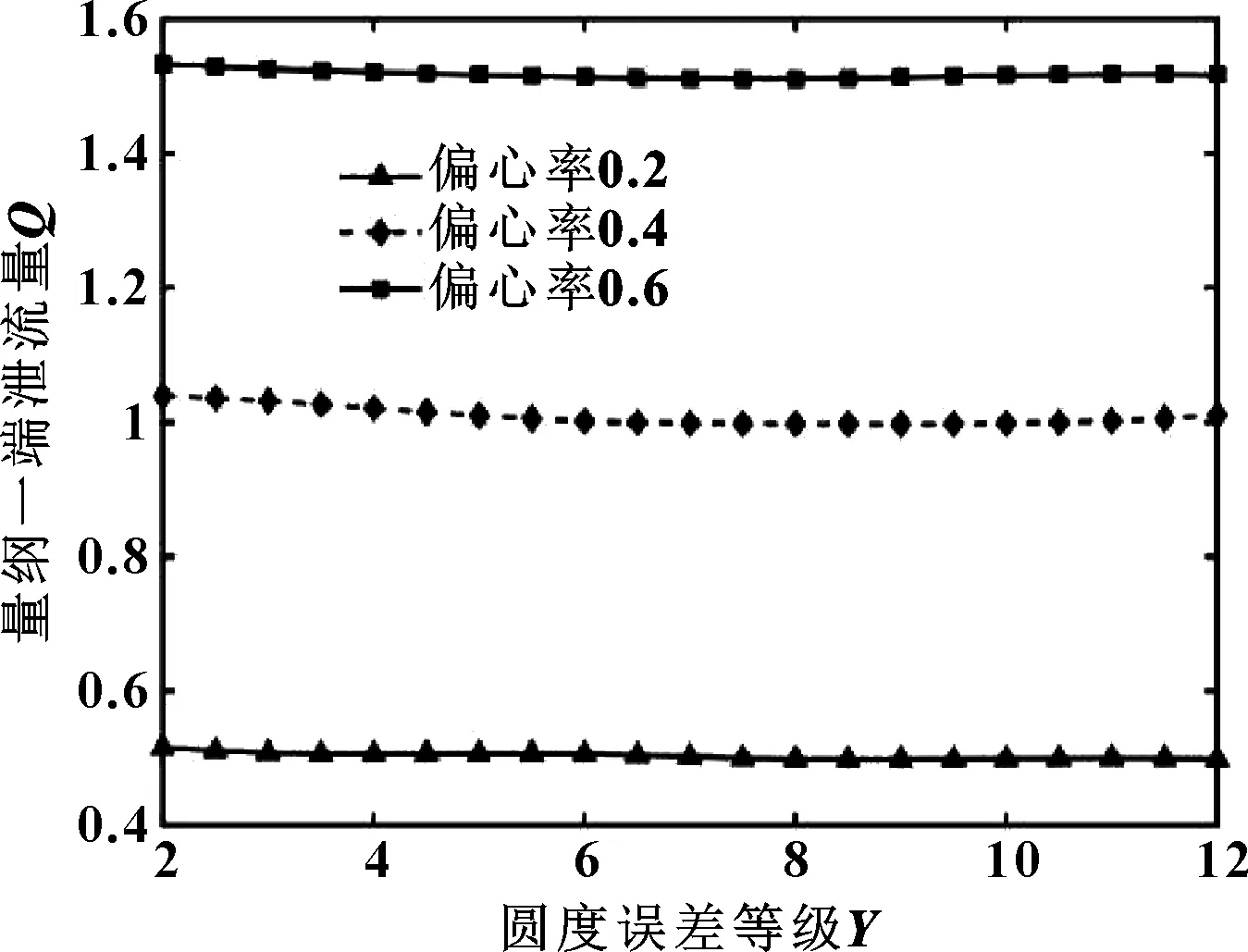
图23 不同偏心率下量纲一端泄流量随轴瓦圆度误差的变化
图24、25所示为摩擦功耗随圆度误差等级变化关系。可知,对于轴颈和轴瓦而言,偏心率较小时,圆度误差等级对摩擦功耗影响不明显;偏心率较大时,摩擦功耗随着轴颈圆度误差等级的增加而减小,随轴瓦圆度误差等级的增加而增加。
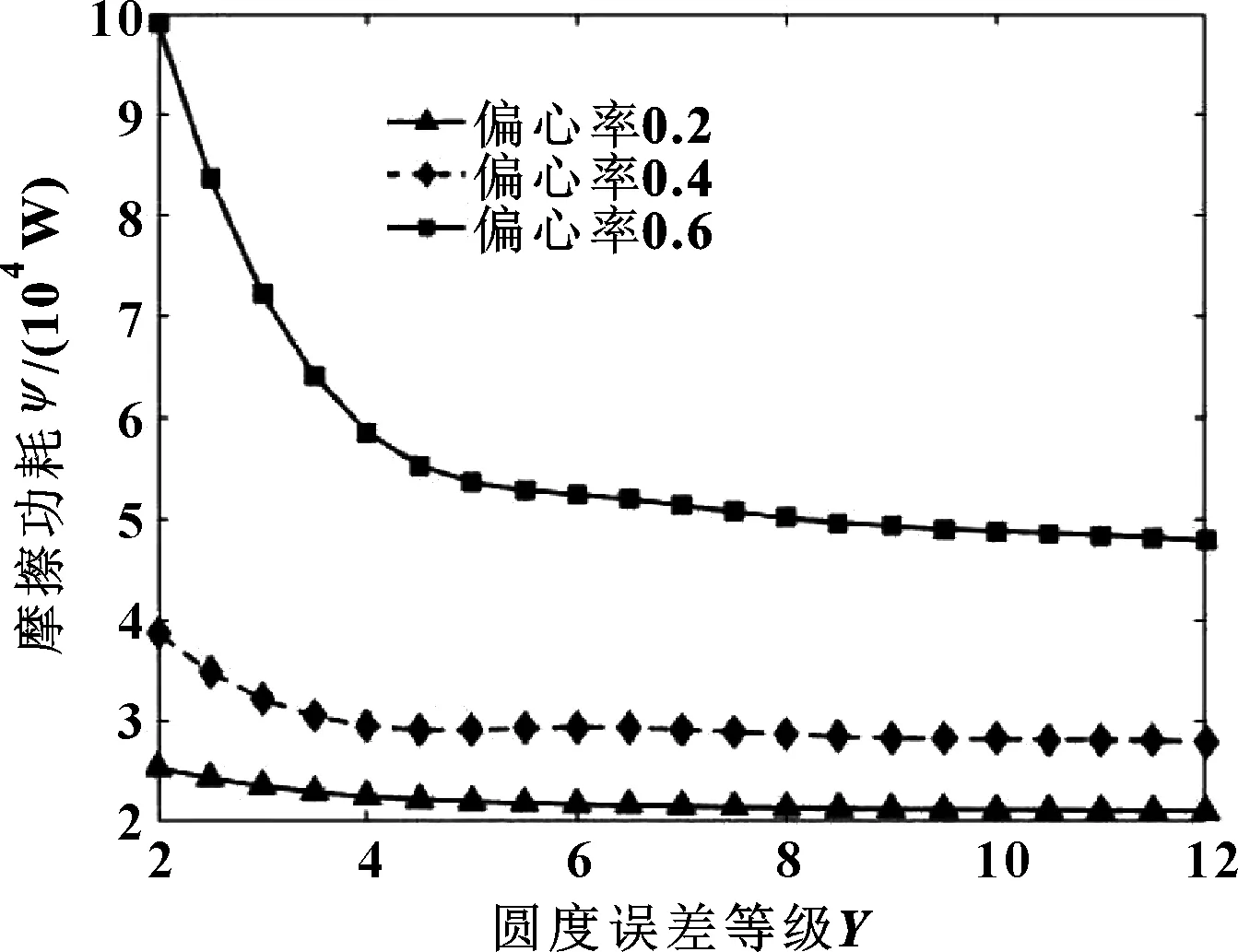
图24 不同偏心率下摩擦功耗随轴颈圆度误差的变化
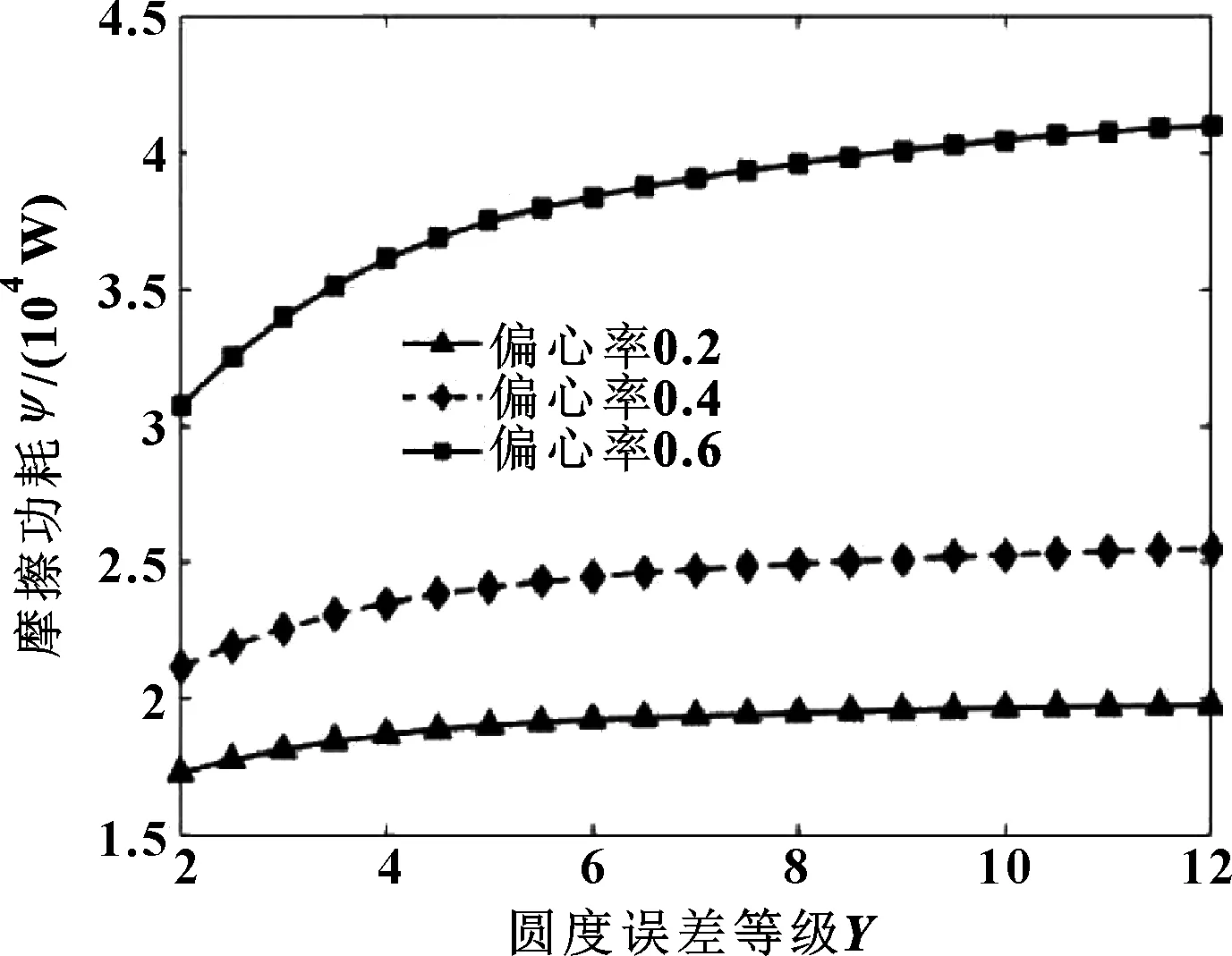
图25 不同偏心率下摩擦功耗随轴瓦圆度误差的变化
4 结论
针对特定结构尺寸的动压径向滑动轴承,根据轴承结构特点选用适合的求解方法,计算得到不同工况下滑动轴承静特性参数。对比单独考虑气穴、轴颈和轴瓦圆度误差因素的情况有以下结论:
(1)对于量纲一最大油膜压力和承载力而言,圆度误差的影响大于气穴的影响;
(2)对于量纲一端泄流量而言,气穴的影响大于圆度误差等级的影响,圆度误差等级几乎毫无影响;
(3)对于摩擦功耗而言,小偏心率情况下圆度误差等级的影响较大,大偏心率情况下,气穴的影响大于圆度误差等级的影响;
(4)气穴使最大油膜压力、端泄流量、承载力和摩擦功耗增长;圆度误差对油膜压力、承载力、摩擦功耗等静态参数影响较大,对端泄流量几乎毫无影响。
——以匀加速直线运动公式为例

