结构化凹坑减阻表面的拓扑磨削与仿真研究*
齐永超 吕玉山 李兴山 许刘宛 衣军任
(沈阳理工大学机械工程学院 辽宁沈阳 110159)
本文作者针对凹坑结构化表面,提出拓扑磨削的加工方法,依据工件的结构化表面特征设计结构化砂轮,建立磨削运动模型,并进行磨削过程仿真研究。
1 结构化表面拓扑特征分析
1.1 结构单元形状拓扑特征分析
研究表明,凹坑型结构化表面上结构单元的形状尺寸和排布影响着减阻减磨性能[11-12]。土壤动物蜣螂头部和上唇基分布有圆形及椭圆形的凹坑,具有很好的减黏降阻作用[13]。文中即以椭球冠及球冠形凹坑为例,建立公式(1)所示的结构单元数学模型。
(1)
式中:n=h/c,c为椭球冠所在椭圆z轴半径;l、w、h分别为结构单元长度、宽度和深度。
当l>w时,结构单元形状为椭球冠形,当l=w时,结构单元形状为球冠形。图1为结构单元模型图。
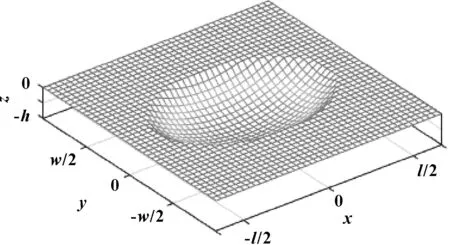
图1 凹坑结构单元模型
由数学模型(1)可知,参数l、w、h决定结构单元的尺寸形状,由此提取其为拓扑特征参量,建立结构单元拓扑特征矩阵为
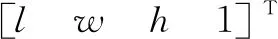
(2)
1.2 结构单元排布拓扑特征分析
依据生物表面结构单元排布方式,建立阵列、错位、叶序3种排布规律的数学模型,图2为单元排布示意图。定义单元长度所在的工件与砂轮相对运动方向为工件固定坐标系xw轴方向,宽度方向为yw轴方向,垂直工件表面方向为zw轴方向,被磨削平面为zw=0平面。xw方向排布Iw列,yw方向排布Jw行。则阵列排布数学表达式:
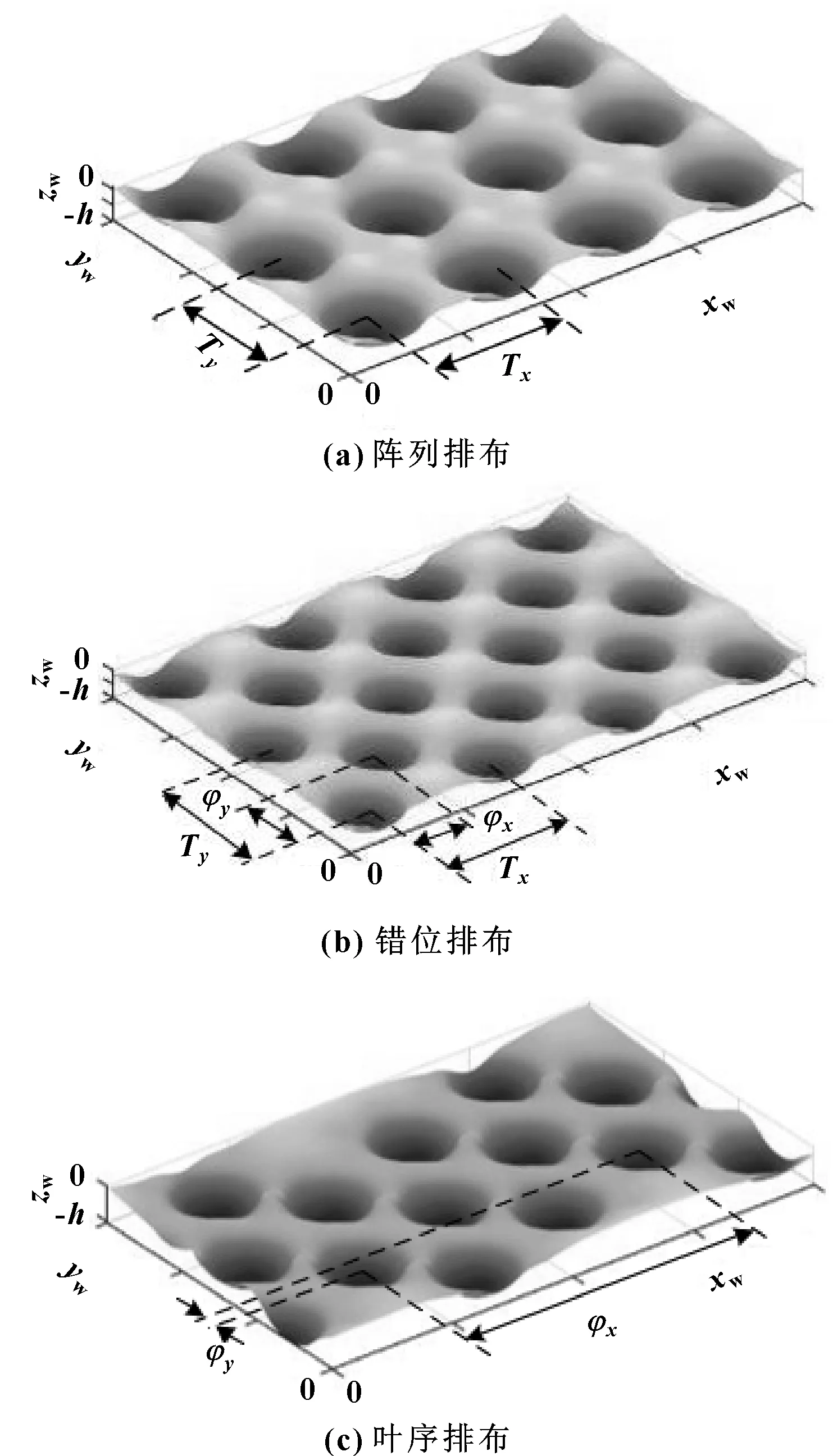
图2 结构单元排布模型
(3)
错位排布数学表达式为
(4)
式中:i=1,2,3,......,Iw;j=1,2,3,......,Jw;(xi,yj)为任意结构单元中心点坐标;Tx、Ty分别为xw、yw方向排布周期;φx为xw方向相位差。
叶序排布数学表达式为
(5)
式中:R为Van Iterson模型[14-15]中母体圆柱半径;c为叶序排布生长序数;叶序角θ=137.508°,k=1,2,3,......,Kw,为结构单元序数;m为控制第k个结构单元在xw轴方向上的排布序数;φy为yw方向相位差。
由公式(3)—(5)可知,结构化表面的排布特征由排布周期与相位差决定,阵列排布由排布周期Tx和Ty控制结构单元排布间距,行列之间整齐排列,相位差为0;错位排布xw方向与yw方向排布周期分别为Tx、Ty,偶数行与奇数行之间相位差为φx;叶序排布xw方向有相位差φx,yw方向有相位差φy。则提取3种排布的周期与相位建立特征向量矩阵为
[Twp]=[TxTyφxφy]T
(6)
2 结构化砂轮设计
2.1 凹坑结构化表面创成机制
图3所示为单元长度方向磨粒簇中心截面磨削过程示意图,磨料簇在砂轮周向间隔排布。在工件上弧AB段为磨削阶段,砂轮上A′B′段为磨粒簇与工件接触磨削出的凹坑单元;BC段为空闲阶段,砂轮上B′C′段不磨削工件,在结构单元间形成平台间隔。
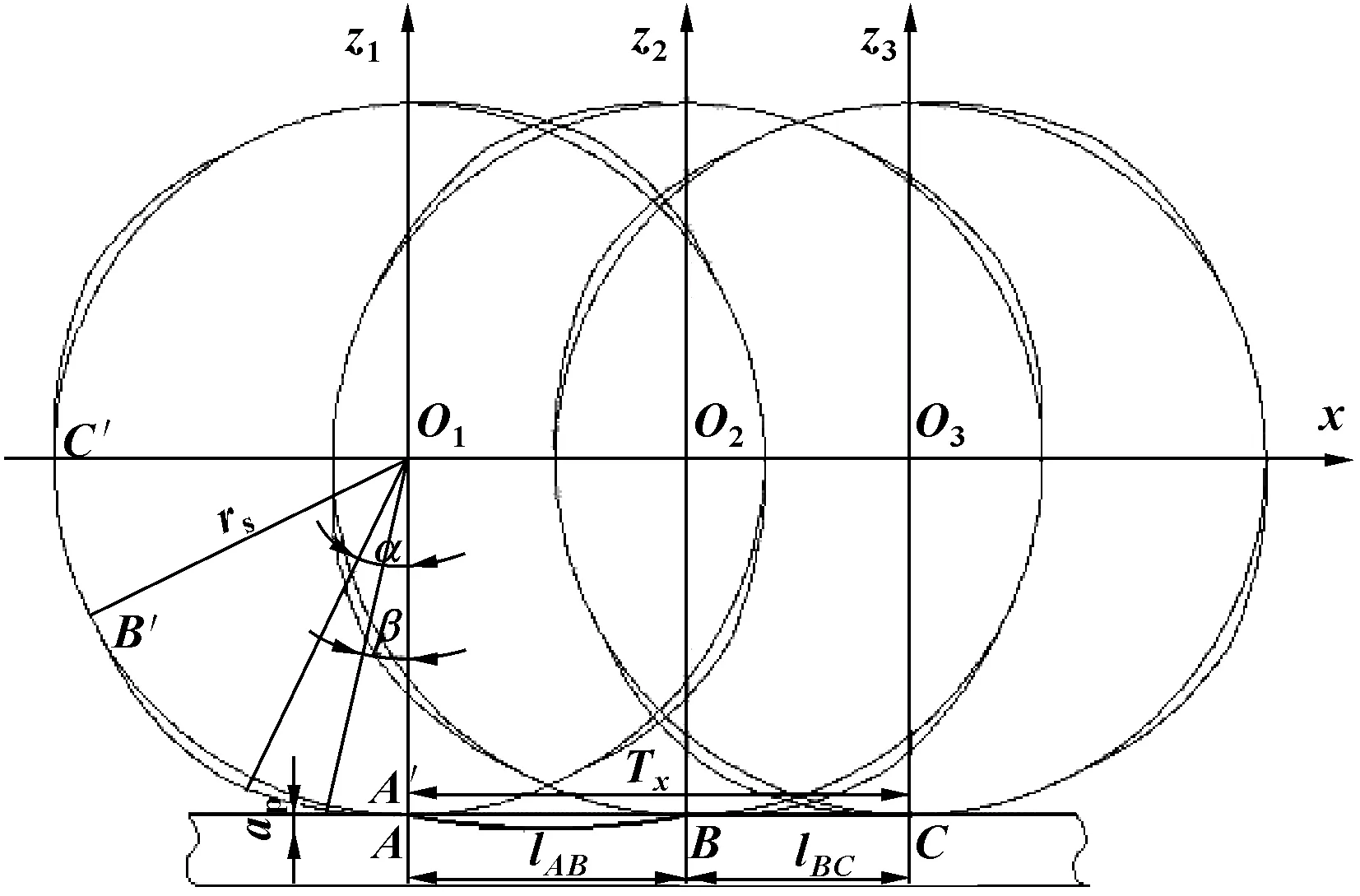
图3 截面磨削过程示意
中心截面各磨粒运动轨迹如图4所示,磨削过程中磨料簇内各个磨粒相对工件做延长外摆线运动,各磨粒运动轨迹在工件表面包络形成结构单元轮廓。磨料簇最低点A′从切入点开始进入磨削阶段,由于磨料簇高度逐渐增大,高点磨粒从切入点左侧开始切削,形成超越切入点的长度l1,且存在某一点磨粒,超越切入点距离最大为l1max。l2为磨料簇与工件接触时长内工件进给的距离,l3为超越切出点长度,与l1相等。设定砂轮磨料簇高度变化为f(α),磨料簇长度为L,最大高度差为H,周向排布间隔φs,砂轮基体半径为rs,平均磨粒直径为dg,磨削深度为ap,则长度l1为
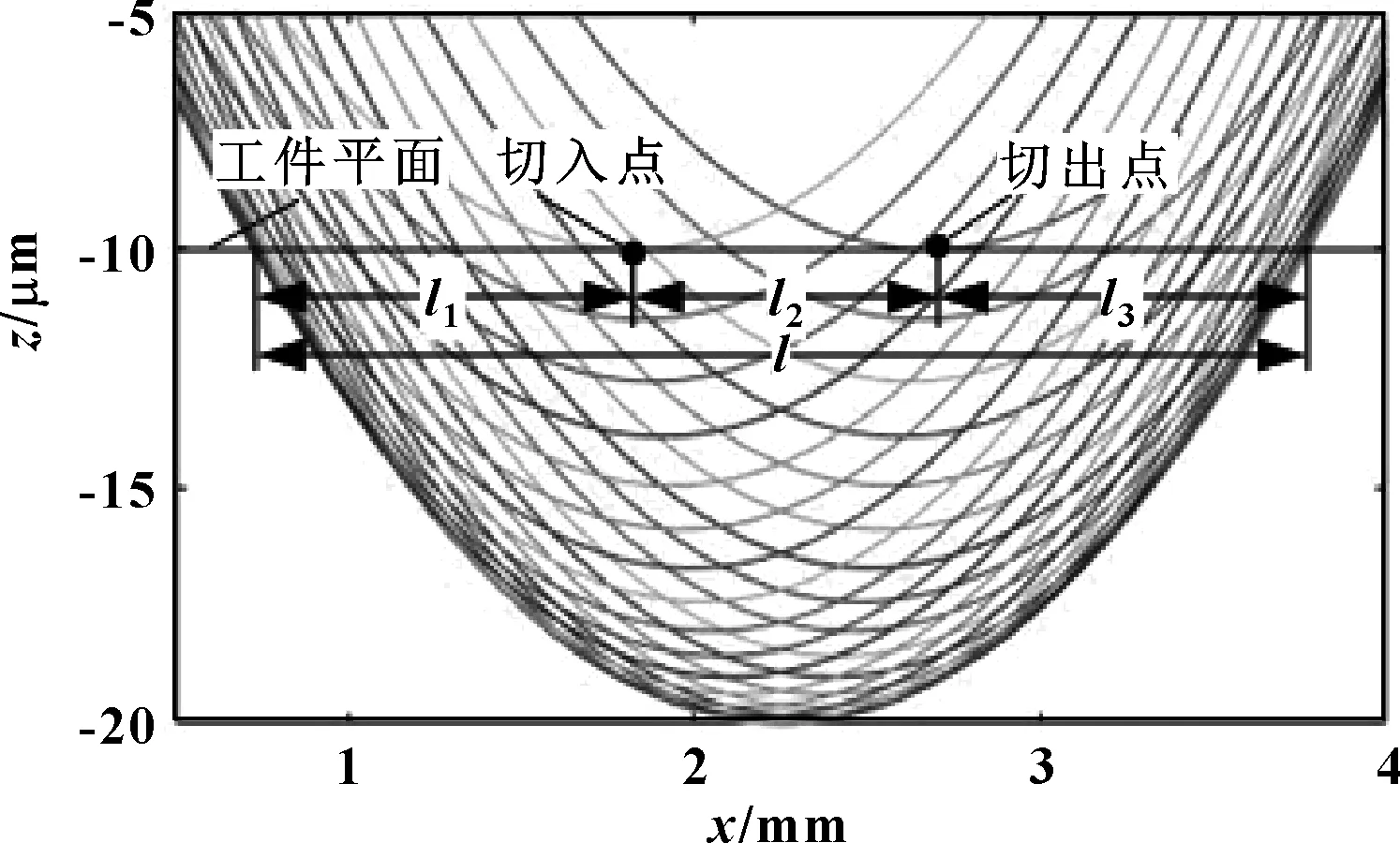
图4 凹坑中心截面形貌
(7)
式中:α为进入磨削状态的磨料簇的圆心角度;β为不同α值时,对应位置磨粒与平面开始接触时的角度;ps为3种排布的速度比。从而得到结构单元长度为
(8)
结构单元间的排布周期为
(9)
由运动学关系可知,当Tx=l时,结构单元相接,凹坑相连;Tx>l时,结构单元相离,可形成凹坑型结构化表面。
2.2 工件与砂轮拓扑映射关系模型
设定工件固定坐标系为工件三维拓扑空间,砂轮固定坐标系为砂轮三维拓扑空间,工件表面结构单元与砂轮磨料簇的拓扑对应关系中,在宽度方向与深度方向为等值变换,在长度方向,由公式(8)可知,受磨料簇形状、速度比、磨削深度等影响,发生拉伸和弯曲变形,且结构单元集合点与磨料簇集合点间存在一一映射关系。设定砂轮磨料簇拓扑特征矩阵与排布特征矩阵为分别为
[Tsd]=[LWH1]T
(10)
[Tsp]=[σxσyδxδy]T
(11)
式中:L、W、H分别为磨料簇的长度、宽度与高度;σx、σy、δx、δy分别为周向与轴向排布周期和相位差。
由这种拓扑变换关系,建立工件结构单元与砂轮磨粒簇之间的拓扑映射关系矩阵[Cd]与排布特征拓扑映射矩阵[Cp]:
(12)
(13)
则工件与砂轮之间的拓扑映射关系为
(14)
2.3 结构化砂轮数学模型
由公式(14)得到砂轮的单元特征与排布特征,在长度方向将结构单元长半轴等分为S份,由公式(1)得到磨料簇离散数学模型-f(s·L/(2S),s·W/(2S)),s=1,2,......,S,得到磨料簇数学模型中各磨粒点坐标(xs,ys,zs)。设定阵列与错位排布砂轮表面磨粒簇周向排列Is列,轴向排列Js行,i=1,2,......,Is,j=1,2,......,Js。对于阵列排布有周向周期σx、轴向周期σy、相位差为0,由此建立阵列排布磨料簇砂轮数学模型:
(15)
错位排布奇数行与偶数行间有周向的相位差δx=σx/2,j为奇数时,数学模型与公式(15)相同,j为偶数时砂轮数学模型为
(16)
叶序排布在砂轮表面排布Ks个磨粒簇,k=1,2,3,......,Ks,周向相位差δx=θ,轴向相位差δy为叶序生长序数c,则数学模型为
(17)
由拓扑映射关系公式(14)和砂轮的数学模型(15)—(17)设计出砂轮,使用MatLab建立图5所示的阵列、错位、叶序排布砂轮模型图,砂轮由砂轮基体与规则排布的磨料簇组成。
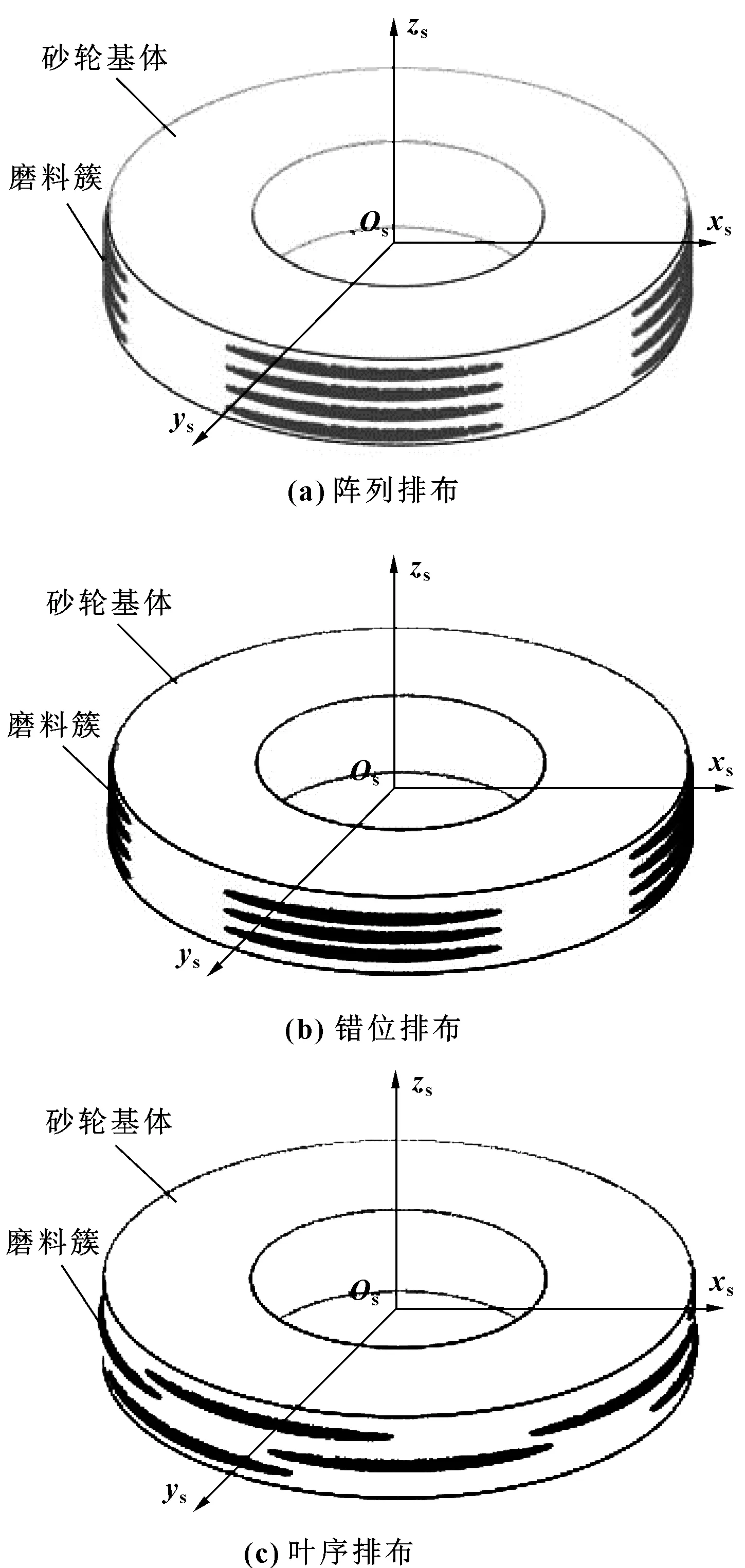
图5 磨料簇砂轮模型
3 磨粒运动轨迹模型
磨料簇砂轮逆磨平面结构化表面,在磨削运动仿真中工件静止,砂轮相对工件运动,砂轮逆时针匀速转动,转速为ωs=2πns/60,砂轮相对工件匀速进给,进给速度为vw,砂轮与工件坐标系之间的距离为e=r+H-ap。数学模型以时间t为变量,控制磨削运动过程,图6为磨削过程示意图。
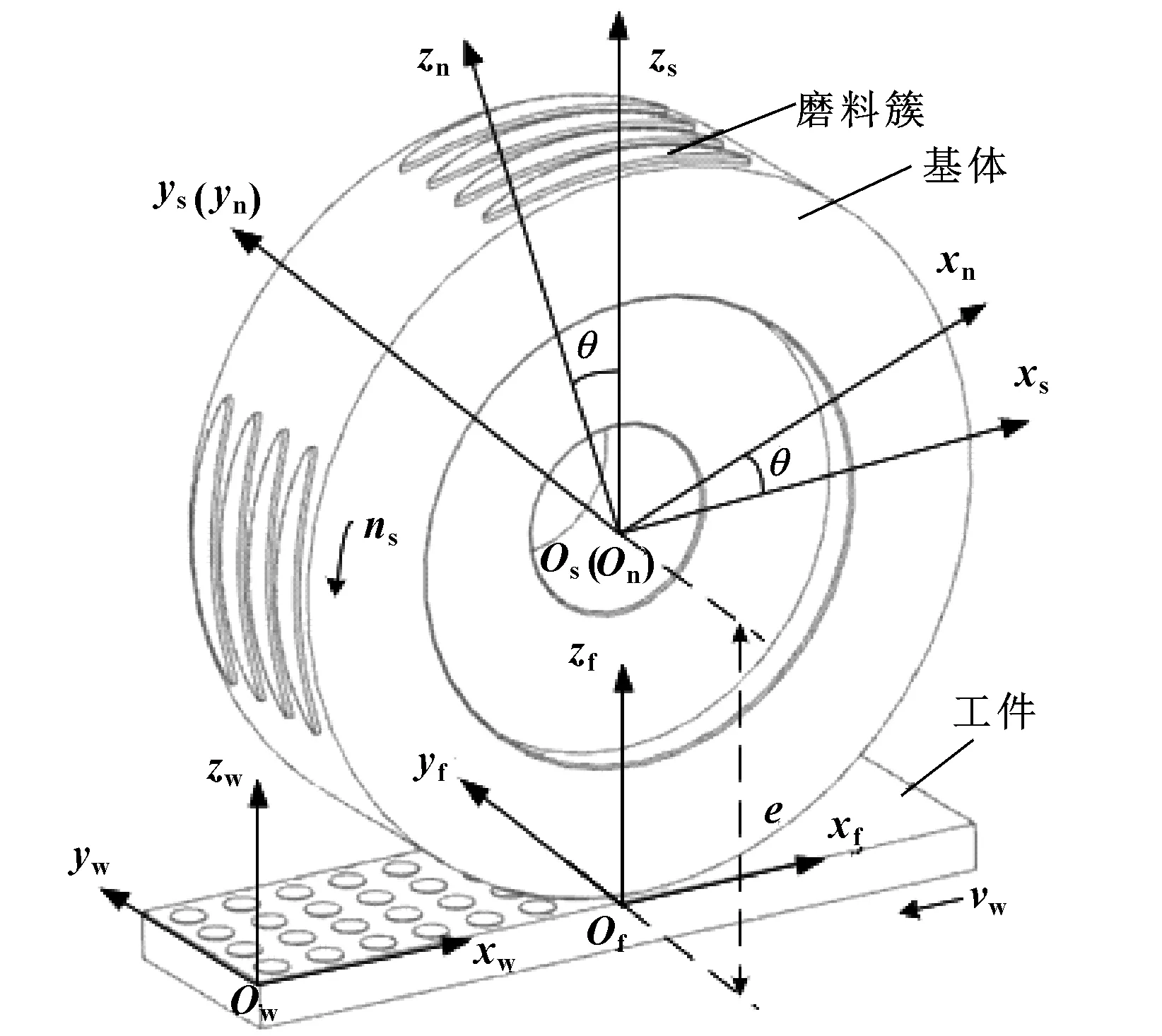
图6 磨削过程示意
定义砂轮固定坐标系Ss(xs,ys,zs),砂轮旋转坐标系Sn(xn,yn,zn),工件进给坐标系Sf(xf,yf,zf),工件绝对坐标系Sw(xw,yw,zw)。通过坐标变换实现从砂轮固定坐标到工件固定坐标系的转换,建立砂轮固定坐标系到砂轮旋转坐标的变换矩阵[Msn],砂轮旋转坐标系到工件进给变换矩阵[Mnf],工件进给坐标系到工件固定坐标系变换矩阵[Mfw],分别为
(18)
(19)
(20)
由变换矩阵(18)—(20)得到磨料簇砂轮上各个磨粒在不同时刻运动轨迹的数学模型:
[Q]=[Mfw]×[Mnf]×[Msn]×[P]
(21)
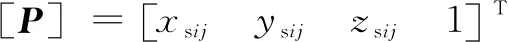
4 仿真结果与分析
根据砂轮数学模型和运动轨迹模型使用MatLab进行仿真。仿真中砂轮基体半径为50 mm,轴向宽度为13 mm,磨粒平均直径为95 μm,磨料簇弧长为30 mm,磨料簇宽度为2 mm,磨料簇最大高度差为20 μm,设定砂轮转速为1 000 r/min,通过控制工件进给速度来控制转速比,研究不同的排布规律、速度比与磨削深度对结构化表面形貌的影响。
4.1 排布对结构化表面形貌的影响
对于阵列排布砂轮,磨料簇轴向排布4行,周期3 mm,周向排布4列;错位排布轴向7行,周期1.5 mm,周向排布4列,偶数与奇数行间相位差1.5 mm;叶序排布轴向相位差0.8 mm,周向相位差为叶序角θ,排布12个磨料簇。设置3种排布的速度比ps分别为12.9、9、9,磨削深度ap=20 μm。仿真形貌分别如图7所示,通过改变结构单元的排布拓扑特征[Tw],可得到不同排布的结构化表面形貌,实现结构化表面形貌的多样化。此时阵列排布为相接的临界状态,而错位排布与叶序排布可在更小的速度比下,形成相离状态的凹坑结构化表面,具有更高的表面占用率。
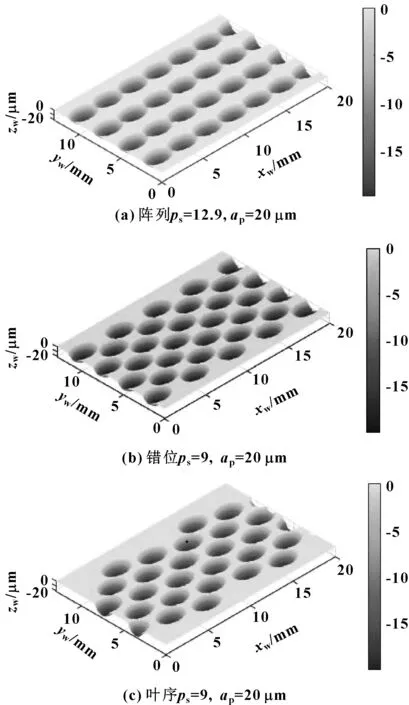
图7 不同排布形貌仿真结果
4.2 速度比对结构化表面形貌的影响
以阵列排布为例,研究速度比对结构化表面形貌的影响。设置磨削深度为20 μm不变,图7(a)和图8(a)、(b)是转速比ps分别在12.9、14和16时工件表面的形貌,结构单元的长度分别为3.18、3.22、3.38 mm,结构单元的排布间距分别为3.18、3.5、4 mm。由仿真结果可知,当l=Tx时,凹坑单元相接处于临界状态,随着速度比进一步增大,结构单元深度h与宽度w不变,结构单元长度l与周期Tx均增大。且进一步研究得,在ps较小时,长度l增长速率较小,ps较大时增长速率较大且趋于线性增长;排布周期Tx与转速比ps成正比例关系,比例系数为σx/(2π),且增大的速率大于单元长度的增长速率。
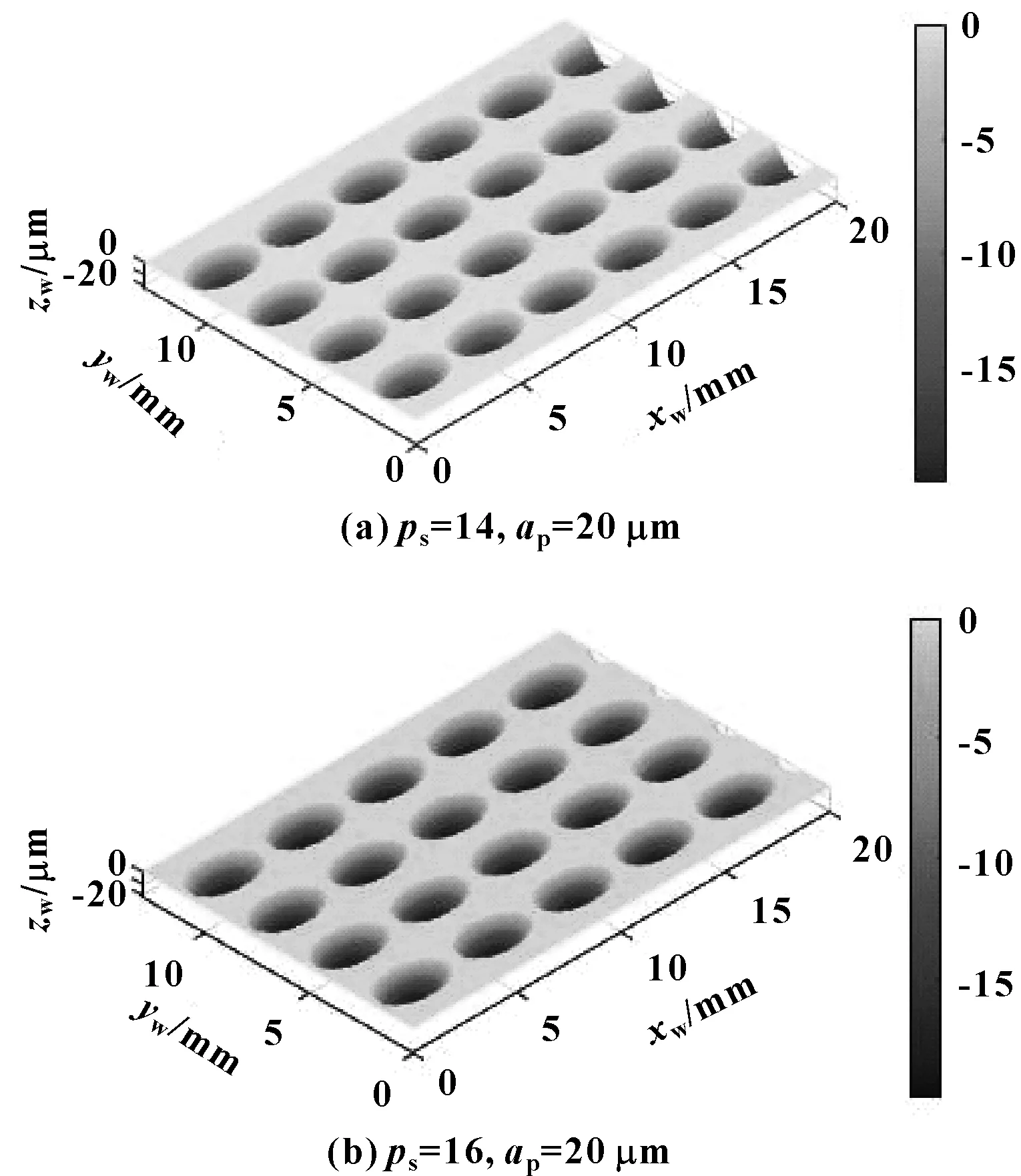
图8 不同转速比形貌仿真结果
4.3 磨削深度对结构化表面形貌的影响
在速度比一定时,研究磨削深度对结构化表面形貌的影响。设置速度比为12.9,图9(a)、(b)和图7(a)是磨削深度ap分别在10、15和20 μm时工件表面的形貌,单元的长度l分别为2.25、2.77、 3.22 mm,单元的排布间距Tx均为3.22 mm。随着磨削深度的增大,单元排布周期Tx值不变,结构单元长度l与宽度w均增大,且增长速率受单元形状影响均逐渐减小。
图9 不同磨削深度形貌仿真结果
5 结论
(1)基于磨削运动学关系与点集拓扑理论,提出拓扑磨削结构化减阻表面的方法,该方法可根据工件与砂轮的拓扑映射关系设计磨料簇砂轮,实现结构化表面形貌多样化,从而加工出特定单元形状与排布规律的凹坑型结构化表面,达到预期的减阻、减磨性能。
(2)通过建立工件与砂轮拓扑空间的映射关系矩阵,设计出磨粒簇砂轮并建立磨削运动轨迹模型,进行拓扑磨削过程仿真,仿真结果表明:工件与砂轮的速度比ps与磨削深度ap是影响结构单元形貌的主要因素。磨削深度一定时,工件与砂轮的速度比增大,结构单元的长度l逐渐增大,排布周期Tx随速度比线性增大,当结构单元长度与排布周期Tx相等时,凹坑单元相接;单元宽度w与周期Ty不变。在速度比一定时,磨削深度越大,结构单元的长度与单元的宽度均越大,且结构单元的排布周期与磨削深度无关。
(3)仿真结果验证了拓扑磨削结构化表面方法的可行性,后续将进行磨料簇砂轮的制造与磨削实验,对上述结论进行实验验证。

