基于核心素养的初中数学日常教学初探

陈建均

【摘要】“直线与圆的位置关系”是初中数学的重要内容，通过这一章节的学习能让学生更好地认识生活，更好地建立起数形结合的思想，也能更好地促进他们核心素养的发展。在探究“直线与圆的位置关系”的过程中能培养学生的高阶思维能力，如分析能力、判断能力和推测能力等，这些能力的发展又为学生核心素养的提升做了铺垫。

【关键词】初中数学;核心素养;直线与圆

《直线与圆的位置关系》这一部分的内容对于初三的学生来说有一定的难度，这一章节的难度体现在各种认知的综合性上，表面上看只是探讨直线与圆的位置关系，实际上所运用的认知却是多方面的，包括勾股定理、三角形、平行四边形、相似三角形和全等三角等方面的认知。这些认知的综合光靠做题、题海战是不能全面提升学生这方面的能力的。因此需要教师改变教学方式，让学生有更多思考的机会，让他们的思维火花尽可能地迸发，让他们找到解决一类问题的密匙，而不只是一两道题目。因此教师要将核心素养的培养落实到这一章节点点滴滴的教学活动中，让学生基于核心素养而学习。

一、立足于学情，把握学生的起点

基于核心素养的初中数学教学的一个首要条件就是教师要能立足学生的学情展开教学活动。学生的学情包含的内容也是多方面的，它包含学生对基础知识的掌握程度，也包含学生的思维特点、情感态度和学习方式等。学情是学生在某一个数学章节的综合表现，要让学生学习相关的认知，要提升他们某一方面的能力，就要立足他们的学情，做到有的放矢，不能盲目提升。当前的数学教学中存在不顾学生学情而进行教学的现象，有时候教师讲授的内容超出了大多数学生的能力范围，又或是大多数学生都会的内容，教师还在反复地讲。立足学生的学情，一点点地铺垫，让学生拥有一个扎实的起点，其更多素养的生成自然就指日可待。

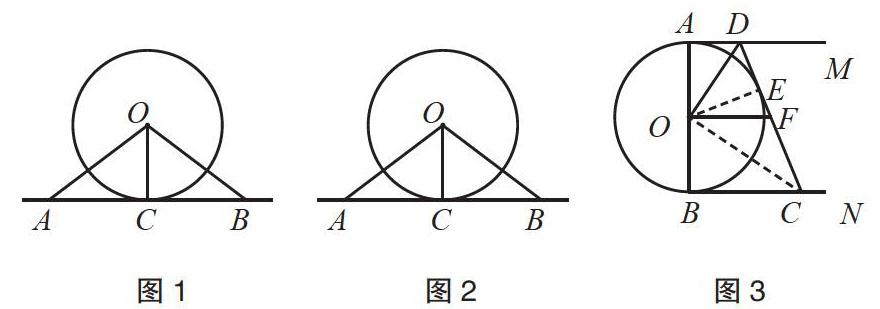
以下面这题为例，如图1所示，直线AB经过⊙O上的点C，并且OA=OB，CA=CB。求证：直线AB是⊙O的切线。

这是这一章节一道基础的题目，学生只要连接OC，从OA=OB这一条件出发，就能推断出△AOB是等腰三角形;接着再从CA=CB这一条件入手，推断出OC⊥AB;最后学生再结合“直线AB经过⊙O上的点C”这一条件得出直线AB是⊙O的切线。由学生做题过程，教师基本能推断出这样的学情，即，学生知道运用切线判定定理需满足两个条件：①经过半径外端;②垂直于这条半径。教师再次设计的题目就要以这个学情为基准进行适当的拓展，也就是要让学生沿着这个起点往纵深奔跑。于是教师设计这样的题目：如图2，已知OA=OB=5厘米，AB=8厘米，⊙O的直径为6厘米。求证：AB与⊙O相切。学生运用到这一章节中辅助线的作法：过O点作OC⊥AB交AB于C点。他们先是证明△AOB是等腰三角形，再推断出：CA=CB=，AB=4厘米;最后由OB=5厘米，运用勾股定理得出OC= 52+42 =3厘米。因为⊙O的半径为3厘米，所以AB与⊙O相切。从这题当中能明显地发现学生知道切线的三种判定方法，这题运用到的是直线到圆心的距离等于该圆的半径。知道这些学情之后，教师要基于这样的起点促进学生生长。教师问，以上两例辅助线的作法是否相同？有什么规律可以找寻？明显地，基于核心素养的初中数学教学要能贴着学生的最近发展区，让他们适切地生长。

二、创设有效情境，培养学生的直观想象力

初中学生有一定的直观思维能力，相对于抽象思维，在这一方面是他们的一个优势，他们对着一些具体的画面能展开丰富的联想。作为数学教师要进一步培养学生的直观思维，进而让他们建立起严密的数学思维。同时，直观思维能帮助学生提升数学实践能力，增强创新意识。教学中教师要尽量给学生创设激发直观思维的机会，让他们拓展这方面的能力。一般来说，初中学生需要具备六项数学核心素养，直观思维是一个重要的素养，是产生其他能力的基础。有了直观思维，学生才能构建抽象的数学认知结构，进而进一步理解相关事物的本质。换言之，直观思维是探索数学推理过程的前提，是形成论证思路以让数学回归现实世界的主要方式。当前笔者所列举的《直线与圆的位置关系》是初中重要的平面几何认知，与学生生活、现实空间都有着明显的联系。学生在学习过程中能得到直觉上的支持，再加上这一章节的综合性，许多题目有着多样的形式结构，这些都为培养学生的直观想象能力创设了极好的条件。

就以往的经验来看，在教学过程中教师没有利用好这一章节切实地落实学生的直观想象素养。如果学生的直观想象素养得到了提升，他们就能发现解决问题的思路，进而促进多元思维的发展。

教师在讲解直线与圆的关系时，没有直接从书上的概念入手，也没有在黑板上展示相关的图片，而是在早上将学生带到一个湖边，让他们趴在栏杆上看日出。对于这样的情境，学生感到新奇，自然就愿意投入其中。学生一開始看到的是太阳还没有从湖面上升起来，用他们自己的话说，看到的只是害羞的太阳的小半个脸。教师问学生：如果从数学的角度来看，这是一幅怎样的几何图形？学生盯着远处还没露出水面的太阳说，是不是一条直线与半个圆，如果想象一下的话，应该是这条直线穿过这个圆。学生继续观看，他们看到太阳正好从地平线上出来了，教师问：这是一个怎样的图形呢？学生想了想说，一条直线贴着圆走过，好像要与圆相交，又好像要与圆分离。这一刻学生还没有接触到切线的概念，他们用自己的语言描述了这样一个关系。可以确切地看到，教师创设这样的情境，让学生的直观思维充分展现了出来。再接着，学生看到了太阳离开了地平线，越过了周围的一些建筑物，用学生的话说，直线与圆越来越远了。教师让学生将看到的日出场景以简笔画的形式表现出来，学生画出的就是三个不同的直线与圆的位置图。带着具体的景象，带着刚才的想象，学生更容易在所画的图像中研究直线与圆关系的内核。可见，教师要多创设真实有效的情境，让学生的直观思维飞起来，进而激发其他思维。

三、设计教学活动，提高学生的逻辑推理能力

数学是思维的体操，思维与数学是紧密联系在一起的。教师在教学中不注重培养学生的思维能力，那么学生的数学能力也得不到根本的发展。思维能将数学教学推向深远，能让学生进入深度学习的状态。逻辑推理能力是重要的思维能力，是关键的数学素养。当学生拥有一定的逻辑推理能力，他们就能自己构建起一定的数学知识体系，就能够自主地、严谨地思考问题。在《直线与圆的位置关系》这一章节的学习中，教师要给学生提供逻辑推理的条件与机会，就是要让他们自己参与到具体的数学活动中来，让他们自己去体验、猜想、实验、推理和论证。这一系列的数学活动其实就是逻辑推理能力产生与发展的过程，在这个过程中，教师要做好指导工作，要让学生掌握正确的方法，进而提升他们的逻辑推理素养。

以图3为例，AB是⊙O的直径，AM和BN是它的两条切线，DE切⊙O于点E，交AM于点D，交BN于点C，F是CD的中点，连接OF。教师先问学生：OD与BE有怎样的位置关系？学生先是根据题目中的文字说明将图形画出来，也就是说，学生在猜想之前先是动手作图。图形画出来之后，学生通过直接的观察，发现OD与BE应该平行，这是他们的猜想。接着他们就开始推理，依据一般的作辅助线的规律，学生先是连接OE，从AM、DE是⊙O的切线，OA、OE是⊙O的半径等条件出发，得出：∠ADO=∠EDO，∠DAO=∠DEO=90°，∠AOD=∠EOD=∠AOE，再结合∠ABE=∠AOE，推断出：∠AOD=∠ABE，OD∥BE。为了进一步提升学生的推理能力，教师让学生猜一猜图中还有哪些线段存在一定的等量关系。要想猜，就需要实验。学生将图形剪下来，进行一定的拼凑，他们发现OF可能只有CD的一半。明显地，学生已经掌握了一般的推理过程，即，需要亲手操作或者从实验入手，再做大胆的设想。学生发现BC、CE是⊙O的切线，这一条件还没有利用，他们连接OC，进而得出：OCB=∠OCE。他们再从AM∥BN出发，推断出∠ADO+∠EDO+∠OCB+∠OCE=180°。接着他们由∠ADO=∠EDO，得出2∠EDO+2∠OCE=180°，即∠EDO+∠OCE=90°。最后他们利用Rt△DOC中F是DC的中点这一条件，得出OF=CD。总之，教师要多创设需要进行逻辑推理的数学活动，让学生的思维得到充分锻炼，让素养喷薄生长。

四、结束语

初中数学学习是义务教育阶段第三学段的数学学习，要凸显其基础性和生长性，一方面要注意知识的学习起点，即知识从哪里长出来，另一方面要注意知识的延伸性，即知识最终走向哪里，教师必须从整体上把握知识的结构。在把握知识整体架构的前提下，教师要在初中数学学习过程中着眼于发展学生的学习能力，不能局限于掌握数学知识本身，更多地关注学生在学习过程能力的发展、素养的提升。因此，教师要从发展学生的核心素养出發，抓实日常的课堂教学，在学习过程中培养学生的核心能力，使其养成核心素养。

【参考文献】

[1]韦丽云.“构建初中数学高效课堂教学模式”再思考——以“直线与圆的位置关系”教学为例[J].中学数学教学参考，2017（18）.

[2]顾靖楠.例谈初中数学概念课的教学——以《直线与圆的位置关系（1）》为例[J].好家长，2017（13）.