RV减速器主轴承拟静力学模型简化分析方法
陈瑛琳,史文华,陈江义,秦东晨,袁峰
(郑州大学 机械与动力工程学院,郑州 450001)
为满足RV减速器外形尺寸小,承受扭矩大的工作需求,其主轴承往往采用薄壁、多球结构[1]。球数增多会导致轴承受力和变形计算量大幅增加,求解速度慢。如何快速计算和分析RV减速器主轴承的受力和变形是一个亟待解决的问题。
常用的轴承设计方法为数值分析法[2],其中的拟静力学方法适用于高速、重载场合,计算速度快,是目前应用广泛的方法之一[3-6],该方法以赫兹理论[7]为基础,考虑离心力、陀螺力矩作用,采用沟道控制假设,可分析球和沟道在点、线接触下的载荷分布和接触变形[8]。文献[9-10]的实践证明该方法在内、外圈接触角差异较大时具有良好的数值稳定性和较高的计算精度。
拟静力学法中求解非线性方程组多采用牛顿-拉弗森算法,求解简单但对初值敏感,且方程组的数量随球数增加而成倍增加,求解速度也相应变慢。针对该问题,文献[11]在算法中引入迭代步长松弛因子,并采用二分法对松弛因子的取值进行优化,同时通过矩阵变换简化了雅克比矩阵求解过程,从而缩减了迭代时间;文献[12]对迭代公式进行改进和修正,降低了因初值偏差给收敛性带来的影响;文献[13]建立迭代约束条件,使迭代能在合理范围内进行;文献[14]提出减少非线性方程数量和迭代变量约束的方法,提高了方程组求解的效率。然而,对于RV减速器主轴承,未知数和方程组数量较多,即使采用优化算法,也难以快速得出结果[15]。文献[16]提出可将滚子轴承沿受载方向视为对称,非承载区滚子受力情况视为相同,减少了方程数量,使未知参数减少近一半,从而快速计算;但在大扭矩作用下,RV减速器轴承载荷分布复杂,在三维空间内并不沿载荷方向对称分布,该方法理论上不再适用。
鉴于上述原因,在建立RV减速器主轴承(角接触球轴承)拟静力学模型的基础上,针对球数较多导致非线性方程组数量成倍增加,求解难度增大的问题,提出一种复杂工况下的简化分析方法,并从计算速度和分析精度两方面与原方法进行对比。
1 RV减速器主轴承拟静力学模型
为便于表述,省略部分球,角接触球轴承球的角位置关系如图1所示,以轴承中心为原点,轴向中心线为z轴,建立坐标系Oxyz。球之间的夹角Δψ=2π/Z(Z为球数),设定第1个球的位置角为γ,则第j个球的位置角ψj=2π(j-1)/Z+γ。

图1 球角位置示意图Fig.1 Diagram of ball angle position
在力Fx,Fy,Fz和力矩Mx,My作用下,轴承发生非线性偏移,原有几何接触关系也发生改变。假定轴承外圈固定,则第j个球的中心和内外圈沟曲率中心的位置关系如图2所示。若内圈沟道相对外圈沟道分别沿x,y,z轴方向产生偏移δx,δy,δz,绕x,y轴中心线方向产生角度偏转θx,θy,则在位置角ψj处内外圈沟曲率中心的轴向距离A1j和径向距离A2j可表示为

图2 载荷作用前后第j个球中心和内外圈沟曲率中心的位置关系Fig.2 Position relationship between j-th ball center and curvature center of inner and outer groove before and after loading
(1)
Gi=Dpw/2+(fiDw-Dw/2)cosα0,
式中:A为受载前轴承内外圈沟道中心的距离;α0为轴承初始接触角;Gi为内沟道转动半径;Dpw为球组节圆直径;Dw为球直径;fi为内沟曲率半径系数。
为简化计算,引入变量X1j,X2j,分别表示受载后球中心到外沟曲率中心之间的轴向和径向距离。根据勾股定理可得
(A1j-X1j)2+(A2j-X2j)2-[(fi-0.5)Dw+δij]2=0,
(2)
式中:fe为外沟曲率半径系数;δij,δej分别为受载后内、外圈沟道的法向变形。
用A1j,A2j,X1j,X2j分别表示受载后轴承内、外圈的实际接触角αij,αej,即
(3)
为减少计算量,提高迭代速度,联立(2),(3)式,将δij,δej,X1j,X2j用αij和αej表示,可使未知数减半,其转换公式为
(4)
对垂直于轴承轴线并通过第j个球中心的平面进行分析,球受到内外圈沟道接触载荷Qij和Qej、离心力Fcj、陀螺力矩Mgj和摩擦力作用(图3)。若非共面的摩擦力很小,可以假设陀螺力矩Mgj完全被球与外圈沟道接触区的摩擦力所阻止,取陀螺力矩作用控制系数λij=0,λej=2,若条件不满足,则取λij=1,λej=1。

图3 第j个球所受载荷Fig.3 Load on j-th ball
由赫兹接触理论可知任意位置角ψj处球的法向载荷与法向变形的关系为
(5)
式中:Qij,Qej分别为内、外圈与球的法向接触载荷;Kij,Kej分别为内、外圈沟道位移-载荷系数。
单个球所受离心力Fcj为
(6)
式中:m为单个球质量;ωmj为球公转角速度。
陀螺力矩Mgj可表示为
Mgj=JωmjωRjsinβj,
(7)
式中:J为球转动惯量;ωRj为球自转角速度;βj为球姿态角。
由图3球受载情况可知单个球在竖直方向和水平方向的受力平衡,平衡方程为
(8)
根据轴承整体所受力和力矩的平衡关系,可得轴承平衡方程组为
。(9)
2 简化分析方法
传统拟静力学方法通过(8),(9)式迭代求解,在此基础上,针对RV主轴承的多球特性,设计了1套RV减速器主轴承拟静力学模型简化分析方法,计算流程(图4)为:

图4 RV减速器主轴承拟静力学分析流程Fig.4 Analysis process of quasi-static model of main bearing for RV reducer
1)假定轴承处于静止状态,采用静力学方法求解轴承在静载荷下的内外圈沟道接触角、位移和变形等参数。以静力学计算结果为基础,求解轴承运转时各零件的速度、陀螺力矩、离心力等参数。
2)假定轴承位移参数δx,δy,δz,θx,θy不变,且第1个球的位置角γ为0,以静力学算法求解的位移和角度作为初值,对 (8)式进行迭代,求得轴承内、外圈动态接触角αij和αej。
3)将接触角代入(9)式进行迭代,求得新的轴承位移、法向变形以及所受载荷等参数。判断新位移参数δx,δy,δz,θx,θy是否达到平衡,若是则输出结果,若否则更改第1个球的位置角γ,重新计算参数,不断重复直至位移参数满足精度要求。
该流程中迭代算法以牛顿-拉弗森算法为基础,增加迭代步长松弛因子,保证每次迭代都使方程的绝对值减小,避免迭代跳出范围,造成不收敛。同时,对角度迭代中的变量进行判断和修正,避免出现死循环。
该算法中方程组数量为2Z+5,RV主轴承球数较多,则方程组求解易出现迭代缓慢,难以达到精度等问题,有必要对其进行简化。因为球排列密集时,相邻球受力相似,接触角相近,假设相邻k个球接触状态一致,在计算中将其作为完全相同的零件进行处理,进而成倍减少方程组数量。
若原球数Z可被k整除,则简化后的球数N=Z/k,第j个球的位置角ψ′j=2π(j-1)k/Z+γ,则(9)式中x方向受力平衡方程可转换为
(10)
若Z不能被整除,且余数为h,则球数N=[Z/k]+1,(10)式可转换为
(11)
同理可对其他几个力和力矩平衡方程式进行简化,替代(9)式进行计算。
3 实例分析
以某减速器用主轴承H76/182RV角接触球轴承为例分析,其主要结构参数见表1。

表1 H76/182RV角接触球轴承主要结构参数Tab.1 Main structural parameters of H76/182RV angular contact ball bearing
轴承转速n取40 r/min,施加径向载荷Fy=4 000 N,轴向载荷Fz=13 720 N,力矩载荷My=2 450 N·m,按k个球进行分组,分别取k=1,2,3,4(k=1表示没有简化的情形)。采用上述简化模型计算轴承第1个球与内圈的法向载荷以及接触角,其结果如图5和图6所示。由图5可知:当k为2,3,4时,球所受内圈的法向载荷与未简化时的法向载荷有相同的分布趋势;k取2时,计算结果与未简化模型结果几乎一致,k值增大,求解结果与未简化模型结果差异增大,但误差仍能满足基本的工程需求。由图6可知:简化前后内圈接触角曲线分布几乎相同。由此可知简化模型是合理的。

图5 简化与原算法计算所得第1个球与内圈的法向载荷Fig.5 Normal load of first ball and inner ring calculated by simplified and original method
为进一步检验算法是否在不同工况下都适用,根据RV减速器所能承受的最大载荷和转速,分别取轴承转速n为20~200 r/min,轴向载荷Fz为1 372mN,径向载荷Fy为500mN,力矩载荷My为245mN·m(m为工况载荷系数,m=1,2,…,10)。取k为1,2,3,4,记录不同工况下程序实际计算时间,结果见表2。并以内外圈沟道在x方向的相对位移δx为参数,计算在不同工况下简化算法与原算法的相对误差,结果如图7和图8所示。

表2 不同工况下简化算法的计算时间Tab.2 Calculation time of simplified method under different operating conditionss

图7 转速为40 r/min时不同载荷下内外圈沟道相对位移δx的相对误差Fig.7 Relative error of relative displacement δx of inner and outer raceway under different loads at rotational speed of 40 r/min
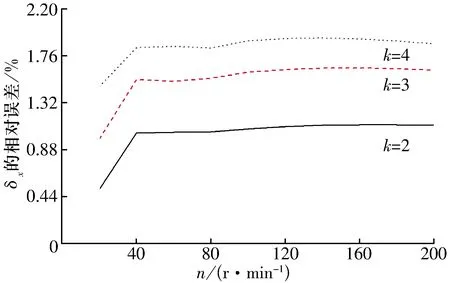
图8 Fy=5 000 N,Fz=13 720 N,My=2 450 N·m时不同转速下内外圈沟道相对位移δx的相对误差Fig.8 Relative error of relative displacement δx of inner and outer raceway under load of Fy=5 000 N,Fz=13 720 N,My=2 450 N·m and different rotational speeds
由表2可知:采用简化分析方法能够有效地提升计算效率,减少计算时间。由图7、图8可知,不同转速和载荷工况下简化算法与原算法的相对误差都在3%以内。故可认为载荷和转速对于简化分析方法的求解精度影响不大,简化算法在任意载荷和转速工况下都具有适用性。
4 结束语
建立了RV减速器主轴承拟静力学分析模型,并针对其多球特性导致的数值分析计算量大,求解缓慢的问题,提出了一种简化分析方法,该方法假设相邻k个球所受的接触载荷及接触角相同,可以简化为1个零件进行计算。并以某减速器主轴承H76/182RV角接触球轴承为例,对该方法进行验证,结果表明简化方法能有效提高计算效率。当k=2,3,4时,简化分析方法误差都小于3%,可以满足工程需要。该简化方法的计算精度受载荷和转速影响较小,误差在较小范围内波动,可以认为该简化分析方法适用于不同的载荷和转速工况。提出的方法不仅可以用于RV减速器主轴承的拟静力学分析,还适用于球数较多的其他角接触球轴承。

