对立式圆筒形储罐标准GB 50341—2014中某些问题的探讨
李 冰,丁天才
(中石化宁波工程有限公司设备室,浙江 宁波 315103)
1 自支撑式罐顶顶与壁的弱连接问题
GB 50341—2014(以下简称标准)中关于罐顶与罐壁弱连接结构的要求之一“连接处的罐顶坡度不应大于1/6”[标准中第7.1.6条1款1)项]对于罐顶为自支撑式结构的储罐几乎是不可能达到的,理由如下(所有符号说明见文末)。
1.1 对于锥顶
对于自支撑式锥顶:1/6(tan9.5°)≤tanθ≤3/4(tan37°)(7.3.1条);
对于柱支撑式锥顶:tanθ≥1/16(tan 3.5°)(7.4.1条)。
上述条件说明,只有θ=9.5°的自支撑锥顶罐(无实际意义)以及3.5°≤θ≤9.5°的柱支撑锥顶罐才能满足弱顶连接规定中关于罐顶坡度的要求。
1.2 对于拱顶
一般取Rs=(0.8~1.2)D,则

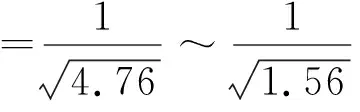

=24.6°~38.7°≫9.5 °[即arc tan(1/6)]
上述推论说明,拱顶罐的罐顶结构根本无法达到弱顶连接规定中关于罐顶坡度的要求。
既然自支撑式拱顶结构罐顶与罐壁的连接不可能为弱顶结构,则说明标准第7.1.6条关于弱连接结构的要求有局限性。该条规定实际上仅适用于θ≤9.5°的柱支撑锥顶罐,建议标准中加以说明。
2 抗压(拉)环总面积A的问题
2.1 计算公式[标准中式(7.1.6)]关于罐体材料的适用性讨论
暂且将由罐壁及罐壁、罐顶结构件组成的无顶板部件称为网架顶钟罩。该钟罩在罐顶与罐壁连接部位的重力传递情况以及抗压(拉)环受力分析见图1。
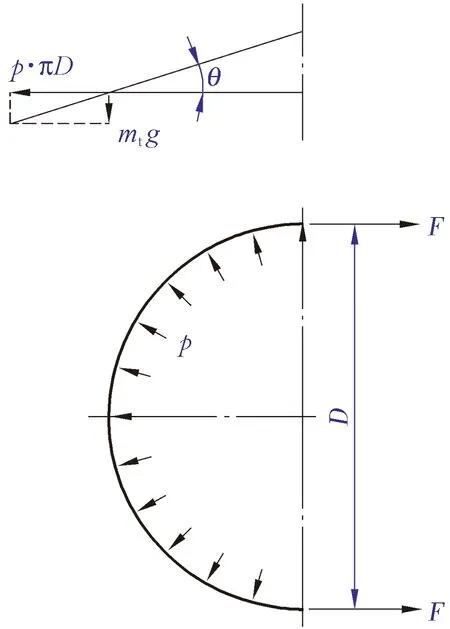
图1 承受外压时顶壁连接处力的传递与抗压(拉)环受力分析
抗压(拉)环所受的拉力
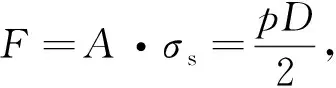
故抗压(拉)环面积
1) 对于Q235B(Q235C),取σs=225 MPa作为抗压(拉)环破坏时的屈服强度,则
如需保证网架顶钟罩在被提起的瞬间抗压(拉)环首先被破坏,则应满足

2) 对于其他牌号材料,应满足
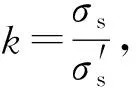
(1)
如果直接采用标准中的计算公式确定抗压(拉)环的总面积,对于除Q235系列外的其他碳钢、低合金钢储罐,因A的最大值较真实控制值大,不能确保抗拉(压)环首先破坏,罐体将存在安全隐患;对于奥氏体不锈钢储罐,则因其A的最大值较真实控制值小,而导致储罐整体的承压能力下降。
2.2 标准中定义的有效面积A与其真实有效面积Ae的本质不同
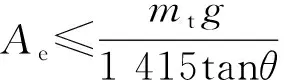
在储罐的整个使用年限内,均应确保在网架顶钟罩被提离瞬间,抗压(拉)环在网架顶钟罩自身重量的作用下首先破坏(破坏由拉应力造成,故该环此时被称为抗拉环)。如果按有效厚度来计算并控制抗压(拉)环的总面积,则仅仅在储罐使用即将到期的最后时刻才能保证抗压(拉)环先破坏(在如此短的时间段罐内超压的概率极低),而在其余绝大部分操作期间罐壁与罐底连接区域先于抗压(拉)环破坏的可能性一直存在,储罐“先上后下”的预期破坏顺序必然得不到实现,故面积A的最大值计算本身也就失去了意义。
因此,标准中对于A的“有效截面面积”的定义不够严谨,甚至具有一定的误导性。其“有效”的真实含义并非是指从各元件名义厚度中扣除腐蚀裕量,而是指参与面积计算的各元件的有效计算长度。
3 计算破坏压力计算公式错误的问题
罐顶与罐壁连接部位的一定区域参与抵抗由罐顶所传递过来的力,该区域习惯上被称为抗压(拉)环。当该区域内的金属达到材料的屈服点时,罐内所对应的内压力即为抗压(拉)环的计算破坏压力。
将罐顶板及其上的附件顶起需要的内压力
罐顶板(及其上的附件)被顶起后,内压继续上升,直至抗压(拉)环屈服破坏(破坏由压应力造成,故该环此时被称为抗压环)。在此期间,带顶板钟罩(即网架顶钟罩与顶板组焊后)在罐顶与罐壁连接部位的重力传递情况以及抗压(拉)环受力分析见图2。
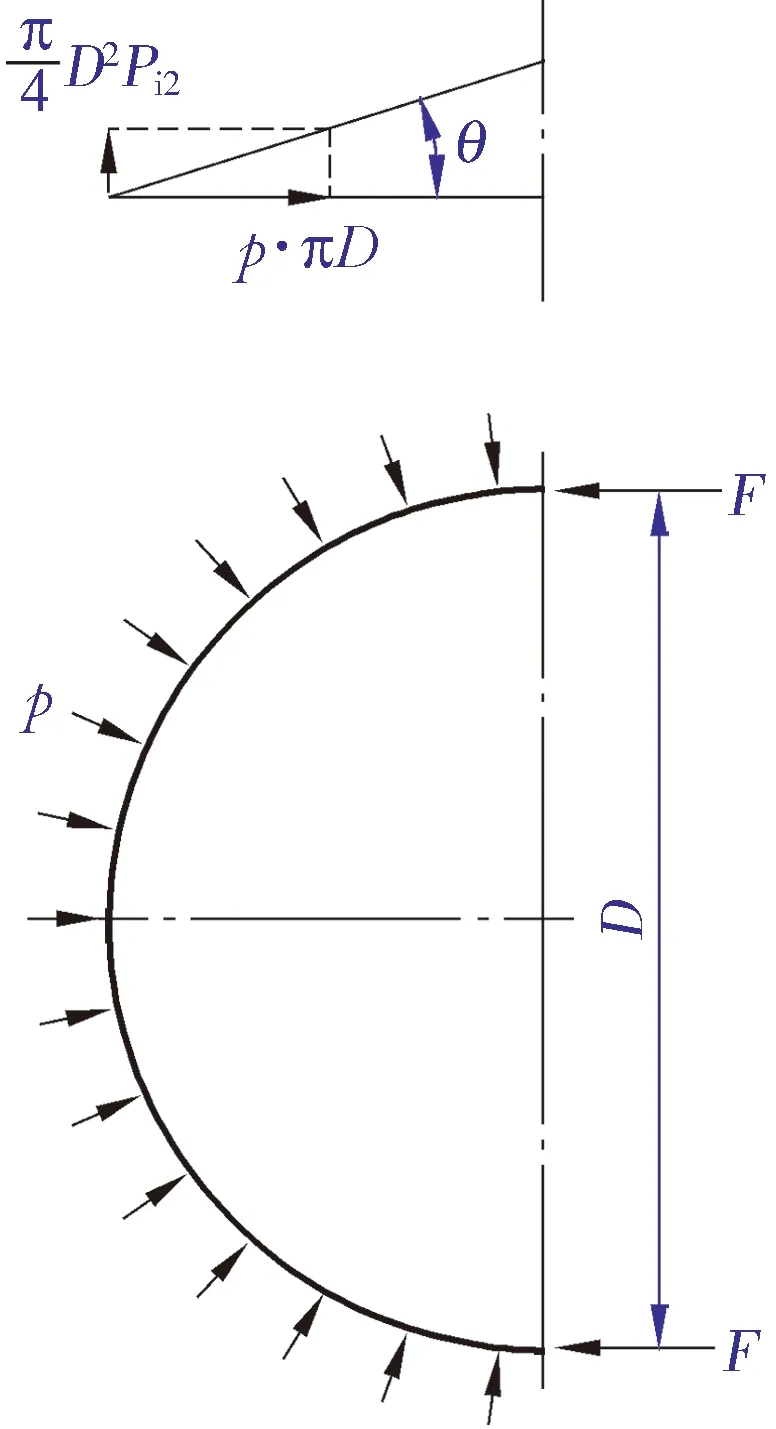
图2 承受内压时顶壁连接处力的传递与抗压(拉)环受力分析
内压下罐顶被顶起(即抵消罐顶重量)之后所受到的上升力与抗压(拉)环所受的周向压缩力之间的关系为
所以
抗压(拉)环所受的内力与罐壁所承受的压力之间的关系为
2F=pD
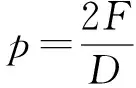
而F=Aσs
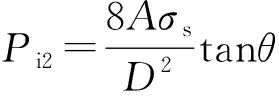
因此,计算破坏压力(单位换算后)
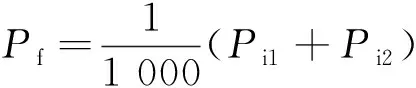
(2)
用[σ]取代式(2)中的σs,得到最大设计压力Pi
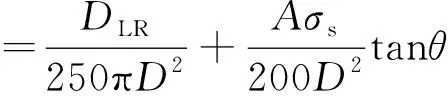
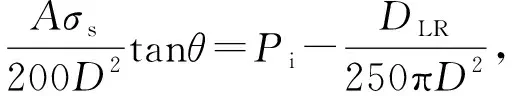
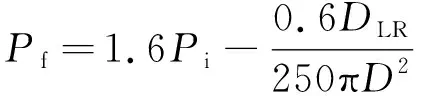
(3)
故标准中式(A.3.5)中的系数“0.000 746”可能是笔误,正确值应为“0.000 764”。
4 外压(Pe>0.25 MPa)储罐某些计算不必满足常压储罐相关规定的问题
4.1 关于拱顶板计算厚度的计算
由外压及常压拱顶板计算厚度公式得
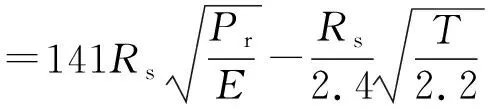
其中,取E最大值为2.01×105MPa,则罐顶设计总外压(标准的正文以T表示,标准的附录B则用Pr表示)T=DL+W+(0.4~1.0)·Pe。
又Pr>T(因外压Pe>常压Pe),
故td-trs>0, 即td>trs
上述推论说明,外压储罐拱顶板计算厚度恒大于常压储罐,故标准第B.2.4条第1款的规定没有必要。
4.2 关于抗压(拉)环所需面积的计算
由外压及常压时抗压(拉)环所需面积计算公式得
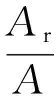
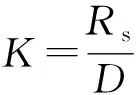
则
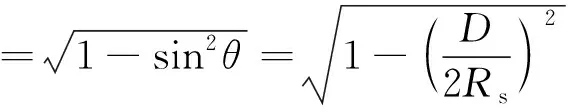

上述推论说明,外压储罐抗压(拉)环所需面积恒大于常压储罐(相差20%以上),故标准B.2.4条2款规定没有必要。
5 正文与附录B关于罐壁稳定计算相互矛盾的问题
5.1 罐壁外压稳定计算公式的推导
罐壁外压稳定计算是以米赛斯(R. V. Mises)公式经简化后得到的近似公式为基础的,该简化式亦称为拉姆(B. M. Lame)公式,其表达式为
(4)
对于常压储罐,取稳定安全系数m=1、E=2.01×105MPa,经单位换算后,式(4)变形为

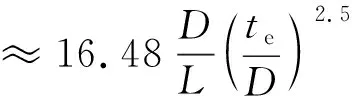
(5)
将L=HE、te=tmin代入式(5),即得到标准中的式(6.4.3-1)。
对于外压储罐,取稳定安全系数m=1.25ψ,并经单位换算,则式(4)变形为
故
(6)
将L=Hsafe、te=tsmin、 [Pcr]=Ps代入式(6),即得到标准中的式(B.3.4)。
5.2 常压条件下罐壁的外压稳定安全系数相互矛盾
当Pe≤0.25 kPa时,罐壁的外压稳定计算有正文中式(6.4.3-1)及附录B中式(B.3.4)两种形式。通过上述公式推导过程得知,两者关于罐壁的稳定安全系数分别取为“1.0”及“1.25”(按B.3.2条第1款规定,此时取ψ=1),故该标准正文与附录B在Pe≤0.25 kPa时是相互矛盾的。附录B中不应包括Pe≤0.25 kPa的常压条件,应将B.3.2 条第1款规定删除。
6 关于作用于外压储罐罐壁上的设计风压W的计算问题
倘若根据标准附录F表F.0.1中关于W的说明,外压储罐罐壁设计风压按W=1.23ω0计算,则


对于A、B、C、D类四种地面粗糙度区域,根据标准中表6.4.5-1“风压高度变化系数μZ”,μZ分别取1.09、1.00、0.65、0.51,则有


实际上,在C类(有密集建筑群的城市市区)及D类(有密集建筑群且房屋较高的城市市区)地面粗糙度类别的地区,建造盛装易燃易爆甚至有毒介质的石化储罐几乎是不可能的。这样,则有
即外压储罐罐壁的设计风压不会超过常压储罐的0.55倍。在实际工程设计中,外压储罐罐壁加强圈少于常压储罐这种不合理现象是经常发生的(Pe>0.25 MPa的外压界定条件使绝大部分储罐很容易被划入外压储罐类,这表面看似对承受外压的储罐提高了要求,但实则使设计出的外压储罐变得更不安全)。
应该说,储罐罐壁所承受的风压大小,除与基本风压、地面粗糙度类别、储罐的质心标高以及罐体几何尺寸等有关外,与罐内是常压还是负压无关。因此,对于内部为负压的外压储罐,作用于罐壁上的风压也应取W=2.25μZω0[参见标准中的式(6.4.3-5)及式(6.4.3-6)],而绝不应取为W=1.23ω0。
7 外压增加时罐壁加强圈数量不增反降的问题
7.1 问题的根源
综合上述,由外压储罐罐壁稳定安全系数的取值与标准附录B中B.3.2条的规定可看出,罐壁的稳定安全系数m的取值是变化的。考虑其使用的安全可靠性,m随外压的增加而相应增大,最大可达1.25×3=3.75,此值比压力容器筒体外压稳定安全系数“3”高出1/4。
但在实际计算时,却出现了外压增大而罐壁的稳定安全系数m反而变小的情况。现通过对稳定系数ψ取值进行讨论,分析该现象出现的原因,并提出避免这种不合理情况的建议。
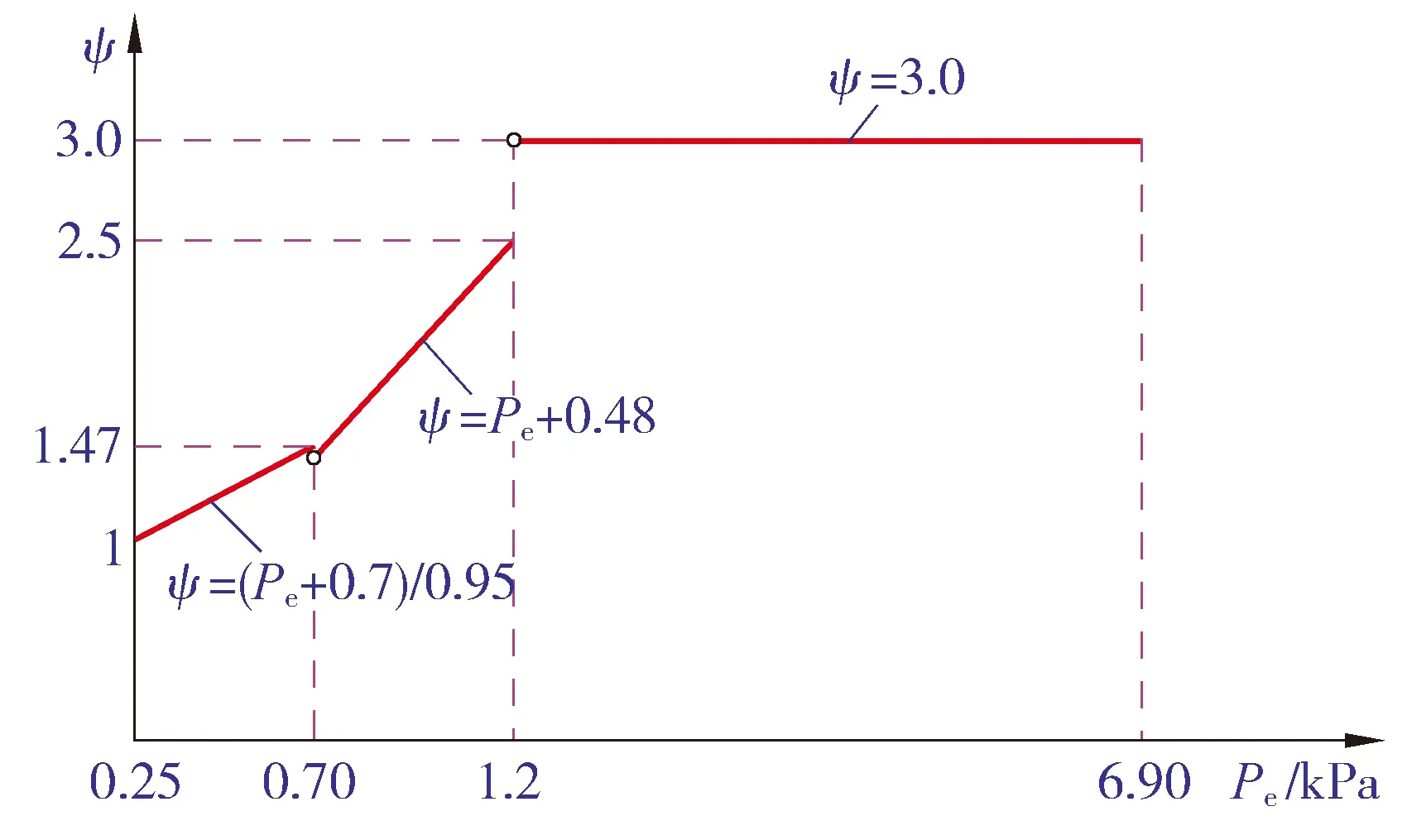
现将B.3.2条规定所对应的曲线绘制成图3,其中稳定系数ψ曲线由四段实线组成,各线段对应于该规定中的各项条款。
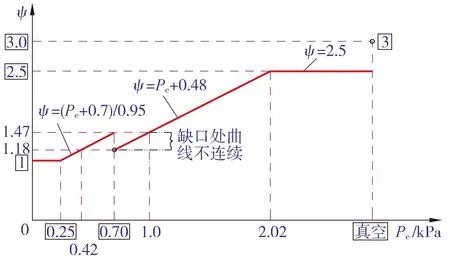
图3 标准对应的稳定系数ψ曲线
由图3可见,第二段曲线ψ=(Pe+0.7)/0.95 与第三段曲线ψ=Pe+0.48在其交界处断开,出现ψ=1.18~1.47 的缺口,此时两段曲线所对应的自变量Pe的取值范围分别为0.42 kPa≤Pe≤0.70 kPa及0.70 kPa 针对上述现象,提出如下修正建议: 1) 取消原B.3.2条第1款; 3) 原B.3.2条第4款改为“Pe大于1.2 kPa且小于或等于 6.90 MPa时,稳定系数ψ应取3.0”。 修正后稳定系数ψ对应的曲线见图4。 图4 修正后的稳定系数ψ曲线 以下仅针对自支撑式罐顶结构进行讨论。 罐顶外压公式(系由球壳弹性小挠度理论得到)为 (7) 故球壳(光面拱顶)板厚计算公式为 (8) (9) (10) (11) 取不同的外压稳定安全系数,则会得到不同的公式表达式。现将标准中关于罐顶计算公式及其对应的m取值汇总于表1。 表1 GB 50341—2014关于固定顶的计算公式及对应的外压稳定安全系数汇总 各时期立式圆筒形储罐固定顶外压稳定安全系数m的取值是不同的,其表现形式为罐顶计算公式的不同。现按时间先后顺序将锥顶(无肋)、光面拱顶及带肋拱顶三种结构类型的m的取值情况与对应的计算公式汇总成表2。 从表2中可以看到,锥顶的稳定系数经历了27→24→19.36的调整过程(由高到低),光面拱顶的稳定系数则恰恰相反,由最初的12提高到目前的19.36/24,但带肋拱顶的稳定系数m=12却一直没有变化,显然是不合理的。 表2 各时期固定顶外压稳定安全系数m取值情况及其计算公式汇总 注:表内计算公式中无Et项的,系按Et=2.0×105MPa得到的公式。 对于带肋锥顶,无论常压(Pe≤0.25 kPa)还是外压(Pe>0.25 kPa),为与不带肋锥顶一致,均取m=19.36并代入式(11),得到带肋锥顶许用外载荷计算公式 (12) 对于常压(Pe≤0.25 kPa)带肋拱顶,为与光面拱顶一致,取m=19.36(并取R=Rs)代入式(9),得到常压带肋拱顶许用外载荷计算公式 (13) 对于外压(Pe>0.25 kPa)带肋拱顶,为与光面拱顶一致,取m=24(并取R=Rs)代入式(9),得到外压带肋拱顶许用外载荷计算公式 (14) 符号说明: p——罐壁所受的压力,kPa; F——罐壁承受的内力[作用于抗压(拉)环有效面积上],N; σs、σs'——分别为Q235系列及除Q235系列外其他材料的屈服强度,MPa; Ae——罐顶与罐壁连接处有效面积A在扣除材料负偏差与腐蚀裕量之后的面积,mm2; Pi1——将罐顶板及其上的附件顶起需要的内压力,kPa; Pi2——Pi1之后压力继续上升直至计算破坏压力时的内压增量,kPa; m——罐壁外压稳定安全系数,无量纲; te——罐壁或罐顶板的有效厚度,mm; tn——罐顶板的名义厚度,mm; R——球壳顶曲率半径或锥顶在其与罐顶包边角钢连接点的曲率半径,m; [T]——罐顶许用外载荷,kPa; P——罐顶计算(设计)外载荷, CD130A2—84中采用的符号,kg/m2; P0——罐顶计算(设计)外载荷,SH 3046—92中采用的符号,Pa; [Pcr]——罐顶许用外载荷,CD130A2—84中采用的符号,kg/m2; [P]——罐顶许用外载荷,SH 3046—92与GB 50341—2014中采用的符号,单位分别为kg/m2及kPa。 其余符号说明同GB 50341—2014。7.2 B.3.2条规定的修正建议
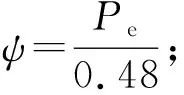
8 关于罐顶外压稳定安全系数的讨论及带肋拱顶计算公式的修改建议
8.1 外压稳定计算公式来源
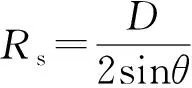
8.2 罐顶外压稳定安全系数m

8.3 罐顶外压稳定安全系数m值的调整变动史

8.4 带肋罐顶许用外载荷计算公式的调整建议