超高压压缩机气缸联结螺栓疲劳寿命预测
余德建,陈 晔
(南京工业大学 机械与动力工程学院,江苏 南京 211816)
某石化公司超高压乙烯生产装置使用的二次压缩机工作压力为117~310 MPa。该装置运行过程中,压缩机二级气缸上一高强度M80联结螺栓(螺栓材质 4340,规格M80×4 mm)的螺帽与法兰连接处,即螺纹啮合第一圈的位置发生了断裂。为保障装置安全,1根螺栓发生断裂就需一次性更换全部螺栓,而该类超高压压缩机均为进口设备,由此产生的费用极高。为对该设备的诊断与维护提供可靠依据,并提高产品经济性,准确评估剩余螺栓的寿命就极为重要。
国内外学者对螺栓联结结构的螺栓承载、应力分布及其疲劳寿命预测进行了许多理论计算和数值模拟研究。Bouzid A H等[1]对联结结构的螺栓垫片应力分布和螺栓载荷变化进行了研究,提出了一种预测螺栓载荷变化的方法。Esmaeili F等[2]通过试验和数值模拟的方法研究了双搭接简单接头和混合接头这2种不同接头形式对疲劳寿命的影响。数值模拟和试验结果表明,增大螺栓夹紧力可以提高试件的疲劳寿命。Chakherlou T N等[3]通过数值模拟对疲劳裂纹萌生和疲劳裂纹扩展寿命进行了估算研究,并将预测的疲劳寿命与疲劳试验测试结果进行了比较。结果表明,在采用数值模拟预测的总疲劳寿命与疲劳试验测试结果之间有很好的一致性,同时也对影响疲劳裂纹萌生和疲劳裂纹扩展寿命的因素进行了研究。杜静等[4]在研究风力发电机主轴疲劳的过程中将雨流循环计数法与线性累积损伤理论相结合,形成了一种新的主轴疲劳损伤计算方法,对于利用疲劳累积损伤理论对相关疲劳特性进行分析提供了一种新的途径与方法。陈沪等[5]完成了对超高压压缩机二段出口螺栓的疲劳寿命预测,为利用螺栓的裂纹扩展速率及临界裂纹尺寸估算螺栓的疲劳寿命提供了宝贵经验。随着理论知识的日趋成熟,在通过经验公式校核计算螺栓强度,对螺栓疲劳寿命进行预测等方面已经积累了大量经验。随着有限元技术的发展,目前对于螺栓联结结构的相关研究大多借助这一方法。李晓斌[6]应用有限元分析软件对钢轨接头螺栓螺纹建立接触对进行接触分析,得到应力集中现象主要发生在螺纹根部,螺母与钢轨夹板接触处第一圈螺纹根部应力最大。李会勋等[7]利用ANSYS对螺栓预紧力的施加方法进行研究,提出采用预紧力单元法可以很好地模拟螺栓预紧力单元的作用。周昌玉等[8]对压缩机螺栓联结结构的二维轴对称模型进行了研究,并对其疲劳寿命进行了分析,指出一定范围内增大预紧力可延长螺栓的寿命。杜洪奎[9]通过材料疲劳寿命方程回归有限元计算,应用局部应力应变法对螺栓试样疲劳寿命进行了预测,该方法的实用性及螺栓有限元计算结果的精确性也通过螺栓试样的疲劳试验得到了验证。
目前,有关缺口因素对压缩机螺栓联结结构疲劳寿命影响的研究较少。螺纹的存在会使螺栓局部危险部位产生应力集中,造成疲劳强度下降,更易发生疲劳破坏。文中从宏观、微观两方面对该超高压压缩机断裂螺栓断口进行分析,确定螺栓断裂原因,应用有限元软件ABAQUS对螺栓联结结构进行非线性接触分析,采用局部应力应变法进行疲劳寿命预测,并对剩余未断裂螺栓服役寿命进行评估。
1 螺栓断裂原因分析
1.1 断口宏观分析
现场取样的断裂螺栓典型宏观断口形貌见图1。由图1可见,断口底部表面光滑平整,断口上清晰可见贝纹线花样。该贝纹线在凹坑心部位置附近汇合,表明裂纹源位于螺栓圆周附近,且具有多源性(启裂源A和启裂源B)。启裂源B为主扩展断口,覆盖整个断口面。多源疲劳断裂断口的裂纹扩展区在不同的平面间相连接,且在连接处形成疲劳台阶或折纹。螺栓最终产生瞬断,瞬断区上形成45°剪切唇。螺栓断口总体上分为疲劳源区、疲劳裂纹扩展区和疲劳瞬断区,具有典型的疲劳断口特征,属于疲劳断裂。

图1 断裂螺栓典型宏观断口形貌
进一步对启裂源A、B进行观察分析,发现在螺栓断口取样过程中启裂源A处有撞击痕迹,启裂区形貌遭到破坏,不符合金相分析的条件。而启裂源B断口保存完整,可作为主要分析断口。
1.2 断口微观金相分析
采用扫描电镜对螺栓断口启裂源B的金相磨片进行观察,发现螺牙根部完好,未见裂纹,可知启裂源B的启裂位置不在螺牙根部。不同放大倍数下断裂螺栓螺牙表面区域金相照片见图2。由图2可以看出,螺栓螺牙为滚压成型,满足高强度螺栓的成型技术条件,裂纹启裂在齿合端面的顶端。螺牙表面呈现不平整状,说明表面存在一定的屈服变形区。

图2 不同放大倍数下断裂螺栓螺牙表面区域金相照片
从图3所示的断裂螺栓断口电镜扫描照片中未发现腐蚀迹象,可排除腐蚀的影响。从断裂螺栓断口疲劳裂纹扩展区电镜扫描照片(图4)可以清晰看到有疲劳裂纹扩展辉纹的存在,并且该疲劳辉纹由塑性撕裂峰组成,间距约10μm,具有典型的高周疲劳断口特征。

图3 断裂螺栓断口电镜扫描照片(60×)

图4 断裂螺栓断口疲劳辉纹电镜扫描照片(1 000×)
从螺栓断口宏观分析及微观金相分析可确定,该螺栓系因长期服役,在交变循环载荷作用下发生的低应力高周疲劳断裂,螺栓承受的是高载荷拉-拉疲劳应力,其疲劳辉纹由塑性撕裂峰组成。
2 螺栓疲劳寿命预测方法分析
2.1 名义应力应变法
名义应力应变法理论认为,对于相同材料制成的任意构件,只要应力集中系数相同,载荷谱相同,则疲劳寿命相同。由于名义应力应变法以构件的名义应力和应力集中系数为参考系数,因此应用该法估算构件的疲劳寿命时,首先需要找到应力集中部位的等效应力最大点,即确定构件中的疲劳危险部位,求出危险部位的名义应力和应力集中系数,再根据结构的载荷谱求出该部位的名义应力谱,最后根据材料的S-N曲线,应用疲劳累积损伤理论,计算出危险部位的疲劳寿命。名义应力应变法原理简单,理论成熟,工程应用广泛,但其基本假设与疲劳机理不符。相关试验表明,金属材料的疲劳是疲劳源附近材料反复塑性变形的结果,名义应力应变法未考虑缺口根部局部塑性累积的影响因素[10]。
2.2 局部应力应变法
局部应力应变法克服了名义应力应变法的缺陷,是一种比较成熟的估算疲劳裂纹形成寿命的方法。该方法的假设是,若同种材料构件危险部位的最大应力应变历程与光滑试样相同,则二者的疲劳寿命相同。控制参数为局部应力应变。应用该方法估算疲劳寿命时,首先确定危险部位的名义应力谱,再利用有限元法等计算出局部应力应变谱,查看当前应力水平下的应变寿命曲线,利用疲劳累加损伤理论,求出疲劳寿命。局部应力应变法在低周疲劳失效问题的分析和计算方面优势显著。在考虑构件表面加工和尺寸因素的影响,对应变寿命方程进行修正后,局部应力应变法可推广应用于高周疲劳寿命的估算,且计算精度较高[11-13]。
2.3 应力场强法
应力场强法理论认为,结构件中存在的缺口是工程结构的薄弱环节。无论是在静载、动载还是疲劳载荷下,结构强度都取决于缺口强度。若缺口根部应力场强度的历程与光滑试件应力场强度的历程相同,则二者具有相同的疲劳寿命[14-15]。应力场强法改善了名义应力应变法的缺陷,而且关注了应力梯度、尺寸效应等影响因素。但其发展时间较短,尚不成熟,很难应用于工程实际。
从疲劳机理以及工程实际应用难度综合考虑,采用局部应力应变法对文中压缩机联结螺栓的疲劳寿命进行预测。
3 螺栓联结结构非线性接触有限元分析
3.1 轴对称建模与网格划分
压缩机法兰和螺栓联接结构三维几何模型见图5。为便于计算,对螺栓联接结构模型进行了适当简化。由于螺纹升角小于4°,对应力集中程度的影响可以忽略不计,因此在建模过程中不考虑升角因素,对称建模。图5中的法兰截取的是实际压缩机结构中螺栓周围的局部区域,由于分析重点主要集中在螺纹接触部分,并不影响法兰的变形与受力,因此这种简化是合理的。

图5 压缩机法兰和螺栓联结结构三维几何模型
螺栓联结结构的载荷与实体模型均为轴对称,可以建立二维轴对称模型进行有限元计算。螺栓预紧力与工作载荷均为轴向拉伸载荷,计算时只取对称面一侧进行计算即可。螺栓联结结构轴对称有限元计算模型见图6。

图6 螺栓联结结构轴对称有限元计算模型
对有限元计算模型进行适当切分,采用结构化网格划分技术对模型进行网格划分,网格类型为CPS4R,见图7。为保证计算精度,对可能出现应力集中的螺纹接触部位的网格进行了适当加密 (网格数为62 419,网格节点数为249 676),见图8。

图7 螺栓联结结构有限元计算模型网格划分

图8 螺栓联结结构有限元计算模型螺纹连接部位局部网格加密
3.2 边界条件
根据螺栓联结结构的实际情况施加边界条件。在对称轴上施加对称边界条件,整体限制联结结构y轴方向位移。由于法兰与填料盘与后续机体相联结,故在法兰外表面施加固支边界条件。
3.3 螺栓工作总载荷
螺栓的主要作用是将法兰、填料盘、气缸以及机体进行联结。对结构整体进行受力分析可知,螺栓所受载荷主要为气体力以及螺栓安装过程中的预紧力。因此分析工况主要有预紧力与最大气体力、预紧力与最小气体力这2种。螺栓和法兰之间的联结件均为弹性体,根据弹塑性力学,螺栓承受的总载荷并不是二者载荷之和,螺栓的受力关系属于超静定问题。根据静力平衡以及变形协调条件可以求得螺栓工作总载荷:
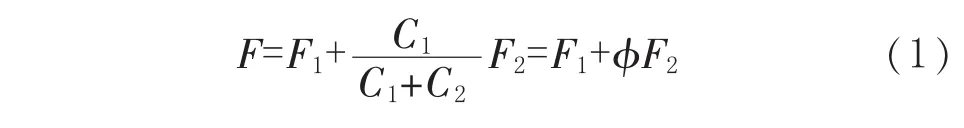
式中,F为螺栓工作总载荷,F1为螺栓所受预紧力,F2为螺栓所受工作载荷,N;C1为螺栓材料刚度,C2为联结件材料刚度,N/m;φ为螺栓材料相对刚度系数,根据螺栓实际联接情况和有关文献取φ =0.4[16]。
3.4 有限元计算结果
已知螺栓所受预紧力F1=256 000 N,螺栓所受最大气体力F2max=219 495.5 N、最小气体力F2min=82 841.85 N。 将联结螺栓总作用力等效加载到螺杆端面(螺杆直径 65 mm)。根据式(1)可知,在预紧力与最大气体力、预紧力与最小气体力工况条件下螺栓工作总载荷分别为352 798.2 N、298 136.74 N。计算结果表明,2种工况条件下,螺栓的应力、应变峰值均出现在内、外螺纹啮合的第一圈齿根底部圆角附近,而联结螺栓疲劳裂纹的萌生也始于第一牙根处,这与螺栓的实际断裂情况相符。计算得到的螺纹接触第一牙根处应力、应变结果见表1。

表1 螺纹连接第一牙根处应力和应变计算值
2种工况下联结螺栓应力、应变云图见图9和图10。由图9和图10可知,内、外螺纹啮合第一圈齿根圆角部位出现了明显的应力集中,最大应力已经接近联结螺栓材料的屈服强度σs(σs=659.85 MPa)。这与断口微观金相分析结果相符,验证了有限元计算结果的准确性。
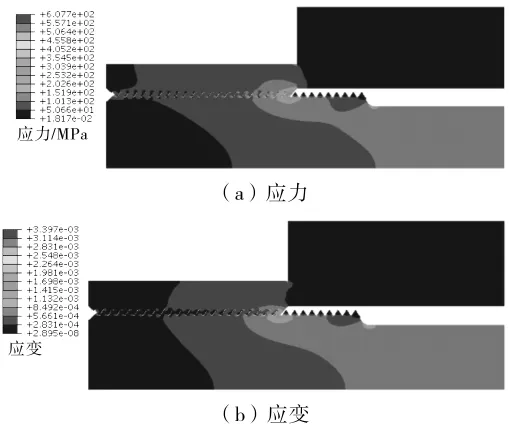
图9 预紧力与最大气体力工况下联结螺栓应力和应变云图
由图9和图10还可以看出,螺纹处受力极不均匀,内、外螺纹啮合的前3个螺纹承担了70%以上的载荷,其中1/3的载荷基本集中在第一圈螺纹上。这导致螺栓的疲劳强度出现一定程度的降低,更易发生疲劳破坏。
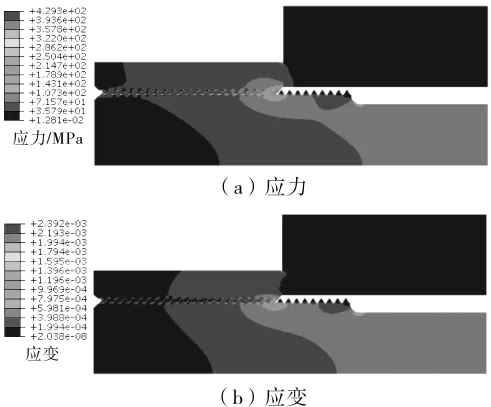
图10 预紧力与最小气体力工况下联结螺栓应力和应变云图
4 联结螺栓疲劳寿命预测
4.1 螺栓材料总应变寿命曲线
为测定联结螺栓的疲劳性能,进行了低周疲劳试验与高周疲劳试验,试验材料均直接取自库存的M80联结螺栓备件。按照GB/T 15248—2008《金属材料轴向等幅低循环疲劳试验法》[17]的要求加工试样,在R-9030电液伺服疲劳试验机上进行疲劳试验。进行低周疲劳试验时,试验方法参照GB/T 26077—2010《金属材料 疲劳试验 轴向应变控制方法》[18]执行,试验控制方法为应变控制,应变幅设置为0.43%~0.5%。进行高周疲劳试验时,试验方法参照GB/T 3075—2008《金属材料疲劳试验 轴向力控制方法》[19]执行,试验控制方法为载荷控制,载荷在19 870.62~32 358.40 N。应变与载荷控制均采用R=–1(R为应力对称循环系数)对称循环,加载波形为三角波,失效判据为试样断裂,对断口不在工作直径段范围内的试件作无效处理。
由Manson-Coffin应变寿命方程,总应变寿命曲线可分解为弹性应变寿命曲线和塑性应变寿命曲线。
总应变寿命关系:
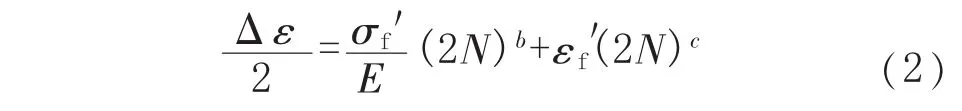
弹性应变寿命关系:

塑性应变寿命关系:
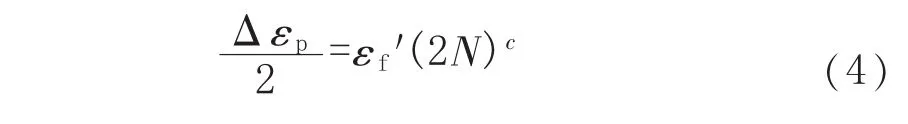
式(2)~式(4)中,Δε 为总应变,Δεe为弹性应变,Δεp为塑性应变,%;E 为弹性模量,MPa;N 为循环周次;σf′为疲劳强度系数,b为疲劳强度指数,εf′为疲劳塑性系数,c为疲劳塑性指数。
采用最小二乘法对低周疲劳及高周疲劳试验数据进行回归,可得 σf′=1 347、b=0.096 18、εf′=0.352、c=0.641 29,由此获得螺栓材料的总应变寿命曲线方程为:
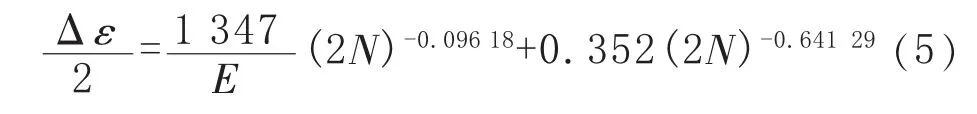
4.2 应用于高周疲劳的局部应力应变法
采用局部应力应变法估算螺栓寿命。考虑平均应力σm影响,总应变寿命曲线方程可改写为:

用此法估算高周疲劳寿命时,没有考虑表面粗糙度及尺寸因素,而这些因素对高周疲劳的影响不可忽视,会导致寿命估算出现较大偏差。为了使局部应力应变法能应用于高周疲劳分析,需考虑表面加工工序和尺寸因素的影响,对总应变寿命曲线方程中的b进行修正。
对式 (3),即弹性应变寿命关系方程两边分别取对数,在双对数坐标中变为直线方程 (图11)。图中弹性线1不考虑表面加工工序及尺寸对疲劳寿命的影响,而在考虑二者对疲劳寿命的影响后,疲劳极限从B点下移至C点,所以B点的纵坐标为 lg σ-1(σ-1为疲劳极限),C 点的纵坐标为 lg(εβσ-1),其中 ε 为尺寸系数,β 为表面加工系数。当单调加载,即2N=100=1时,表面加工工序及尺寸对疲劳寿命没有影响,所以A点没有下调。因此AB线的斜率即为疲劳强度指数b,AC线的斜率即为修正后的疲劳强度指数b′:


图11 高周疲劳寿命预测曲线
螺栓材料的弹性线方程为:
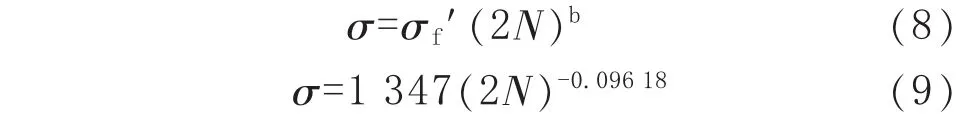
式(8)~式(9)中,σ 为循环应力,MPa。
将 2N=2×l07代入式(9)计算得 σ=267 MPa。而当N≥107后,金属材料到达其疲劳极限,此时疲劳极限 σ-1=σ=267 MPa。
低周疲劳与高周疲劳试样均直接取自螺栓,强度相同,所以可忽略尺寸因素对疲劳寿命的影响,取ε=1。查阅相关资料,螺栓表面经过精抛光等加工工序,故 β=0.95[20]。 将各参数代入式(7)可得修正后的 b′=0.099 32,将式(6)中的 b修正为b′,则总应变-寿命曲线方程变为:
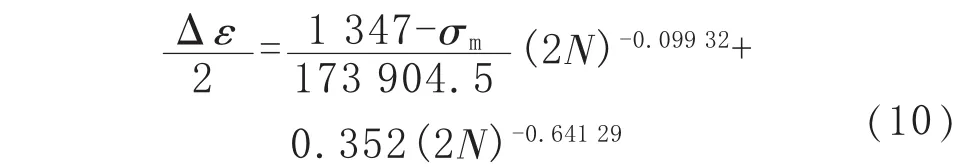
通过有限元计算获得其危险部位的局部应力应变谱后,即可通过式(10)预测构件疲劳寿命。
4.3 螺栓疲劳寿命预测
基于有限元计算结果,压缩机工作循环周期下螺栓平均应力 σm=518.5 MPa、Δε=1.005×10-3,经式(10)试差计算得 N=3.45×109,已知压缩机转速为200 r/min,每年服役360 d,因此该压缩机气缸联结螺栓疲劳寿命约为33.3 a。该超高压压缩机已经服役12 a,则剩余螺栓的服役年限约为21.3 a。
5 结语
基于超高压压缩机气缸联结螺栓断口的宏观检查及微观金相分析,明确了螺栓断裂属于低应力高周疲劳断裂,螺纹对螺栓形成缺口效应,第一圈齿根圆角附近出现应力集中,造成疲劳强度下降。螺栓有限元计算结果与微观金相分析结果相符,验证了有限元模型的准确性。采用局部应力应变法对螺栓疲劳寿命进行了预测,得到剩余未断裂螺栓的服役年限约为21.3 a。

