解密转盘游戏中的数学原理
◆湖北省赤壁市第一中学 谢雅兰 定 涵
一天上午,我们在路边看到这样一个游戏:摊贩前面放一张画有转盘的白纸,奖品摆在转盘的周围,有气球、铅笔、橡皮擦、钟表、溜冰鞋等,然后,摊贩拿出一副扑克牌让玩客任意抽出两张,并事先说好向哪个方向转,将抽出的两张扑克的数字相加(J、Q、K分别为11、12、13,A为1),得到数字n,就从n开始按照事先说好的方向转n-1步,转到哪个数字,那个数字前的奖品就归玩客。但唯有转到数字“1”的位置时,如图1,就必须付2元钱,转到其他位置都不必付钱。
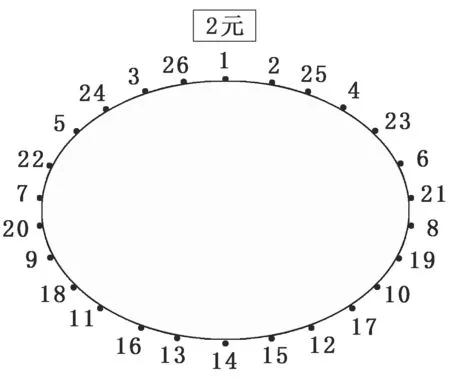
图1
通过一段时间的观察我们发现,所有参与游戏的玩客不是转到要付2元钱的位置即数字“1”,就是转到一些价值较小的奖品位置,而摆放钟表、溜冰鞋等贵重奖品的位置没有一个玩客转到过。
转盘上有26个位置,获奖的可能性有25/26,需要付2元钱的可能性只有1/26,怎会没有人中大奖呢?其中是不是有“机关”?我们对此展开了探究。
一、用观察法解密
1.过程
从转盘上的任何一个数字开始向左转或向右转,按照小摊贩设定的转法,转到付2元钱的位置所转过的最少步数恰好比这个数字少1(比如数字6,逆时针转5步到付2元钱的位置“1”,顺时针转5步到数字17)。因此,抽到的扑克数字之和无论是多少,或者左转或者右转,按照游戏规定的转法,只有两种结果,一个方向是转到付2元钱的位置;另一个方向是转到奇数的位置,绝对不会转到偶数的位置。
因为如果抽出的两张扑克牌的数字相加是奇数n,从这个数字开始转n-1(为偶数)步,相当于增加了“偶数”,奇数+偶数=奇数;如果抽出的两张扑克牌的数字相加是偶数n,从这个数字开始转n-1(为奇数)步,相当于增加了“奇数”,偶数+奇数=奇数。
我们观察转盘上奖品的分布发现,钟表、溜冰鞋这类价格高的奖品都放在偶数字前,而奇数字前只有气球、铅笔等价值较小的奖品。因为按照摊贩规定的游戏玩法,无论怎么转也转不到偶数字的位置,所以玩客就得不到价格高的奖品了。
2.结论
通过观察分析,我们发现了游戏的骗人“机关”:每转一次只有两种可能,要么转到付2元钱的位置,要么转到奇数字位置,玩客付2元钱与得到小奖品的概率都是1/2,相当于将每件价值几角钱的小物品用2元钱的价格卖出去。因此,玩客玩的次数越多,输的可能性就越大。
二、用归纳法解密
1.过程
因为n是两张扑克牌的数字之和,所以1 当n为奇数时,从n开始转n-1步得到的数要么是1,要么是其他奇数。其他的奇数有如下两种情形:当1<n≤13时,最终转到的奇数为2n-1;当13<n≤25时,最终转到的奇数为2n-27。观察转盘可知,若事先规定朝逆时针方向转,奇数n转n-1步后得到的数是奇数2n-1(1<n≤13)或奇数2n-27(13<n≤25),永远不可能转到位置“1”处;若事先规定朝顺时针方向转,奇数n转n-1步后得到的数都是付2元钱的位置“1”,不可能转到其他位置。 当n为偶数时,从n开始转n-1步得到的数要么是1,要么是其他奇数。其他的奇数也有如下两种情形:当2≤n≤14时,最终转到的奇数为29-2n;当16≤n≤26时,最终转到的奇数为55-2n。 观察转盘可知,若事先规定朝逆时针方向转,偶数n转n-1步后得到的数都是要付2元钱的位置“1”,不可能转到其他位置;若事先规定朝顺时针方向转,偶数n转n-1步后得到的数是奇数29-2n(2≤n≤14)或 奇 数55-2n(16≤n≤26 ),永远不可能转到位置“1”处。 注意:29-2n=55-2n-26,可见,两种情形的数学关系式有深刻的内在联系。 综合以上两种情况,对游戏转盘而言,若事先规定朝逆时针方向转,奇数n转n-1步后到达的数都是奇数2n-1(1<n≤13)或奇数2n-27(13<n≤25),偶数n转n-1步后到达的数都是位置“1”;若事先规定朝顺时针方向转,奇数n转n-1步后到达的数都是位置“1”,偶数n转n-1步后到达的数都是奇数29-2n(2≤n≤14)或奇数55-2n(16≤n≤26 )。 能否从数学的严密性要求出发,给出一般性的逻辑论证来得到结论?答案是肯定的。因为转盘可朝顺时针与逆时针两个方向旋转,所以将转盘上的数进行排列时,也应分顺时针方向排列与逆时针方向排列两种情况。 这里我们研究了逆时针方向排列的情况,顺时针方向排列的情况可采用相同的方法研究。 图2 转盘数字按逆时针方向排列 转盘的旋转过程中不变形,有些数在转动后会循环出现前面的数,所以这个数列是以1、26、3、24、5、22……25、2为基础循环排列的,所以当项数n超过26时,就有an=an-26。 根据数列的排列规律,我们发现项数n与对应项an之间有如下关系: 按照转盘规定的转法,当抽出两张扑克牌的和为an时,如果事先约定沿逆时针方向转,则转an-1步后,到达以上数列的第(n+an-1)项位置。 (1)当an为奇数时,由上面通项公式知an=n,从而n+an-1=n+n-1=2n-1(奇数)。再由上面通项公式得: 亦即奇数an(实际上就是奇数n),沿逆时针方向转an-1步后(即转n-1步后),到达以上数列的第(n+an-1)项位置,此位置对应的数是2n-1。 注意,以上结果是1<n≤13时的结果,当13<n≤25时,则2n-1>26,这时an=an-26。根据数列的排列规律 ,再根据通项公式,我们有: (2)当an是偶数时,则 偶数an沿逆时针方向转an-1步后,到达以上数列的第(n+an-1)项位置,此位置对应的数是: 亦即偶数an沿逆时针方向转an-1步后,到达要付2元钱的位置“1”处。 综合以上两种情况即得,若事先规定朝逆时针方向转,奇数n转n-1步后到达的数是奇数2n-1(1<n≤13)或奇数2n-27(13<n≤25),偶数n转n-1步后到达的数都是付2元钱的位置“1”。 如果沿顺时针方向排列转盘上的数,按照上述研究方法,很容易得出相应的结论。 我们研究了一种新玩法,玩客只赢不输:两张牌的点数之和是n,就从n开始按照事先说好的方向转n步(不是n-1步)。这种新玩法的结果是,无论如何都转不到要付2元钱的位置,即数字“1”处,但能转到偶数位置。玩客只要有耐心,就能分文不出地将小摊贩的奖品一扫而光。 然而,当我们向小摊贩说出改变游戏规则,按我们所说的玩法去玩时,小摊贩一口拒绝了。 发现转盘赢钱的“机关”后,我们又思考,能否设计一种玩法,让小摊贩每次都能赚2元钱,连小奖品都不给出一次?经过分析思考,我们发现这样的游戏玩法也是有的。但再贪的小摊贩也不会采用这种游戏玩法,因为如果玩客每次都输2元钱,一无所获,就会无人“上钩”。 通过对转盘“机关”的分析,我们更加意识到数学的重要性,只有认真学习数学知识,有一颗善用数学知识分析问题的大脑,才能让我们立于不败之地。赌博的花样层出不穷,如果我们对每一种赌博方式都能从数学的角度进行揭秘,相信社会将变得风清气正,人人都会在和谐的社会氛围中,凭自己勤劳的双手和智慧的大脑开创美好幸福的人生。 一句话,知识就是力量! 作者心声 经过观察分析,我们发现,所有设计的玩法中,小摊贩设计的玩法最“科学”,让玩客有失有得,虽有诱惑性与欺骗性,但能让玩客“无怨无悔”地自投罗网。看来设计游戏的小摊贩既有聪明的数学意识,又能抓住玩客的心理,让玩客乐在其中,哪怕受骗也不会找麻烦。 专家点评 数学源于生活,孩子们根据生活中看到的现象提炼出相应的数学问题,通过已有的知识水平和现实情境进行思考和推理,从而解密生活中的数学问题,充分体现了数学的生活价值。 从观察法出发,孩子们通过数学学习中重要的研究方法如归纳法、代数法进行研究,体现了其严密的科学思维方式;将数学知识与趣味游戏结合,体现了玩中学的思想;最后通过研究一种新的玩法,反映出他们具有很强的创新能力。
2.结论
三、用代数法解密
1.过程
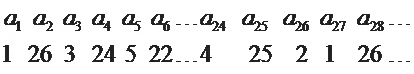


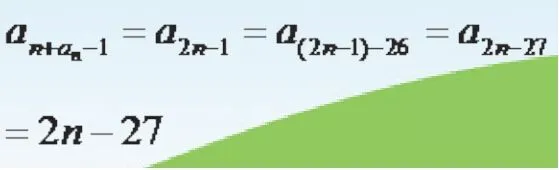


四、新玩法定输赢的奥秘


