基于递推公式的星载SAR高效反向定位算法

宫 俊, 秦 强, 张金强, 付朝伟, 郑广瑜

(1.上海无线电设备研究所,上海201109;2.上海目标识别与环境感知工程技术研究中心,上海201109)

0 引言

近年来,SAR反向定位在雷达立体摄影中得到了越来越多的应用[1-4]。利用雷达立体摄影技术提取目标高程,需要将SAR图像向叠加不同高程的先验数字高程模型(digital elevation model,DEM)投影,计算量非常大。因此,研究高效的SAR反向定位算法具有重要意义。

文献[5]提出了星载SAR定位常用的距离-多普勒模型,文献[6]首次给出了利用该模型进行反向定位的牛顿-拉普森迭代解法,以上两种算法运算速度较快,但是逐点迭代求解运算量较大。文献[7]利用有理函数模型(rational function model,RFM)拟合目标点经纬度、高程与其在SAR图像中坐标的关系。该算法在先验DEM上叠加不同高程,建立三维稀疏格网,并通过迭代算法求解格网点在SAR图像中的坐标;然后利用上述稀疏格网点估计RFM系数,将待反向定位点的经纬度和高程带入RFM模型,即可求解其在SAR图像中的坐标。文献[8]假设目标点在SAR图像中的距离和方位坐标可以用多项式拟合。在建立三维稀疏格网并求解格网点在SAR图像中的坐标的基础上,对每一格网点拟合其在SAR图像中的坐标与高程关系的多项式。然后通过双线性内插获取待反向定位点的多项式系数,将待反向定位点高程代入多项式,即可求取其在SAR图像中的坐标。与迭代算法对比,基于有理函数拟合和基于多项式拟合的算法在满足反向定位精度要求的同时,均可提高SAR反向定位效率,但是增加了三维格网建立、系数拟合或系数插值等繁琐操作。

通过分析距离方程和多普勒方程,提出了一种基于递推公式的星载SAR高效反向定位算法。该算法在建立的待反向定位二维格网中选择参考格网点,并通过迭代算法计算其在SAR图像中的坐标;然后利用两组递推公式计算待反向定位点在SAR图像中的坐标。该算法避免了三维格网的建立、系数拟合和插值等繁琐操作。

1 算法原理

1.1 星载SAR定位模型

星载SAR常用距离-多普勒模型进行目标定位[5,9]。时刻t雷达到目标的距离R(t)和目标多普勒fD(t)的计算公式分别为

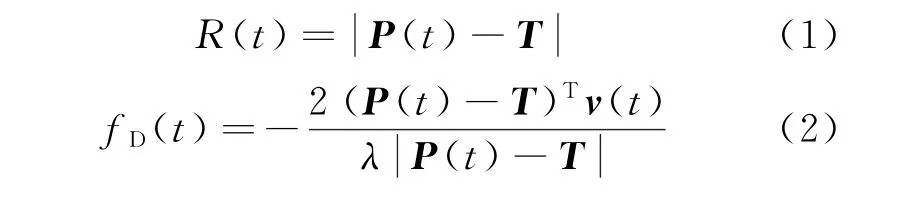
式中:P(t)=[Px(t),Py(t),Pz(t)]T表示时刻t卫星的位置矢量;T=[Tx,Ty,Tz]T表示目标点的三维空间位置矢量;v(t)=[vx(t),vy(t),vz(t)]T表示时刻t卫星的速度矢量;λ表示雷达工作波长。上述公式假定T,P(t)和v(t)均定义在世界大地坐标系(WGS-84)下。

反向定位是已知目标点的三维空间位置矢量T,确定其在SAR图像中的方位和距离坐标的过程。首先通过解算式(2)获取目标点i成像多普勒频率对应的时刻ti;然后通过式(1)计算时刻ti雷达到目标的距离R(ti);则目标点在SAR图像中的方位和距离坐标的计算公式为

式中:(ai,ri)表示ti时刻目标点i在SAR图像中的方位和距离二维坐标;t0表示SAR图像方位维第一个像素对应的方位时刻;fp为脉冲重复频率;R0表示图像距离维第一个像素对应的雷达斜距;fs表示信号采样频率;c表示光速。

1.2 定位模型求解

根据观测场景,在经纬度维划分二维均匀格网,格网点高程可以在先验DEM库中获取,如航天飞机雷达地形测绘库(SRTM DEM)。在建立的二维均匀格网中,按一定间隔选择参考格网点,并通过迭代算法计算其在SAR图像中的坐标。通过递推公式计算非参考格网点相对于参考格网点在SAR图像中的二维坐标增量,将该坐标增量与参考格网点在SAR图像中的二维坐标相加,即可求得非参考格网点在SAR图像中的二维坐标。

将式(1)和式(2)对目标点的三维空间位置矢量T求导,得到目标点在SAR图像中方位和距离二维坐标随其三维位置的变化公式为

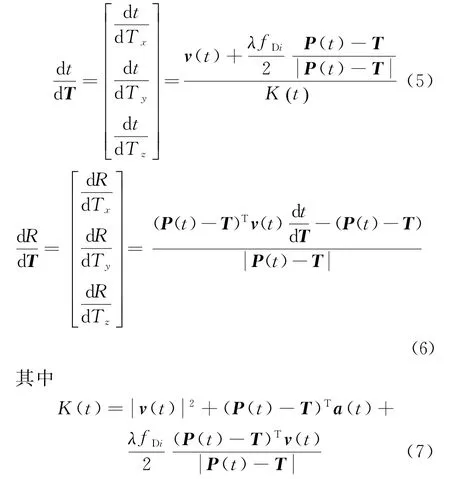
式中:fDi为第i个目标对应的多普勒频率;a(t)为时刻t卫星的加速度矢量。

设序号为k的非参考格网点T k和参考格网点Tref间的三维位置增量为ΔT k=T k-Tref,Tref在SAR图像中的二维坐标为(aref,rref),则T k在SAR图像中的二维坐标计算公式为

由于星载SAR斜距较大,在局部范围内目标点在SAR图像中的坐标随其三维位置变化的变化率近似恒定,因此在局部范围内可以使用同一参考格网点处的递推系数计算非参考格网点在SAR图像中的坐标。

1.3 处理流程

本文提出的反向定位算法的处理流程分为四步,如图1所示。

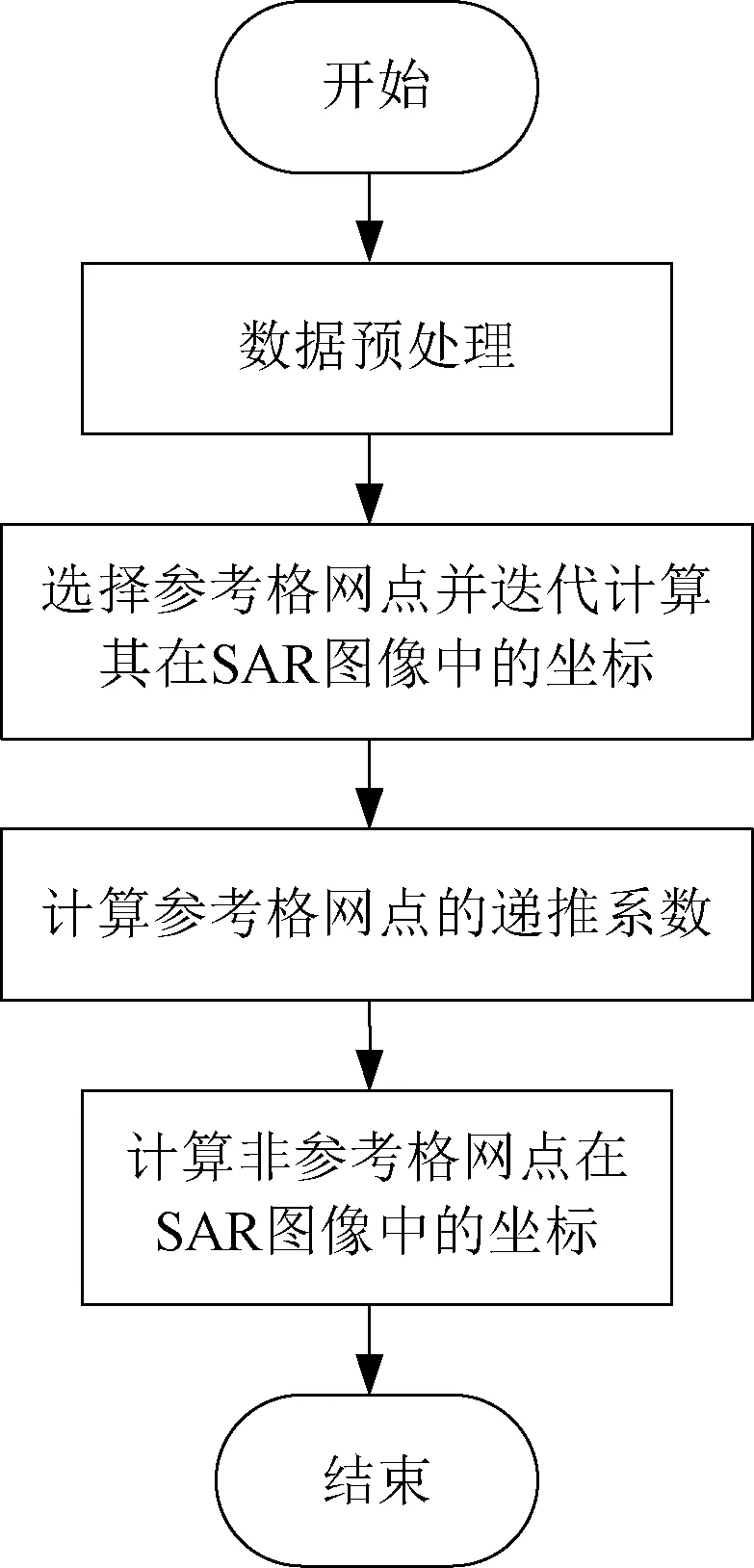
图1 本文方法处理流程图

步骤1,在大地坐标系下建立如图2所示的二维格网,格网点高程可以在先验DEM库(如SRTM DEM)中获取,并将格网点三维位置由大地坐标系转换到WGS-84坐标系。

步骤2,根据一定间隔选择参考格网点,利用迭代算法计算其在SAR图像中的坐标。

步骤3,利用式(5)和式(6)计算参考格网点的递推系数。

步骤4,利用最近参考格网点的递推系数计算非参考格网点在SAR图像中的坐标,输入参数为非参考格网点与参考格网点的三轴位置差。图2中虚线框内的非参考格网点在SAR图像中的坐标,利用中心参考格网点的递推系数进行计算。

图2 大地坐标系下二维格网示意图

2 实验验证

2.1 算法定位精度验证

利用仿真实验验证递推公式的有效性。主要的仿真参数为:信号采样频率164.83 MHz,脉冲重复频率2 633.39 MHz,场景近边斜距580.414 5 km。卫星轨道参数来源于TerraSAR-X系统。

在观测场景范围内选择六个均匀分布在正方体对角线上的目标点,如图3所示。其中T5相对于Tref的坐标位置为(200,200,200),单位为米。以迭代算法获取的各目标点在SAR图像中的坐标为参考,得到本文算法在成像多普勒频率为0 Hz和20 000 Hz情况下的反向定位误差,如图4所示。可知,本文算法在不同成像多普勒频率情况下的反向定位精度几乎相同;待反向定位点与参考点之间的三轴位置增量小于200 m时,反向定位精度优于0.007像素。

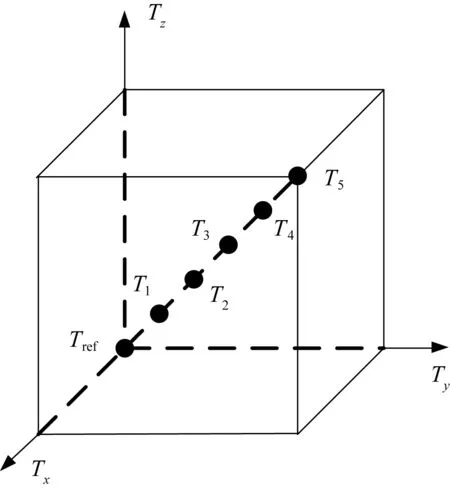
图3 参考点和待反向定位点示意图

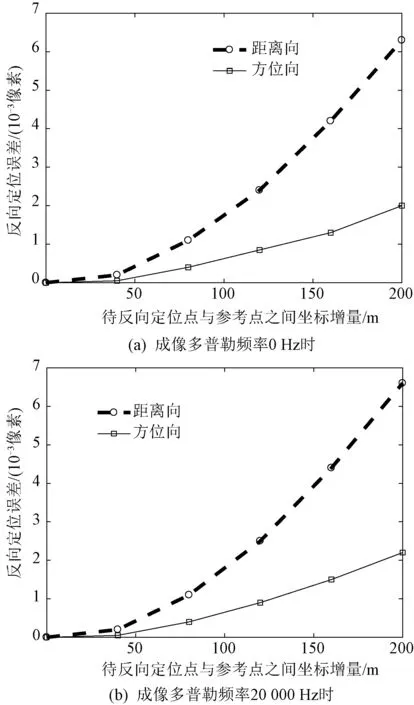
图4 递推公式精度验证

2.2 SAR图像反向定位验证

采用TerrSAR-X于2015年7月30日获取的西安秦岭区域的部分SAR图像验证算法的性能。

图5(a)为TerrSAR-X图像,图5(b)为观测场景对应的SRTM DEM,该区域平均高程1 500 m,图5(c)为参考格网点间隔为50像素×50像素时利用本文算法获取的地理编码结果。由图5(c)可以看出,由于雷达侧视成像以及地形变化引起的迎坡缩短、背坡拉长等几何畸变已得到校正。

图5 SAR反向定位结果

以迭代算法求解得到的反向定位结果作为参考,本文算法在参考格网点间隔分别为10像素×10像素、30像素×30像素和50像素×50像素时的反向定位误差统计结果如图6所示。

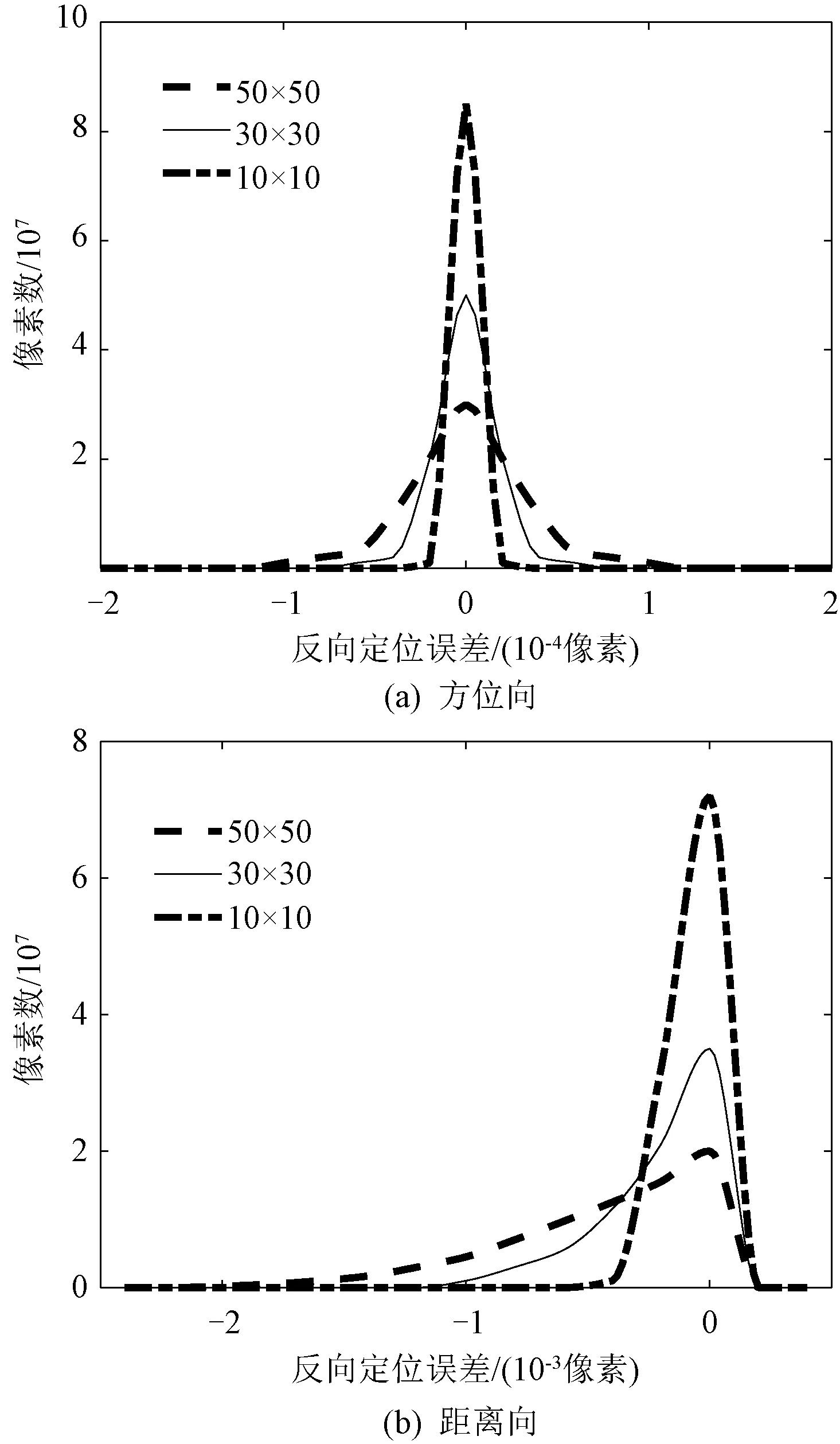
图6 本文算法反向定位误差统计结果

表1为迭代算法和本文算法在不同参考格网点间隔情况下的运算时间和最大反向定位误差统计结果。仿真运行环境为Intel Core i7 CPU,主频2.80 GHz,内存32 GB,程序语言为 Matlab。可知,随着参考格网点间隔的增大,本文算法在极大降低运算量的情况下保持了极高的精度。参考格网点间隔为50像素×50像素时,处理速度较迭代算法提升了约230倍,反向定位精度优于0.009像素,完全满足应用需求。

表1 不同算法处理性能对比

3 结论

本文提出了一种基于递推公式的星载SAR高效反向定位算法。该算法利用两组递推公式,计算待反向定位目标点相对于参考目标点在SAR图像中的坐标增量,将上述坐标增量与参考目标点在SAR图像中的坐标相加即可得到待反向定位目标点在SAR图像中的坐标。该算法避免了三维格网的建立、系数拟合和插值等繁琐操作。仿真和实测数据处理结果表明,该算法运算效率及精度较高,处理时间达到数十秒量级,误差达到千分之一像素量级。