基于静电场矢量的目标方位探测方法

李炜昕, 魏维伟, 涂 建, 瞿 宁

(1.上海无线电设备研究所,上海201109;2.上海市目标识别与环境感知工程技术研究中心,上海201109)

0 引言

静电探测[1-3]是通过感应目标与探测单元之间的静电场而获得目标静电信息的一种探测方法。基于被动式静电感应机理的探测系统具有结构简单、反隐身和抗电磁干扰能力强等优势,在气固两相流参数测量、航空发动机状态监测和空中飞行目标探测等领域具有广泛的应用前景[4-6]。

目前,国内外对静电目标方位探测开展了大量研究工作。中科院静电课题组[7]利用微机电系统(micro-electro-mechanical system,MEMS)电场敏感芯片获取大气电场信息,但该方法存在响应速度慢等缺点。北京理工大学静电探测课题组[8]采用平面圆阵被动式静电探测方法进行目标定位,理论上远距离定位精度可达(3～15)%,但在近距情况下方位解算误差大,适用于地面静电探测系统。德国的TRINKS等[1]利用正交静电探测阵列电极,提出基于阵列信号相位的测向算法,但是需要利用目标特征曲线中过零点的信息计算方位,适用于探测目标飞行轨迹。

针对静电探测系统小型化、高精度以及实时探测等特点,本文基于静电感应和静电平衡机理,分析静电场探测数学模型和电荷灵敏理论模型,建立阵列电极的静电场矢量探测数学模型。在此基础上,通过数学仿真和模拟试验等方法,验证静电场矢量探测的方位解算精度。

1 静电探测系统工作原理

静电探测系统是基于静电感应和静电平衡的原理进行设计的。处于电场中的孤立导体,外加电场将对导体中的自由电子产生力的作用,使电子逆着电场的方向运动,这种现象称为静电感应。静电感应可以使原来不带电的导体发生电荷的重新分布,并达到静电平衡状态,该过程通常都是在极短时间内完成的(约为10-19s)[9-11]。

静电感应探测原理如图1所示。设目标与感应电极的垂直距离为z,感应电极表面积为S,目标带电量为+Q,目标运动时间为t。目标以速度v从感应电极正上方通过,可以得到感应电流i。

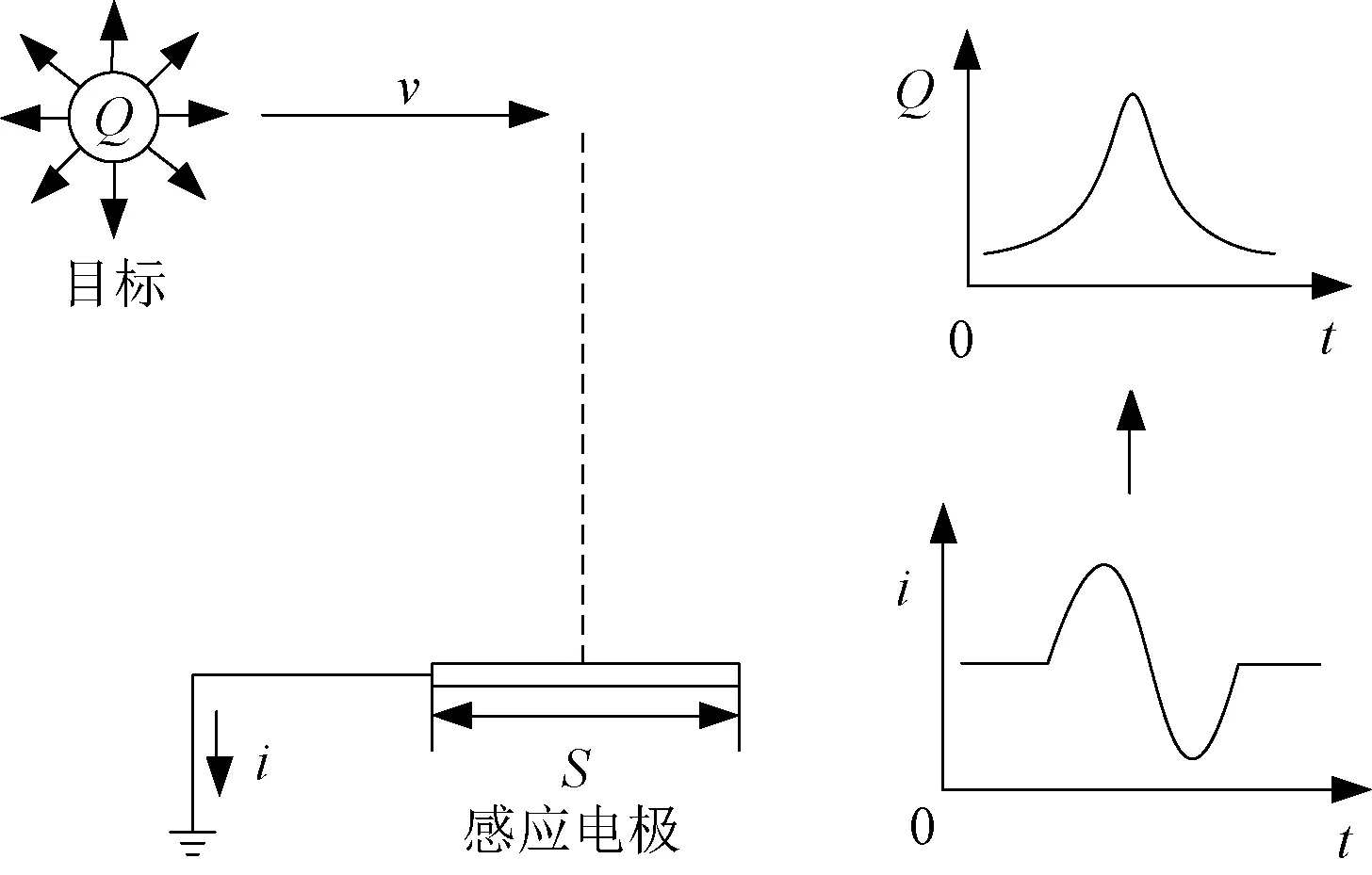
图1 静电感应探测原理

根据高斯定理,可得到感应电极表面的电荷密度

式中:ε0为真空绝对介电常数;εr为相对介电常数;Ean为感应电极表面垂直方向上的电场强度。

则感应电极表面的电荷密度为

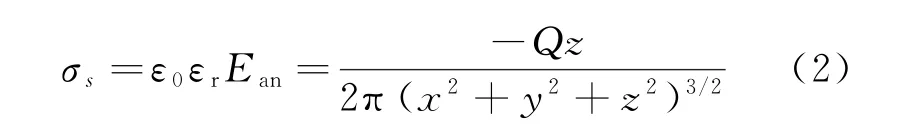
式中:x、y、z分别为目标相对于感应电极中心的位置坐标。

因此,感应电极靠近荷电目标一侧所带的异号电荷总量为

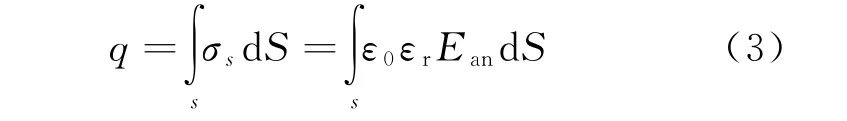
可得到探测电极所获取的感应电荷量

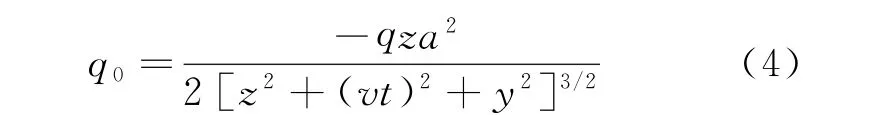
式中:a为圆形探测电极半径。

2 基于阵列电极的目标方位解算模型

在载体表面布设静电探测器感应电极阵列,建立目标方位解算模型,通过电极阵列得到空中目标静电场在探测器附近三维方向的感应分量,结合测向算法进行推算,可以得到空中目标的方位信息。拟采用静电场矢量方位解算方法,如图2所示。

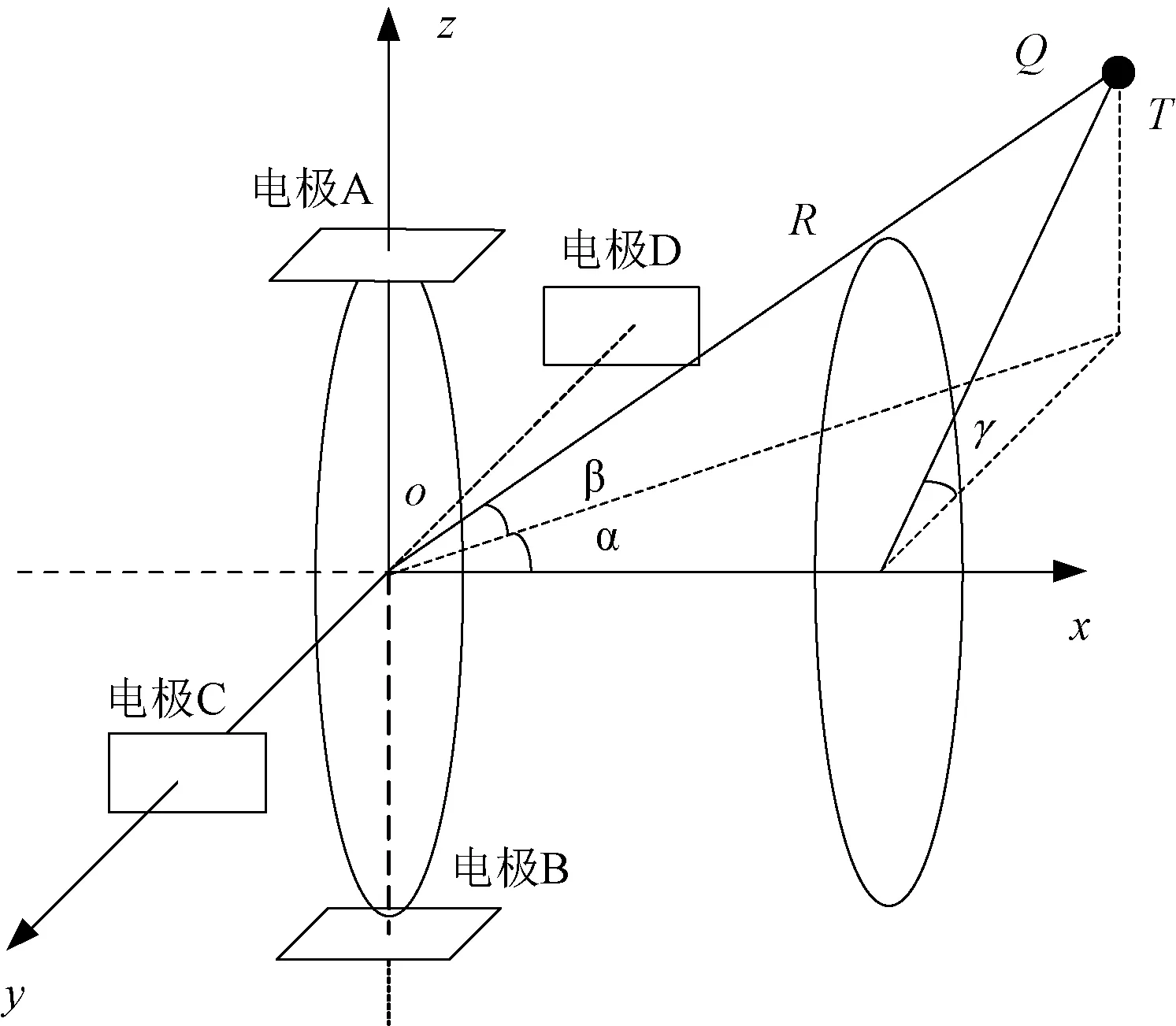
图2 静电目标方位解算算法示意图

将静电目标视为oxyz空间中的一个点电荷,其携带电量为Q;A、B和C、D为感应电极编号;γ为目标方位角。假设在某一时刻,目标处于T点,到坐标原点的距离为R,此时由于带电目标静电场的作用,两对静电感应电极极板间会产生不同的电势差。电场在极板对上产生的电势差分别记为UAB和UCD,表达式为

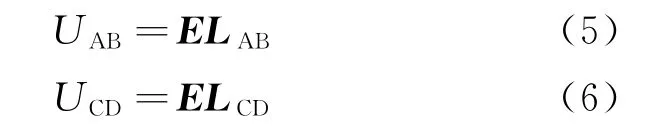
式中:E为目标电场强度矢量;LAB、LCD分别表示电极A、B和电极C、D两对平行极板间的距离矢量。结合电场强度公式和探测系统的几何关系,可获取极板对间的电势差分别为

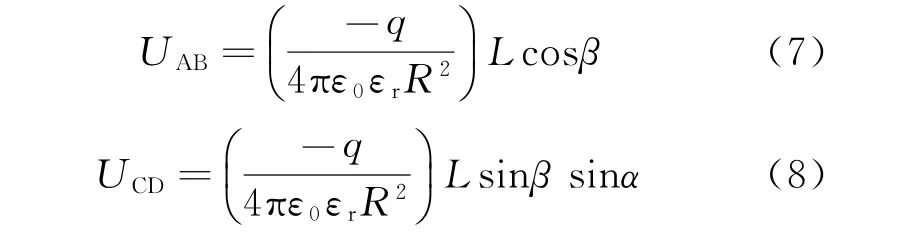
式中:α为偏航角;β为俯仰角;L为平行板电极间的距离。利用静电探测系统测得UAB和UCD,则可求出静电感应电极附近的电场强度,获取目标的脱靶方位信息为

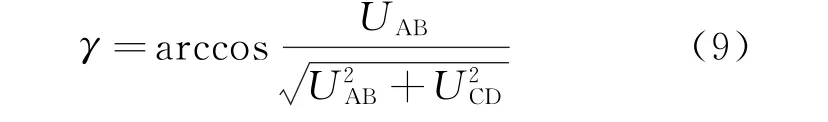
因此,采用正交平行布设的两组阵列感应电极,复合利用各个电极感应电荷幅值特征,就能够实现对任意时刻带电体方位的高精度解算。

3 数值计算分析

有限元方法适用于边界形状或边界条件复杂及介质分布复杂的问题的求解。由于这是一种数值解法,不受场域边界形状的限制,因此特别适用于求解本研究中涉及的静电场电荷分布问题。

3.1 数值计算模型

由于耦合模型需要进行静态和参数化动态分析,且形状相对复杂,简化为二维模型较困难,故采用三维模型进行电场仿真计算。利用有限元仿真分析软件Maxwell,建立数值计算模型。设目标为直径400 mm的铝质小球,沿z轴正方向运动;感应电极由两组铜板构成,厚度为1 mm,两组电极间距0.4 m,每组电极呈正交分布;求解域为矩形空气场;小球激励源为10 k V电压源,感应电极和导弹均设置为悬浮状态。

3.2 方位解算精度分析

对本文提出的静电目标方位解算算法的解算精度进行数值分析,静电目标方位探测的仿真模型定义如图3所示。四个感应电极呈正交方式分布于oyz平面,感应电极按逆时针方向顺序命名,即感应电极A、C、B、D;从弹头方向看,象限命名遵循传统数学象限规则。其中,静电目标位于坐标轴z轴负半轴上,初始位置与坐标原点相距8 m。

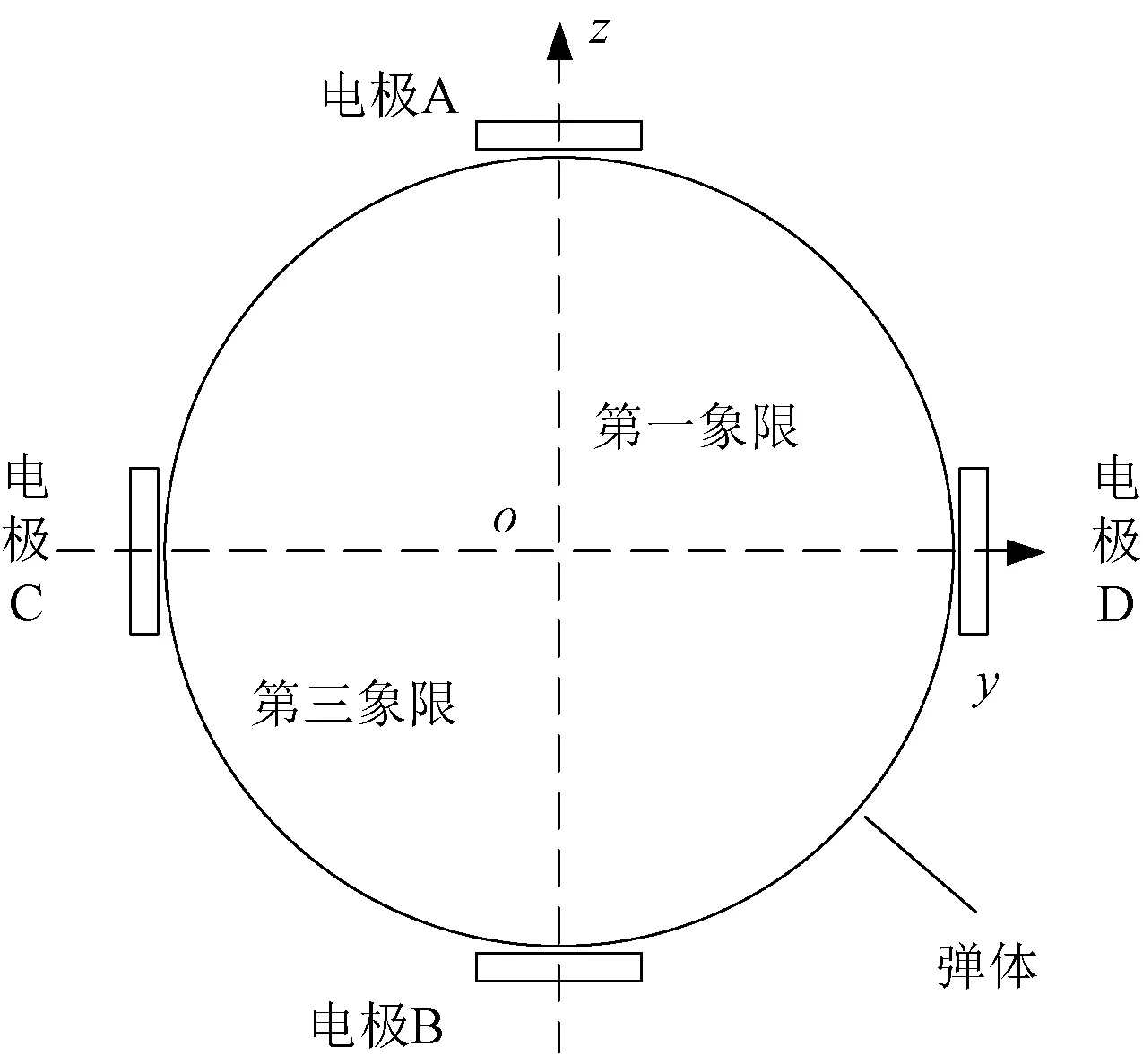
图3 仿真模型定义规则

进行参数化建模计算,利用麦克斯韦(Maxwell)场计算公式获取阵列感应电极的感应电荷总量,在1 000 m/s的交会速度条件下,感应电荷变化曲线如图4所示。从计算结果可以看出,在模拟弹目交会过程中,阵列中距离目标较近的电极感应电荷总量较大,在脱靶点电荷量达到最大值,感应电流为零;y轴方向的两对电极(电极C和电极D)由于在交会过程中与目标的距离始终相等,计算获取的感应电荷量变化曲线趋于一致;由于导弹弹体(结构)的影响,目标空间静电场分布会发生改变,导致感应电极电荷总量存在差异。

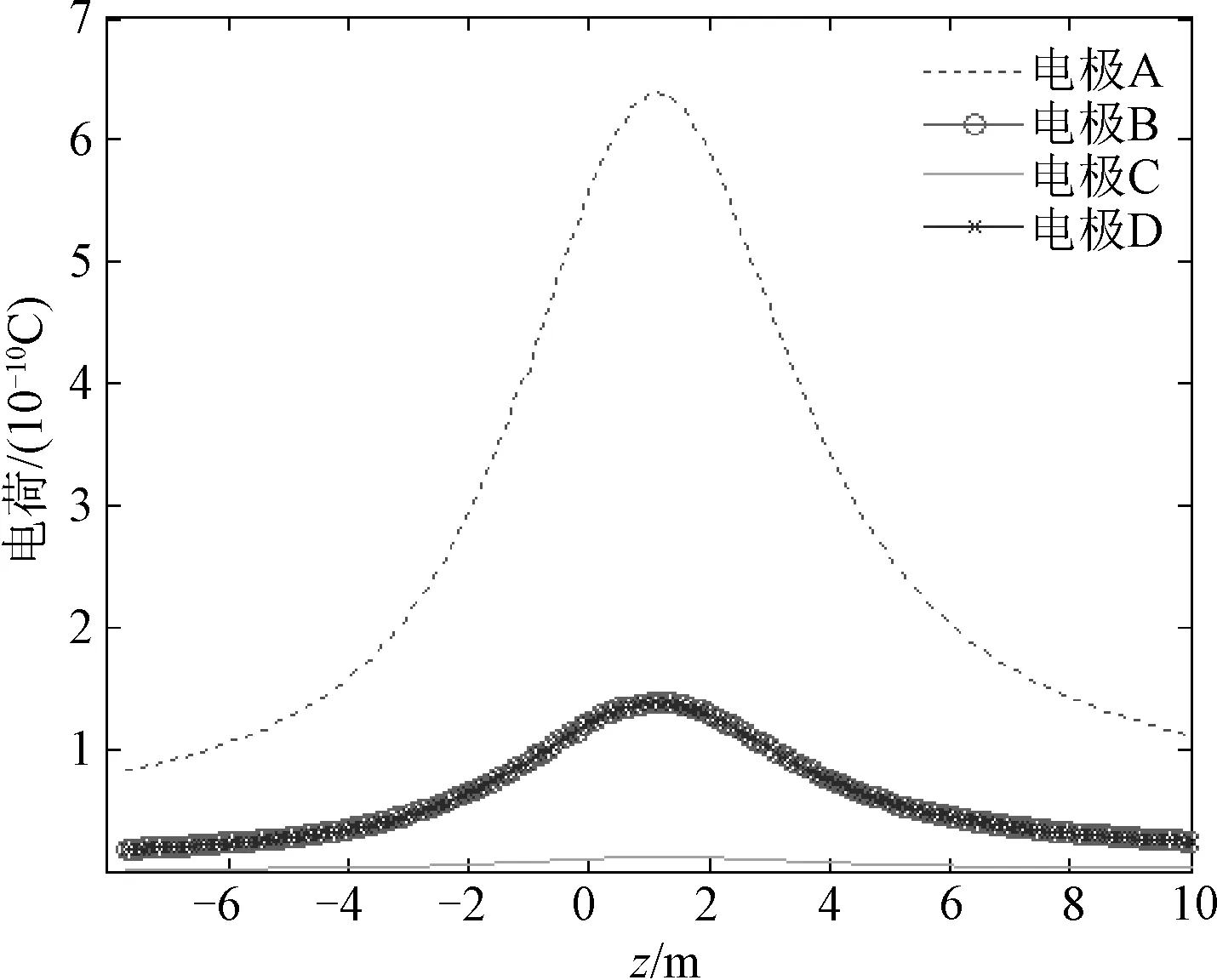
图4 感应电荷交会特征曲线

根据文中所建立的脱靶方位解算模型,对数值仿真获取的感应电荷数据进行数学计算,可以得到目标方位解算曲线,如图5所示。可知,方位角解算结果为90°,与弹目交会模拟过程一致。在有限元数值仿真交互过程中,由于采用了区域精细化网格划分方法,通过理论计算获取的目标静电场信息具有良好的一致性,因此理论计算获取的目标方位具有很好的探测精度。

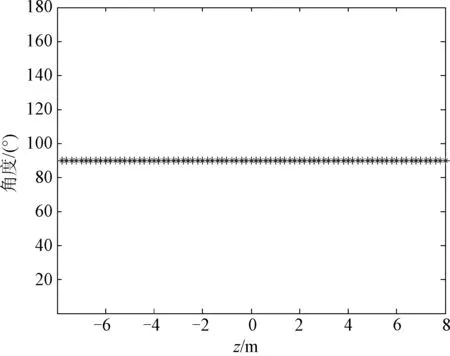
图5 目标方位解算曲线

4 试验验证

为验证静电探测理论和数值计算的正确性,进行了模拟弹目交会的准动态试验。试验系统由静电探测系统、目标模拟单元和数据采集系统构成,其中目标模拟单元由悬挂装置、静电目标、高压电缆、静电高压发生器和滑轨组成,如图6所示。试验目标为直径400 mm的球体,试验交会姿态为:脱靶量4.04 m,位置误差0.18 m,偏移0.04 m,交会平均速度13 m/s。

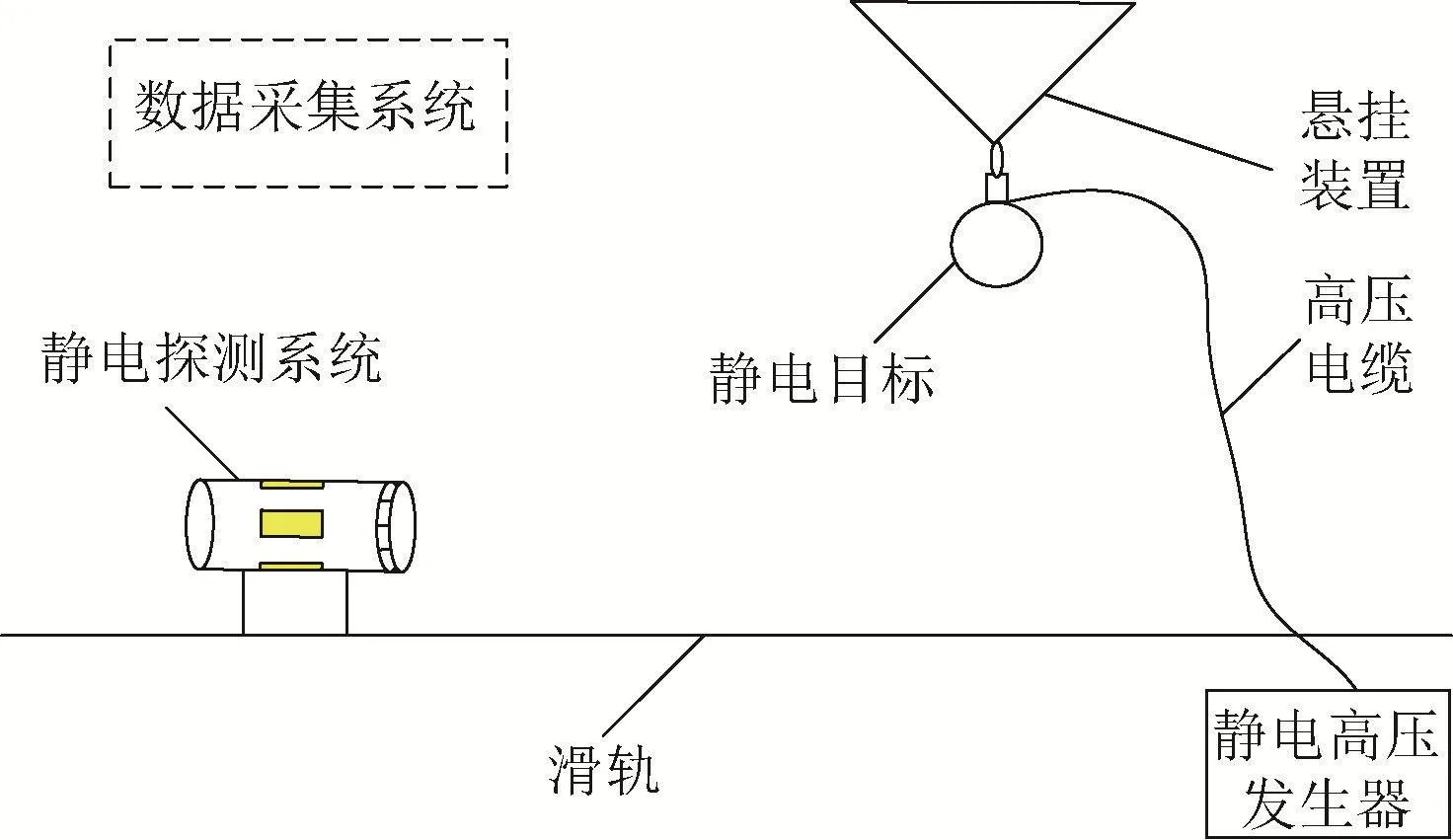
图6 试验装置

目标相对探测系统的方位角为135°,交会过程中静电探测系统输出信号如图7所示。目标在1.35 s时到达脱靶点,交会过程中相对速度逐渐增加,探测系统所获取的电压幅值逐渐增高。

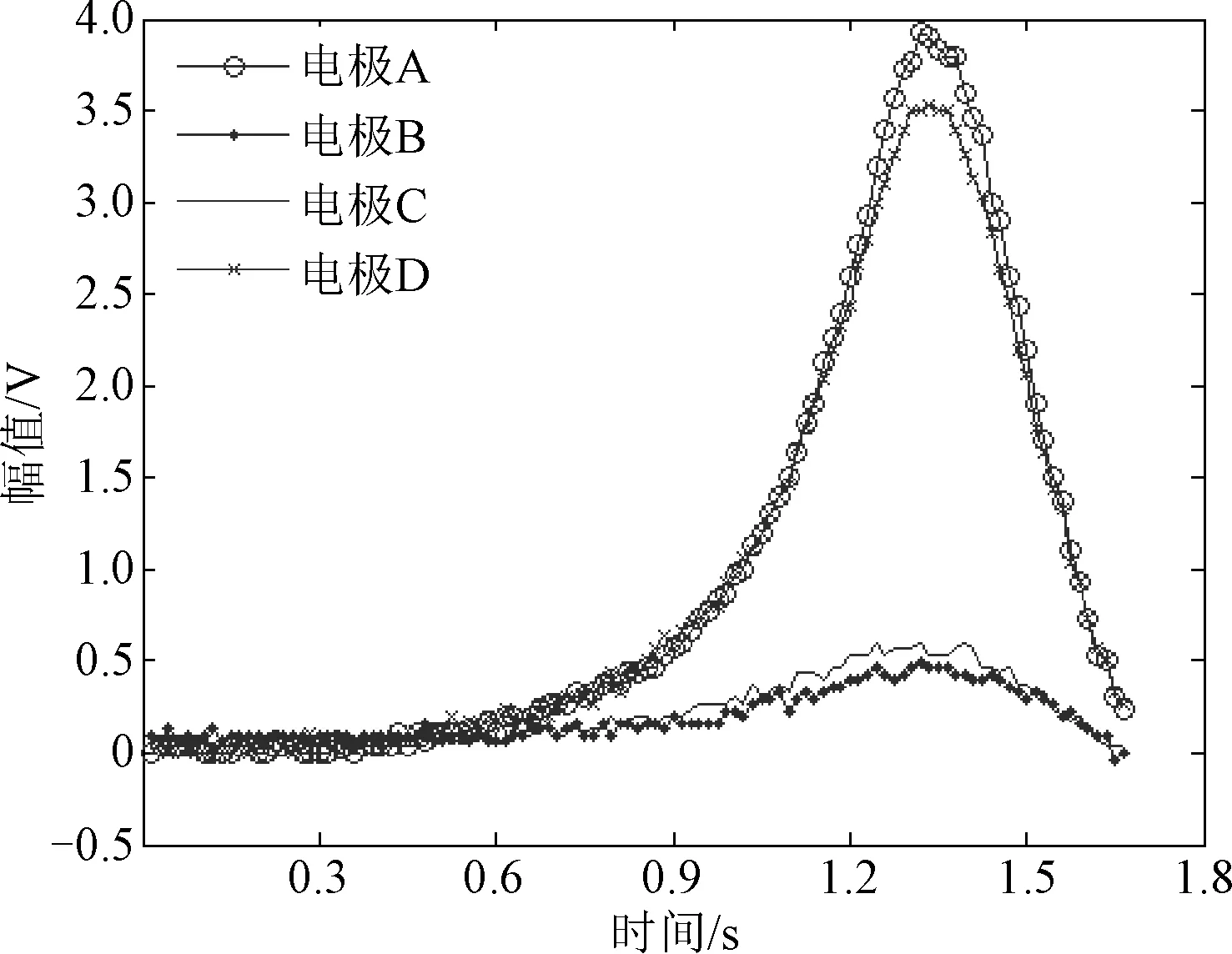
图7 静电探测系统输出信号

为验证探测系统角度解算精度,开展准动态外场试验。试验目标方位角范围为0°～360°,交会轨迹沿x轴方向。典型目标方位解算曲线如图8所示,解算数据如表1所示。

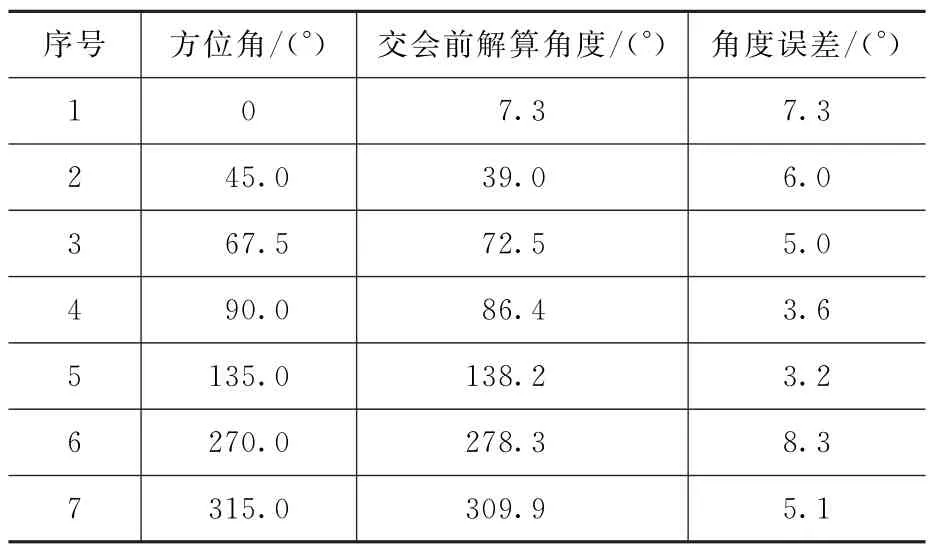
表1 目标方位解算数据

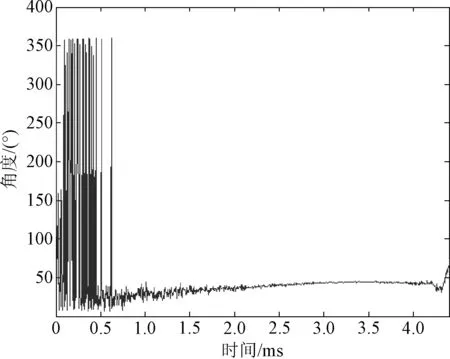
图8 目标方位解算曲线

由试验结果可知:

a)基于阵列电极的目标方位解算精度具有较好的一致性,角度误差的浮动较小;

b)在接近脱靶位置过程中所获取的角度精度较高,方位解算精度优于10°;

c)静电探测系统输出信号幅度越大,信干比越大,系统解算精度越高,误差越小;

d)方位解算精度稳定性有待提高,主要影响因素包括目标位置误差、静电探测系统误差和环境静电场随机误差等。

5 结论

基于静电感应和静电平衡机理,建立阵列电极的静电场矢量探测数学模型,通过数学仿真和模拟试验等方法,验证了静电场矢量探测的方位解算精度。理论分析和试验结果表明,在接近脱靶位置的过程中系统所获取的角度精度较高,方位解算精度优于10°。后续研究中可在自适应匹配滤波和数据处理优化算法等方面进行深入探讨,进一步提高静电探测系统方位解算精度。