多梁式钢-混组合连续梁桥横隔梁构造对整体性影响分析*

王栋威， 王祥真， 何余良， 肖景平

(1.绍兴文理学院 土木工程学院， 浙江 绍兴 312000；2.绍兴市交通工程质量安全监督站， 浙江 绍兴 312000；

计算多梁式组合桥梁结构中每片梁的荷载响应较复杂，设计中主要通过引入荷载横向分布概念将结构计算简化，将空间问题转化为平面问题。但荷载横向分布系数受到多种因素的影响。针对钢-混组合梁桥的荷载横向分布，聂建国等通过理论推导、试验及有限元分析，提出了主梁刚度、间距不相等的桥梁荷载横向分布系数计算方法；项贻强等考虑多梁式钢-混组合小箱梁桥界面滑移效应，对传统横向分布系数计算公式进行了修正；Razaqpur A. G.等采用非线性有限元方法研究了卡车荷载下砼非线性和钢筋弯曲对简支组合梁桥荷载分布的影响；Fatemi S.等比较了各国设计规范下曲率比、跨长、车道数、单元数等对荷载横向分布系数的影响；王柏璎采用模态参数法计算T梁桥和空心板桥的荷载横向分布，并分析了横隔梁设置、斜交角、主梁间距对简支梁桥荷载横向分布的影响。但现有研究较少涉及多梁式钢-混组合连续梁桥的横向分布。特别是近年来市政小跨径空心板桥改建工程增多，设计时简支组合梁的横向分布计算方法能否直接应用，二者间一些关键影响因素的影响程度是否一致，特别是横隔梁构造形式还有待研究。该文以现役连续钢-混组合梁桥为工程背景进行试验研究，探究现有横向分布计算方法能否用于连续钢-混组合梁桥，并采用文献[6]中基于荷载横向分布均匀性系数评价上部结构整体性的方法评价横隔梁构造形式对钢-混组合梁桥荷载横向分布的影响程度。

1 背景工程试验

绍兴市壶觞大桥改造工程的上部结构采用连续钢-混组合梁结构体系，跨径组合为(3×13+3×20+3×13) m。半幅桥面宽11.99 m，由6片钢梁组成，钢梁间布置小横梁，采用高强螺栓与钢梁连接，单孔设置3道小横梁(横梁间距4 m)加强其横向联系。钢主梁高0.65 m，钢筋砼桥面板为现场浇筑，设计标号C50。结构横断面见图1，表1为钢-混组合梁桥的计算参数。

图1桥梁结构横断面(单位：m)

选取13 m跨径进行试验。静载试验挠度测点设于钢梁底缘，测试断面沿纵桥向布置于Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ截面。采用全站仪观测结构竖向变位，以支点处挠度测值作为支座变位修正依据，按实测工况对以小横梁作为横隔梁构造的钢-混组合梁桥横向分布进行研究。车辆荷载纵横向布置及挠度测点布置见图2，实测车辆及棱镜布置见图3。

图2 加载车及挠度测点布置(单位：cm)

图3 试验现场

2 基准有限元模型

2.1 有限元方法

采用ABAQUS建立三维有限元模型。钢、砼均采用线弹性本构，砼弹性模量为34.5 GPa，泊松比为0.2；钢材弹性模量为206 GPa，泊松比为0.3。砼、钢主梁、小横梁均采用四节点减缩积分壳单元(S4R)，桥面板与主梁工字钢上缘采用Tie连接。钢主梁由工字钢与加劲肋组成，通过与小横梁采用Merge连接形成新的构件。实测桥梁整体模型、主梁与小横梁模型见图4。

图4 实测桥梁有限元模型

采用文献[1]中推导的公式计算横向分布系数，第i号梁的横向分布系数为：

(1)

式中：fi为i号梁的跨中挠度；n为加载车的列数。

2.2 有限元验证

该钢-混组合梁桥部分宽跨比远大于0.5，不采用刚性横梁法，而采用传统刚接梁法及考虑界面滑移的修正刚接梁法。美国AASHTO规范对于宽跨比没有具体要求，但其对设计车道数及内外梁的横向分布系数计算方法进行分类，并考虑了跨度、桥面板厚度、主梁刚度及间距的影响。通过理论计算及试验测试结果对有限元模型进行比较验证，试验测试值与有限元模型挠度值见图5，不同方法计算的各梁跨中横向分布系数见表2。

图5 桥梁跨中挠度值

从图5可看出：跨中试验测试值与模型计算值整体上吻合良好，最大误差出现在3#梁，为7.7%。说明修正后的三维有限元模型能较好地模拟多梁式组合梁桥在静力荷载作用下的受力性能。

从表2可看出：实测结果与有限元法计算结果非常接近，1#～5#梁的计算结果差值仅为0.2%～6.9%。由于试验实测结果精度较低，6#梁在实测工况下的挠度变化较小，未得到实测横向分布系数。刚接梁法与修正刚接梁法(见文献[2])的计算结果非常接近，1#～5#梁差值最大仅1%；6#梁差值相对较大，为8.3%。两种刚接梁法的计算结果与有限元法及实测结果也相差不大，最大差值出现在3#梁，与有限元法相比相差约9.3%，与实测结果相比相差约6.8%。文献[8]的计算结果最保守，与实测值相比相差约33.6%，与文献[10]的结论相似。

表2 各梁跨中横向分布系数计算结果

综上，界面滑移对这类桥型荷载横向分布的影响不大，考虑界面滑移的计算公式中，界面滑移产生的附加挠度仅占总挠度的0.3%，对于这类桥型的理论计算采用传统刚接梁法更方便快捷，简支组合梁的计算方法可直接应用于小跨径连续组合梁桥的横向分布设计。

3 横隔梁构造分析

钢-混组合梁桥的荷载横向分布与多个设计参数相关，横隔梁刚度对其有一定影响，但对连续组合梁桥横向分布的影响及程度还有待进一步研究。

以绍兴市壶觞大桥改造工程13 m跨径部分的钢-混组合梁为基准梁，对现有典型横隔梁构造形式(见图6)对其横向分布的影响进行分析。4种横隔梁构造适用于6片主梁间的连接，横隔梁的材料均采用Q345钢材。方式1中工字形横梁上下翼缘及腹板厚20 mm，宽300 mm，高450 mm。方式2中斜腹杆与弦杆均采用70 mm×7 mm角钢。方式三中K字形斜腹杆采用80 mm×5 mm方钢，下弦杆采用由4个80 mm×10 mm角钢拼接而成的箱形体，箱形体宽200mm、高280mm。方式四中上下弦杆采用T型钢TN147 mm×200 mm×12 mm×8 mm，斜腹杆采用100 mm×12 mm角钢。

图6 不同横隔梁构造形式示意图

对连续组合梁桥的中跨及边跨分别加载，评估连续组合梁桥边界条件对其横向分布的影响。单跨内每种横隔梁方式分别布置为3种形式：1) 跨内设置3道横隔梁构造(1/2L、1/4L处)。中跨加载下，方式1～4分别编号为M1-1、M2-1、M3-1、M4-1(字母区分加载位置，第一个数字区分构造方式，第二个数字区分横联数量)；边跨加载下，方式1～4分别编号为BM1-1、BM2-1、BM3-1、BM4-1。2) 跨内设置1道横隔梁构造(1/2L、1/4L处)。中跨加载下，方式1～4分别编号为M1-2、M2-2、M3-2、M4-2；边跨加载下，方式1～4分别编号为BM1-2、BM2-2、BM3-2、BM4-2。3) 跨内不设置横隔梁构造，中跨、边跨加载编号分别为M0和BM0。加载车荷载布置见图2，边跨加载顺桥向布置见图7。不同横隔梁构造在不同荷载布置形式下各梁跨中横向分布系数计算结果见图8。

图7 边跨加载车顺桥向布置(单位：cm)

图8 不同横隔梁构造下的横向分布系数

从图8可看出：1) 不同横隔梁构造在各种布置形式下的横向分布系数变化趋势相似，2#～6#梁总体呈下降趋势。2) 跨内无横隔梁时，无论是边跨还是中跨加载，跨中主梁间仅由砼板连接，在车辆荷载作用下2#梁的横向分布系数最大，且中跨加载时1#梁与其最大相差约9.5%。3) 跨内设置横隔梁时，横隔梁有利于主梁共同受力。中跨加载下，1#梁的横向分布系数不同程度增加(增加2.9%～9.7%)，2#、3#梁的横向分布系相应减少(分别减少3.0%～6.7%、3.5%～9.2%)；边跨加载下，与中跨相比少了一侧的连续段分担主梁内力，但4种横隔梁构造形式下，1#梁的横向分布系数最多仅增加6.5%，而2#、3#梁的横向分布系数相应减少(分别减少2.8%～7.2%、3.6%～9.2%)。说明不同横隔梁构造对这类桥型荷载横向分布系数有一定影响，但横隔梁数量的影响很小。

4 整体性评价

对于桥梁结构，提高其荷载沿横向分布的能力，增强其对不利荷载的协同抵抗性能，本质上是对桥梁结构整体性能的提高。采用文献[6]中荷载横向分布均匀性系数对桥梁上部结构整体性进行评价。各横隔梁构造形式下荷载横向分布均匀性系数按式(2)、(3)计算，计算结果见表3。

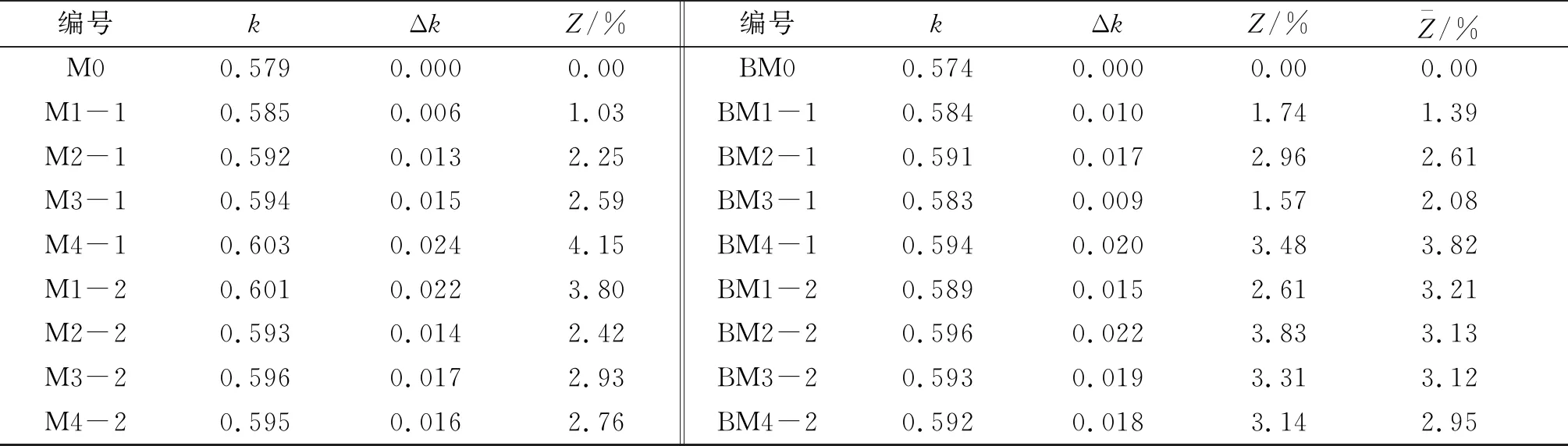
表3 各构造方式下荷载横向分布均匀性系数

(2)

Δk=k1-k2

(3)

式中：ηmax为横向分布系数最大值；μ为横向分布系数均值；k1为设置横隔梁构造时横向分布均匀性系数；k2为跨中无横隔梁构造时横向分布均匀性系数。

加载作用下荷载横向分布均匀性系数提高均值。

取同种构造方式横向分布均匀性系数均值来评价该构造形式对桥梁上部结构整体性的改善效果，结果如下：跨内设置3道横隔梁构造时，方式4>方式2>方式3>方式1；跨内设置1道横隔梁时，方式1>方式2>方式3>方式4。

5 结论

以绍兴市壶觞大桥改造工程上部结构为背景工程，通过试验和有限元方法对多梁式连续钢-混组合梁桥的横向分布计算方法及横隔梁构造形式对其整体性的影响进行分析，得出如下结论：

(1) 通过比较国内外横向分布系数计算方法，得出简支组合梁的横向分布计算方法可直接用于连续组合梁桥。

(2) 不同横隔梁构造形式对荷载横向分布系数有一定影响，但横隔梁数量的影响可忽略。跨内设置3道横隔梁时，方式4对于桥梁整体性的改善最好；跨内设置1道横隔梁时，方式1对于桥梁整体性的改善最大。