基于双层规划模型的改扩建高速公路收费站保通方案研究*

王凯， 李美玲， 张新， 冯琪， 贾庸， 冉晋

(1.山东高速股份有限公司， 山东 济南 250101；2.山东建筑大学 交通工程学院， 山东 济南 250101；

当前，高速公路改扩建主要采取全封闭施工、半封闭施工和不中断交通施工3种形式，其中不中断交通施工的高速公路改扩建工程采取“边通车，边施工”的建设模式，仅需对部分车辆借助周边路网进行分流，能最大限度降低对周边路网造成的压力和对当地经济产生的不利影响。

由于高速公路主线扩容，沿线收费站一般会对应采取原址扩建或新建扩容等方式来适应主线交通量。这就要求除新建收费站外，原有收费站要做好保通设计，在尽可能方便施工、保证质量的前提下，通过合理规划最大程度降低收费站车辆进出对施工区域造成的不利影响，同时减少交通量损失。目前，对改扩建高速公路收费站保通设计的研究大多集中在单一收费站的改扩建设计上，如文献[1-5]在通行能力分析、交通量预测等基础上对高速公路收费站改扩建方案提出了建议，文献[6-9]考虑工程建设区域经济社会、土地利用、土地环境影响、节能和社会评价等因素，针对收费站改扩建施工方案进行设计方法、施工技术、管理措施等相关研究。从高速公路改扩建工程全线出发，对工程沿线所有收费站的改扩建封闭施工时间进行统筹设计的研究还不多见。该文以改扩建高速公路全线收费站改扩建施工时间为切入点，基于决策者和使用者的双重需求构建双层规划模型，并将其应用于某改扩建高速公路收费站保通设计，通过模型求解得到最优改扩建高速公路收费站保通方案。

1 双重需求分析

研究改扩建高速公路收费站的最优保通方案，应以决策者和使用者的双重需求为考量，其中决策者指高速公路建设业主方(以改扩建项目管理办公室为代表)和施工方(以各标段施工承包方为代表)，使用者指改扩建工程沿线需要出入高速公路的所有车辆驾乘人员。决策者和使用者分布见图1。

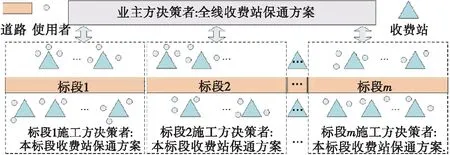
图1 决策者和使用者分布示意图

1.1 决策者需求

决策者分为总决策者和分决策者。总决策者为建设业主方，负责改扩建高速公路全线收费站保通设计的总体决策，其需求为改扩建工程总工期不受影响、因统筹发生的工程费用增幅最低、收费站流量损失最小等。分决策者为各标段的施工承包方，根据施工计划、机械配置和人员数量等进行本标段收费站保通设计的具体决策，其需求为收费站改扩建工期变化最小、施工工序基本不变、不增加额外的工程费用、保证施工安全等。

1.2 使用者需求

在高速公路改扩建期间，使用者因某处收费站封闭施工而需绕行其他收费站以达到出入高速公路的目的，其需求为绕路距离最短、绕行路线不拥堵、绕行费用增加最小、可绕行收费站不拥堵等。

2 问题描述

假设高速公路改扩建工程分为m个标段，每个标段有n个收费站，每个收费站使用者人数为k，收费站保通设计的决策见图2。

图2 收费站保通设计的决策示意图

决策者假设：1) 总决策者根据高速公路改扩建工程总工期和各标段实际施工进度等，决策全线m×n个收费站的封闭施工顺序和工期。2) 分决策者根据各自标段的施工进度、施工机械和人员配备等，决策各自标段范围内n个收费站的封闭施工顺序和工期。

使用者假设：1) 使用者根据所处位置与收费站的最短路程时间选择相应收费站出入，该路径称为时间最短路径。2) 当时间最短路径上的收费站因封闭施工关闭时，使用者可选择最近的相邻收费站绕行。3) 收费站封闭施工期间，使用者可选择不走高速公路，使用其他非高速道路。4) 使用者绕行仅考虑行程时间成本和燃油费用的增加。

其他假设：对于高速公路两侧对称分布的收费站，两侧同时施工时按照一个收费站考虑，两侧分别施工时按照两个收费站考虑，可在参数编号时明确。

3 双层规划模型构建及求解

3.1 模型建立

分别用m、n、k表示高速公路改扩建工程施工标段个数、各标段内收费站个数、各收费站车辆数的集合，均为正整数集合。施工标段和收费站统一编号，按照从小到大顺序排列(见图3)，例如图3中(m,2)表示标段m上的第2个收费站。

图3 高速公路改扩建工程沿线收费站编号示例

采用双层规划模型解决改扩建高速公路收费站保通问题。上层问题的目标函数和约束条件受决策者变量控制，同时依赖于下层目标的实现；下层问题的目标函数与决策条件受使用者变量控制，同时受上层决策的影响。

3.1.1 上层规划模型

对于决策者而言，因收费站封闭施工导致工程费用增幅最低、工期受影响程度最小、交通流量损失最小是其需求目标。据此从决策者角度建立上层规划模型如下：

(1)

(2)

式中：λij为第i个标段第j个收费站的关联参数，λij=1表示该收费站封闭施工，λij=0表示该收费站开放通行；m为标段个数；ni为第i个标段的收费站个数；Fi(Qj)为第i个标段第j个收费站增加的工程费用；Pi(Uj)为第i个标段第j个收费站因施工工期改变增加的费用；Sij为第i个标段第j个收费站损失交通流量的费用。

3.1.2 下层规划模型

对于使用者而言，因收费站封闭施工选择绕行增加的行程时间成本和燃油成本最小化为其需求目标。据此从使用者角度建立下层规划模型如下：

(3)

(4)

式中：S为收费站损失的交通流量；z为某收费站车型分类数；Dijl为第i个标段第j个收费站第l类车辆的通行费；pijl为第i个标段第j个收费站第l类车辆数选择其他路径的比例，由tijl和oijl两个参数决定；tijl、oijl分别为第i个标段第j个收费站第l类车辆增加的单位行程时间成本(元/h)和燃油成本(元/km)；kij为第i个标段第j个收费站的车辆总通行费。

3.2 模型求解

该研究属于双层线性规划(BLP)，其解集为各收费站封闭还是开放的不同组合，即λij是0或1的不同组合，属于有限离散型集合，记为集合A，任意一个可行解记为Ai。该模型可转化为单层线性规划问题进行求解，在有限非空的组合中寻优计算得到全局最优解。

理论上可采用穷举法求解该模型，即确定解集A的所有组成可行解，针对每个可行解标定各种参数，计算后比较确定最小目标值。但该方法会增加很多不必要的工作。因此，根据实际情况罗列有限可行解，并在可行解中标定参数寻找最优解，求解流程见图4。

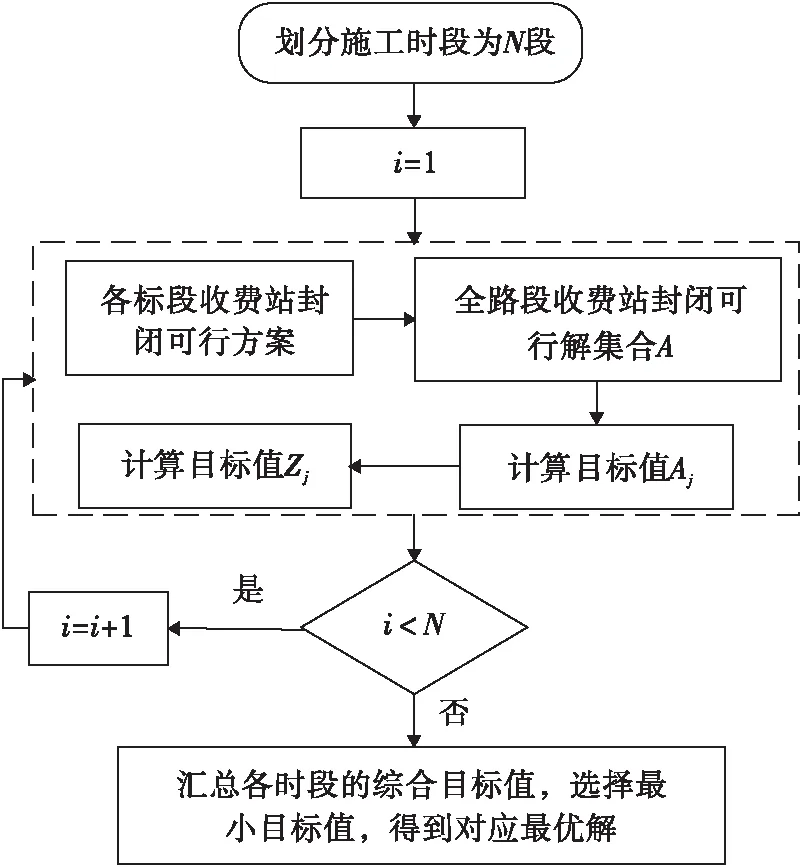
图4 最优解求解流程

4 模型应用

4.1 实例分析

某高速公路改扩建工程路线全长309.172 km，原为双向四车道，改扩建后为双向八车道，设计速度120 km/h。采用沿既有老路以“两侧拼宽为主、局部单侧或两侧分离加宽为辅”的加宽方式，标准路基宽度42 m，新建及加宽桥涵设计汽车荷载等级采用公路-Ⅰ级。

全线共分为6个标段，施工内容主要包括主线两侧拼宽、互通立交匝道改扩建、桥梁涵洞拼接及原有主线与互通立交匝道路基路面翻修、收费站房建和机电设施改造等。该高速公路收费站互通改造工程共涉及23处，其中新增收费站8处、原位扩建收费站7处、原位改建收费站3处、移位新建收费站5处。收费站序号、相邻最近收费站距离和入口流量见表1。

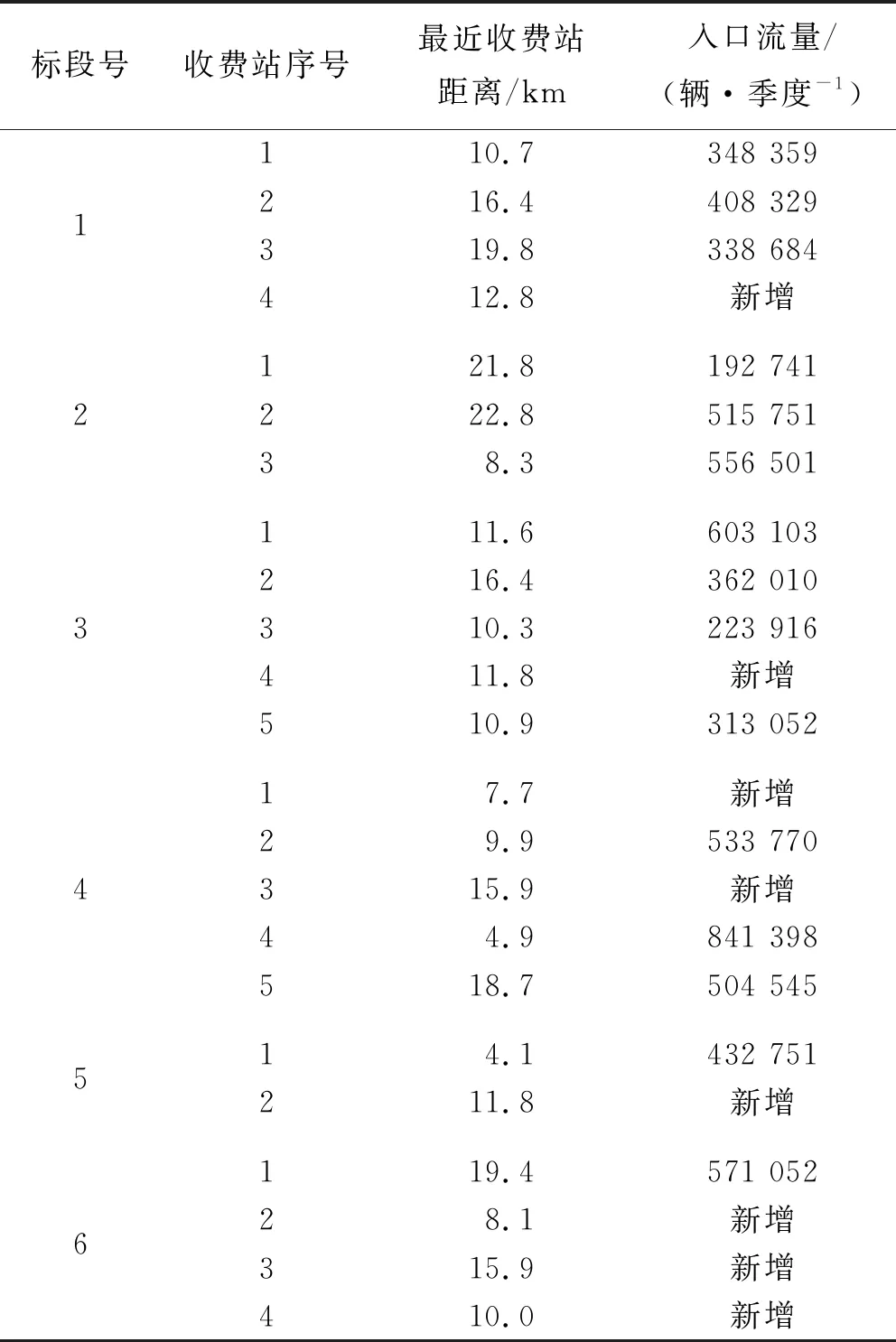
表1 某高速公路改扩建工程施工标段、收费站信息

4.2 实例求解

4.2.1 参数标定

该高速公路改扩建工程的施工标段数m为6个；各标段的收费站个数，n1为4个，n2为3个，n3为5个，n4为5个，n5为2个，n6为4个。Fi(Qj)和Pi(Uj)需根据收费站封闭或开放的具体工期安排，由各标段施工方进行工程和工期增加费用标定，如果施工人员和施工设备等足够而不产生额外工程费用，则其值均为零。

决策者统计每个收费站上季度的平均交通流量，确认不同类型车辆的可绕行路径，标定每条绕行路径的行程时间和燃油消耗作为阻抗，采用全有全无法在路径中进行比例分配，确定不同类型车辆选择非相邻收费站的车流比例，并计算对应收费站损失交通流量的费用Sij。

该高速公路改扩建期间限行五轴及以上大型车辆，故通行车型统计中没有五轴及以上大型车辆。为计算方便，把其他类型车辆按照收费标准换算为一类车的数量，当量车辆数见表1中入口流量。行程时间和油耗按照小汽车标准取值。

由于工程费用不改变，最优化问题可转化为损失流量最小，不需标定费用损失。

4.2.2 求解过程及结论

按照图4所示模型求解流程，将该高速公路改扩建施工划分为两个时段，即各标段承包方把工程分成两个施工时段来完成。各标段根据改扩建收费站数量的实际情况，选择一次封闭1、2或3个收费站进行施工。对于第一施工时段，由每个标段负责制定和上报收费站封闭施工方案，组合之后得到全线收费站保通可行解集A：

A=

借助MATLAB软件编程实现模型求解。通过计算，得到每个可行解对应的目标值Zj。所有目标值对比分析后表明全线第一施工时段收费站改扩建最优保通方案为A1：

A1=(1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,

0,1,0,1,0,1)

(5)

式(5)表明：相邻两个收费站不同时封闭施工即错时封闭施工的方案可使交通流量损失率最小，优于其他方案；且相邻标段施工时，服从总体布局才能达到全局最优。

同理，得到第二施工时段收费站改扩建最优保通方案为A2：

A2=(0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,

1,0,1,0,1,0)

(6)

式(6)表明：对第一施工时段确定开放的收费站在第二施工时段采取封闭施工可使交通流量损失率最小，达到最优解。

由此，得到该高速公路改扩建期间因收费站封闭施工导致的交通流量损失(见表2)。

表2 某高速公路改扩建工程收费站封闭期间车辆损失量

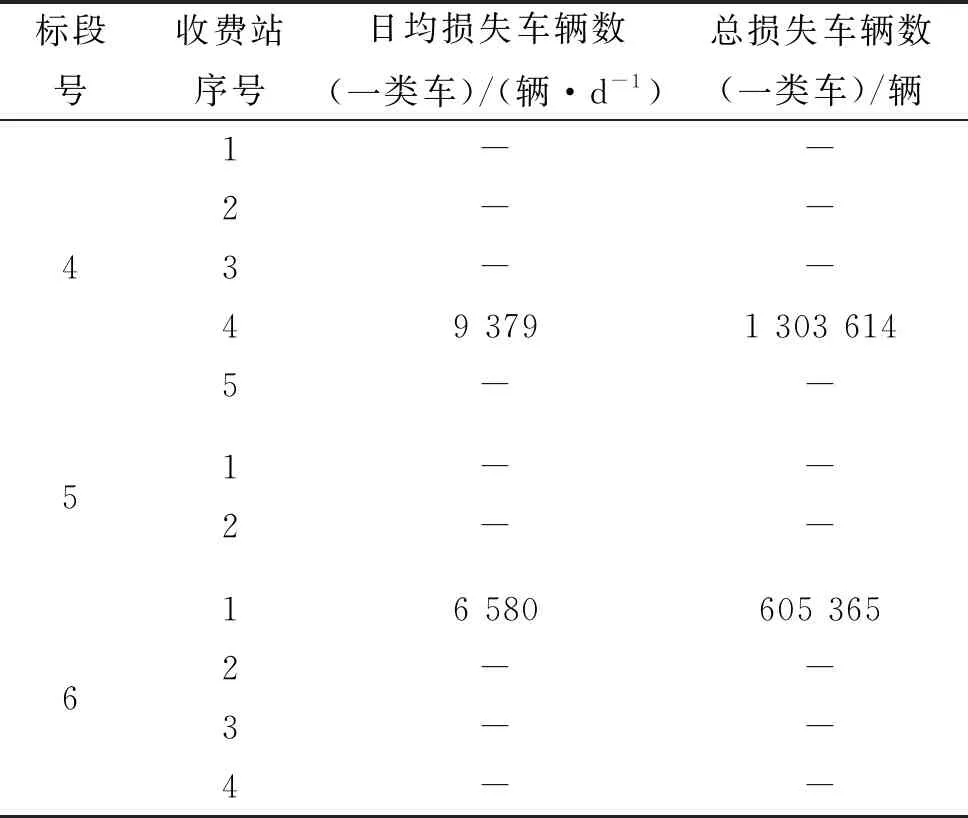
续表2

5 结语

在高速公路改扩建工程建设中，收费站改扩建是十分重要的施工项目之一，也是改扩建高速公路联系周边区域的关键节点，如何合理安排收费站改扩建的封闭施工顺序对于决策者和使用者均具有重大影响。从决策者和使用者的双重维度出发，分别考虑其不同需求构建双层规划理论模型，通过标定模型所需参数，将模型转化为有限解集的单层线性规划问题进行求解，可用于高速公路改扩建工程中收费站封闭施工最优保通方案确定。该方法具有通用性，但在实际应用中各种参数的标定是难点，不同工程差异很大，需根据具体情况确定。

高速公路改扩建期间对收费站的封闭施工需注意协调以下问题：一是收费站封闭施工应注重沿线区域经济发展的需要，确保改扩建工程沿线每个县(市)都具有出入高速公路的通行条件；二是收费站封闭施工期间，应避免道路使用者绕行距离过长；三是单个收费站封闭施工的期限要尽可能准确，最大程度满足土建、房建和机电施工计划的衔接，避免造成施工工序搭接不畅而影响改扩建工程总工期。