分数阶Buck-Boost变换器的建模与分析
谢玲玲,覃锐,刘斌,苏志鹏,宁康智,张伟斌
(广西大学 电气工程学院,广西 南宁 530004)
0 引言
开关变换器是开关电源的核心,电感和电容又是开关变换器中重要的电子器件,开关变换器的建模准确性也会影响到控制器设计性能的高低。目前,大部分DC-DC变换器建模都是用整数阶模型来描述,即变换器的电容和电感都被认为是整数阶。Westerlund指出电容和电感是分数阶的事实[1]。
由于电感和电容在本质上是分数阶,用分数阶微积分理论对DC-DC变换器进行建模与分析比整数阶更能准确描述变换器的特性。文献[2-4]用分数阶微积分来对电感电流连续导电模式(continuous current mode,CCM)、电感电流断续导电模式(disontinuous current mode,DCM)、电感电流伪连续导电模式(pseudo continuous conduction mode, PCCM)的Boost变换器进行建模与分析,研究结果表明,基于分数阶微积分理论建立的Boost变换器的分数阶模型与整数阶模型有着很大的差异,整数阶模型会导致建模的准确性降低。文献[5-6]用分数阶微积分理论分别对CCM、DCM的Buck变换器进行了分数阶数学模型和状态平均模型的建立与分析,学者用分数阶微积分理论对Buck变换器进行建模与稳定性分析和带有损耗滤波器的Buck变换器进行建模与控制[7-8],研究结果表明,利用分数阶微积分理论对Buck变换器进行建模与分析比用整数阶建模有更接近实际。目前存在多种关于分数阶的定义,不同的定义对变换器进行建模与分析存在误差,且根据这些定义难以给出系统整数阶的解析解。很多学者采用数值算法,如状态平均模型法、预矫正数值算法、Aomian分解法对分数阶系统进行求解与分析。由于分数阶数值算法在计算机软件仿真时占用较大的内存以及运算过程耗费较长时间,并且没有整数阶的解析表达式,难以从数学上直接得出结论。相对于数值解,等效小参量法(equivalent small parameter method, ESPM)的整数阶的解析解更加具有一般性,更能直观体现系统状态变量之间的联系,仿真运行速度快以及占用内存小,也可以对变换器的稳态特性进行分析。文献[9-10]采用ESPM分别对CCM和DCM的分数阶Boost变换器进行建模与稳态特性分析。用分数阶微积分对DC-DC变换器的建模主要在Buck和Boost变换器中,对Buck-Boost变换器研究较少,Buck-Boost变换器具有电压工作范围大、效率高等优点,广泛应用于计算机、航天和通讯等领域。
因此,文章以分数阶Buck-Boost变换器为研究对象,首先结合谐波平衡原理和ESPM,推导了电感电流和电容电压的稳态解析表达式,用稳态解析表达式对分数阶Buck-Boost变换器进行建模,解决了几种分数阶微积分定义在DC-DC变换器中适用性的问题。然后,对变换器的电感电流和电容电压的谐波成分进行提取和分析,研究了电感和电容分数阶阶数对各谐波阶次的影响,给出了变换器运行在CCM的判别条件。最后,在Simulink中搭建变换器的仿真模型,通过仿真验证了建模和理论分析的正确性。
1 CCM的分数阶Buck-Boost变换器数学模型
分数阶Buck-Boost变换器电路图如图1所示,图中,Vin是电源电压,δ(t)是开关函数,ST和SD是开关管,R是电路电阻,iL和vC分别是变换器的电感电流和电容电压,α和β分别是电感和电容的阶次。
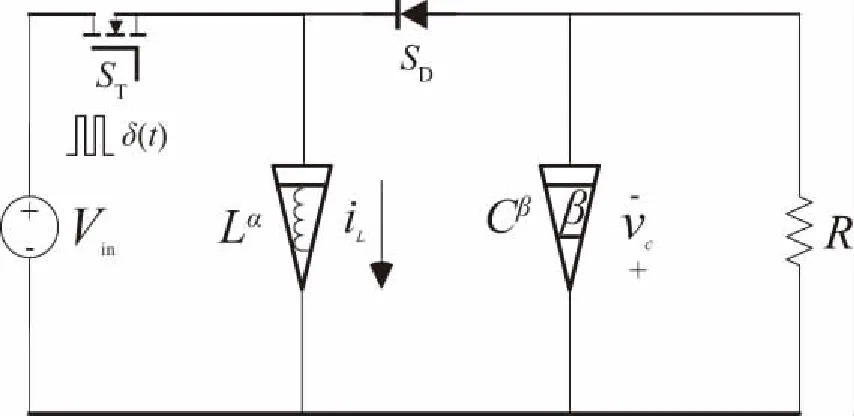
图1 分数阶Buck-Boost变换器电路图
分数阶电感电流和电容电压具有如下关系[11]:
(1)
当α和β都等于1时,式(1)为整数阶的表达式。
开关管ST和SD受到开关函数的控制,当开关管ST导通时,δ(t)=1。当开关管ST关断时,δ(t)=0。δ(t)可定义为
(2)
变换器运行在CCM时,分数阶Buck-Boost变换器在一个开关周期Ts内有两个工作模态:
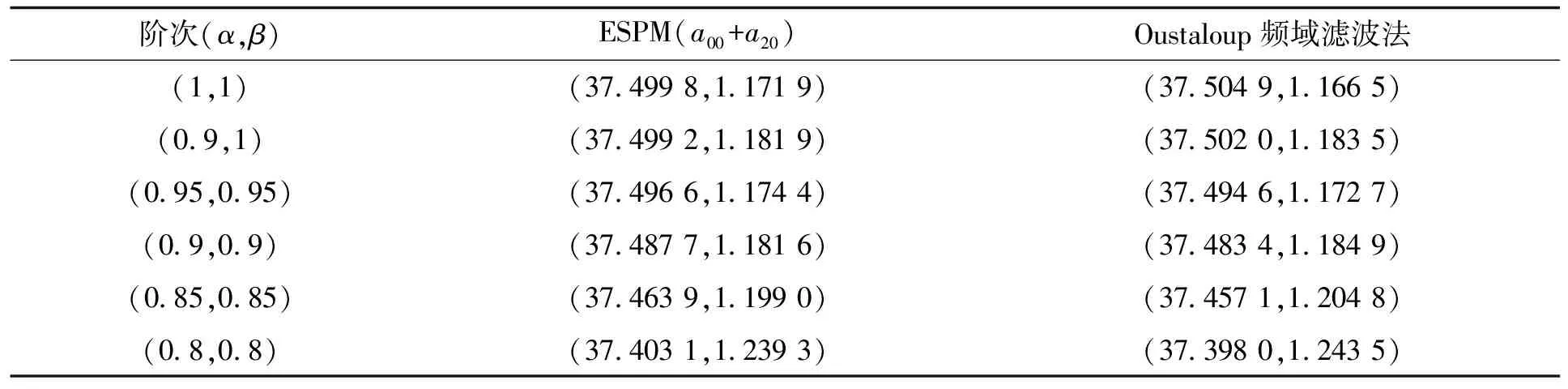
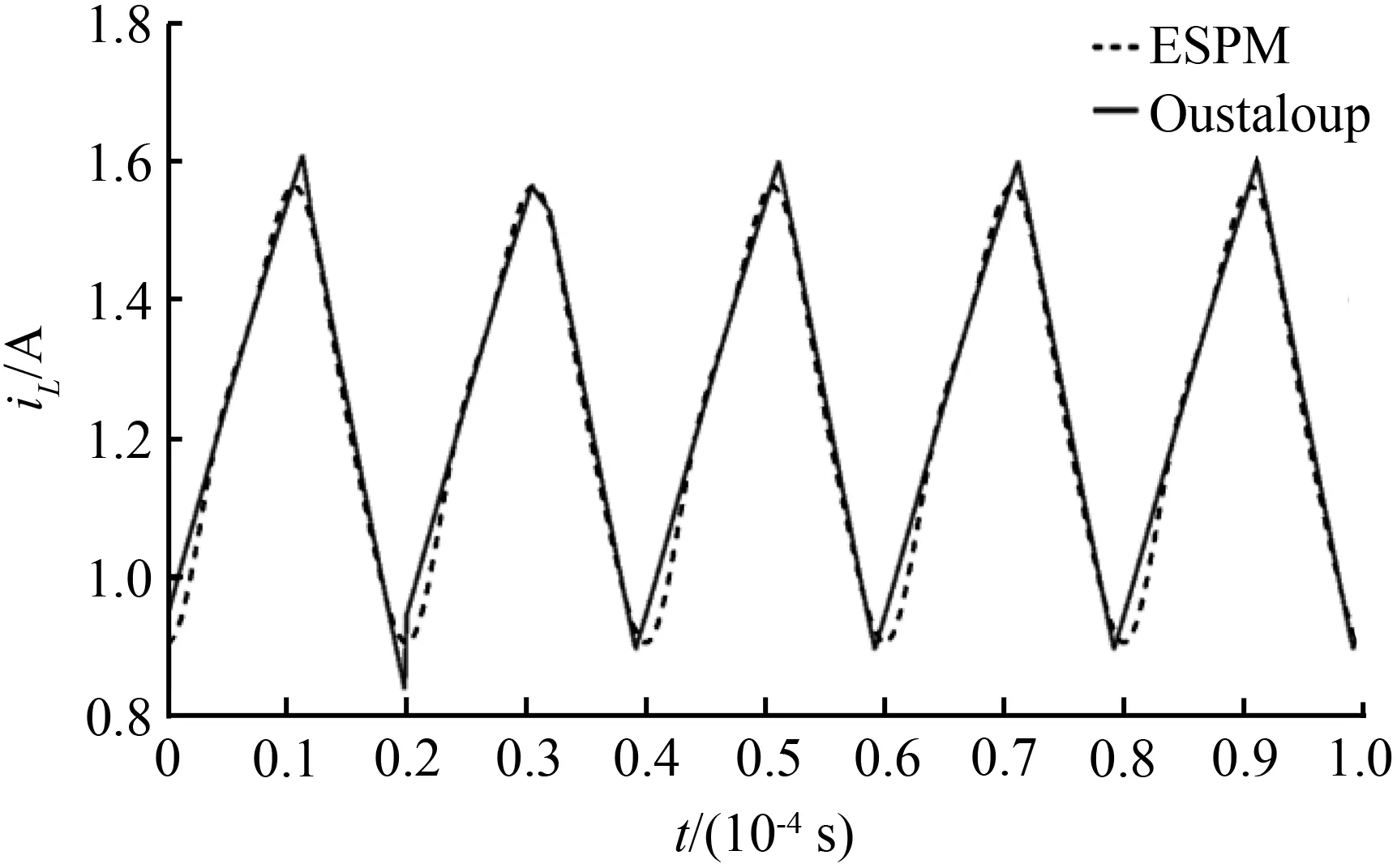
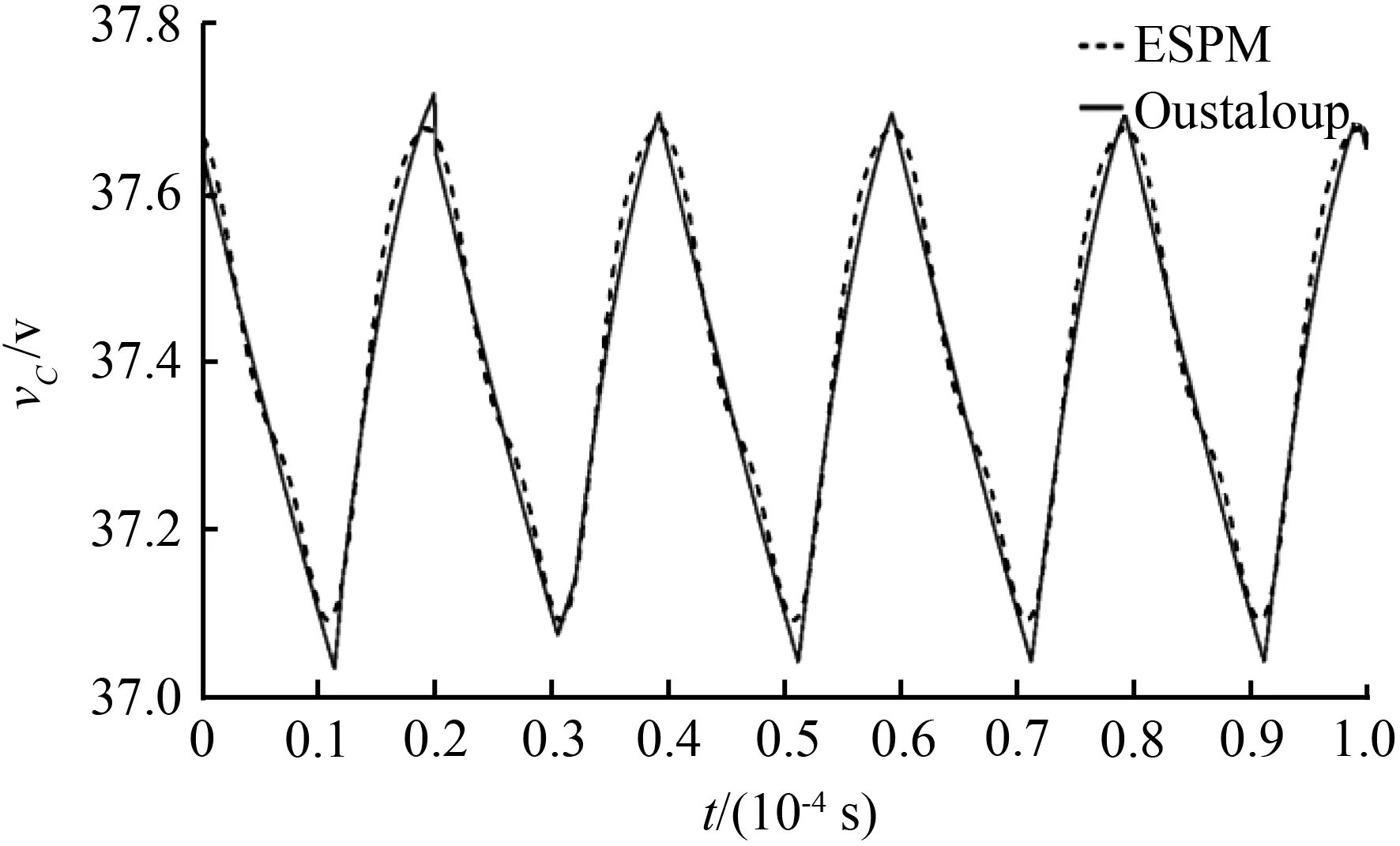
工作模态1(0 (3) 工作模态2(DTs (4) 式中,D为占空比。 在本文中,采用算子符号pα和pβ分别代dα/dtα和dβ/dtβ,则有 G0(pα,pβ)x+G1f(x)-G2t(x)=0, (5) 式中,非线性函数f(x)=δ(t)x;非线性函数t(x)=δ(t)e,e=[Vin/L,0]为一个与输入电压有关的常向量;状态向量x=[iL,vC];G0、G1、G2是系数矩阵,其表达式分别如下: (6) 式(6)是分数阶Buck-Boost变换器在CCM的状态向量模型。通过式(6)可以看出,系数矩阵G0(pα,pβ)与变换器的电感和电容分数阶阶数有紧密的联系。 ESPM可用于求解整数阶变换器或受迫振荡非线性系统的稳态解析[12]。因此,本文采ESPM来对分数阶变换器进行稳态求解与分析。 对谐波平衡原理的推广有如下表达式[13]: (7) 式中,γ是微分运算的阶次,可以为整数,也可以是分数;ω是指数函数的角频率。 根据ESPM的定义,将分数阶变换器的状态向量展开如下所示: (8) 式中,x0是状态向量的主振荡分量的值,xi是第i阶修正量的值。 同理,开关函数δ(t)也可以展示成同样的级数之和: (9) 式(8)和式(9)中的λi是表示标记修正量xi和开关函数δi的系数。 将状态变量x和开关函数δ(t)的展开式代入f(x)=δ(t)x,将δ(t)和e代入非线性函数t(x)=δ(t)e。 (10) 式中: (11) 根据谐波平衡原理,假设xi的表达式为 (12) 式中,c.c代表共轭项,k表示谐波的次数,τ=ωt,ω是指数函数的角频率。ai0代表第i阶修正量的直流成分,aik代表第i阶修正量第k次谐波幅值,谐波成分{Eir}是由建模对象的实际物理特性决定的。 对于DC-DC变换器,状态变量主要由直流量构成。假设振荡分量x0的谐波成分集{E0}={0}.其他阶修正量xi的谐波成分集合{Eir}由余部Ri确定。当变换器处于CCM时,δ(t)可展开成傅立叶级数,如下所示: (13) 式中,b0=D,bk=(αk-jβk)/2,且有 (14) δ0和δi的表达式分别为 (15) 将xi和δi代入f(x)=δ(t)x中,由于xi和δi的相乘关系,导致fi中有新的谐波成分产生。将δi和e代入t(x)=δ(t)e中,由于e是一个常数矩阵,所以ti的谐波成分只由δi确定。则有 (16) 式中,fim表示fi中与xi相同的分量,Ri+1表示fi中其他的分量,tim为ti中与xi相同的分量,Hi+1为ti中其他的分量,xi的频谱和Ri与Hi相同所以在运算中可以由Ri与Hi确定xi频谱的值。 将xi和fi与ti的表达式代入式(5)中,可以得到 (17) 由式(17)可以逐步得到主振荡分量和各阶修正量,如果满足以下条件: (18) 则停止迭代。 假设状态向量只有直流成分,则有 (19) 同理,可得 (20) 将x0、tom和fom代入式(17)的第一项表达式中可得 G00a00+G1Da00-G2De=0, (21) 式中,系数矩阵G00=G0(0,0)。 根据谐波平衡原理,可以得到 (22) 由式(22)可得a00的解析式,再由f0的余部R1,可得修正量x1的谐波成分集为{E1r}={1},可以假设 x1=a11ejτ+c.c, (23) 式中,a11=[I11,V11]。 将x0、x1、δ0、δ1代入式(11)的第一个式子,可以得到f1m和R2的表达式分别为 (24) 式中,f1m含有和x1相同的谐波成分,f1剩余的谐波放在R2中。 由于H1的频谱{K1r}={1},则x1的频谱也为{1},则可以得到 t1=δ1e=b2e·ej2τ+b3e·ej3τ+c.c, (25) 同理,选取t1中与x1频谱相同的量t1m,其余分量为H2,则有 (26) 将x1、R1、f1m、t1m和H1代入式(17)第二个式子中,则有 (G01+G1b0)a11=-G1b1a00+G2b1e, (27) a11可以通过以下线性方程获得: (28) 对于二阶修正量x2,由式(24)可得H2的频谱为{K2r}={2,3},根据f2的余部R2可得二阶修正量的成分{E2r}={0,2,3},由此可以确定二阶修正量x2的表达式为 x2=a20+a22ej2τ+a23ej3τ+c.c, (29) 二阶修正量中的直流成分为a20=[I20,V20]T,二次谐波为a22=[I22,V22]T,二次谐波为a23=[I23,V23]T。可以得到f2中与二阶修正量x2相同的谐波成分 (30) 由于: t2=δ2e=b4e·ej4τ+b5e·ej5τ+c.c, (31) 选取t2中与x2相同分量的t2m,其余部分为H3,可以得到 (32) 将x2、R2、f2m以及H2和t2m代入式(17)的第三个公式: (33) (34) (35) (36) 这样就可以求出aik的各个表达式,得到各阶修正量的表达式,则状态向量的解析表达式为 x=x1+x2+x3=a00+a20+(a11ejτ+a22ej2τ+a23ej3τ)+c.c。 (37) 电感电流iL和电容电压vC的表达式分别为 (38) 式中,Re和Im分别表示实部与虚部。 aik的表达式见表1。 表1 aik 中电感电流和电容电压解析表达式 表1中,(△jkω)表达式为 Δ(jkω)=(1-D)2+(jkω)α+βLC+(jkω)αL/R。 (39) 仿真参数如下:电源电压Vin=25V,负载电阻R=80 Ω,开关管占空比D=0.6,开关变换器的频率fs=50 KHz,分数阶电感L=5 mH,分数阶电容C=0.1 mF/s1-β。 用等效小参量法和Oustaloup频域滤波法[14]得到的状态变量的直流成分比较见表2,表2中的(a00+a20)分别表示电容和电感电流的直流成分。 表2 状态变量直流成分比较 从表2可知,等效小参量法和Oustaloup频域滤波法得到的电感电流、电容电压直流分量结果相差很小,且两者的变化趋势一样。 采用Oustaloup频域滤波法和等效小参量法所得的不同阶次电感电流和电容电压波形图分别如图2和图3所示,图中的蓝色虚线和红色实线分别是是用等效小参量法和Oustaloup频域滤波法得到曲线。 (a)(α,β)=(0.8,0.8) (a)(α,β)=(0.8,0.8) 从图2和图3可以看出,电感电流以及电容电压和表2变化的趋势一致。仿真结果表明,变换器的电流纹波以及电压纹波都与电感和电容的阶次有密切的关系,随着储能元件阶次α和β的增大,变换器的电感电流和电容电压纹波值相应的在减少。 变换器处于CCM的前提是变换器的电感电流平均值大于其纹波[15]。分数阶Buck-Boost变换器满足以下判别式时,变换器运行于CCM: (40) 式(40)中,Г(α)是伽马函数。 由文献[16]给出分数阶Buck-Boost变换器电感电流纹波表达式为 (41) 由式(38)可知直流量I00+I20是变换器的直流量,也就是电感电流的平均值。在满足修正终止判别的条件下,可得到一种新的判断变换器工作模态的方法,判别式如下所示: (42) 当N>0,变换器运行于CCM;当N<0,变换器运行于DCM。当N=0,变换器运行于CCM和电感电流断续临界模式下。 根据式(41)得到CCM的分数阶Buck-Boost变换器稳定工作时,其电感和电容阶数的区域如图4所示。图中,绿色区域部分是根据文献[16]给出的变换器处于CCM的判别式所得,基于ESPM的判别式所得的是绿色和红色区域。 图4 分数阶CCM Buck-Boost变换器稳定工作时的电感和电容阶数的区域 由图4可知,变换器稳定工作主要取决于电感的阶数,电容的阶次对工作模态也有一定的影响,文献[16]的判定条件忽略了电容阶次对工作模态的影响。 为验证变换器工作模态判别条件,在Simulink对电容阶次为0.5阶,电感阶次不同时的CCM的分数阶Buck-Boost变换器进行仿真,电感电流波形如5图所示: 由图5可知,当α=0.8时,变换器仍然运行于CCM,而根据文献[16]所提出的电感电流判定条件,在α=0.8时已经处于DCM。因此,本文提出的分数阶Buck-Boost变换器CCM的判断方法比Caputo定义下的判断方法更准确。 图5 不同电感阶次下的电感电流波形 在不同阶次时对电感电流和电容电压的谐波值进行比较和统计,得到电感电流和电容电压的一阶、二阶和三阶的谐波成分表,分别如图6、图7所示。 图6 不同阶次的电感电流中谐波成分 图7 不同阶次的电容电压中谐波成分 由图6和图7图可知,随着电感和电容的分数阶阶次的降低,电感电流和电容电压的一次、二次和三次谐波的值在增加。 通过各个谐波幅值的变化对式(18)所提出的解析解修正终止判别条件进行验证,对判别稳定性的条件与谐波成分情况进行分析,可得变换器电感电流和电容电压中谐波成分有效值占基波分量百分比,如图8所示。 由图8可以看到,随着电感和电容的分数阶阶次的降低,修正终止判别条件的值也在增加。当电感和电容的阶次都为0.8时,正好达到临界值1 %。 图8 变换器状态变量中谐波成分有效值随阶次变化情况曲线 文章基于扩展的谐波平衡原理,结合扰动的思想,应用ESPM,避开了几种分数阶微积分定义适用性的讨论,对分数阶Buck-Boost变换器进行了稳态特性的研究。根据稳态解析表达式,在Matlab中对分数阶Buck-Boost变换器进行建模,并与Oustaloup频域滤波法进行对比。研究结果表明: ① ESPM克服了分数阶系统难以获得显示表达式的问题,所得的解具有实际物理意义,解决了几种分数阶微积分定义在DC-DC变换器中难以适用的问题,与频域近似法所得的结果一致。 ② 变换器电感电流和电容电压的直流成分和纹波均与储能元件的阶次有关,在其他参数不变的情况下,当电感和电容分数阶阶次减小,状态变量中各个阶次的谐波成分的幅值会增大,造成分数阶变换器电感电流和电容电压纹波幅值的增大。 ③ 电感电流运行于连续模式主要取决于电感阶次α,但也和电容的阶次β也有一定的关系。本文提出的新的判定CCM的方法,比Caputo定义下的判定方法更准确。通过仿真验证了理论分析的正确性。2 基于ESPM的分数阶Buck-Boost变换器等效模型
2.1 基于扩展谐波平衡原理的ESPM原理
2.2 分数阶Buck-Boost变换器稳态解析解

3 仿真分析
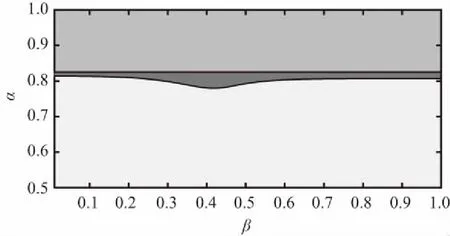
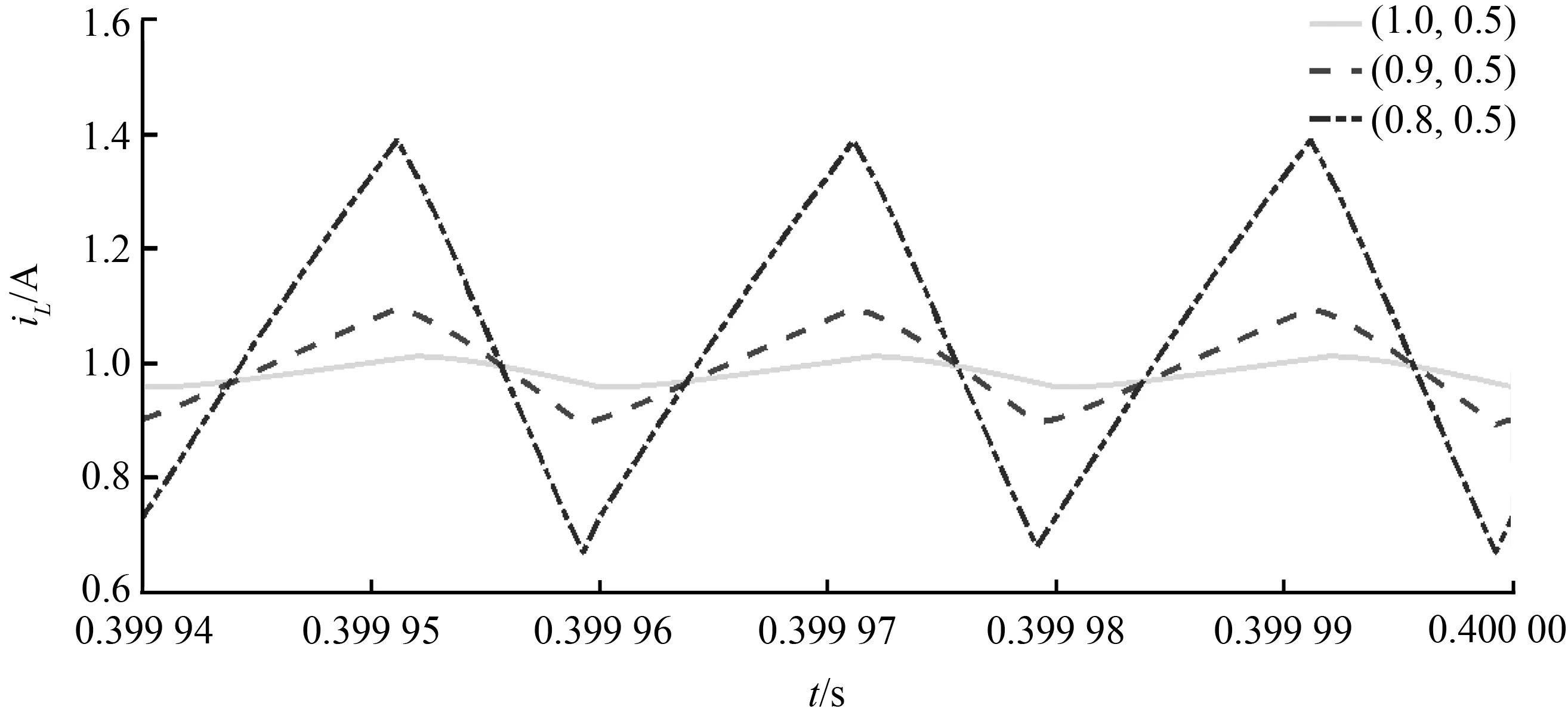
4 分数阶Buck-Boost变换器CCM判别条件
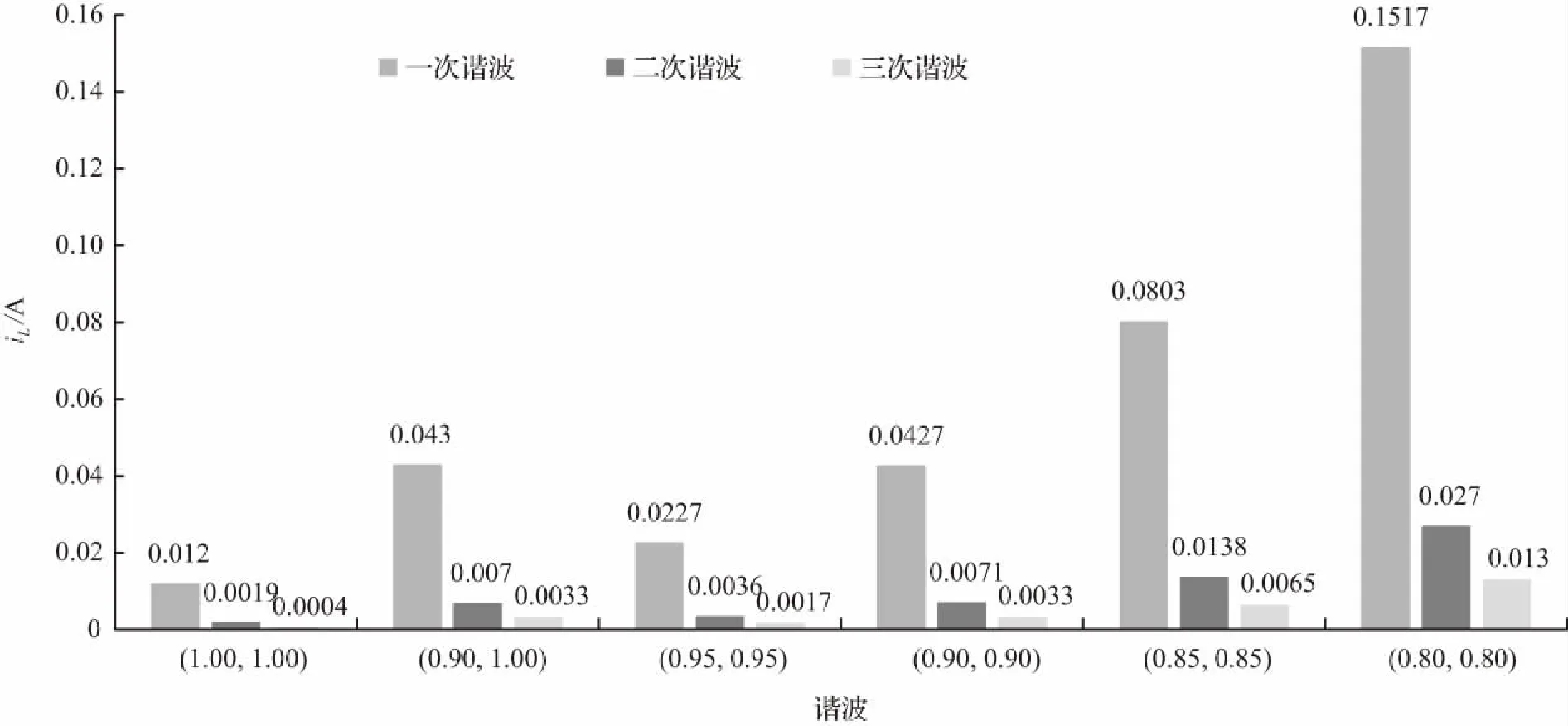
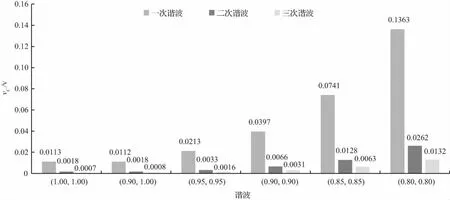
5 ESPM对谐波成分特性分析

6 结论

