基于GEMS算法的潜变量高斯图模型结构学习

郑倩贞，徐平峰，曹 蕾

(长春工业大学数学与统计学院，吉林 长春 130012)

高斯图模型能够清晰直观地反应变量间的相互关系，被广泛应用于高维情形.在对实际问题进行图模型结构学习时，仅考虑观测变量有时并不能正确反应变量间的相互关系，因此需考虑潜变量对可观测变量的影响，在给定潜变量时探讨可观测变量间的条件关系.Chandrasekaran等[1]将可观测变量的边缘协方差阵的逆阵分解为一个稀疏阵和一个低秩阵，提出了惩罚似然的方法，对稀疏阵和低秩阵分别施加1范数及核范数惩罚，并结合凸优化和代数几何对潜变量图模型选择问题进行了研究.Yuan[2]基于Chandrasekaran等人的研究，将惩罚似然的核范数惩罚项替换为对低秩阵的秩的约束条件，提出了潜变量GLasso(LVglasso)方法，并结合EM算法对高维情形下的潜变量图模型选择问题进行了模拟研究.Lauritzen等[3]对惩罚似然做了与Yuan相似的处理，采用插补的方法，结合EM算法和GLasso算法进行模型选择.

但上述与EM相结合的方法需要先给定1组正则化参数，然后对每个正则化参数利用EM算法求惩罚似然的最小值点.如果正则化参数选取不当，将会导致每次迭代的模型离真模型越来越远，而且增加计算时间.本文基于期望模型选择(EMS)算法[4]的思想，在每次迭代时从候选模型中选取期望信息准则最小的模型作为下一步的当前模型，下一次迭代时在当前模型下求候选模型的期望信息准则的值.但由于可能的模型太多，在模型选择时遍历全部模型不可行，因此只选出部分模型作为候选模型.这里的候选模型也可以通过1组正则化参数来确定，但每次的正则化参数不一定相同.称这种方法为广义期望模型选择(GEMS)算法.模拟实验显示，基于GEMS的LVglasso方法收敛速度快，计算时间短.

1 高斯图模型

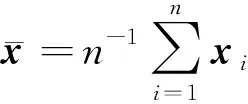
Yuan等[5]提出通过最小化负1惩罚对数似然的方法去估计高斯图模型的协方差逆阵Ω，惩罚似然为

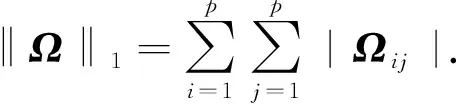
2 LVglasso方法

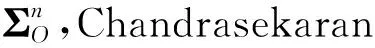
其中：S-L≻0表示S-L为正定矩阵；L0表示L为非负定矩阵；为ΩO的估计，为的估计；为可观测样本的对数似然函数，即

基于Chandrasekaran等[1]提出的惩罚似然，Yuan[2]提出了计算更加方便的LVglasso方法：

其中：0≤r≤p，S†=S-diag(S).限制条件rank(L)≤r相当于假设存在r个潜变量.

考虑完全数据x=(x1，…，xn)T=(xO，xH)，xi=(xO，i，xH，i)T，其中xO，i为第i个样本的可观测数据，xH，i为第i个样本的不可观测数据，i=1，…，n.Ω的LVglasso估计为

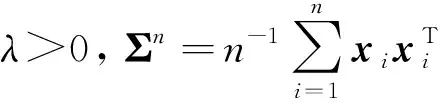
3 GEMS算法

EMS算法[4]是一种迭代算法，用于处理缺失数据情形下的模型选择问题.该算法的每次迭代都需给定当前模型Mc和当前模型下的参数θc∈ΘMc，并依次进行期望步(E步)和模型选择步(MS步)，直至满足停止准则得到最优的模型估计M*和参数估计θ*∈ΘM*.本文的GEMS算法与EMS算法类似，不同之处在于：GEMS算法的MS步不遍历全部模型，而是通过GLasso算法找出候选模型，候选模型可由1组正则化参数来确定，且每次迭代的正则化参数可能不同.在这些候选模型中选择期望BIC最小的模型，然后将该模型及其对应的参数作为下一次迭代的当前模型和当前参数.从部分而非全部模型中选择最优模型可大大减小计算成本，提高计算效率，尤其是在高维问题中.考虑潜变量高斯图模型的结构学习问题，现有当前模型G(t)及当前参数Ω(t)，则第(t+1)次迭代如下：

(1) E步

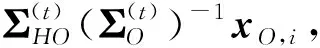
进而，有Q函数

Q(G，Ω|G(t)，Ω(t))=Et(-2(G，Ω))+log(n)dfG= -nlogdetΩ+ntr[ΩEt(Σn)]+log(n)dfG.

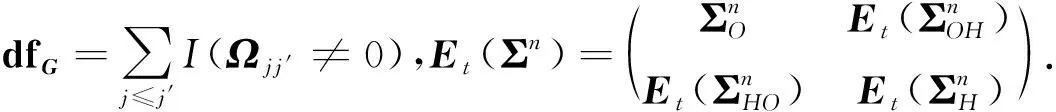
(2) MS步

因此，可得到1组候选模型G={G(t)，Gλm，m=1，…，k}.针对每个候选模型G∈G，计算Q函数，从而得到Ω的估计Ω(t+1)=argminΩQ(G，Ω|G(t)，Ω(t))及其对应的图模型G(t+1)=argminG∈GQ(G，Ω(t+1)|G(t)，Ω(t)).

将G(t+1)，Ω(t+1)作为下一次迭代的当前模型和当前参数，重复以上步骤直至满足停止准则.

4 模拟实验及实例分析

在模拟实验中，考虑不同情形下潜变量图模型的结构学习问题，对GEMS算法和EM算法在LVglasso估计求解问题上的模拟结果进行了比较.模拟实验覆盖p=48，98，148，198，h=2，r=2，5，n=500，1 000共16种情形，每种情形各模拟50次.真模型产生机制与Yuan[2]类似，两者的不同之处体现在对潜变量的设定上.在本文真模型中，每个潜变量至少和2个可观测变量、至多和(p-1)个可观测变量有关.值得注意的是，当在进行n=1 000，p=198，r=2情形设定下的第38次EM算法模拟时，由R中lvglasso函数产生的Ω迭代初值为非对称阵，所以该种情形只模拟了37次.16种情形的CPU平均运行时间如表1所示.

表1 不同情形下CPU平均运行时间 s

从表1中可看出，对于任意一种情况，EM算法的运行时长都要远大于GEMS算法，达到5倍、10倍，甚至是15倍的差距.GEMS算法大大提升了潜变量图模型选择的速度.本文用于评价算法性能的指标为：

其中tp，tn，fp，fn分别为真阳类、真阴类、假阳类、假阴类的个数.图1给出了所有情形下tpr，ppv和mcc的箱线图.总体上看，GEMS较EM有更优的表现，但在极个别情况如n=500，p=198，r=2或5时EM的tpr值较大.同时可看出，样本量越大，潜变量个数的假设越接近真实模型，模型推断就越准确.

白色箱子代表EM算法，灰色箱子代表GEMS算法，横轴为真模型可观测变量的个数.

基于GEMS算法，对Wille等[7]论文中拟南芥植物类异戊二烯生物合成相关基因的数据进行了潜变量高斯图模型结构学习，估计了各基因间的条件相关性.该数据的数据来源为https：∥static-content.springer.com/esm/art%3A10.1186%2Fgb-2004-5-11-r92/MediaObjects/13059_2004_896_MOESM1_ESM.txt，数据中共有118个样本，每个样本包含39个基因表达.若假设的潜变量个数不同，则推断出的各基因间的条件相关性也不同.假设潜变量个数为r=1或r=3时的估计结果如图2所示.当r=1时，共估计出174条边，算法运行时间约为43 s；当r=3时，共估计出38条边，算法运行时间约为10 s.

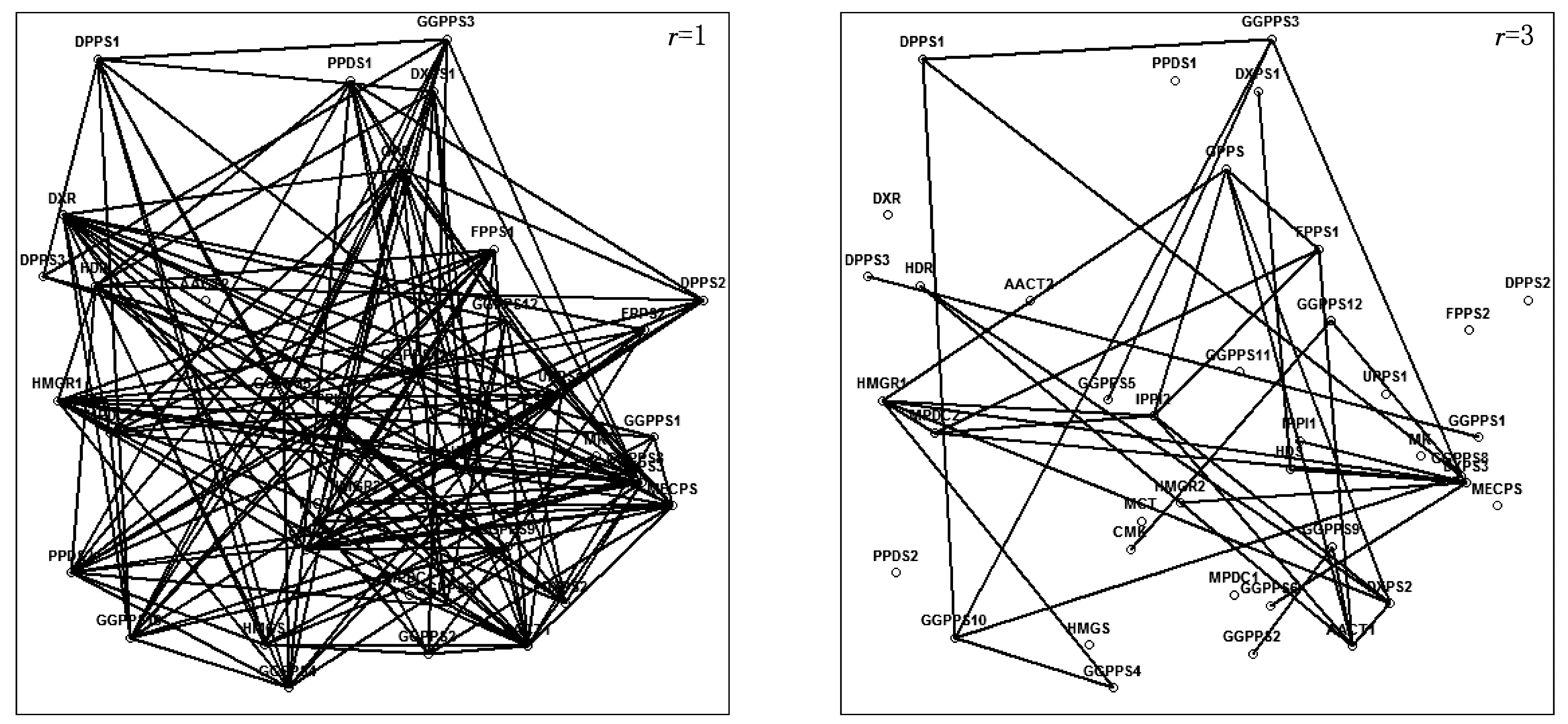
图2 r=1和r=3时的基因图模型

5 结语

本文简要介绍了高斯图模型及潜变量高斯图模型下的LVglasso方法，给出了GEMS算法结合LVglasso下潜变量图模型结构学习的算法步骤，并从模拟实验的角度比较了GEMS算法和EM算法在潜变量图模型选择问题上的优劣.通过多种不同情形下的模拟实验，可以发现，样本量越大，潜变量个数的假设越接近真实模型，模型推断就越准确.结合tpr，ppv，mcc以及CPU平均运行时间，无论在何种模拟情形，GEMS算法在模型选择上的表现较EM算法优越.