海水中声波信号检测算法研究
胡雨露,王连明
(海南热带海洋学院海洋科学技术学院,海南 三亚 572022)
0 引言

图1 海水中声波通信过程
声波是海水中进行信息传输的主要手段,海面上的设备可以通过声波与水下设备进行通信,如图1所示.但是在海洋环境中,海面风浪、海洋生物活动、海上航运等自然和人为活动产生的声波,在传播过程中会与海面、海底、水体等发生相互作用,形成一个复杂的背景噪声场,这些噪声就是通常所说的海洋环境噪声[1].海洋环境噪声会对正常的声波通讯信号造成干扰,使信噪比下降.另一方面,由于采用声波通信的信源和信宿通常存在相对运动,会产生多普勒效应,使接收到的声波频率发生偏移,这些问题会导致检测有用声波信号的难度增大.同时,由于海底供电困难,通常要求声波检测设备具有功耗低、运算速度快等性能.因此,研究简单高效适用于低功耗硬件实现的、抗干扰、抗频移能力强的声波信号检测算法具有实际意义和研究价值.
目前,国内外学者在研究信号检测问题上,针对不同问题,给出的解决方案也不尽相同.文献[2]对微弱信号检测的方法进行了理论上的分析;文献[3-5]提出了在海洋环境背景下,使用随机共振检测水声信号的方法,但这一方法需要构造复杂的非线性系统,计算量增大,复杂度高,且不适于硬件实现;文献[6]提出使用核磁共振的方法进行信号检测,虽然在理论上检测效果较好,但计算复杂,硬件实现成本高;还有一些改进的算法,如混沌理论方法、神经网络等也都局限于理论仿真.
针对上述问题,本文在建立海水中声波信号传输模型基础上,通过比较相关分析、频谱分析、功率谱密度分析以及短时傅里叶变换等信号检测方法,提出了在低信噪比、存在频移情况下,适于低功耗微处理器进行实时声波检测的可行方案.
1 多普勒效应
多普勒效应是由于接收端与发射端的相对运动产生的,如果接收端与发射端之间发生的是相向运动,那么波长会变短,频率会增大;相反,如果接收端和发射端之间发生的是相对运动,那么波长会变长,频率会减少.在海水中,产生多普勒效应的原因主要分为两个:一是由于海水的运动,会产生多普勒拓展,即声波信号的频率会发生拓宽.随着海面波浪的增加,水面的粗糙度也会变大[7],但对频率的影响相对比较小,通常可以忽略不计;二是由于声波发射端相对海下的声波检测系统会产生相对运动,则接收端接收到的声波信号会发生多普勒频移现象[8].多普勒频移现象遵循公式
(1)
其中:v为接收端与发射端的相对速度;c为海洋中声音传播的速度;f是发射端发射的声波信号频率;cosθ为声波传播方向与发射端和接收端相对运动方向的夹角余弦,为了方便计算,通常取cosθ=1,可以得出最大多普勒频移.声音在海洋中的传播速度与海水的温度、盐度和深度有关,我国在1998年出台的《国家海道测量规范》中给出的海洋声速经验公式为[9]
c=1 449.2+4.6t-0.055t2+(1.34-0.01t)(s-35)+0.017.
(2)
其中:c为声速,t为海水的温度,s为盐度.根据海水不同的温度、盐度以及水深可以得出不同的声速,进而得到不同的多普勒频移.
假定海洋中海水的温度t为15℃,盐度s为3.5%,轮船正常行驶的运动速度为8 m/s,即发射端与接收端的相对运动速度v为8 m/s,根据海深和声波信号频率的不同可以得出多普勒最大频移,如表1所示.根据指定的声波信号频率和水深,可以得出多普勒频移量.
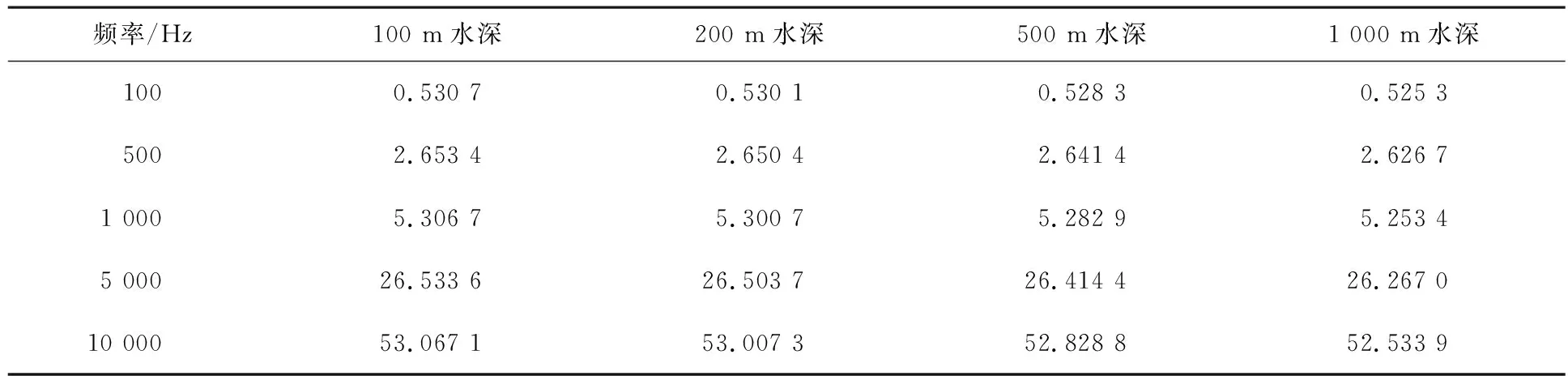
表1 海水中多普勒频移
2 海水中的声波传输模型
海洋中噪声的成分多种多样,根据来源的不同,可大致分为3类:第1类是海洋中的生物噪声,如鱼类、头足类等,它们的生命活动会产生噪声;第2类是海洋中的动力噪声,例如海水运动形成的海浪等;第3类是海洋中的人为噪声,例如海上航运、潜艇等产生的噪声.不同噪声源发出的噪声叠加在一起,会形成复杂的混合噪声,但是每个噪声源又是相互独立的,彼此之间不相互干扰.如果噪声的概率密度分布满足公式
(3)
则称此噪声为高斯噪声,其中μ为均值,σ为方差.由于海洋环境噪声具有很强的随机性,其统计特性分析一直是海洋环境研究的重点[10],海水中总噪声的幅值呈高斯分布,因此通常将海水中的混合噪声简化为高斯白噪声.
在已知噪声统计特性的基础上,本文构造了声波检测所需要的信号模型.假设发射端发射一个双频叠加的特征信号x(t)=Asin(2πf1t)+Bsin(2πf2t),经过海洋中各种噪声产生干扰以及多普勒频移后,接收端接收到一个混合信号y(t)=Csin(2π(f1±fd1)t)+Dsin(2π(f2±fd2)t)+n(t),其中fd1和fd2均为多普勒频移量,n(t)为高斯白噪声.
3 信号检测算法介绍
3.1 相关检测法
相关检测的原理是比较两种信号的相似程度,在信号检测中,通常采用互相关方法,通过计算特征信号x(t)和混合信号y(t)的相关程度,判断混合信号是否含有特征信号,公式为
Rxy=E[x(t)y(t+τ)].
(4)
其中τ为时间延迟.设定某个阈值,当接收到的混合信号仅为纯噪声时,特征信号和噪声的相关系数小于设定阈值,可以认为几乎不相关;当混合信号中含有与特征信号相同或相近(多普勒频移范围内)的频率成分时,特征信号与混合信号的相关性将会大于该阈值,系统可以判断接收端存在该频率成分的信号.
3.2 频谱分析法
在信号检测中,一般利用傅里叶变换来对信号的频谱进行分析,傅里叶变换的公式为
(5)
通过将接收端得到的混合信号y(t)进行傅里叶变换,判断是否存在与特征信号同频率的成分,并根据该频率成分的幅值判别信号是否到来.
3.3 功率谱密度分析
功率谱密度反映了信号的功率随频率的分布情况,当信号为广义的平稳过程时,其功率谱密度才存在.根据维纳-辛钦定则,如果信号是平稳信号,其功率谱密度与自相关函数是一对傅里叶变换对.因此,假设混合信号y(t)为平稳信号,其功率谱密度为
(6)
其中:R(m)为混合信号的自相关,Sx(ω)即为所求信号的功率谱密度,单位为W/Hz.由于噪声的功率比较低,特征信号的功率能够清晰显示出来.利用功率谱密度对混合信号进行分析,能够弥补傅里叶变换受幅值影响的缺点,有效抑制噪声的干扰,才能将多普勒频移后的特征信号的频率筛选出来.
3.4 短时傅里叶分析
由于傅里叶变换是将整个时域上的波形进行频域展开,缺少时域定位功能,因此短时傅里叶变换在傅里叶变换的基础上给信号加上了一个窗函数,通过移动窗函数,可以得出不同时刻的功率谱.短时傅里叶变换可以通过加窗的方式将非平稳的信号转换为平稳信号.短时傅里叶变换是和傅里叶变换相关的一种数学变换,其变换遵循公式为
(7)
其中w(n-m)为窗函数.短时傅里叶变换使用的是一个固定的窗函数,即得到一个固定的分辨率.如果需要改变分辨率,则需要改变窗函数.信号经过短时傅里叶变换后,可以清楚得到频率所产生的时刻和对应的功率.
4 几种算法性能的仿真比较
为测试各种算法的有效性,在MATLAB2015环境中,分别从信噪比、多普勒频移以及计算量3个方面对各种算法的性能进行仿真比较.
4.1 信噪比对检测性能的影响
在多普勒频移不变的情况下,通过改变信噪比进行分析.其中,图2(A)为相关检测法,横坐标为不断增大的信噪比,纵坐标为不同信噪比下的最大相关系数;图2(B)为傅里叶变换、功率谱密度以及短时傅里叶变换,横坐标为不断增大的信噪比,纵坐标为噪声最大傅里叶变换系数与信号最大傅里叶变换系数的比值,该比值越小,说明信号越强.
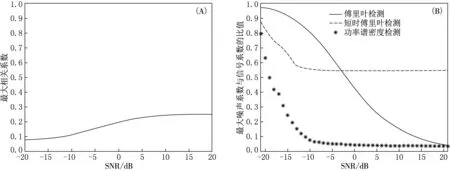
(A)SNR对最大相关系数的影响;(B)SNR对检测算法的影响
从图2(A)中可以看出,相关检测法在信噪比大于-14 dB的情况下,可以通过设定阈值和最大相关系数比较,判断混合信号中是否含有特征信号,但是在整个信噪比变化范围内,效果不明显.如图2(B)所示,傅里叶变换、功率谱密度分析以及短时傅里叶变换都是通过最大噪声系数与信号系数的比值大小来判断特征信号是否存在.傅里叶变换在信噪比大于-15 dB后,比值趋于稳定;功率谱密度在信噪比大于-8 dB后,可以抑制噪声干扰,最大噪声系数与最大信号系数的比值趋于稳定且取值较小,即信号在噪声中更容易检测;时频域分析的短时傅里叶变换在整个信噪比变化范围内波动性比较大,即受信噪比影响比较大.
4.2 多普勒频移对检测算法的影响
在信噪比不变的情况下,根据(1)和(2)式,通过改变海水深度来控制多普勒频移量的变化,对几种算法进行仿真比较.其中,相关检测法的横坐标为不断增加的海水深度,在满足海洋声速经验公式的条件下,从100 m逐渐增加到1 000 m,纵坐标为不同海深下对应的最大相关系数;傅里叶变换、功率谱密度以及短时傅里叶变换的横坐标也为不断增加的海水深度,纵坐标为噪声最大傅里叶变换系数与信号最大傅里叶变换系数的比值,比值越小,说明信号越强(见图3).
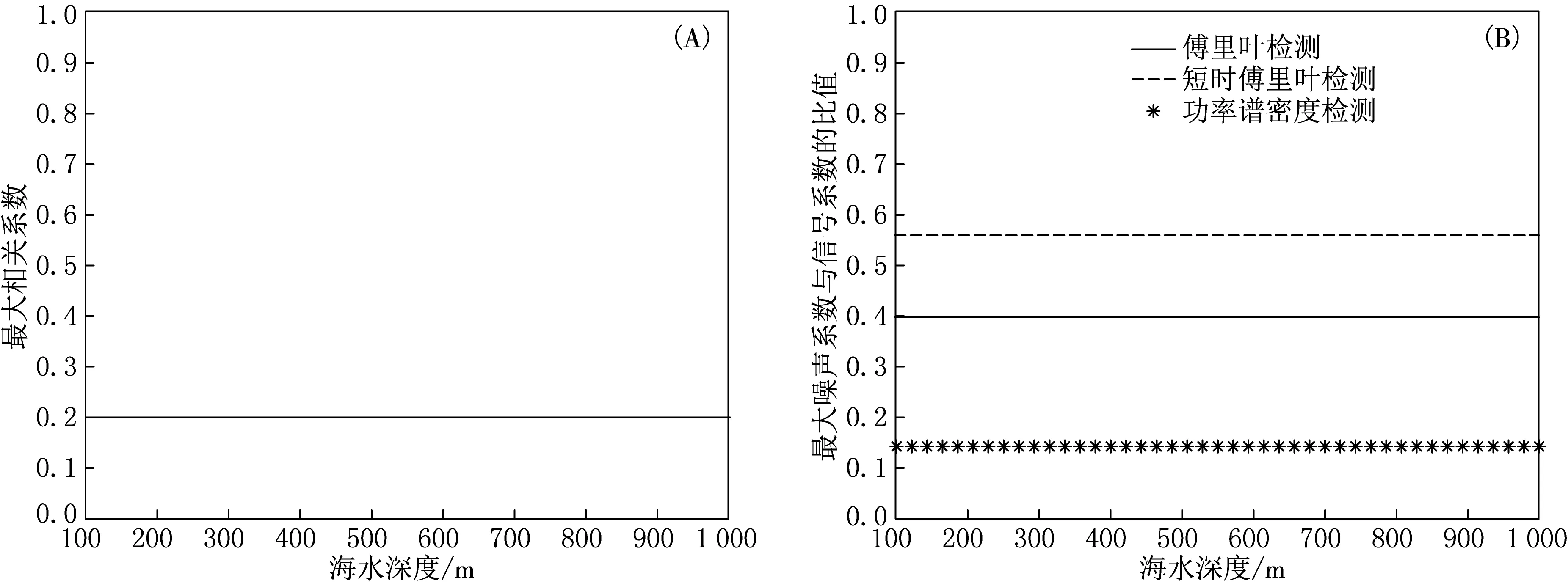
(A)频移对最大相关系数的影响;(B)频移对检测算法的影响
从图3中可以看出:随着海水深度的不断增加,这4种检测方法的噪声最大傅里叶变换系数与信号最大傅里叶变换系数的比值在[0,1]范围内几乎不变,即4种检测方法均不受多普勒频移的影响.其中功率谱密度的噪声最大系数与信号最大系数的比值最小,特征信号最明显.
4.3 几种算法计算量的比较


表2 几种算法的计算量比较
5 结论
经过上述几种算法的分析比较,可以看出快速傅里叶变换检测法能够较好地抑制噪声的干扰,几乎不受多普勒频移的影响,同时计算量小,能够满足硬件设备功耗低、速度快的要求.
另一方面,在海洋背景下,如果接收端和发射端产生相对运动,多普勒效应所产生的频移影响在原来频率的0.5%左右,因此在检测特征信号时,可以通过前置一个带通滤波器,将混合信号中的无关频率和噪声滤掉,然后再使用快速傅里叶变换的方法实时进行有用声波信号的检测.

