过采样和非线性校正在中子发生器控制台上的应用

郭纪佑，范 琦，乔 双

(东北师范大学物理学院，吉林 长春 130024)

中子管是将离子源、加速系统、靶以及气压调节系统密封在一个陶瓷或玻璃管内，形成电真空器件.中子管与之匹配的储存器电源、离子源电源、加速高压电源及相应的控制与检测电路共同构成小型中子发生器.小型中子发生器是目前中子源最热门的技术之一，它具有易携带、单色性好、中子能量高、使用安全、维护方便等优点[1].但在实际应用中，发现许多SOC上(如STM32F407)集成的A/D转换器，其采集精度不能满足测量要求.主要是由于AD采集分辨率不足以及AD采集电路线性度不高造成.针对上述问题，为了优化算法保证系统稳定性、提高数据采集精度而采用了过采样算法技术，将12位的AD采集分辨率扩展到16位，并将采集结果利用最小二乘法拟合，减小非线性误差，保证AD采集的精度.提高了中子发生器的稳定性，进而稳定中子产额.

1 中子发生器

1.1 中子管的结构及原理

中子管结构如图1所示.其工作原理：离子源内电子在电场和磁场的共同作用下产生螺旋往复运动，与氘氚气体分子发生碰撞产生氘氚离子，这些离子的一部分由加速电极的高压所形成的电场引出并加速，在中子管的靶上高速碰撞后发生核反应产生中子[2].

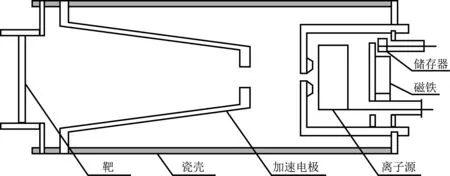
图1 中子管结构

1.2 中子发生器控制台

中子发生器以STM32F407芯片为核心组成主控电路，通过串口电路与上位机通信，由AD输出调控储存器、离子源、高压源三路电源，并通过AD数据采集电路实现对各路电源及中子管状态的实时采集，各电路模块之间加入数字隔离电路[3]，控制台整体框图如图2所示.

图2 控制台硬件系统整体框图

中子管电参数通过缓冲电路送入单片机进行AD转换，但在实际测试发现由于缓冲电路中运放、电阻、电容及片上AD转换器等器件的精确度不够高[4]，导致采样电路非线性的产生.因此本文提出采用最小二乘法对其进行非线性校正，同时考虑到芯片内部AD精度不高而外部AD采集芯片昂贵的情况，采用过采样技术来提高其分辨率，减小了硬件空间.

2 过采样技术

2.1 过采样理论

2.1.1 量化噪声分析

AD采样过程其实是一个将连续的模拟信号量化成有限的数字过程，每个数字代表一次采样所获得的信号.量化时，根据数据位把整个幅度划分为量化级，由于模拟信号是连续的，量化结果和被测模拟量之间会存在差值，该差值被称作量化误差(eq)，也称量化噪声.

能够确定最小的分辨率为

(1)

其中Vref为参考电压，N为量化的数字位数.

由公式(1)可知，N越大，Δ就越小，量化误差也就越小.在没有其他能造成误差的因素(例如热噪声、杂散噪声、参考电压变化)的理想情况，量化误差应该在±0.5Δ之内，即|eq|≤0.5Δ.假设输入信号的变化大于Δ，并且在Δ间是随机分布(即量化误差随机，P(eq=1)的时候)，可以将量化噪声看成白噪声，其总功率为一个常数.由于噪声总功率一定，所以fs越大，叠加在信号部分的量化噪声就越小[5].

2.1.2 过采样率和精度之间的关系

根据前面的假设，量化噪声为白噪声，则可以通过计算量化误差的方差来得到平均噪声功率，公式为

(2)

其中eq为量化误差，Δ为最小分辨率.

由此可以算出量化噪声的功率谱密度为

(3)

其中fs为给定ADC采样频率.

而真正对采样有影响的是出现在输入信号频率范围内的量化噪声，这部分量化噪声的功率可以通过对功率密度PSD在-fm～fm带上积分来得到

(4)

其中η2为噪声功率，fm输入信号频率.

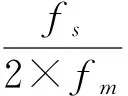
(5)

两边以2为底求对数可得到：

log2η2=-log2OSR-2N-log212+2×log2Vref.

(6)

不进行过采样，即OSR=1，此时

log2η2=-2×N-log212+2×log2Vref.

(7)

若需要提高p位精度，即

log2η2=-2×(N+p)-log212+2×log2Vref.

(8)

由公式(6)和公式(8)可得

OSR=4p.

(9)

即通过4p倍的过采样，能够将原来的数据精度提高p位.

以4p过采样率得到的采样值通过求和、平均的方法进行处理.但是不能将这4p个采样值相加后简单的除以4p，这样只能起到一个低通滤波的作用，R位的采样值经过这样平均后精度仍旧是R位，并不能实现采样精度的提高.数据抽取方法首先将4p个采样值相加，得到一个R+2p位的数值，然后将该数值右移p位，得到一个R+p位的数值，这个数值才是最终提高了p位精度的结果[6].

2.2 实验结果

使用中子发生器控制系统获取储存器电源电压数据，单片机将12位AD转换器的转换二进制结果发送到上位机.在中断处理函数中，单片机将得到的256个数据进行求和，然后右移4位得到一个16位的AD采样二进制值，将其作为过采样结果得到数据如表1所示.

表1 过采样数据结果

由表1中数据可知，在未使用过采样技术的情况下，可以得到12位的测量结果，其每码字对应的电压为：3.3 V/4 096=0.805 6 mV/code；在使用过采样技术后，可得到16位的电压测量结果，其每码字对应的电压为：3.3 V/(4 096*16)=0.050 3 mV/code；因此，使用过采样技术能确实提高电压测量精度.

2.3 过采样前提条件及负荷分析

过采样技术的实现必须满足下面2个条件：

(1) 输入信号里必须存在一些噪音，这些噪音必须是白噪音；

(2) 噪声的幅度必须能够对输入信号产生足够大的影响，以使得ADC转换的结果能随机地翻转至少1位，否则的话将不会带来精度的提高.

而在大多数应用中，内部ADC的热噪声及输入信号本身的变化足以使得以上条件成立[7].根据奈奎斯特采样定律，采样频率必须是输入信号的2倍才能将信号还原，当需要提高p位采样精度的时候，速率又得提高4p倍，STM32上的ADC能达到的最高采样率为1 MHz.过采样技术实质上是通过了大量的数学统计拟合出采样值，大量的数据吞吐增加了CPU的负荷，但是由于STM32F407采用了ARM-Cortex-M4为核心，主频高达168 MHz，因此使用该技术不会给CPU增加太大的负荷.

3 非线性校正

中子管电参数通过采样电路并经过主控芯片处理后送上位机显示，如图3所示.由于采样电路中的电子元器件产生温漂、增益和时漂，例如：模拟运算放大器、电光耦合器等.以往的中子发生器控制台，使用了两点校正的算法对数据做了一定的非线性校正，分析实验数据后发现：选取的两点校准点是否合适对最终的测量数值有较大的影响，在实际应用中，最佳的两点不易寻找[8-10].因此，本文使用最小二乘法对采样数据进行线性拟合，实验测试表明：拟合之后非线性误差为 0.2%.

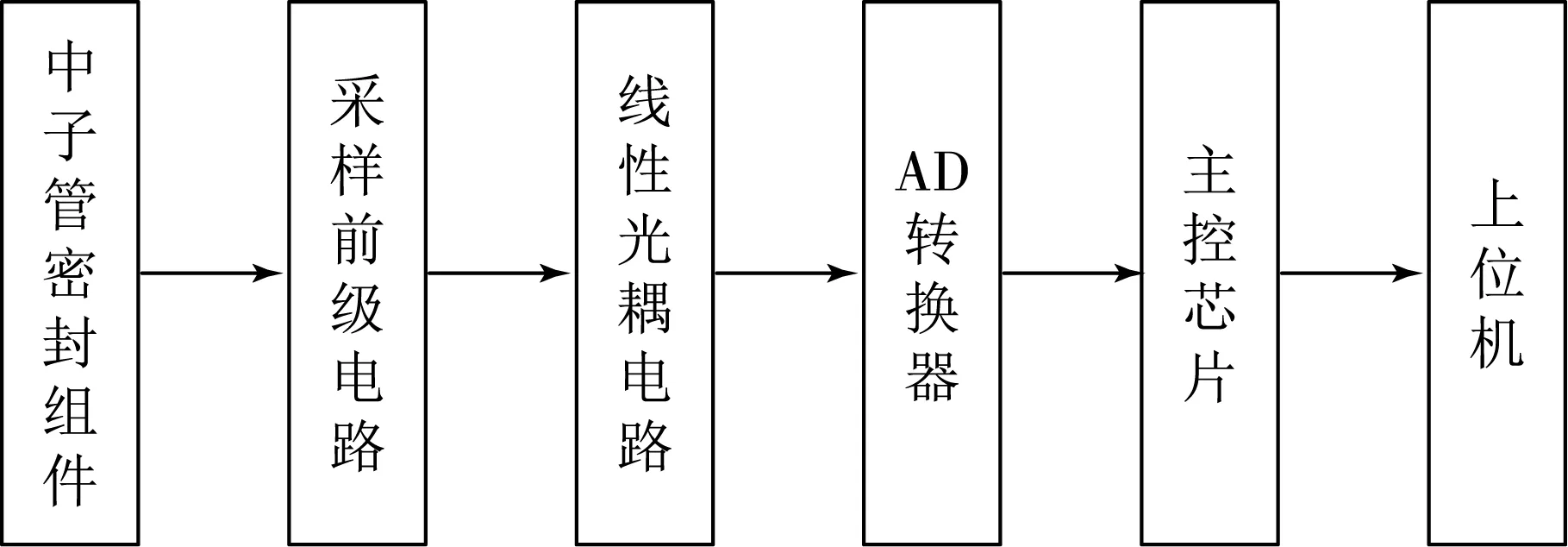
图3 中子管电参数采集示意图

3.1 采样电路实验分析

实验使用了高精密电源模拟中子管电参数作为输入值，上位机显示数值为测量值，测量数据输入值和测量值比较如表2所示.

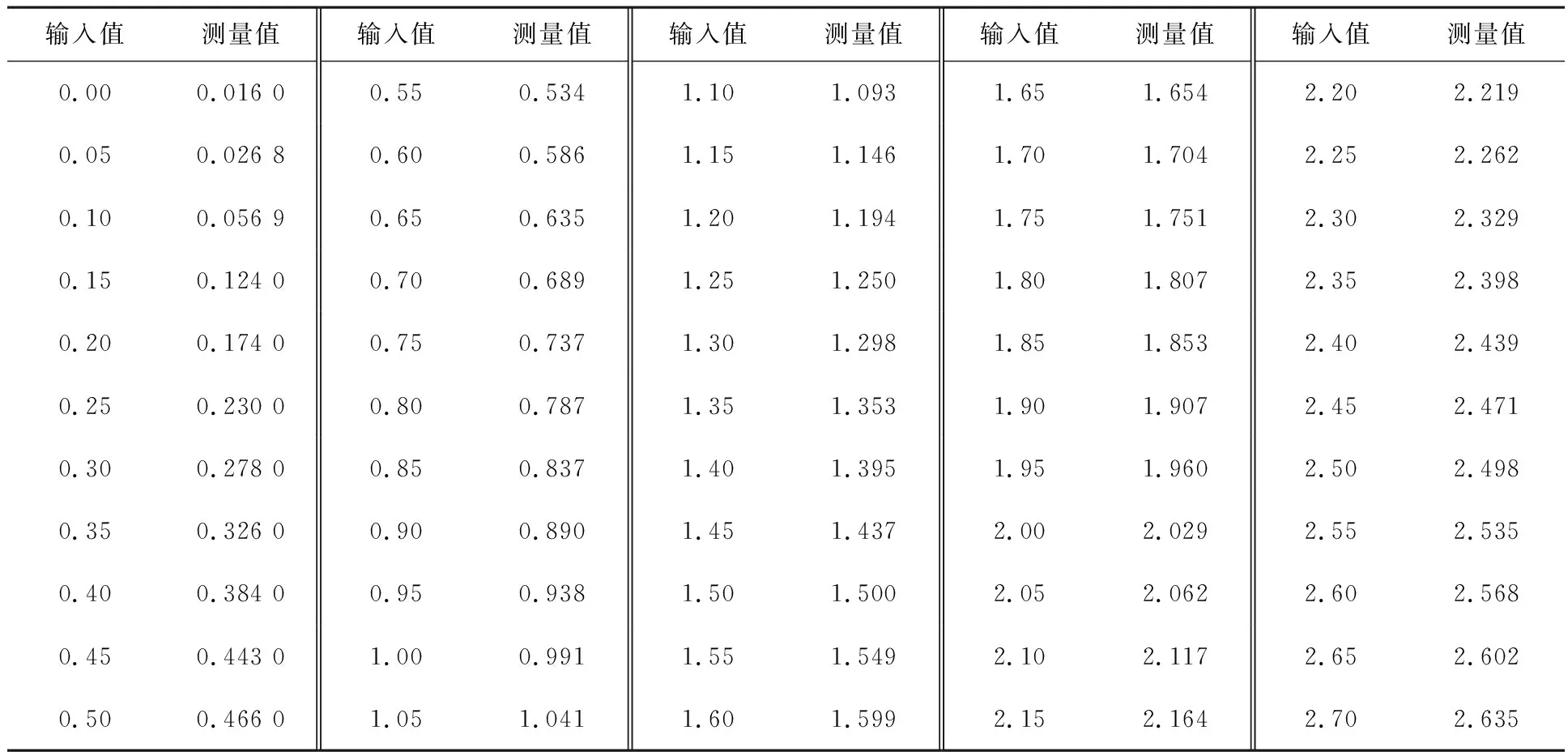
表2 输入值与测量值比较 V

表2中的数据可以通过MATLAB绘制出实际图形如图4所示.图形大致趋势显示成线性增长，因此使用一元线性回归的最小二乘法对其进行线性拟合.

3.2 最小二乘法

数据拟合的原理是：给定一组观测数据(或散点等) (xi，yi)(i=1，2，3，…，m)，在某一类曲线中寻找一条最佳曲线y=φ(x)，最佳的标准是使总体误差最小.如果采用绝对误差，数学上采用微积分知识求最小值不容易处理，因此通常采用最小二乘法来处理.

对于第i个x的值，估计的回归方程可表示为

(10)

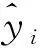
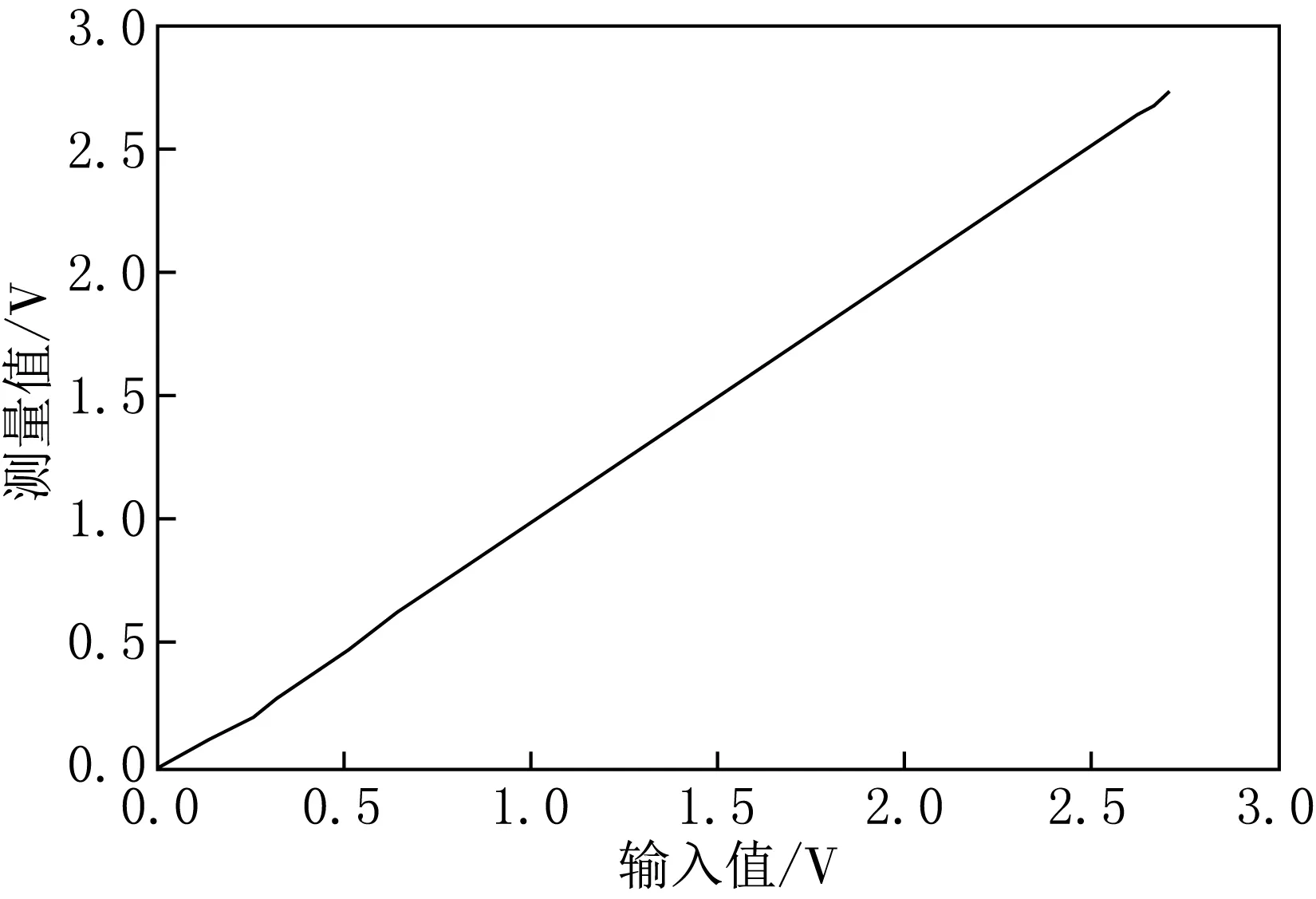
图4 输入值与测量值关系曲线

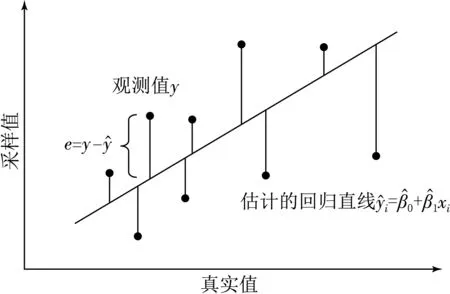
图5 最小二乘法示意图

根据最小二乘法，使

(11)

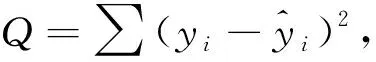
(12)

解得上述方程组得

(13)

3.3 拟合结果及误差分析

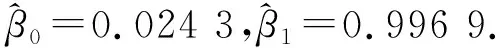
表3 输入值、测量值及误差比较 V

图6 最小二乘法校正后曲线

采用最小二乘法对所测数据进行拟合，得到的输入值与观测值的关系如图6中的虚线所示.

相对误差的定义：即测量的绝对误差与被测量真值之比乘以100%[13]，其定义公式为

(14)

其中：Δ为绝对误差，即测量值-真实值；L为真实值；δ为相对误差.平均相对误差为该组全部相对误差的平均值.

非线性误差定义：拟合直线的线性度(即非线性误差)为测量曲线与拟合直线的最大偏差和满量程输出的百分比，其定义公式为

(15)

其中：ΔYmax为最大偏差；Y为满量程，本实验中数值为3.3 V；ζ为非线性误差.

由表3、公式(14)和(15)可知：实验最大偏差ΔYmax=0.006 V；非线性误差ζ=0.2%；平均相对误差δ=0.023%.

4 结论

本文在大量实验数据的基础上，以ARM-Cortex-M4为硬件平台.根据主控芯片和主控电路的特点，提出了使用过采样的算法来提高AD采集的分辨率.摒弃以往的两点校正法，运用最小二乘法进一步减小了由硬件电路产生的非线性误差.能够在实际中子发生器实验中得到更加精确的中子管电参数.进而能够准确掌握中子管的实时状态，给实验人员提供准确控制依据.实验结果表明：采用过采样技术和最小二乘法能大幅提高AD采集的分辨率和采样电路的线性度.拟合后非线性误差为0.2%，完全符合中子发生器控制台精度要求，为日后的自动控制奠定测量基础.