外磁场对Casimir效应的影响

关仙为，龙玉梅，巴合提古丽·阿斯里别克，刘辉，罗筱璇，张 雪，郑泰玉

(1.东北师范大学物理学院，吉林 长春 130024； 2.新疆伊犁师范大学电子与信息工程学院，新疆 伊犁 135000)

零点涨落是电磁场量子描述的一个显著特点，也是真空中导体板之间的Casimir力和原子与导体板之间的Casimir-Polder力产生的根源[1-2].此后科学家又做了很多有益工作，包括将Casimir-Polder力广泛应用在物理精密仪器及在不同材料中，如金属、石墨烯[3]、超导材料[4].

Casimir力在纳米结构材料中发挥了重要作用，2013年Thompson提出利用聚焦的光学镊子束[5]捕获单个Rb原子，并将其耦合到固态器件上，即纳米级光子晶体腔.该装置也可用于测量基态原子和导体板之间的Casimir-Polder力.2018年科学家研究了原子与石墨烯片之间的Casimir-Polder相互作用及与环境的热平衡理论[6]，并基于非零温度下量子电动力学原理，给出了Casimir-Polder自由能和力的表达式.

区域Ⅰ充满电介质；区域Ⅱ真空态图1 理论模型示意图

近年来越来越多的科学家研究排斥力，希望能够克服纳米技术中的静摩擦问题.理论研究已经发现了3种可以实现排斥力的方法，其中2种已经被实验所证实[7-8].第3种方法要利用磁场获得[9]，但是没有实验能够证明.为了在理论上证明第3种方法，本文选择不受电场影响，在磁场作用下得到自旋能级分裂的中子，将其放在一维介质腔中，如图1所示.本文首先得到腔壁之间Casimir力的表达式，然后通过改变参量研究外部磁场大小、腔长、中子在腔中位置对力的影响.

1 理论模型

如图1所示，本文将一个受外部磁场调控的中子置于腔中位置x0处，x<0空间内充满透明的电介质，x>0空间内为真空.腔的两端x=-l和x=L(L→∞)处分别放置理想导体板，且在x=0处没有涂层，允许其两边的场相互耦合[10].主要研究初态为裸基态时腔壁之间的动态Casimir力.

哈密顿量写成

H=HN+HF+HI.

(1)

其中HN是中子的自由哈密顿量，在外部磁场的作用下中子的自旋态发生分裂，因此中子的自由哈密顿量可以写成

(2)

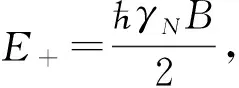
用HF表示有介质存在时的电磁场哈密顿量，公式为

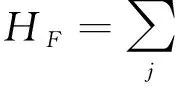
(3)

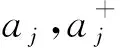
(4)

这样相互作用哈密顿量的表达式为

(5)

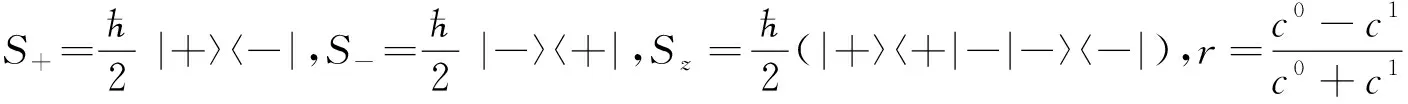
2 腔壁之间的Casimir力

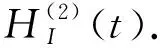
(6)

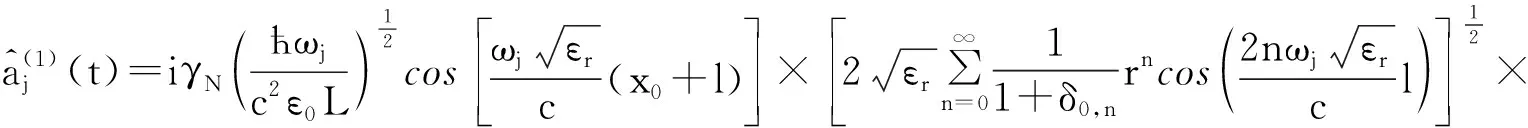
(7)

(8)

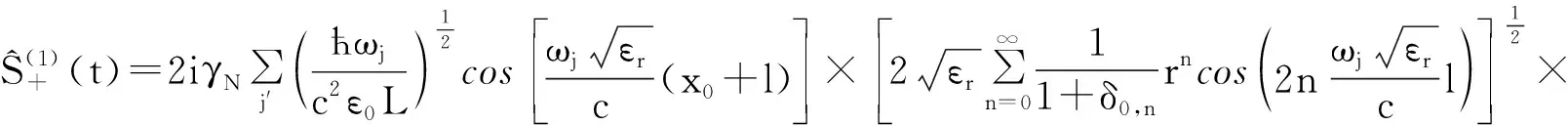
(9)

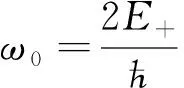
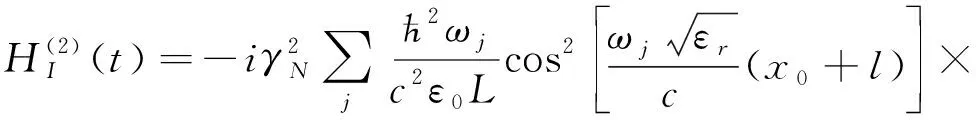
(10)

运用微扰理论计算初态为裸基态系统的二阶能移为

(11)

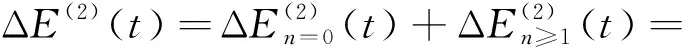
(12)

(13)

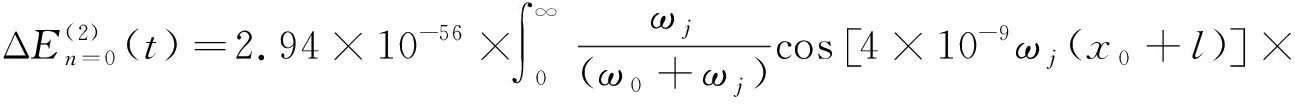
(14)

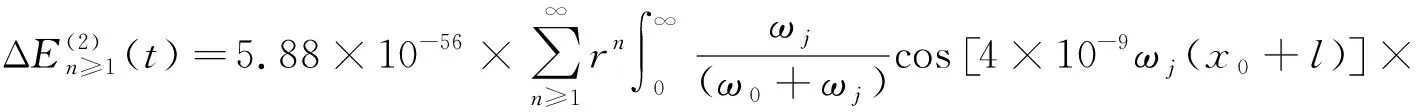
(15)

通过求能量的导数得到腔壁之间的Casimir力为

(16)

将(13)—(15)式代入到(16)式中，得到外磁场影响下的腔壁之间的Casimir力的表达式

(17)

其中：

(18)

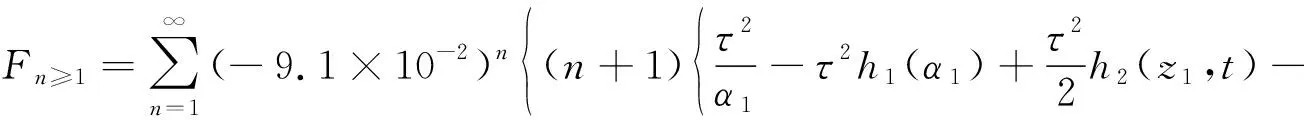
(19)

用Si(x)和Ci(x)分别表示正弦积分函数和余弦积分函数[15].并引入辅助函数：

(20)

h2(x，t)=sin(x)[Ci(x+ω0t)+Ci(ω0t-x)]+cos(x)[Si(x+ω0t)-Si(ω0t-x)]；

(21)

(22)

(23)

3 Casimir力的讨论

为了进一步研究在外磁场作用下，含有中子的一维介质腔腔壁之间Casimir力的特点以及中子位于腔中的位置和微腔尺寸对力产生的影响，进行数值分析.

不同腔长情况下力随磁感应强度大小变化关系示意图见图2.图2中子在腔中位置x0、相对介电常数εr取固定值，微腔长度l取不同值.从图2中可以看出该力为正值，即为排斥力，且随着磁感应强度的增大，力逐渐增大.这说明磁场对该力的大小有调控作用.在磁感应强度大小相同时，微腔的长度越小，力的数值越大.可以推测当腔的长度足够长时，由电磁场的零点涨落引起的Casimir力将会消失.

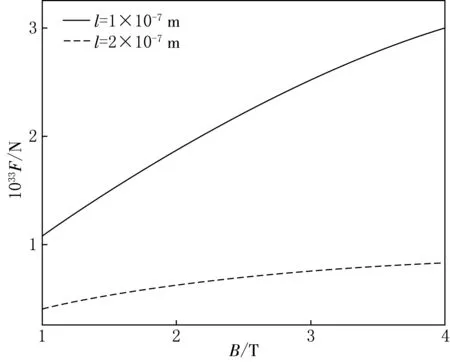
x0=-0.5×10-7 m，εr=1.44，t=1×10-13 s图2 不同腔长情况下力随磁感应强度大小变化关系示意图

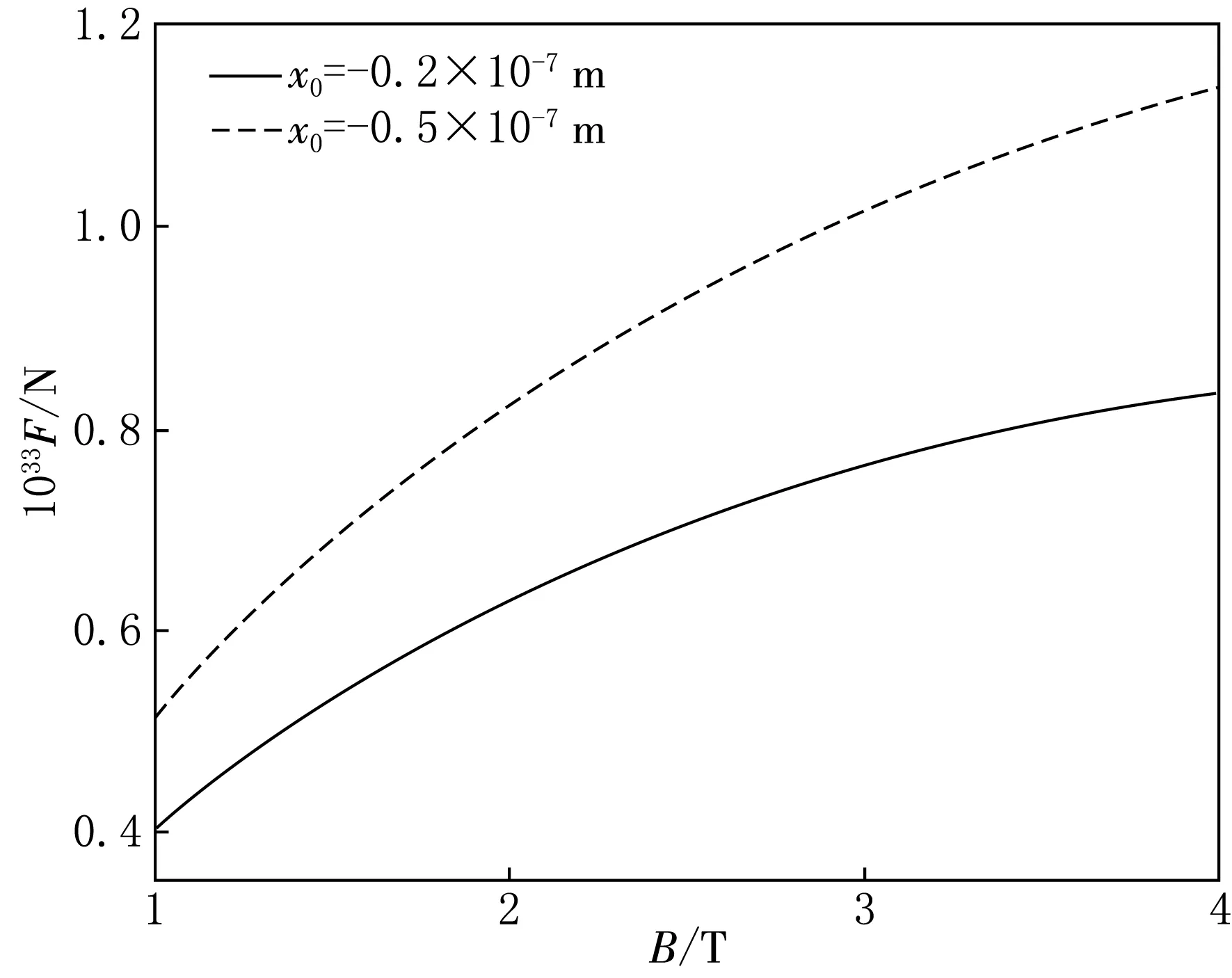
=2×10-7 m，εr=1.44，t=1×10-13 s图3 中子位于腔中不同位置情况下力随磁感应强度大小变化关系示意图

图3表示微腔长度l、相对介电常数εr取固定值，中子在腔中位置取不同值的情况下力随磁感应强度大小的变化趋势.由图3可知，力仍随磁感应强度的增大而增大.磁感应强度相同时，x0越小，即中子越靠近x=-l处的理想导体板，力的数值越大，这与二能级原子与腔壁之间的Casimir-Polder力的相关结论是相似的[16].

4 结论

本文在海森堡表象中运用微扰理论得到含有中子的一维介质腔壁之间的Casimir力[17].通过数值分析得到了不同因素对力的影响.结果表明，腔壁之间的力是排斥力，其大小受到外部磁场的调控，且随微腔长度的增加而减小.这说明中子距离理想导体板越近作用力越明显.该结果为实验中测得Casimir力提供了理论参考.