砖夹-砖块系统的传力机制及夹砖数量研究*
林远东,宫能平,刘丹丹,卢小雨,崔智丽
(安徽理工大学,安徽淮南 232001)
夹具对工件起定位和夹紧的作用[1],图1所示夹持系统为文献[2-4]分析工人用夹具夹砖的力学模型.夹具对砖块的夹持作用及砖块间相互作用力的传递规律,为设计装载机械的夹持系统提供了力学计算的理论依据[2].因而,弄清砖夹-砖块夹持系统内部的传力机制,以及确定影响夹具夹砖数量的影响因素具有重要意义.
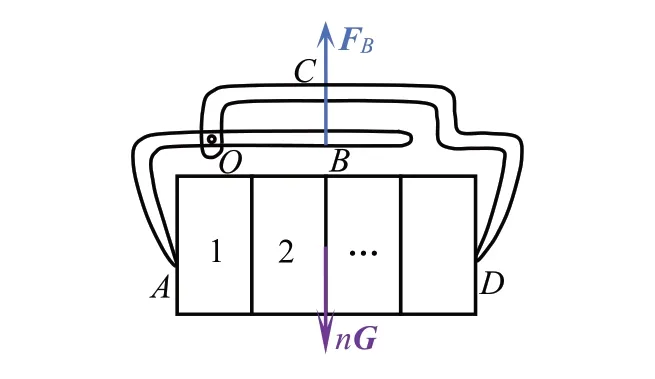
图1 砖夹-砖块系统示意图
在文献[2-4]中,将砖夹自重忽略,并将砖夹和砖块视为刚体.因砖夹的重量较砖块重量小得多,则忽略砖夹自重是合理的.然而,将工人对砖夹的提拉力作用位置处理为AB 构件上的B点,而视OD构件为二力构件,这显然与砖夹的工作原理不符.
图1 中,G 为单块砖头的重量,N;FB为工人作用于AB 构件B 处的提拉力,N;n 为夹具所夹持的砖块数量.
工人手握砖夹工作时,AB 构件和OD 构件均被手握住,构件OD 不但在O 和D 处受力,在C 处还受到手的抓握力,故OD 构件不是二力杆.另外,文献[2]将砖夹夹持砖块系统的位置认定为砖块高度的一半处也欠妥.
因此,笔者对砖夹-砖块系统的计算模型进行了修正,应用静力学平衡理论和摩擦库伦定律分析了砖夹-砖块夹持系统内部的传力机制及确定了砖夹所能夹起砖块数量的问题.研究结果不但为设计装载机械的夹持系统提供了力学计算的理论依据[2],还进一步加深了对静滑动摩擦和静力学平衡理论等知识的理解.
1 修正的砖夹-砖块系统模型
手握夹具工作时,手臂哪怕使出大于夹具所夹砖块重量的提拉力,砖块也未必能被夹起,当夹具对砖块的夹持作用不够大时砖块将发生滑脱现象.
夹具对砖块的夹持力,其力源为手对夹具的抓握力.当手对砖夹的抓握力足够大时,夹具便能夹住砖块;若砖块不发生滑脱,工人能否提起砖块则是由手臂的提拉力所决定,当手臂的提拉力大于砖块重量时工人便可将砖块提起.
因此,除了手臂的提拉力之外,手对砖夹的抓握力也是能否提起砖块的一个关键因素.手对夹具的抓握力会因人而异,其与手臂提供的提拉力没有关系;而且,即使是同一人,因其握紧夹具的程度不同,手对夹具的抓握力也会不同.
手对夹具的抓握力具有3个特征:在B点处受到由B指向C方向的力;在C点处受到由C指向B方向的力;B点和C点所受力的大小相等.
根据手对夹具的抓握力特征,作用在夹具上B 点和C 点这两处的力大小相等、方向相反且力线重合,则可将手对夹具的抓握作用等效为一个连接在B 和C 之间的受拉弹簧.务必注意,由手对夹具的抓握力的特征可知,连接在B和C间的弹簧只能受拉.从而,将文献[2-4]中(图1所示)砖夹-砖块系统的力学模型修正为图2所示的情况.
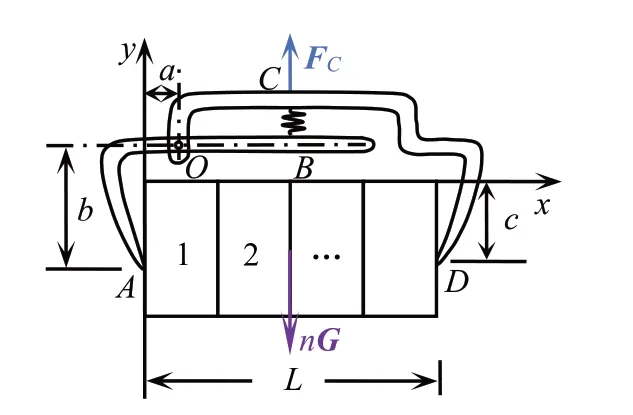
图2 修正的砖夹-砖块系统示意图
图2 中,FC为手臂对砖夹的提拉力,N;a,b 和c 分别为夹具到砖块位置参量,m;L 为夹持宽度,m;其余各量同上.
设单砖的宽度和高度分别为b0和h,则由图2可见:

对于砖夹-砖块系统,由平衡得:

由式(2)得手臂对砖夹的提拉力为:

由式(3)可见,在砖夹自重忽略不计的情况下,当工人用砖夹夹砖时,其手臂对砖夹的提拉力大小为被夹砖块的重量.
2 砖夹对砖的作用及手的抓握力
夹持系统中,受夹砖块系统的受力情况如图3(a),而构件AB的受力情况如图3(b).
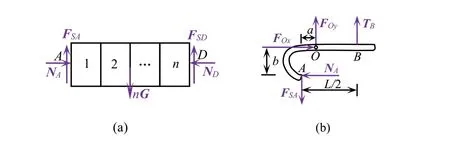
图3 砖夹-砖块系统的内力分析
图3中,NA和ND为夹具对砖块系统两侧的正压力,N;FSA和FSD为夹具对砖块系统两侧的静滑动摩擦力,N;FOx和FOy为构件AB在铰接点处所受约束力,N;TB为手对构件AB的抓握力,N.
2.1 砖夹对砖块系统的作用
对于受夹的砖块系统,由平衡得:

由式(7)可知,砖夹作用于砖块系统两侧的正压力是相等的.
由式(7)可知,砖夹作用于砖块系统两端的静滑动摩擦力相等.
由摩擦库伦定律[4]可知:
式中,FSmax为砖块系统在夹持点所受最大静滑动摩擦力,其值为:
式中,fS为砖夹与砖块间的静摩擦系数.
2.2 手对砖夹的抓握力
由式(8)和式(12)得砖夹对砖块的正压力NA与手对砖夹的抓握力TB之间的关系为:

式(13)表明,砖夹对砖块的正压力与手对砖夹的抓握力呈线性关系,且夹具对砖块系统的正压力随着手对砖夹抓握力的增大而增大.
由式(11)和式(13)得砖块相对于夹具不发生滑脱时手对砖夹的抓握力TB需满足的条件为:

综上,砖块不发生滑脱现象,关键因素取决于手对砖夹的抓握力的大小.
3 砖块在接触面上的相互作用力
自受夹砖块系统中从左往右取j块砖为研究对象,分析第j块砖的右侧面受第j+1块砖左侧面施加的作用力.
第j 块砖右侧面上各点具体的受力情况如何,我们是不清楚的.然而,无论其如何分布,我们可由力系等效与简化理论以及砖块系统在力系作用下保持平衡的状态,将第j块砖右侧面上所受约束力简化和等效为一正压力和与面相切向下的摩擦力作用,设力的作用点距砖块上面的距离为ej,如图4所示.
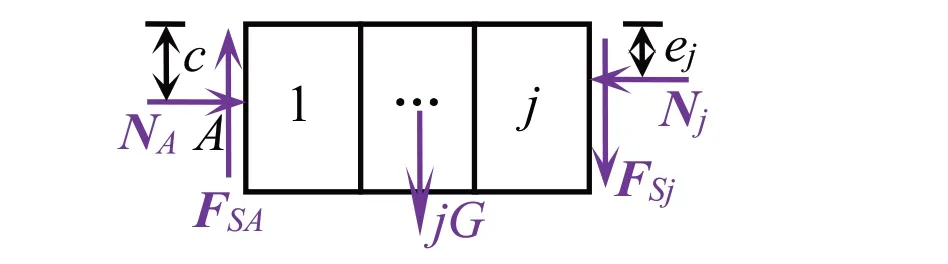
图4 受夹砖块在接触面上的相互作用力分析
图4中,Nj和Fsj分别为第j块砖受第j+1块砖作用的正压力和静滑动摩擦力,N;ej为第j块砖受第j+1块砖作用的等效力作用点距砖块上方的尺寸,m;j为砖块的位置编号,为自然数,且jϵ[1,n].
当j 取n 时,Nj和Fsj表示图3(a)中砖块系统在夹持点D 的受力情况,则受夹砖块系统内部砖块在接触面上相互的作用力,其需满足的边界条件为:

对于图4所示的砖块系统,由静力学平衡得:

3.1 各砖块在接触面上的正压力
结合式(7)可知,Nj=ND.由此可见,式(19)满足式(15-1)表示的边界条件.式(19)表明,受夹砖块系统内部各砖块在接触面上相互作用的正压力大小相同.
3.2 各砖在接触面上的静滑动摩擦力
由式(8)和式(17)得第j块砖头受第j+1块砖的静滑动摩擦力Fsj为:
当j取n时,由式(20)得FSn=-nG/2,这说明该界面上实际所受静滑动摩擦力的指向与图4所示相反,即实际为向上方向,与图3(a)所示情况完全一致.因此,式(20)满足式(15-2)表示的边界条件.
由式(20)可知,砖块系统内各砖块在接触面上所受静滑动摩擦力呈现先减小后增大的趋势.从而,受夹砖块系统中存在静滑动摩擦力取得最小的接触面,该最小静滑动摩擦力的具体情况为:
(1)当砖块数n为偶数时,砖块系统内的砖块在相互接触面上有静滑动摩擦力为0的情况.此时,由式(20)得j=n/2,即第n/2块砖与第1+n/2块砖在接触面上没有静滑动摩擦力的作用;
(2)当n为奇数时,j=n/2不是整数,故第(n+1)/2块砖的两侧面静滑动摩擦力最小.将j=(n+1)/2代入式(20),可得砖块数n为奇数时,砖块系统内部的砖块在接触面上所受的最小静滑动摩擦力为:
式(21)表明,当受夹砖块系统的砖块数量n为奇数时,正中间的砖块在两侧面上受到的静滑动摩擦力最小,其值为单块砖重量的1/2,负号表示静滑动摩擦力的方向与图4 所示方向相反,即实际指向向上.
3.3 各砖在接触面上受力的作用位置
由式(18)~式(20)得第j块砖受第j+1块砖作用力的等效作用点位置参量ej为

当j取n时ej对应于图3(a)中点D位置,则各砖块在接触面上,正压力和摩擦力的等效作用点应满足边界条件
显然,式(22)满足式(23)表示的等效作用点对应的边界条件.
式(22)表明,第j 块砖受第j+1 块砖作用力的等效作用点位置参量ej是砖块位置编号j 的函数.因ej是j的函数,则由式(22)可得
令∂ej/∂j=0,由(24)可得j=n/2.从而,当j<n/2时∂ej/∂j<0;而当j>n/2时∂ej/∂j>0.结合函数增减性判别准则[5]可知:
(1)当j<n/2时∂ej/∂j<0,表明ej随着j的增大而减小;
(2)当j>n/2时∂ej/∂j>0,表明ej随着j的增大而增大.
因此,ej在j=n/2处取得最小值,该最小值为
4 砖夹能夹起砖块的数量
受夹砖块系统的各块砖之间相互作用力得等效作用位置须在交界面上,则ej的最小值应满足:

砖块系统处于极限平衡状态时,夹具所夹起砖块的数量达最大值.此时,由式(14)可得手对夹具的最小抓握力为
同理,由式(13)和式(27)可得极限平衡状态下夹具作用于砖块系统上的最小正压力为:

注意到,系统处于极限平衡状态时式(28)也可由式(8)~式(10)直接导出.
由式(30)可见,当c=h/2时,砖夹所能夹起砖块的最大数量与文献[2]的结论完全一致.然而,工人夹砖时,砖夹的夹持位置具有不确定性.因此,本文的分析更具有一般性,相应结果具有普适性,文献[2]的结论仅为本文的一种特例.
5 影响砖夹夹砖数量的因素
由式(30)可见,用砖夹能夹起砖块的数量与单砖宽度、砖块与砖夹间的摩擦系数及砖夹夹砖的具体夹持位置有关.其中,砖的宽度及砖夹与砖块间的摩擦系数为系统的确定量;而砖夹夹砖的位置为可变量,砖夹能夹起砖块的数量与夹持点距砖块上面的距离成正比关系.
因此,砖夹夹砖的夹持位置越低,所能夹持的砖块数量越多.然而,砖夹能夹起砖块的数量不仅仅只由上述3个参量确定.
首先,式(30)所确定能夹起砖块的重量是要由工人手臂来承担.因此,工人手臂对砖夹的提拉力要与所夹砖块重量相匹配,在此前提下砖夹方能夹起相应数量的砖块.将砖夹能夹起砖块数量最多时的手臂提拉力记为FCm,则由式(3)和式(30)得:
另外,工人手握砖夹的抓握力要与所夹砖块对应的抓握力相匹配.只有工人手握砖夹的抓握力与所夹砖块数量代入式(27)所得抓握力时,由式(30)确定的砖块数量才有实际意义.将砖夹所能夹起最多砖块数量时工人手握砖夹的握紧力记为TBm,则由式(27)和式(30)得:

因此,砖夹能夹起的砖块数量不仅与单砖的宽度、砖块与砖夹的静摩擦系数及砖夹夹砖的位置有关,还与工人手臂的提拉力以及手握砖夹的最小抓握力有关.
6 结论
(1)砖夹-砖块夹持系统中各砖块在相互接触面上所受的正压力是不变的;而静滑动摩擦力的大小和方向是随砖块处于系统中具体位置的变化而变化的。
(2)砖夹-砖块夹持系统中各砖块在相互接触面上所受的静滑动摩擦力表现为先减小后增大的变化规律;当受夹砖块数n 为偶数时,第n/2 块砖与第(1+n/2)块砖在接触面上相互作用的静滑动摩擦力降低为零;而当砖块数n 为奇数时,第(n+1)/2 块砖的两侧面上所受静滑动摩擦力降低至最小值,其值为单砖重量的1/2。
(3)砖夹-砖块夹持系统中各砖块在接触面上所受正压力和静滑动摩擦力的等效作用点位置,是随砖块处于砖块系统中具体位置的变化而变化的;该等效作用点距砖块上方的距离呈现先减小后增大的变化规律。
(4)砖夹所能夹起砖块的数量不但与单砖的宽度、砖块与夹具间的摩擦系数和砖块受夹位置有关,还与工人手臂对夹具的提拉力和手对夹具的抓握力有关。

