透镜在任意介质中的成像规律研究
吴位巍,陈 亮
(凯里学院,贵州凯里 556011)
光学元件是光学系统的基本组成单元,大部分光学元件起成像的作用,还有一些在光学系统中起特殊作用(如滤波、分光、传像等)的元件,透镜是使用最广泛的成像元件[1].生活中人们经常使用照相机拍照,可以把瞬间情景留为永恒的记忆;利用摄影仪,可以使教室里的同学看到放大的图片;医院化验室的医生,在显微镜下可以看见血液中的各种细胞........这些与我们的生活息息相关的光学仪器,它们的主要部件都是透镜.
透镜是根据光的折射规律制成的,把玻璃、塑料、石英等透明物质磨成薄片,使其两表面都为曲面或一面为平面,即成为透镜,因此,它也可以看成是由两个共轴折射曲面构成的光学系统.透镜有厚薄之分,即薄透镜和厚透镜,从目前的文献资料来看,关于透镜处于任意介质情况下的成像规律还未见报道,本文从成像规律、主点和光焦度等方面来对薄透镜和厚透镜这两个光学元件进行分析.
1 成像规律
由于曲面的大小有一定的范围,使得折射光束的张角范围受到一定的限制,要使通过前一个曲面的光束必须能通过或部分通过次一个曲面,多个曲面的曲率中心必须都在同一直线上[2],即构成一共轴光具组,这条直线称为主轴,包含主轴的任一平面为主平面.
物点发出的单心光束,通过光学系统后仍保持为单心光束,则该单心光束的心为物点的像.光在界面上折射时,单心光束的单心性将被破坏,但在近轴光线条件下单心性能保持[2].
厚透镜的两曲面在其主轴上的间隔即厚度同它的焦距相比不能忽略,在近轴光线条件下它的成像规律可采用逐个曲面成像,以两曲面是球面为例,其主平面内的光线如图1所示.

图1 厚透镜主平面内的光线
厚透镜置于n1和n2介质中,对于AO1B球面,光线的光程为

根据费马原理,光沿光程为最大值、最小值或恒定值的路程传播,有,得
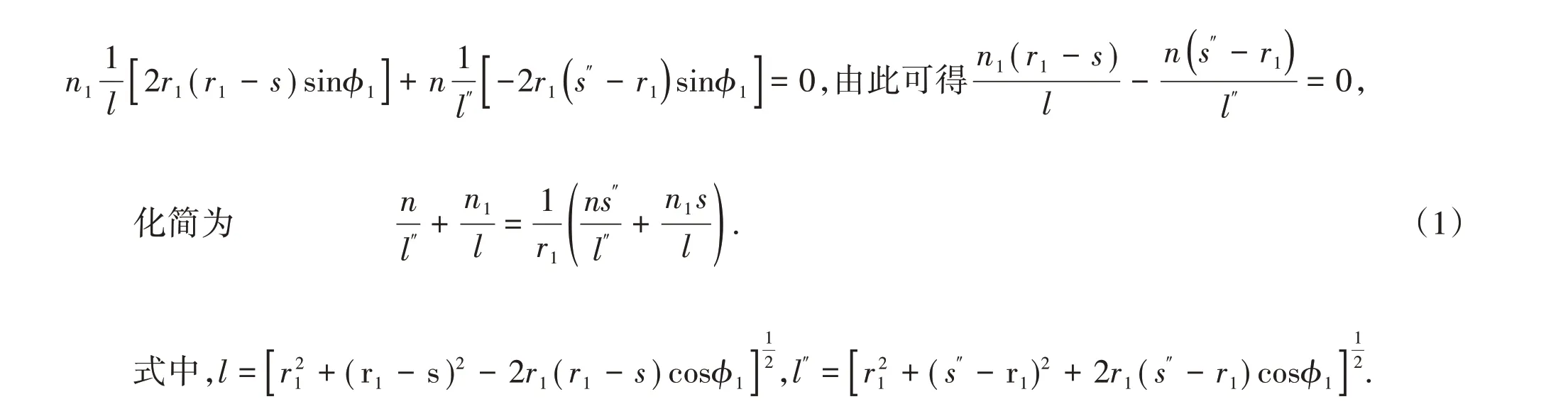
其中n表示厚透镜的折射率,r1表示AO1B球面的曲率半径,s表示物距,s″表示像距.
由(1)式可以看出,s″和φ1的大小有关,说明从物点p 发出的单心光束经球面AO1B 折射后,单心性被破坏.
在近轴光线条件下,φ1的值很小,在一级近似下,cosφ1≈1,因此有

根据符号法则,s的数值为负,s″的数值为正,而l和l″的数值应为正,所以考虑物理量的符号后有

对于AO2B球面,用上面处理AO1B球面的同样方法,可得

其中r2表示AO2B球面的曲率半径,t表示厚透镜的厚度,s′表示厚透镜像的位置.
由(2)和(3)式可得厚透镜的物方焦距f和像方焦距f ′为(2)和(3)式即为厚透镜处于任意介质中时的成像规律.
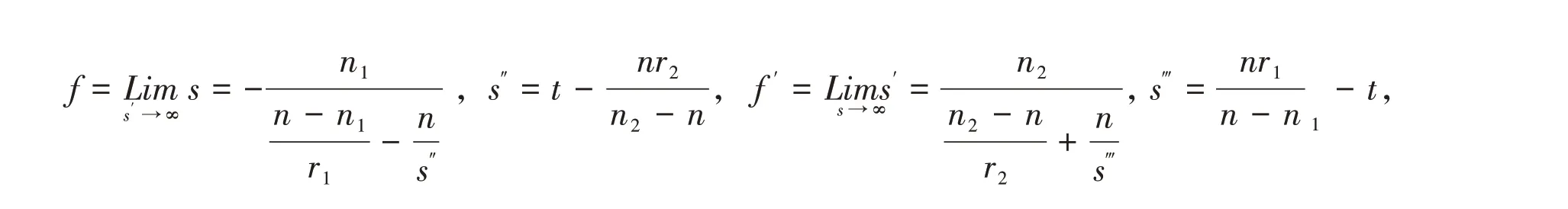
两曲面在其主轴上的间隔即厚度同它的焦距相比可以忽略即为薄透镜,仍以两曲面是球面为例,其主平面内的光线如图2所示.
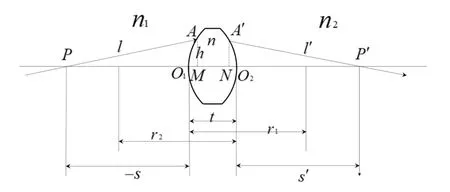
图2 薄透镜主平面内的光线
薄透镜置于n1和n2介质中,任一光线PAA′P′的光程为式中
在近轴光线条件下,Δ2可表示为

在近轴光线条件下,h远小于曲率半径,可略去h2项,而且此时l≈-s、l″≈s″,上式就为
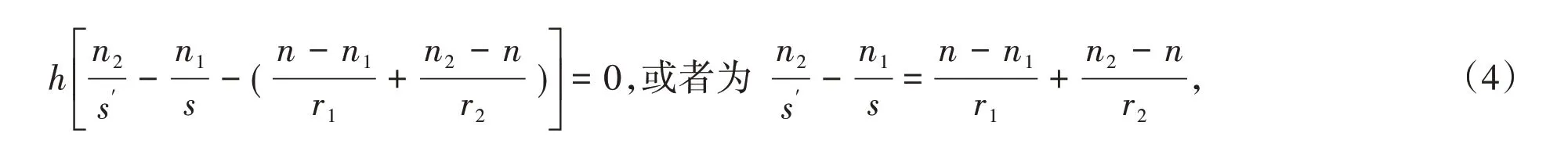
由(4)式可得薄透镜的物方焦距f和像方焦距
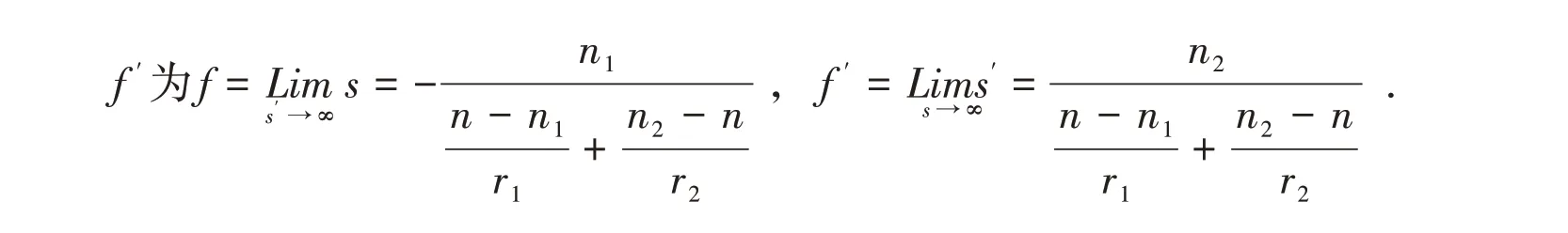
(4)式即为薄透镜处于任意介质中时的成像规律.
另外,当t=0时,由(2)式加(3)式可得,上式与(4)式是一样的,也就是说在特殊条件下由厚透镜的成像规律可以得到薄透镜的成像规律.
2 主点
在(2)、(3)、(4)式中s、s″的起点在顶点o1,s′的起点在顶点o2,物方焦距f是从o1量的,像方焦距f ′是从o2量的,显然,用(2)、(3)、(4)式来决定像的位置是相当复杂的,为简化成像规律为高斯形式,需选择其他的参考点即主点H、H′,如图3所示.

图3 厚透镜的主点
为简化运算,(2)、(3)式改写为


假设物距s和像距s′的起点从顶点o1和o2分别移动p和p′后,起点为主点H、H′的物距、像距满足高斯形式,即
式中f、f ′为厚透镜的物方焦距和像方焦距,起点在H、H′.
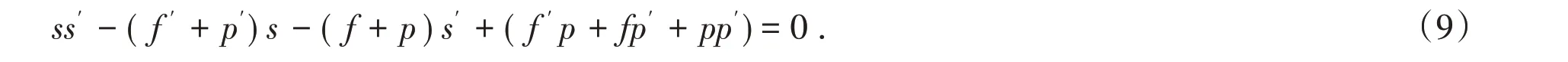
(7)式和(9)式中各项的系数应该相等,即

由以上三式可得任意情况下的厚透镜主点位置.例如,厚透镜处在同一介质中,即n1=n2=n0,由光路可逆原理有再根据符号法则得到f ′=-f,这时上述三式变为

当n0=1时,即厚透镜处于空气中,解上述三式可得

(13)和(14)式给出了处于空气中厚透镜的主点H、H′位置.
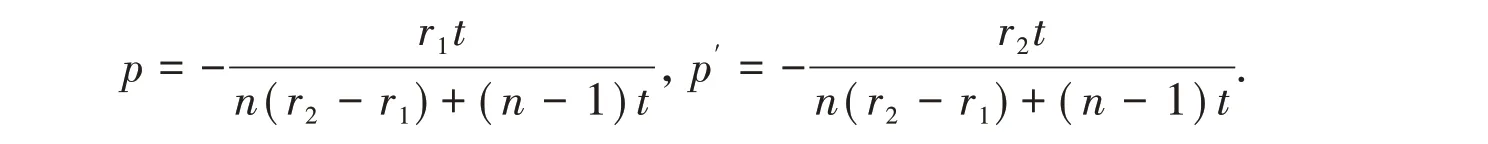
上两式与文献4结果一致.
若是处于空气中的薄透镜,即t=0,由(13)、(14)式可得到它的主点H、H′位置为p=0,p′=0即处于空气中薄透镜的主点H、H′与顶点o1、o2重合.
3 光焦度
光焦度Φ 是表征光学元件聚焦特征的物理量,反应光学元件偏折光线的能力,Φ>0 表征光学元件有聚焦作用,Φ<0表征光学元件有发散作用,Φ=0表征光学元件既没有聚焦作用又没有发散作用,Φ 的绝对值越大光学元件对光束折得越厉害.光焦度等于像方光束汇聚度与物方光束汇聚度之差,即[3]
其中f ′为起点在H′的像方焦距,f为起点在H的物方焦距,n′为像方折射率,n为物方折射率.
对于厚透镜,只要从(10)、(11)、(12)式得到f ′或f,再由(15)式就可知道处于任意介质情况下厚透镜的光焦度Φ.如处于空气中的厚透镜,将(13)、(14)式代入(10)、(11)、(12)式,同时考虑到此时f ′=-f,得f ′=
(16)式与文献3中关于处于空气中厚透镜的结果是一致的.另外,当t=0时,由(16)式有Φ=Φ1+Φ2.
上式说明,处于空气中薄透镜的光焦度等于构成薄透镜的两个折射曲面光焦度之和,这与文献5中的结果相同.
通常情况下,无论是厚透镜还是薄透镜均不能成像,只有在近轴光线条件下才能保持光束的单心性成像,若以球面顶点o1和o2为起点,两种透镜的成像规律形式不一样,分别为(2)(3)、(4)式,但若以主点H和H′为起点,两种透镜的成像规律都是高斯形式,即(8)式;处于任意介质情况下,两种透镜的物方焦距和像方焦距大小不等,只有在同种介质中大小才相等;虽然透镜可以看成是由两个共轴折射曲面构成的光学系统,但它的光焦度并不完全由两个折射曲面的光焦度决定,只有在空气中的薄透镜,它的光焦度等于两个折射曲面的光焦度之和.

