含相变材料热结构拓扑优化研究 *
张晓亮,于江祥,刘昌洪
(北京电子工程总体研究所,北京 100854)
0 引言
随着现代工业的迅猛发展,包括能源、石油化工、航空航天在内的诸多领域的设备及构件常常需要在高温环境下进行工作,然而由于材料性能受温度影响,当结构温度超过使用温度极限时,会使结构的强度、刚度以及可靠性下降。所以,针对高温环境下工作结构的热适应或热防护设计是十分重要的[1]。
针对热环境的适应性设计主要有被动式、半被动式和主动式3种[2]。具体采取何种形式需要根据环境特点、工作时间、结构要求,效率、复杂性、可靠性、综合成本等多方面考虑。从原理上看,被动式结构相对简单,主动式热防护方案结构复杂,难于制造,需要一个额外的冷却剂泵送系统来维持冷却,系统复杂度较高;半被动式的烧蚀结构难以满足保形需求,而热管结构的加工难度较大、加工成本高且技术成熟度较低,所以,如何提高被动式防热结构的热防护能力依然是目前工程上的重要关注方向。
一定热载荷条件下,结构的升温速率主要由材料的热沉与导热系数决定,若需要减缓承力部位在工作过程中的升温速率,使其在更长时间内保持一定的承载能力,则需要进一步增加局部质量来提高局部热沉。但常用的高强度材料储热密度普遍较低,在轻量化要求的限制下难以达到预期的效果。而一般物质在由固相变为液相时会吸收热量,并且在相变过程中,温度一直保持在相变点,直到相变结束,这一过程吸收的热量往往十分可观。
铝基相变材料导热率高,储热密度大,相变体积变化小,且资源丰富,具有较高的性价比,是当前研究最为广泛的金属相变储热材料[3]。而且,铝基相变材料的相变温度在450~571 ℃,与工程中常用的TA15钛合金的使用温度相匹配,短时使用温度可达800 ℃,是一类与钛合金结构适应性较好的相变储热材料。目前研究较多的铝基相变材料的相变潜热分布在310 000~560 000 J/kg之间[4-5],而钛合金的比热容为545 J/(kg·K),这也就意味着铝基相变材料的熔解热至少相当于将相同质量的钛合金加热升温568 ℃吸收的热量。因此,如果在钛合金结构中加入铝基相变材料,不仅可以高效的提高结构热沉,而且当结构中的相变材料开始发生相变时,由于其温度在相变结束前一直维持在相变点,一段时间内会在局部形成低温区,从而延缓钛合金温升的速率,使钛合金结构可以更长时间的在使用温度以下工作。
所以,本文利用铝基相变材料导热率高、储热密度大且相变温度与钛合金使用温度相匹配等特点,从提高结构工作时间的角度出发,基于非梯度拓扑优化方法KG-MFSE(Kriging-based material-field series expansion topology optimization algorithm)[6],构建了加热状态下考虑相变传热过程的截面热刚度拓扑优化模型,以热载荷作用下某时刻截面抗弯刚度最大为优化目标,对某一承受弯曲载荷的异质加强筋截面进行了拓扑优化研究,基于2种单位质量储热量较大的铝基相变材料,进行了加强筋截面的拓扑优化设计,达到了减缓加强筋部位升温速率,延长其工作时间的目的。
1 KG-MFSE拓扑优化方法[6]
相变材料的热物性参数随温度变化,具有强烈的非线性,所以考虑相变传热的拓扑优化问题的灵敏度计算必须利用差分法进行求解,需进行大量的有限元分析,十分耗时[7-8]。
近期,大连理工大学罗阳军教授与亢战教授团队提出了一种基于Kriging代理模型的非梯度拓扑优化方法KG-MFSE,该方法基于随机场的级数展开理论[8-9]提出了一种新的拓扑描述方法,在保证结构描述精度的前提下,实现了拓扑优化问题中设计变量数目的大幅缩减,通过50~100个设计变量控制了设计域中的拓扑变化,结合设计域的自适应调整策略,可高效地进行拓扑优化问题的求解。
利用KG-MFSE方法进行考虑相变传热过程的结构拓扑优化设计可避免耗时的灵敏度分析过程,故本文基于KG-MFSE方法进行考虑相变传热的拓扑优化。
1.1 基于材料场级数展开的拓扑描述方法[10]
材料场函数在设计域中具有一定的连续性。将材料场视为具有预定义边界的未知场,可以通过空间中各点的相关性描述这种连续性。为确定设计域内的材料场函数,首先需要设置Np个在设计域中均匀分布的观测点{x1,…,xNp},基于这组观测点便可得到定义在设计域上的相关性矩阵C。
(1)
式中:C(xi,xj)为空间中两点xi与xj的相关性大小,其值可根据指数形式的距离相关函数计算得到,如式(2)所示。
(2)
式中:lc为材料场中的相关性长度,lc越大,材料场中各点的相关性越强。对于设计域为矩形(短边长度为b)的拓扑优化问题,一般可取lc=b/3,便可以在优化结果中得到主要的拓扑特征。求得设计域中的相关性矩阵C之后,便可根据式(3)定义设计域内的材料场函数。
(3)
式中:η=[η1,η2,…,ηM]T是材料场函数中的待定系数,即拓扑优化问题中的设计变量;M则为待定系数η的维数,其取值可由式(4)确定;Cd(x)为设计域中坐标点x与设计域中各个观测点的相关性向量,其中各元素的值同样可由式(2)决定;Λ为由相关性矩阵C中降序排列的前M个特征值组成的对角线矩阵,Φ为相应的M个特征向量组成的矩阵。
(4)
式中:λj(j=1,2,…,Np)为以降序排列的相关性矩阵的特征值;Np为设计域中观测点的数目;ε>0为材料场函数的容许截断误差。
1.2 材料插值模型
根据任意位置x处材料场函数φ(x)的值,便可以得到材料在设计域中的分布情况:

(5)
不过,直接由式(5)构建的拓扑优化问题是高度非线性和病态的,为改善拓扑优化问题性态,引入了Heaviside函数进行材料场函数φ(x)与拓扑结构的映射:
(6)

为进行有限元模型的拓扑描述,引入相对密度的概念:
(7)
式中:ρe和xe分别为单元e的相对密度与中心位置;ρmin为单元的相对密度下限,以避免有限元分析过程中出现奇异问题,文中取ρmin=0.001。
基于相对密度ρe与SIMP材料插值模型[11],优化过程中各单元的物性参数可由下列等式确定:
弹性模量:
Ee=EA+ρe(EB-EA),
(8)
焓值:
(9)
单元质量:
me=mA+ρe(mB-mA),
(10)
热导率:
(11)
式中:下标A,B分别表示A,B 2种材料,本文中A表示TA15,B表示铝基相变材料。
1.3 设计空间自适应的Kriging代理模型辅助优化算法
基于设计空间自适应调整策略的代理模型优化算法的基本流程为:首先确定初始子设计空间,通过实验设计的方法在子设计空间中抽样得到初始样本并计算其响应值构建初始Kriging代理模型[12],然后开始在当前子设计空间中的迭代寻优,在每一次的迭代过程中选取使更新准则函数值最优的点作为更新点,并计算更新点的真实响应值,更新代理模型,然后进入下一次迭代,直到子迭代的终止条件被满足,停止在当前子设计空间中的寻优,以当前样本集中的最优样本作为下一个子设计空间的中心点,更新子设计空间,开始在新子设计空间中的迭代寻优,直到整个优化过程的终止条件被满足,优化结束。
子设计空间自适应调整策略的数学列式如下[6]:
Ωk=|η-ηk|∞≤rk,k=0,1,2,…,
(12)
(13)
rk+1=0.95rk,
(14)
式中:Ωk为第k次子优化问题的设计空间;rk为第k次子优化问题中设计空间的半径;ηk+1为第k次子优化得到的最优样本,也是第k+1次子优化问题中设计空间的中心。
在子设计空间中优化的终止条件为
EI(ηk)≤0.01·yminorNk>50,
(15)
式中:EI表示改善期望函数[12];ymin为样本集中最优样本的目标函数值;Nk为第k次子优化过程中更新样本点的次数。
在本文中,整个优化过程的终止条件为
|ηk+1-ηk|∞≤0.01.
(16)
2 含相变材料加强筋截面拓扑优化
薄壁加筋或骨架蒙皮结构中,加强筋是主要承力元件,如图1所示,具有较高的强度要求,又由于加强筋局部热容较小,在高温环境下升温迅速,是结构热控设计中需要重点关注的部位[13]。所以本文以某一在热载荷作用下承受弯曲载荷的加强筋的截面作为研究对象,进行含相变材料结构的优化研究。

图1 轻量化结构中的加强筋Fig.1 Stiffeners in lightweight structures
2.1 优化问题说明
本文研究的加强筋截面如图2所示,筋高24 mm,凸缘宽度12 mm,厚度为3 mm,所用材料为钛合金TA15,由于整个模型的对称性,故在研究中只取整个结构的1/4。由于加强筋在工作过程中主要承受弯曲载荷,抗弯刚度是评价其承载能力的重要指标。
基于Euler-Bernoulli梁理论,梁的抗弯刚度可表示为截面二次矩与弹性模量的乘积,其离散形式为[14]
(17)
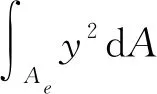

图2 加强筋截面与拓扑优化设计域Fig.2 Stiffener section and topology optimization design area
当截面受到瞬态热载荷作用时,截面中不同区域的单元体具有不同的温度,而材料的弹性模量随温度的变化而变化[15],表1为不同温度下TA15的弹性模量。

表1 TA15的弹性模量[16]Table 1 E of TA15[16]
所以考虑瞬态热载荷作用时的截面抗弯刚度的计算公式为
(18)
由表1中的数据可以看出,温度对于材料的弹性模量具有较大的影响,而且目前可查到的TA15弹性模量数据只给到了550 ℃,是TA15推荐使用温度范围之内的数据。在更高温度的环境中,材料不仅性能指标更差,性能的分散度也会增加,可靠性会大幅降低,所以在进行结构设计时需要尽量保证结构在工作过程中的温度处于材料的推荐使用温度之内。而基于传统的一种材料的承载结构设计方案,为降低工作过程中结构的温度就必须在结构中加入更多的TA15或使用耐温性更好而密度也更大的高强度材料,而这2种方案往往都会造成结构的轻量化要求难以满足。铝基相变材料具有密度小,储热密度大,导热率高等优点,可以高效地提高结构热沉,延缓结构的温升速率,提高加热状态下结构的承载能力。表2中给出了5种目前研究较多的铝基相变材料和TA15的热物性能参数。6种材料在0~1 000 ℃范围内的单位质量储热量曲线如图3所示。

表2 铝基共晶合金与TA15的热物性参数[4,16]Table 2 Thermal physics properties of Al-based eutectic alloys and TA15[4,16]

图3 铝基相变材料与TA15的单位质量储热量曲线Fig.3 Curve of unit mass heat storage of aluminum based phase change material and TA15
可以看出,Al-35Mg材料由于其比热容较高,在整个温度区间内单位质量储热量一直都处于很高的水平,而Al-Si-Mg虽然比热容不及Al-35Mg,但其凭借更高的相变潜热,在整个温度区间的后半段达到了与Al-35Mg相近的储热量水平,不过两者的相变温度、相变潜热以及导热系数均有较大差异,两者的降温效果需要根据其各自的优化构型进行比较。
所以,本文基于Al-35Mg与Al-Si-Mg 2种铝基相变材料,利用第1章中介绍的KG-MFSE拓扑优化方法,以提高热载荷作用下截面的抗弯刚度为目标,进行由TA15与铝基相变材料构成的加强筋截面的拓扑优化设计。
2.2 有限元模型与设计域说明
加强筋1/4截面的有限元模型如图4 所示,为一个12 mm×6 mm的矩形平面离散为48×24的平面有限元模型。整个矩形平面分为3个区域,分别是设计区域、非设计区域和孔洞区域。非设计区域的材料为TA15,它的设置是为了保证加强筋纵向传力路径的连贯性以及对设计区域中会熔化为液体的相变材料的包裹性。此外,由于铝基相变材料的密度小于TA15合金,在质量约束的作用下,加入铝基相变材料的加强筋截面面积可能会有所增大,所以本文在进行加强筋截面拓扑优化的同时也将加强筋的凸缘厚度L作为设计变量进行了优化设计。当L的取值发生变化时,设计域形状也会发生变化,而非设计区域的厚度保持不变,如图4所示。由于设计域在优化过程中是不断变化的,如果只建立设

图4 优化设计域设置Fig.4 Design area of optimization
计域的材料场函数按1.1节当中的方法进行拓扑描述实现起来会比较繁琐。所以,在图4所示的整个矩形区域中建立了材料场函数。在建立有限元模型时,首先判断单元所属区域(孔洞、非设计区域或设计区域),若单元处于孔洞区域或非设计区域,则直接赋予单元孔洞或TA15的材料属性;若单元位于设计域中,则根据单元中心点处材料场函数的值,按照式(7)~(11)赋予单元相应的材料属性参数。
此外,为模拟加强筋结构在工作过程中的温度场变化,在加强筋的上表面施加54.6 kW/m2的恒定热流密度,作用时间为300 s,其余边界绝热。
2.3 优化目标与优化问题模型
以截面的抗弯刚度Dx作为优化的目标,由式(18)可知,截面抗弯刚度的计算需要不同温度下TA15的弹性模量数据(考虑到复杂异质材料构件的成型工艺限制,文中暂不考虑相变材料在结构中的承力作用)。但如表1所示,目前可查的不同温度下TA15弹性模量的数据最高只给到550 ℃,而优化过程中会出现结构最高温度远高于550 ℃的样本,由于缺乏更高温度下弹性模量的数据,这些样本的截面抗弯刚度难以计算。但从优化的角度分析,由于希望优化结果的整体温度处于TA15的使用温度之内,所以结构中最高温度高出550 ℃越多的样本,其目标函数值应当越差。因此,可以通过对TA15更高温度下弹性模量的惩罚,使截面温度过高的构型的目标函数值更小,从而实现对高温构型的目标函数值的惩罚,避免得到截面最高温度远高于TA15使用温度极限的优化结果。经试验,基于图5所示的弹性模量随温度的变化曲线可以在保证优化过程收敛性的同时获得满足使用温度要求的优化结果。

图5 TA15弹性模量随温度变化曲线Fig.5 TA15 elastic modulus versus temperature curve
所以,根据图5所示的E(T),以热载荷作用300 s时刻截面的抗弯刚度最大作为优化目标,优化问题的数学模型可定义为

式中:C为等效热容阵[8];K为等效热传导阵;P为施加的热载荷向量;m0为质量约束值。
2.4 优化流程
基于第1章中所介绍的KG-MFSEf拓扑优化方法进行考虑相变过程的含相变材料截面拓扑优化设计的流程框图,如图6所示。
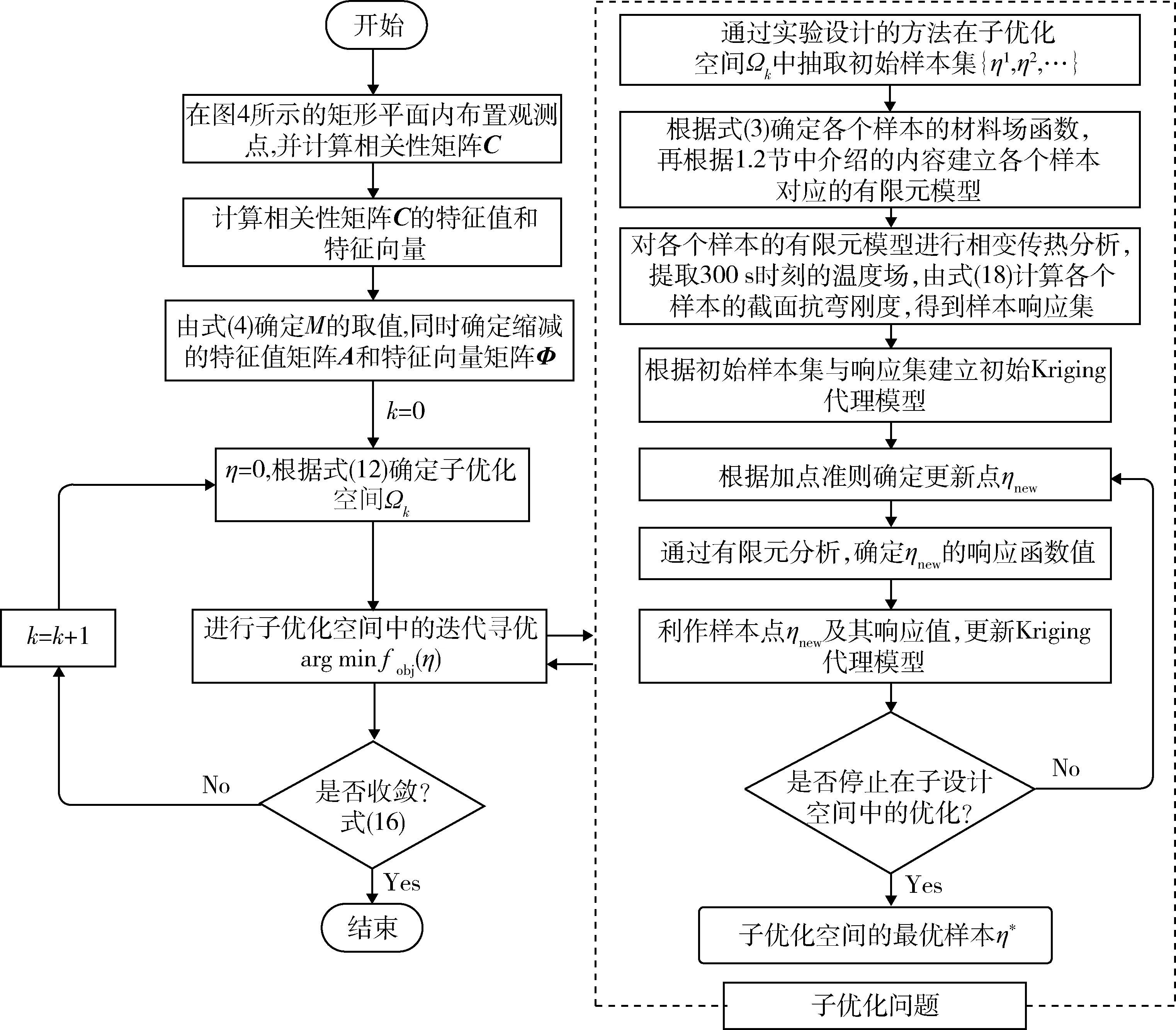
图6 基于KG-MFSE方法的优化流程框图Fig.6 Optimization flow chart based on KG-MFSE method
2.5 优化结果与讨论
以原始设计的截面质量为约束,以300 s时刻的截面抗弯刚度最大为优化目标,进行了加强筋截面的拓扑优化,图7为在截面中加入Al-35Mg时的优化收敛过程,经过不到1 200次的有限元计算后实现了收敛。

图7 优化设计2的拓扑优化过程Fig.7 Topology optimization process of the second optimization design scheme
表3对3种设计方案进行了对比,在截面质量相同的约束下,优化设计1,2中分别加入了 14.92% 的Al-Si-Mg和19.2%的Al-35Mg,与原始设计相比,300 s时刻的截面最高温度分别下降了244 ℃和298 ℃,降温效果十分明显,得益于截面整体温度的大幅度下降,优化设计1,2于300 s时刻的截面抗弯刚度与原始设计在200 s时刻的截面抗弯刚度几乎持平,仅下降了不到5%。图8中为3种设计方案的材料分布和300 s时刻的温度场分布。

图8 3种设计方案的材料分布及300 s时刻的温度场Fig.8 Material distribution of three designs and temperature field at 300 s

表3 3种截面构型的性能对比Table 3 Performance comparison of three cross section configurations
图9为3种截面最高温度随时间变化的曲线,可以发现,相变材料的加入使截面的升温曲线出现了明显的平台期,含Al-35Mg截面的最高温度升温曲线的平台期开始于233 s,在278 s处结束,持续时间45 s,期间,最高温度由466.4 ℃增长到484 ℃,仅增长了17.6 ℃;含Al-Si-Mg截面的最高温度升温曲线的平台期开始于244 s,一直持续到热载荷作用结束,持续时间≥56 s,最高温度由572.7 ℃增长到593 ℃,增长了21.3 ℃。

图9 3种设计方案的最高温度温升曲线Fig.9 Maximum temperature rise curves of three design schemes
此外,在200~300 s这段时间内,随着热载荷作用时间的增加,原始设计的温度方差由23 347.4上升到了37 650.9,而优化设计1,2中由于相变过程的发生,温度方差不升反降,分别由15 073.8和10 364.9 降低到了11 137.6与8 810.9,体现了相变过程对于提高结构局部温度场分布均匀性的显著作用。
可以发现,加入Al-35Mg的方案获得了更好的降温效果,分析认为,这主要是由于Al-35Mg材料的相变温度更低,在工作温度区间内总储热密度更大(显热+潜热),具有更高的降温效率,所以在优化结果中加入Al-35Mg的比例更高,结构的热沉也更大,降温效果也更加显著。而Al-Si-Mg材料凭借更大的单位质量相变潜热,在含量少于Al-35Mg的情况下依然为结构带来了更长时间的平台期。
综上所述,相变材料的加入对于降低局部结构温度、提高局部温度分布均匀性有着显著的效果,而且凭借相变材料可观的相变潜热,可以较长时间的使结构局部温度维持在相变材料的相变点附近。
3 结束语
本文针对工作于高温环境中结构的热适应或热防护问题,提出了一种基于相变材料的新型热控思路。以在热载荷作用下承受弯曲载荷的加强筋的截面为研究对象,通过考虑材料的温度效应以及对更高温度下弹性模量的惩罚,构建了截面的热弯曲刚度拓扑优化模型,基于KG-MFSE非梯度拓扑优化方法进行了含相变材料加强筋截面的拓扑优化,经过不到1200次的有限元计算之后实现了收敛,得到了基于Al-35Mg和Al-Si-Mg两种铝基相变材料的优化截面构型,对优化构型的分析表明,在TA15加强筋截面中加入铝基相变材料可以高效的延长加强筋结构在高温环境中的工作时间。

