临近空间目标跟踪与预报技术研究 *

李君龙，周荻，王冠，陈晓波，秦雷

(1．北京电子工程总体研究所，北京 100854；2．哈尔滨工业大学， 黑龙江 哈尔滨 150001；3．中国航天科工集团有限公司 第二研究院，北京 100854)

0 引言

2001年，美国国防部提出“新三位一体”战略，加快了临近空间进攻武器的发展步伐。2010年，《四年防务评估报告》将“在反介入环境下威慑和击败进犯”列入美国国防六大优先任务；2012年，《新军事战略方针》将“反介入区域拒止环境军力投送”列为十大优先任务之一。临近空间高超声速打击武器在美国新一代攻击体系中占有重要地位。在高超声速巡航导弹方面，美国空军X-51A已完成4次飞行试验，武器化原型“高超声速吸气式武器概念”(hypersonic air-breatking weapon concepi,HAWC)项目预期射程1 100～2 200 km，将重点用于对时敏或强防护目标的远程快速打击。俄印正联合开展“布拉莫斯-Ⅱ”高超声速导弹研究[1]，印度完成了高超声速技术验证飞行器(hypersonic technology demonstrating vehicle,HSTDV)研制及飞行试验。在高速滑翔弹头方面，美国空军“高超声速技术飞行器”(hypersonic technology vehicle,HTV-2)、陆军“先进高超声速武器”(advanced hypersonic weapon,AHW)等均已完成2次飞行试验。HTV-2滑翔距离可达上万千米，从美本土发射可实现全球打击。基于HTV-2技术基础，美军正在开发“战术助推滑翔弹头”(TBG)，射程可达1 800 km，用于实施战区快速打击任务。AHW射程最远达7 800 km，主要依靠海外基地多点部署实现全球覆盖，技术成熟度高，并正开展潜射改进型研制。此外，常规弹道导弹也在发展超低离心弹道、再入机动弹道等突防样式，经由临近空间实施打击。临近空间飞行器主要具有如下特点：

(1) 飞行速度快，攻击范围广。临近空间飞行器借助稀薄大气进行机动，飞行Ma可以高达20，在20～100 km的临近空间可长时间飞行，最长飞行时间可超过3 000 s，横向机动距离可达射程的1/3，洲际打击可超5 000 km。

(2) 机动样式多样多变。临近空间飞行器的轨迹一般包括助推段、变轨段、滑翔段和下压段。其中滑翔段高低方向可分为跳跃滑翔和平滑滑翔等模式，方位方向分为C型机动和S型机动等模式，此外在打击过程中还可进行突然躲避机动和绕过防区机动。

随着临近空间目标进攻武器的迅猛发展，美国和俄罗斯正发展临近空间防御武器。美发布最新版《导弹防御评估》报告，将“弹道导弹防御”改为“导弹防御”，防御对象从弹道导弹扩大到高超声速导弹。美军以临近空间防御发展为契机，正在构建弹道导弹防御、巡航导弹防御、滑翔弹头防御为一体的防御体系。大力发展天基能力层(hypersonic and ballistic tracking space sensor,HBTSS)，对发射平台进行监视、对发射后的临近空间飞行器进行跟踪。随着临近空间高超声速打击武器的发展，俄罗斯意识到“常规快速全球打击武器的威胁已经接近战略核武器水平”，并提出要在外军临近空间武器部署前形成防御能力。俄罗斯航空航天部队总司令接受采访时透露，C-500系统能够打击所有改进型高超声速飞行器。临近空间目标跟踪与预报对临近空间目标防御具有重要的意义。由于临近空间目标非弹道式机动飞行，机动模式多变，因而临近空间目标跟踪与预报面临重大技术挑战。

1 临近空间目标目标跟踪与预报发展现状

临近空间目标跟踪与预报是新的研究方向，目前正处于探索与概念研究阶段，存在许多基础科学问题。

在目标探测方面，针对弹道导弹和常规气动力目标，形成了卫星、雷达等多传感器测量与误差建模方法。临近空间机动目标探测和常规目标探测有很大不同：目标的强机动会引起目标运动轨迹和姿态大动态变化，引入新的误差项，如目标姿态变化引起的散射中心变化与RCS(radar cross-sectior)起伏、时变等离子鞘套对雷达探测有较大影响，对其测量误差的影响规律与建模等尚缺乏系统研究[2-5]。

在误差模型构建方面，针对强机动目标伴随的非高斯时变噪声问题，有学者提出了基于时变AR模型的非平稳非高斯随机过程的模拟方法。然而，临近空间机动目标跟踪系统中量测噪声是多物理场环境、等离子鞘效应和传感器自身探测的强耦合作用的结果，将呈现出十分复杂的强耦合非线性快时变特性，目前尚未开展深入研究，因此亟待开展相应的基础理论研究。

在非线性滤波方面，传统UKF方法多用于具有强非线性的导弹再入跟踪问题，但要求系统噪声和量测噪声服从均值为0的高斯分布。针对噪声非高斯分布问题，有学者提出了基于统计回归估计的鲁棒CKF(cubature Kalman filter)算法,但仅限于解决特定噪声问题，不适合处理临近空间机动目标跟踪中强耦合非线性快时变噪声的情况。因此有必要对非高斯非线性的滤波算法进行进一步研究，以解决临近空间飞行器跟踪中的强耦合非线性快时变噪声数据融合问题。

在多模型算法方面，目前主要有静态多模型算法、交互式多模型算法和变结构多模型算法。静态多模型算法适用于目标运动模型保持不变的情况；交互式多模型算法应用于机动目标跟踪，但模型集中的模型间存在交互与跳变；变结构多模型算法，根据先验信息预先设定一个密切相关的模型集群以及自适应切换逻辑，相比交互式多模型算法提高了跟踪精度。然而，现有的算法存在着模型切换易出错、模型集调整速度慢和对初始模型集过于依赖等问题，难以满足强机动目标高精度探测跟踪需求。因此，有必要提出一种新的变结构多模型算法以解决现有算法存在的问题。

在机动突防模式及攻击意图研究方面，目前机动突防的研究主要集中在弹道导弹和飞机等常规目标方面。对临近空间高超声速飞行器的相关研究刚刚起步。通过博弈的角度，根据目标的运动轨迹约束、防御阵地的部署、核心打击节点等判断目标的攻击意图尚处概念研究阶段，由于临近空间目标的种类各式各样，目标信息的获取和判断具有不确定性，后续需要将计算机辅助决策和人工智能等方法逐步运用到临近空间目标打击意图识别中。

在目标轨迹预估算法研究方面，针对弹道导弹目标，通过弹道导弹关机点的速度和位置，可对飞行轨迹预测，由于目标非机动，可比较准确地预测目标运动轨迹。目前，针对临近空间机动目标，受目标机动水平和模式的影响，运动轨迹变化范围较大，呈管道型包络，尚未有成熟的飞行管道预测的相关理论与方法。针对弹道导弹，出现了很多高精度算法，如基于距离信息修正的自由段弹道预报法、基于距离修正的分段弹道预报法等，提高了观测数据的利用率和弹道预报的精度。针对临近空间高超声速目标轨迹预测，国内外目前尚处于理论探索阶段。虽然弹道导弹轨道预报技术相对成熟，但其对临近空间机动目标的预估可借鉴性和可移植性较差，且未考虑弱观测条件，难以对长时间尺度的飞行轨迹进行高精度预测。

2 临近空间高超声速飞行器的运动特性

2.1 临近空间高超声速飞行器运动模型

对高超声速滑翔弹头的拦截主要发生在滑翔飞行段，相应雷达对滑翔弹头的探测跟踪与轨迹预报也主要在滑翔飞行段，因此本文重点关注滑翔弹头的滑翔段弹道及其运动特性。

在半速度坐标系下，考虑地球引力和地球自转，建立高超声速滑翔弹头(以下简称滑翔弹头)在气动力和地球引力作用下的动力学模型，如式(1)所示。滑翔弹头位置矢量表示为(r,λ,φ)，r为地心径长，λ为地心经度，φ为地心纬度;速度矢量表示为(v,θ,ξ)，v为速度大小，θ为当地速度倾角，ξ为速度方位角。

高超声速巡航导弹和滑翔弹头在半速度坐标系下模型如下：

(1)

高超声速滑翔弹头绝大部分时间飞行在滑翔段，依靠较高的升阻比，进行无动力滑翔飞行，并可利用气动力进行纵、侧向机动。在纵向平面内，可采取平衡滑翔或跳跃滑翔机动模式，在侧向平面内，可采取侧向S型机动等弹道形式。

2.2 平衡滑翔弹道

(2)

升力加速度aL主要受攻角和马赫数影响。滑翔弹头实际飞行时，制导控制系统根据式(2)控制滑翔飞行器的升力，即可实现平衡滑翔运动。从图1可看出，在准平衡滑翔过程中，高低方向加速度ay≈0。

图1 典型平衡滑翔弹道曲线Fig.1 Typical equilibrium glide trajectory curve

2.3 跳跃滑翔弹道机动

跳跃弹道是指飞行器再入大气层后，不直接俯冲打击目标，而是在进入低空后重新拉起，依靠升力作用实现无动力爬升，形成多个“抛物线”弹道，可增大射程，增加拦截难度，增强突防性能。

(1) 攻角线性调度方案

跳跃滑翔弹道的攻角通常可采用线性调度策略。典型攻角剖面如图2所示，攻角按飞行速度进行调度，当速度较大时，采用最大攻角飞行；当速度较低时，采用最优升阻比攻角飞行；当速度在一定范围内，则采用线性函数进行调度。图3为攻角采用线性调度策略的跳跃滑翔弹道曲线。

图2 跳跃滑翔弹道攻角剖面曲线Fig.2 Angle of attack profile curve of jumping glide trajectory

(2) 等攻角方案

与攻角线性调度方案不同，等攻角方案全程采用固定攻角。滑翔弹头在实际飞行时，制导控制系统根据等攻角调度策略，可实现侧向无机动的跳跃滑翔弹道。滑翔弹头在进入低空后重新拉起，依靠升力作用。实现无动力爬升，形成多个“抛物线”弹道，可增大射程，增加拦截难度，增强突防性能。

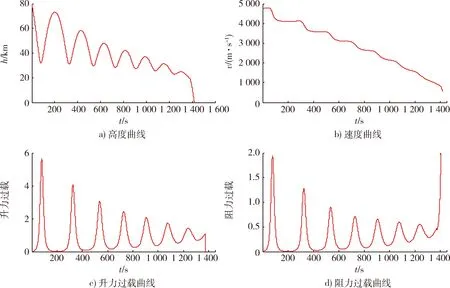
图3 跳跃滑翔弹道曲线Fig.3 Trajectory curve of jump glide

2.4 侧向S型机动模式

为快速实施对目标的打击，滑翔弹头在高低方向通常采用平衡滑翔弹道机动模式，跳跃滑翔弹道机动模式。但当滑翔弹头在打击目标路径上遭遇防御方的防御阵地时，为增强突防能力，滑翔弹头在侧向可实施机动以绕过防御阵地，如侧向S型机动、侧向C型机动，其中C型机动可看成是S型机动的特例。

典型S型机动可见式(3)表示

z(t)=lzsin(ωzt+η0),

(3)

式中：z为滑翔弹头运动的侧向距离；lz为机动幅度；ωz为机动角速度；η0表示相位。

为实现S型机动，滑翔弹头的制导控制系统需同时控制攻角α和倾侧角σ。攻角仍可采用线性调度策略方案或等攻角调度策略方案。

综上所述，滑翔弹头可通过控制攻角和倾侧角来实现高低和方位方向弹道机动，而高低和方位方向又有多种机动模式，这就使得弹道机动模式多样化。

3 临近目标导弹跟踪滤波

3.1 机动模型

由于临近空间非弹道式飞行器的机动飞行模式多变，因此对其精确建模具有很大的挑战性。谈到临近空间非弹道式目标建模问题，还要回忆一下机动目标建模的发展历程。

1970年Singer提出了著名的Singer模型[6]用于飞行器状态估计，该模型将飞行器加速度的动态环节设定为一个一阶惯性环节附加上一个慢时变的随机游走过程。尽管该模型对目标位置和速度的估计效果出色，但是该模型中加速度的模型较为简单，导致在目标加速度快速改变的情况下状态跟踪滤波器对加速度的估计收敛较慢。此外，还有考虑了目标位置一阶导数为常速的CV(constant velocity)模型，考虑了目标位置二阶导数为常速的CA(constant acceleration)模型[7]，以及考虑了目标位置三阶导数为常速的Jerk模型[8]，这些机动模型在一定意义上涵盖了飞行器的一些飞行状态，它们与Singer模型一样，可以视为机动目标跟踪中的通用模型。对于临近空间滑翔段高超声速飞行器来说，飞行器的机动过载由气动力产生，使得其加速度变化形式多样。上述的通用机动模型难以涵盖临近空间目标所有的机动形式，使得用其设计的滤波器对临近空间目标加速度的估计效果不佳。为了提高对临近空间目标加速度的估计精度，产生了许多临近空间飞行器机动加速度估计方法。例如，考虑到临近空间滑翔式飞行器在纵向平面内具有周期性的跳跃式机动特性，将目标加速度的变化形式用一个正弦函数表示，并通过滤波方式估计该正弦函数的周期[9]；针对跳跃目标具有周期性衰减特性，提出一种自适应衰减震荡模型[10]；针对再入飞行器，将目标升力与阻力引入到模型中对目标状态进行估计[11-12]；引入3个与气动参数相关的状态变量，结合弹道动力学和运动学方程建立临近空间飞行器的非线性机动模型，这种模型较其他模型在一定条件下具有更高的跟踪和预报精度[13]。

在弹道坐标系的3个轴上定义3个表征气动力的状态变量Zx，Zy，Zz:

Zx=-cxS/mt，Zy=cyS/mt，Zz=czS/mt，

(4)

式中：cx，cy，cz为弹道坐标系的3个轴上的空气动力系数；mt为飞行器质量；S为飞行器等效参考面积。

“近年来，在中央及地方的大力推动下，各地乡村旅游获得了长足发展。”周玲强说，一些先进地区涌现了度假、休闲、康养等业态，乡村旅游进入新的发展阶段；一些后发地区，通过发展乡村旅游实现了人居环境改善、生活品质提升，并逐步推动乡村旅游提质升级。

选取状态变量

X=(x，y，z，vx，vy，vz，Zx，Zy，Zz)T,

式中：x,y,z为飞行器在观测惯性坐标系的位置坐标；vx,vy,vz为飞行器的速度。在临近空间滑翔飞行段,假设Zx,Zy,Zz是慢时变量,可得到飞行器在观测惯性系下的9阶运动模型为

(5)

式中：wx，wy，wz为零均值高斯白噪声,

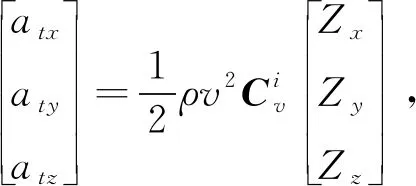
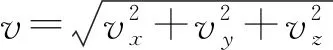
图4 “等攻角调度策略”跳跃滑翔弹道曲线Fig.4 Trajectory curve of jumping glide with equal angle of attack scheduling strategy

观测惯性坐标系Oxiyizi定义如下：取基站所在地O为观测惯性坐标系的原点；xi轴在地心、基站、目标位置三点构成的平面内，与yi轴垂直，指向目标为正；yi轴为地心到基站的连线，指向天为正；zi轴由右手定则得到。弹道坐标系Oxvyvzv定义如下：取飞行器质心O为弹道坐标系的原点；xv轴方向与目标速度方向相同；yv轴在包含速度的铅垂面内，与xv轴垂直，指向上方为正；zv轴由右手定则确定。

根据观测惯性坐标系与弹道坐标系的定义，可以得到

(6)

式中：

将式(6)代入式(5)，可以发现该状态方程是一个复杂的非线性方程

(7)

(8)

当临近空间飞行器作跳跃滑翔或侧向机动时，尤其Zx，Zy，Zz快时变时，Zx，Zy，Zz有各种表达方式。当目标高低方向跳跃或平衡滑翔机动、方位方向S型机动时，Zx，Zy，Zz可表示成式(9)，(10)，在式(9)中的kz变化规律更为简单，式(10)中kz变化规律相对复杂，因包含ψv，θ的影响。

(9)

(10)

将上述非线性方程组与线性位置测量方程结合，即可设计非线性跟踪滤波器。而且，根据上述非线性方程组可以通过数值计算向前一步一步地预报未来的加速度、速度和位置。

当临近空间飞行器在滑翔飞行中作长周期机动的情况下，式(7)关于Zx，Zy，Zz为慢时变量的假设是成立的，该模型有较高的精度。但如果临近空间飞行器利用气动力作短周期的快速机动，该模型则需要进一步改进，改进的方式是引入式(8)，(9)，(10)等模型，使Zx，Zy，Zz能更好地体现目标的机动特征。

3.2 多模型滤波

考虑到目标机动形式的复杂性，机动目标跟踪问题中，采用多模型滤波是一种有效的跟踪滤波方法。例如，为了得到一种对飞行器整个工作状态都有效的状态估计方法，有关文献给出了结合CV模型、CA模型和Jerk模型的多模型状态估计方法[14]。后续发展的多模型状态估计方法[15-17]又增加了常速转弯模型。

跟踪滤波器的结构根据滤波器同时使用的模型数量可以分为单模型滤波器和多模型滤波器。在飞行器的运动模式固定，而且关键运动参数已知或容易估计时，单模型滤波器可以达到很高的跟踪性能。但是在飞行器运动模式不确定或运动模式可能发生跳变时，单模型滤波器往往会因为模型的失配而导致跟踪精度下降甚至估计发散。为了解决这个问题，学者们提出了多模型滤波的概念。多模型滤波是同时采用多个模型并行工作，根据一定的规则将多个模型的跟踪结果融合形成最终的跟踪结果，在跟踪结果融合过程中，和实际模式匹配的模型会获得更高的融合权重。因此，多模型滤波器可以在飞行器运动模式不确定或者运动模式可能发生跳变时依然能获得很好的跟踪性能。

多模型滤波算法经过几十年发展，种类十分丰富。大多数学者都将多模型算法的发展分为三阶段，又称为3代多模型滤波算法。第1代多模型滤波算法于20世纪60年代提出，工作模型集对应的元滤波器完全独立工作，彼此不交互，最终通过估计融合从全部的元滤波器的估计结果得到最终的估计[18]。第1代多模型滤波器适用于飞行器运动模式未知，但是模式不发生改变的问题，能得到比单模型滤波器更好的跟踪效果。第2代多模型滤波器主要解决飞行器运动变化的问题，代表性的多模型滤波算法包括广义贝叶斯算法(generalized peudo-Bayesian,GBP)[19]，以及建立在GPB基础上的交互式多模型(interactive multi-model,IMM)[20]。与第1代多模型滤波器不同，第2代多模型滤波器增加了一个估计混合的过程。经由该过程，所有的元滤波器不再独立工作，每轮滤波周期初始值都依赖于上一周期全部元滤波器的跟踪结果。第2代滤波器可以很好地解决飞行器运动模式变化的问题。多模型需要使用多个元滤波器并行工作。理论上一个使用N个模型的多模型滤波器的计算量大于对应单模型滤波器计算量的N倍。计算量大是多模型滤波器的一个劣势。在一些问题中，需要大量的模型，多模型滤波器的计算量大幅增加，甚至影响多模型滤波器的使用。第3代多模型滤波器主要解决多模型滤波器工作模型集过大的问题。解决的思路比较丰富，但目的是相同的，即通过某种方式动态地调整工作模型集的大小。第3代多模型滤波算法在第2代多模型滤波算法基础上增加了一个模型集自适应的过程。该过程的作用是将匹配当前模式的模型选择进入工作模型集，同时将工作模型集中与当前不再匹配的模型移出。具体算法包括模型群切换算法[21-22]、可能模型集算法[23]、期望模式扩展算法[24]等。

假设系统模型是未知的，或者系统模型因未知而改变。可以使用多个滤波器进行状态估计，并获得更好的状态估计。典型的多模型卡尔曼滤波如下：

(1) 对于j=1，2,…,N，在获得量测值之前，初始每个参数概率,这些概率计为P(pj|y0)。

(2) 在每个时间步长k内执行以下步骤：

2) 在获得k时刻的量测后，每个参数在给定pj的条件下的概率近似值为

式中：

3) 估计p=pj的概率为

在对临近空间目标进行跟踪时，目标的运动模型是未知，其可能的机动模式是多样的，在进行临近空间目标进行跟踪滤波时，采用单一目标运动模型，首先会引起跟踪滤波精度下降，其次难以准确获取目标的运动规律，采用多模型滤波是一种解决目标机动模式未知的跟踪滤波有效方法。临近空间目标跟踪多模型滤波具有多种应用方式，可按(8)～(10)模型进行多模型滤波。

4 临近空间非弹道式机动飞行器轨迹预报

目前，非弹道式飞行器轨迹预测方法研究较多的是数值积分法，在非弹道式目标轨迹预测中不能获取目标先验气动参数模型，同时也不能规划目标攻角、倾侧角等控制量变化模型，需要基于历史跟踪数据与一定的假设条件获取相关模型，进而实现轨迹预测。传统轨迹预测方法直接利用目标跟踪通用模型进行预测，如CA，CV，CT，Singer，Jerk以及当前统计模型等，根据目标当前状态外推后续状态。

从升力过载曲线图1,3可看出，跳跃滑翔弹道的高低方向加速度曲线近似衰减呈振荡形式，平衡滑翔高低方向加速度具有近常值特性。C型或S型具有正弦曲线形式，针对跳跃滑翔弹道，本文对滤波得到的目标加速度信息，进行正弦曲线拟合，从而自动识别出相应的跳跃机动模式。具体如下：

当目标跳跃机动时：ay(t)=eysin(ωyt+ηy)+dy；

当目标准平衡滑翔时：ay(t)=ey+dyt；

当目标C型或S型机动时：az(t)=ezsin(ωzt+ηz)+dz；

当目标跳跃机动时：ax(t)=ex+dxt+fxsin(ωxt+ηx)；

当目标平衡滑翔，无侧向机动时间时：ax(t)=ex+dxt。

针对典型跳跃滑翔弹道，对目标加速度进行跟踪滤波，提取目标加速度信息，对目标加速度进行拟合，获取目标加速度变化规律，根据加速度预示，对弹道进行积分即可获得目标速度、位置的预报。图5，6是针对典型跳跃滑翔弹道的加速度和轨迹预报结果。图7，8是针对典型平衡滑翔弹道的加速度和轨迹预报结果。

图5 典型跳跃滑翔弹道滤波加速度拟合曲线Fig.5 Filter acceleration extraction curve of typical jump glide trajectory

图6 典型跳跃滑翔弹道轨迹预报误差曲线Fig.6 Typical predition error curve of jumping glide trajectory

图7 典型平衡滑翔弹道轨迹预报误差曲线Fig.7 Typical predition error curve of equilibrium glide trajectory

图8 典型平衡滑翔弹道轨迹预报-加速度拟合Fig.8 Typical equilibrium glide trajectory predition-acceleration fitting

取得上述结果的前提是，在预报时段内目标机动模式没有发生变化，否则目前的方法难以保证高精度预报结果。实际上，考虑到拦截系统的需要，预报时间窗口处于临近空间高超声速飞行器在临近空间机动滑翔或巡航飞行弹道的末段，飞行器必须满足落点和落速要求，以及过载、动压等约束条件，在此时间段内飞行器进行机动模式大范围突变的可能性已经很低。当然，从更广泛意义上的非弹道式机动目标轨迹预报的层面考虑，目标机动模式在预测时间段内可能发生变化的情况下，如何挖掘与利用目标潜在信息也成为提高目标轨迹预测精度的一种技术途径。根据挖掘与利用目标潜在信息的方式不同，可将基于目标潜在信息的预测方法分为3类：①利用目标运动机理信息，建立预测模型实现轨迹预测；②采用统计学原理，建立相关控制量的概率分布，实现轨迹预测;③从机动博弈角度，通过引入目标机动意图评估获取目标运动控制量模型。关于第(1)类，即利用目标运动机理信息建立预测模型实现轨迹预报就是我们前面已经阐述过的预报方法。关于第(2)类，即基于概率密度的非弹道式目标轨迹预测方法，一些已有的研究结果可以提供借鉴。在难以获取目标运动状态先验信息的情况下，基于概率密度的预测方法利用统计学理论，通过对目标历史状态信息的分析，获取目标运动轨迹的统计特征，实现对目标的轨迹预测。例如，在实际轨迹预测过程中，结合再入滑翔目跳跃目标运动特征，将运动轨迹分解为具有趋势性、周期性和随机性特征的子序列，并分别针对各项子序列特征选择合适的子轨迹预测模型进行回归预测，最后将各预测结果集成为最终预测结果[25]。再比如，将高超声速再入目标历史轨迹中的控制变量看成混沌时间序列进行轨迹预测，在高维矢量空间中描述目标动力学特性，能够在一定程度上应对目标的无规律机动[26]。还有一些方法是通过建立轨迹密度函数的方法生成轨迹的预报结果[27-29]。采用目标统计学特征对目标的局部状态进行建模，避免了目标运动模式不匹配以及参数估计不准确带来的轨迹预测误差，提高了轨迹预测过程的鲁棒性。但这类方法往往以大量先验信息为样本输入，存在适应目标博弈对抗中准确样本信息难以获取的实际问题，而且轨迹预报的精度难以保证。如果能够获得博弈对抗过程中目标运动的目的性，则可为目标轨迹预测提供更多潜在信息。利用当前状态与预设先验信息之间的关系判断目标机动意图，可以对目标机动模式进行合理推理[30-32]。在实际预测过程中，可通过构造机动意图代价函数进行意图评估，并通过蒙特卡洛采样实现轨迹预测[33]。采用基于动态贝叶斯网络的推理方法对高超声速飞行器与攻击目标之间的攻击关系进行推理，可以预测攻击意图[34]。引入目标潜在目的性信息，可在一定程度上降低预测过程的信息不确定度。但在实际对抗过程中，如何准确提炼目标的这种对抗博弈目的性信息，并将其合理引入轨迹预测过程还有待深入研究。

5 结束语

针对以临近空间高超声速飞行器为代表的非弹道式目标跟踪与预报关键技术问题，根据临近空间目标机动特征，建立临近空间高超声速目标机动模型是提高跟踪与预报精度的有效方法。这种方法对临近空间高超声速飞行器机动模式已知且不变时比较有效。当目标机动模式未知和多变的情况下，采用多模型跟踪滤波方法，有利于提高滤波器对目标多机动模式的适应能力，取得更快的收敛速度和更好的跟踪预报精度。