基于量子状态转移算法的作业车间调度问题
吴贝贝 李 喆
1(新疆大学电气工程学院 新疆 乌鲁木齐 830047) 2(新疆大学网络与信息技术中心 新疆 乌鲁木齐 830046)
Tolerance mechanism
0 引 言
作业车间调度问题(Job-shop Scheduling Problem,JSP)是一类组合最优化问题,其实质就是要解决如何合理地安排工件的加工顺序,将有限的人力物力资源分配给不同的工作任务,使预定的目标最优化的问题。研究该问题,对于在现有的资源条件下提高工作效率和经济效益有十分重要的作用。目前国内外学者已经用多种智能优化算法对JSP问题进行了研究。刘洪铭等[1]提出一种改进粒子群算法,将自适应权重及混沌策略相融合,有效地提升了粒子的利用率,提高了算法的全局和局部搜索能力。孙在省等[2]针对特定的可重入JSP问题,提出一种基于块结构性质的花粉算法用于最小化总加权延误时间,该算法能够在可行解空间区域内进行全局搜索,从而发现较优解所在的区域。张垚等[3]提出了一种新型遗传邻域万有引力算法,并以此定义了一种新的交叉策略,可有效解决某类大规模JSP问题。Dao等[4]提出了一种基于并行式的蝙蝠算法,采用随机键编码方式,以最大完工时间为优化目标求解JSP问题,实验表明该方案可有效提升算法的收敛性及平稳性能。上述优化算法可有效弥补传统算法所存在的不足,并且为求解JSP问题扩展了新的方向。
Zhou等[5]于2012年提出状态转移算法(State transition algorithm,STA),这是一种新型的随机性全局优化方法,因其结构简单、参数少、寻优效率高,得到广泛的应用。王聪等[6]提出了结合正交学习机制和原对偶学习策略的状态转移算法[7]用于分数阶多涡卷混沌系统的辨识。阳春华等[8]提出了一种离散状态转移算法用于求解旅行商问题。王正元等[9]提出了一种基于状态转移算法的组合优化方案,该策略融合了近似方法、下界算法、降维方法及精确求解的方法。董天雪等[10]在一次状态转移的基础上提出了二次状态转移的概念,丰富了解的多样性,使算法跳出局部最优。
量子计算作为突破当前计算极限的重要技术,也成为各国专家学者密切关注的前沿学科之一[11]。量子计算是将量子理论及智能计算二者相融合,并应用量子并行计算特性,能够弥补传统优化算法中的不足,避免算法陷入局部最优,提高算法的收敛速度。对此国内外学者做了大量的研究工作。黄力明等[12]提出了一种新的量子旋转门调整策略,确保当前解无论处于何种状态都能收敛到一个更优的染色体,即最优解染色体。解平等[13]为保证可行解向最优解方向搜索,在量子旋转门更新的基础上同时引入局部更新操作。闫旭等[14]采用量子计算和量子优化的思想提出了一种量子鲸鱼优化算法,可有效解决算法出现的收敛精度低、易早熟的问题。高辉等[15]通过尝试不同的初始旋转角度来进行算例的仿真实验,并探讨分析了初始旋转角对算法性能所产生的影响。Salido等[16]提出了一些分析公式来估计能效、鲁棒性和最大完工时间这些参数之间的比率关系。
本文针对群智能优化算法在求解作业车间调度问题时过分依赖初值、局部搜索能力差、收敛速度慢等不足,提出了量子状态转移算法(Quantum state transition algorithm,QSTA),将量子计算与优化的思想引入状态转移算法构成量子状态转移算法,以最大完工时间最小为目标函数,来求解JSP问题。
1 作业车间调度问题的数学描述
1.1 问题描述
JSP问题一般被描述为:假定有n个工件,它们要经过m台机器加工,每个工件在特定的机器设备上进行加工被称为一道“工序”,每道工序的加工时间是事先确定的。每个工件的加工工艺过程是事先给定的,因此,一个工件可看作一列工序的组成部分。所以调度需处理的问题就是要安排一种合理的工件加工顺序及开始加工的时间,以满足某种性能指标的最优。本文所求解的性能指标为“最小化最大完工时间”,并且在求解该问题时必须满足以下约束条件:
(1) 机器不存在故障,工件从t=0时刻开始加工。
(2) 每台机器在任一时刻最多加工一道工序。
(3) 作业的加工路线必须严格遵守,一旦开始加工不得中途停止,直至这道工序被加工完。
(4) 每个作业的加工工艺固定,不允许改变。
1.2 数学模型建立
求解JSP问题的实质是指在满足上述约束条件的情况下,找到一组可行解(可行的加工工序)并令所要求的目标函数达到最优。实现最小化最大完工时间,可有效提高车间的生产效率,降低企业的生产成本,因此将最大完工时间最小化作为目标函数进行求解具有一定的现实意义。
由于本文求解的决策变量(机器数、工件数)均为正整数,因此利用整数规划模型对JSP问题的数学模型进行描述:
优化目标如下:
(1)
约束条件如下:
Cjk-tik+M(1-aihk)≥Cih
(2)
Cjk-Cik+M(1-xihk)≥tjk
(3)
Cik≥0
(4)
aihk,xijk=0,1
(5)
i,j=1,2,…,nh,k=1,2,…,m
(6)
式中:tik和Cik表示第i个工件在第k台机器上的加工时间以及完工时间;M是一个极大的正数;aihk=1表示机器h比机器k优先加工工件i;xijk=1表示工件i比工件j优先在机器k上加工;反之,二者皆为0。
式(1)为目标函数,表示最大完工时间最小;则式(2)表示当前工序与上道工序之间的约束关系;式(3)表示工序之间是非阻塞约束关系;式(4)表示各工件的完工时间必须大于零;式(5)表示工序、机器约束;式(6)表示各下标变量的取值范围。
2 算法描述
2.1 量子比特位编码
量子计算[17](Quantum computation,QC)首次于1982年提出,现今已成为国内外专家学者所密切关注的前沿问题。进行量子计算时运用量子比特表示信息,采用|0〉与|1〉代替微观粒子所存在的两种基本状态,记号“|〉”称为Dirac记号,在量子力学中表示状态。除了|0〉和|1〉之外,量子比特还可以是叠加态,即这两种状态之间的中间状态:|φ〉=α|0〉+β|1〉,参数α、β代表一对复数,是指量子态的概率幅,即量子态|φ〉以|α2|的概率坍缩到|0〉或以|β2|的概率坍缩到|1〉,且满足:
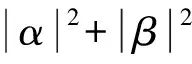
(7)
量子逻辑门是指对量子状态采用逻辑变换所生成的量子装置,它是量子计算可以实现的基础。
2.2 解空间映射方法
解空间映射是将量子比特位编码应用于JSP的关键环节。编码时一定要考虑状态的可行性、有效性和对问题解空间表征的完备性。在求解车间调度问题时,可行解就是工件的排列顺序,所以必须将量子位的概率幅转变成工件的加工工序编码。
在JSP问题中,从一组可行解上进行有限次位置变换生成的解仍然是可行的,本文采用基于移位解码的编码方式和基于实数的交换位编码方式。这两种编码方式均是在一组可行解基础上进行有限次位置交换从而生成新的加工序列,这保证了状态的可行性和有效性,同时两种编码方式对解空间表征的完备性具有互补作用,详细论述如下。
1) 基于移位解码的编码方式是以父代工件的加工工序作为参考模板,根据某一个二进制串进行移位解码从而得到子代工件工序的编码转换方式[18]。定义二进制串中数值0取当前父代序列的第一位值,数值1取当前父代序列的第二位值,以此策略,顺次从父代个体中取出其值组成子代个体,随后将取出的值从父代中删除,方便选取下一位值,其具体说明如图1所示。运用此方法对序列进行重新排序,有助于增加序列的多样性,并提高算法全局搜索的能力。
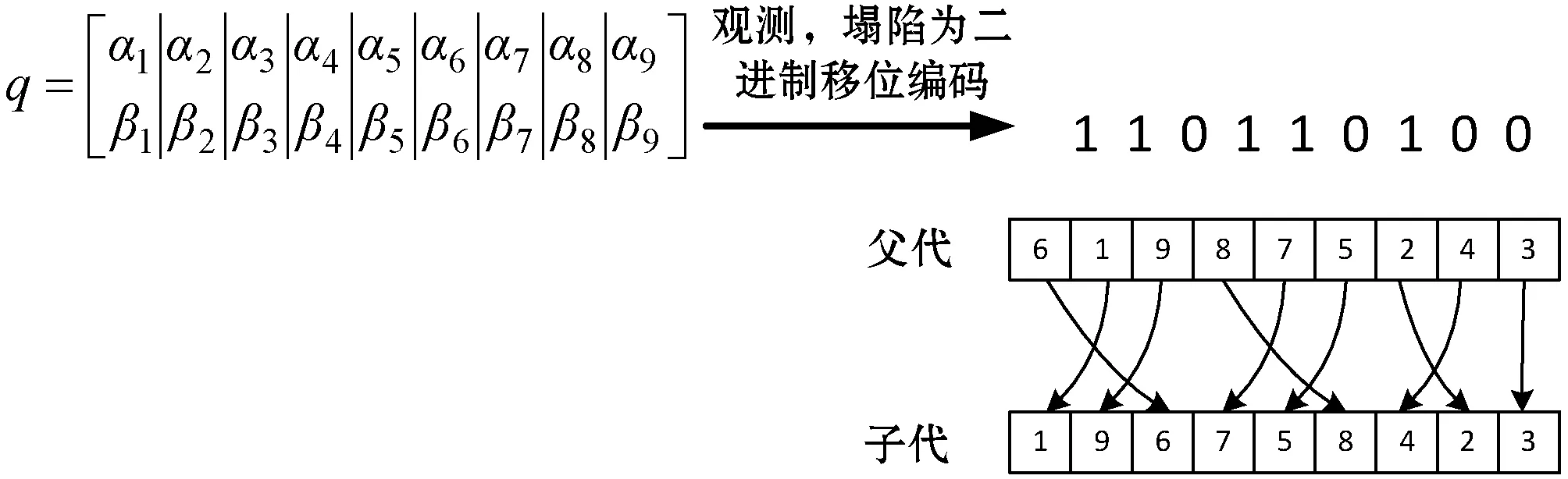
图1 移位解码
2) 为了使加工序列发生微小变化,引起序列更新,本文提出一种基于实数的交换位编码方式。通过交换加工序列中任意两位置的值,从而产生新的加工序列。每一个序列有两个量子串控制其交换位,将量子串转换为二进制数,再换算成十进制编码,进而将加工序列中对应位置的值进行交换。
对于有N个工件M个机器的JSP问题,采用两个最小能表示N×M对应的二进制位数个量子位,一个量子串对应加工序列中的一个待交换位置。例如6个工件6台机器需要6个量子位来描述其工作序列中的位置,量子串被表示为:
(8)
对上述两个量子位串进行观测,如图2所示,若得到二进制串[0 0 1 0 0 0]、[0 1 0 0 1 1],则换算成十进制为[8]、[19],将序列中对应位置的值交换。这种编码方式可以对加工序列进行微调,通过加工序列局部变化引起其序列的更新。

图2 交换位解码
3.3 量子状态转移算法
根据量子的叠加特性及变迁理论,应用量子旋转门变换更新产生新的编码。量子旋转门构造如下:
(9)

(10)

采用状态转移算法作为旋转角搜索策略,同时结合量子旋转门操作提升算法的全局搜索能力。使用状态转移算法中产生候选旋转角的统一框架可以描述如下:
(11)
式中:θk,θk+1∈Rn分别表示旋转角的当前状态与更新后的状态,当前状态对应优化问题的一个解,经过一次算子变换产生的θk+1将构成一个候选解集;Ak,Bk∈Rn×n为状态转移矩阵;uk是关于状态sk及历史状态的一个函数表达式;f(θk+1)表示状态更新后的目标函数值。
为了使QSTA求解问题时量子旋转角状态转移过程具有可控性,依据传统状态转移算法设计了四种量子旋转角状态更新算子。
1) 量子旋转算子:
(12)

2) 量子平移算子:
(13)
式中:β是正常数,称为平移因子;Rt∈R是一个服从[0,1]均匀分布的随机变量。
3) 量子伸缩算子:
θk+1=θk+γReθk
(14)
式中:γ是正常数,称为伸缩因子;Re∈Rn×n是一个服从高斯分布的随机矩阵;该算子主要起到在整个解空间内进行全局搜索的作用。
4) 量子坐标变换算子:
θk+1=θk+δRaθk
(15)
式中:δ是正常数,称为坐标因子;Ra∈Rn×n是一个服从高斯分布的随机对角稀疏矩阵。坐标算子有利于增强单维搜索能力。
对以上四种算子计算出的旋转角分别通过量子旋转门更新量子位,通过量子坍缩操作对量子位进行观测,生成二进制串通过相应的编码方式将其映射到解空间中,可有效增加解的多样性并避免非法解的产生。
2.4 容忍非局部最优解机制
基础的状态转移算法每次迭代过程只考虑当前最优解,在其基础上进行状态转移,然而应用状态转移算法处理JSP问题时容易陷入局部最优,因此本文提出一种对非局部最优解的容忍机制,如图3所示,能够有效避免加工序列处于局部最优状态无法收敛的情况。
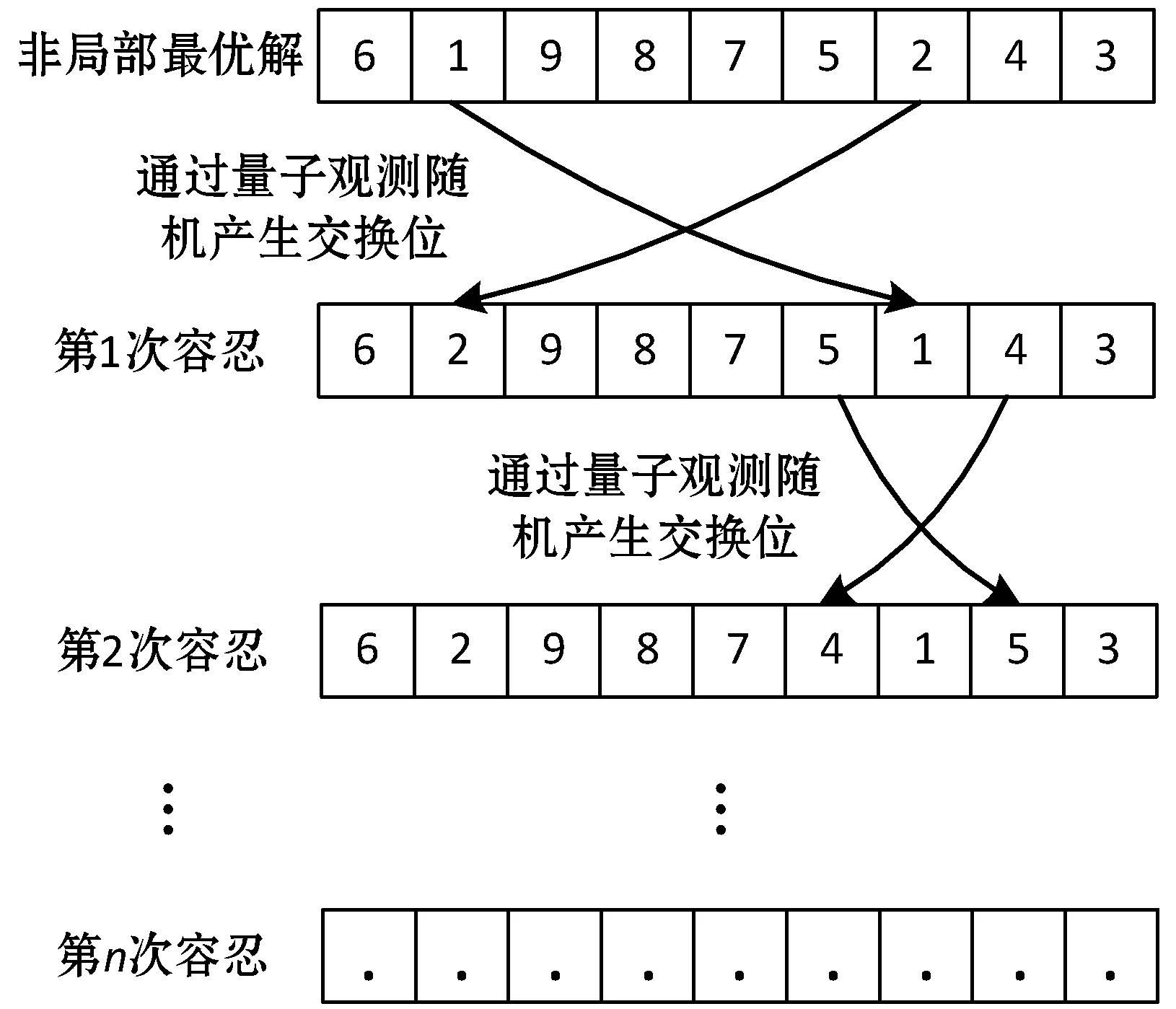
图3 容忍非局部最优解机制
本文考虑单次序列的局部变化,可能不会使新序列获得更好的适应度值,但对同一序列的连续局部变化形成的新序列也有可能导致更好的结果,因此设置非局部最优状态下的容忍次数,允许非局部最优解获得连续的状态变化,以此增加解的多样性,同时有效避免了某一加工序列陷入局部最优。
2.5 QSTA算法流程
量子状态转移算法是在原有状态转移算法(STA)的基础上引入量子旋转门操作以丰富工序的多样性。通过状态转移算法的不同操作更新旋转门所需的旋转角,进行量子旋转门操作。对量子位串观测引起坍缩,生成二进制状态,通过此状态获得不同的加工序列,计算加工工序的总完工时间,进而选出最短完工时间对应的加工序列作为当前最优工序。
QSTA流程如图4所示。
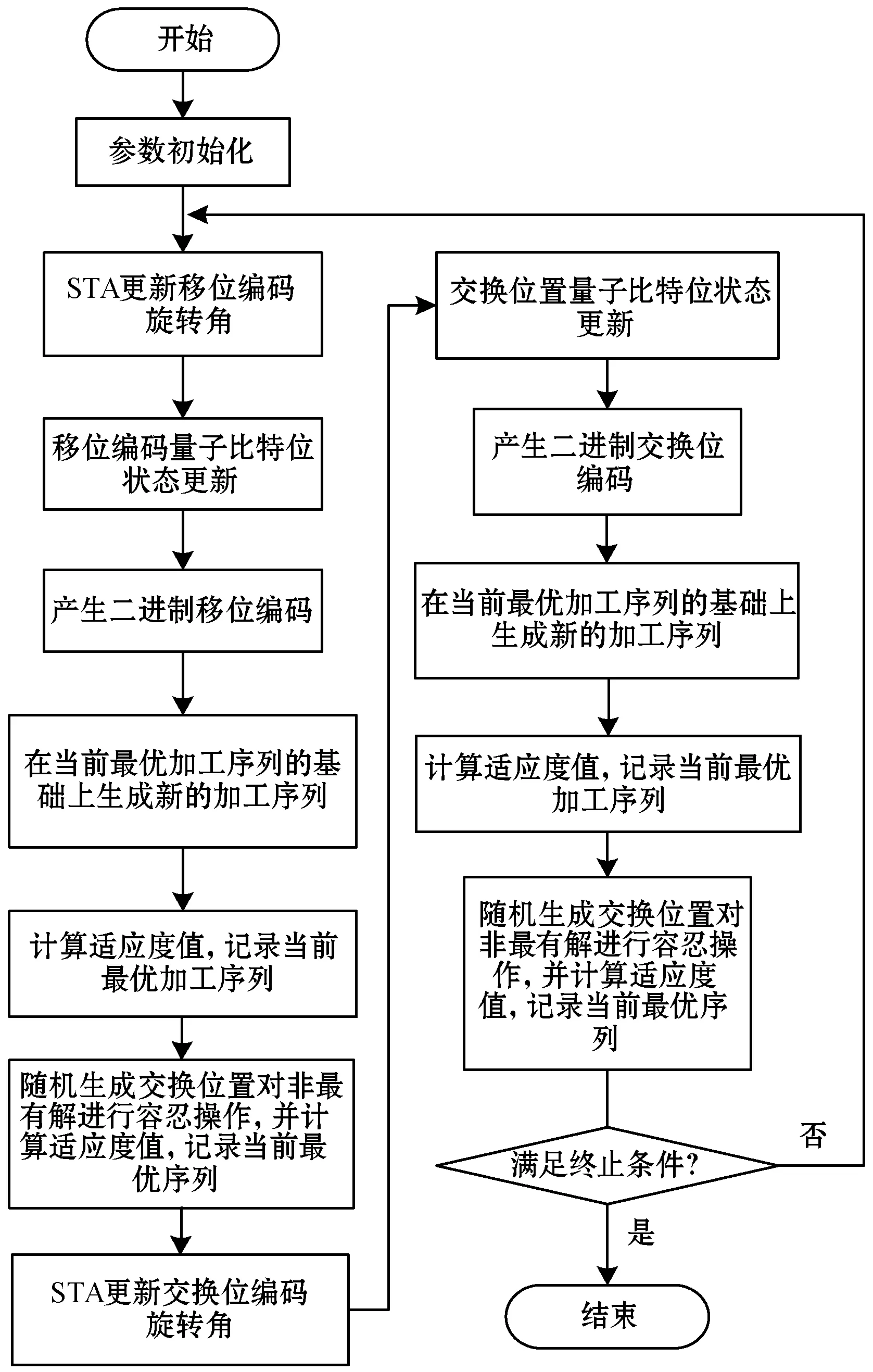
图4 量子状态转移算法流程
QSTA的优化步骤如下:
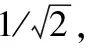
Step2生成二进制移位编码。随机生成移位编码的旋转角,通过量子旋转门对移位编码的量子位串执行量子旋转门操作,对此量子位串进行观测,获得二进制移位编码,使用此编码对全局最优加工序列进行重新排序,然后进行适应度计算,保存最优适应度结果。
Step3对非最优解的容忍操作。对Step 2中所产生的加工序列根据容忍次数连续调整加工序列的不同位置,并对其进行适应度值计算,保存最优适应度结果。
Step4采用量子状态转移算子生成位置交换编码。采用量子旋转、量子伸缩、量子坐标变换操作对旋转角进行更新,通过量子旋转门对交换位编码的量子位串执行量子旋转门操作,对此量子位串对进行观测,获得二进制编码,将其转换成十进制交换位编码,使用此编码对全局最优加工序列中的两个位置进行交换,然后进行适应度计算,保存最优适应度结果。
Step5根据容忍次数连续调整Step 4中所产生的加工序列的不同位置,并对其进行适应度值计算,保存最优适应度结果。
Step6判断是否满足终止条件,若满足则结束搜索,否则返回Step 2。
3 实 验
本实验选用MATLAB R2015b编程语言实现,运行环境为:处理器1.60 GHz,处理器速度1 800 MHz,物理环境3 993 MB,Windows 10操作系统。为验证本文算法解决作业车间调度问题的高效性,采用QSTA方法对作业车间调度标准测试问题库中的12个测试问题进行求解并与其他算法相比较。上述12种算例分别为文献[19]提出的实例FT06、FT10、FT20和Lawrence等[20]提出的实例LA01、LA06、LA11、LA16、LA21、LA26、LA31、LA36、LA40。
3.1 STA、PSO和GA的仿真对比
状态转移算法的参数选择:搜索规模SE=100,旋转因子的最大值αmax=1,最小值为αmin=1e-4,旋转因子α=1,平移因子β=1,伸缩因子γ=1,坐标系数δ=1,迭代次数M=500。为了更准确地与PSO和GA就JSP问题进行比较,将各个参数设置与STA保持一致,即种群规模NIND=100,最大迭代次数M=500。各个算法单独运行20次,所得到的结果如表1所示。

表1 三种算法(STA、GA、PSO)的比较
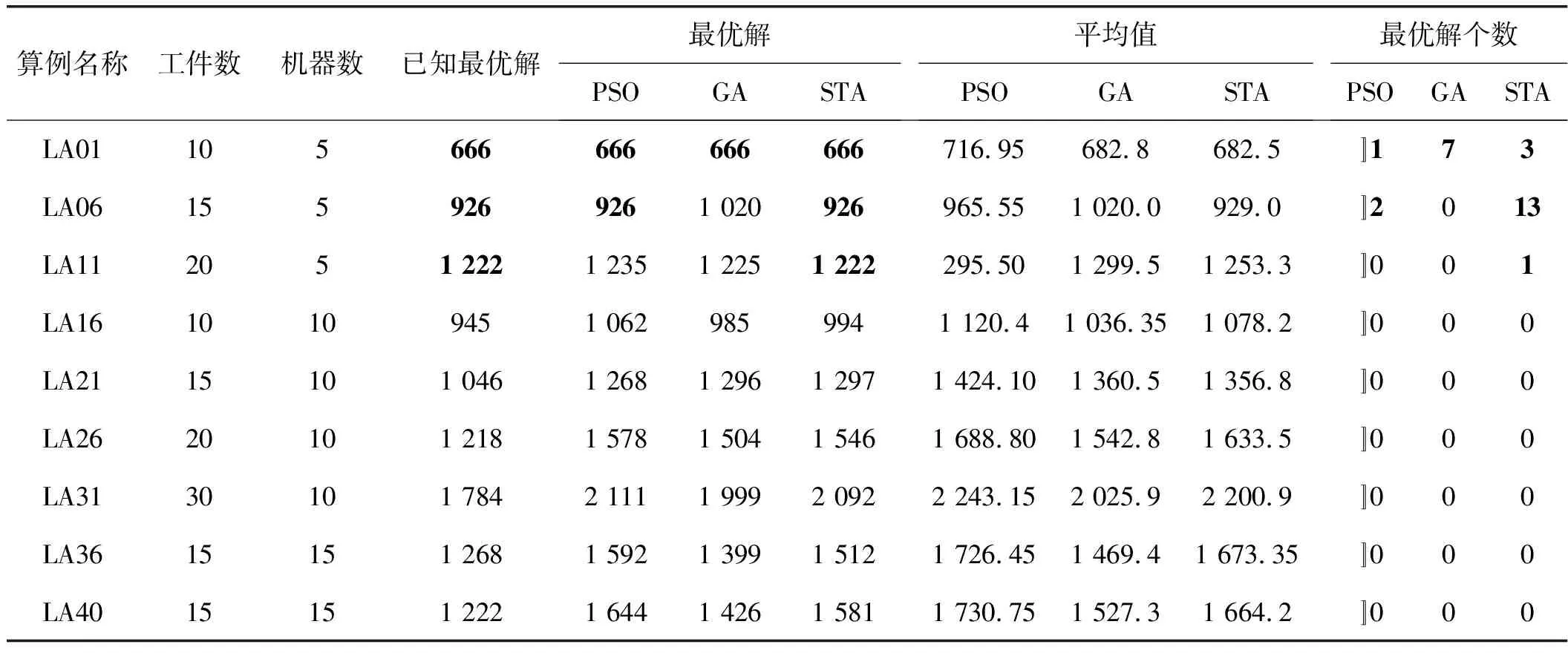
续表1
可以看出,在搜索规模、迭代次数和独立运行次数皆相同的情况下,STA、PSO和GA在FT06、LA01、LA06、LA11等问题中均能收敛到当前已知最优解。在寻最优解个数上STA算法要优于PSO和GA。在计算大规模问题算例时GA要优于STA,从最优解、平均值方面可以得出,STA优于PSO,但部分劣于GA。
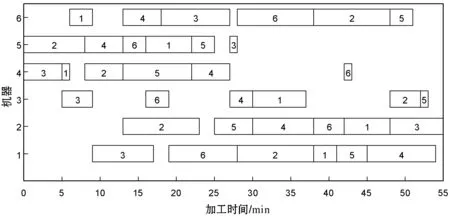
仿真结果表明,STA虽能有效解决JSP,但对比PSO及GA来说并无明显优越性,因此还需对基本STA做进一步的改进,本文采用QSTA继续对以上算例进行求解。QSTA求解的部分甘特图如图5所示。
(a) FT06甘特图(makespan=55/min)
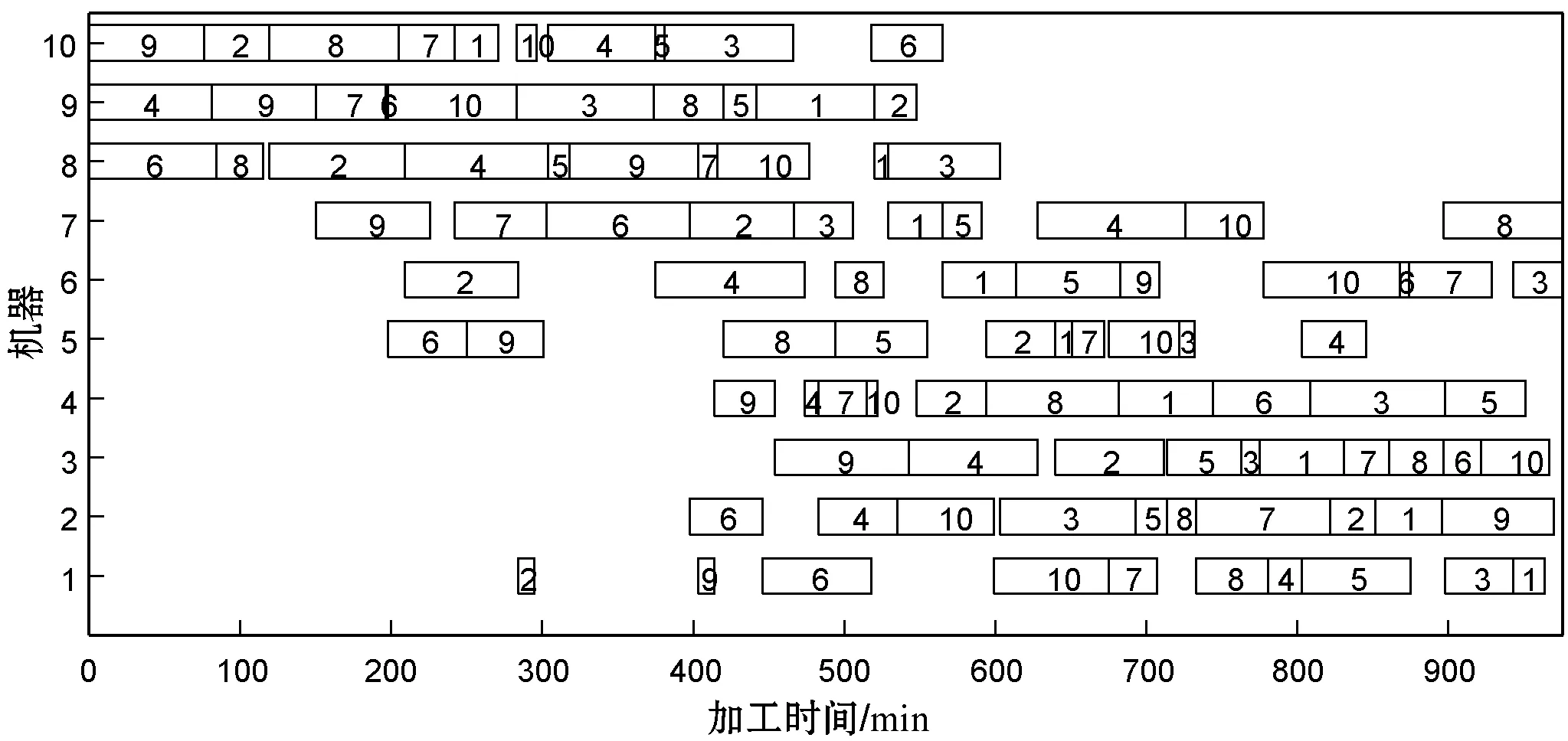
(b) FT10甘特图(makespan=960/min)
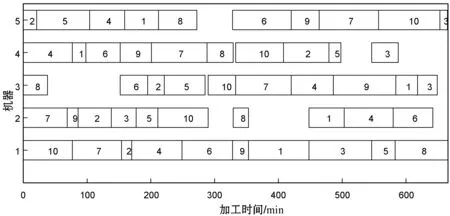
(c) LA01甘特图(makespan=666/min)
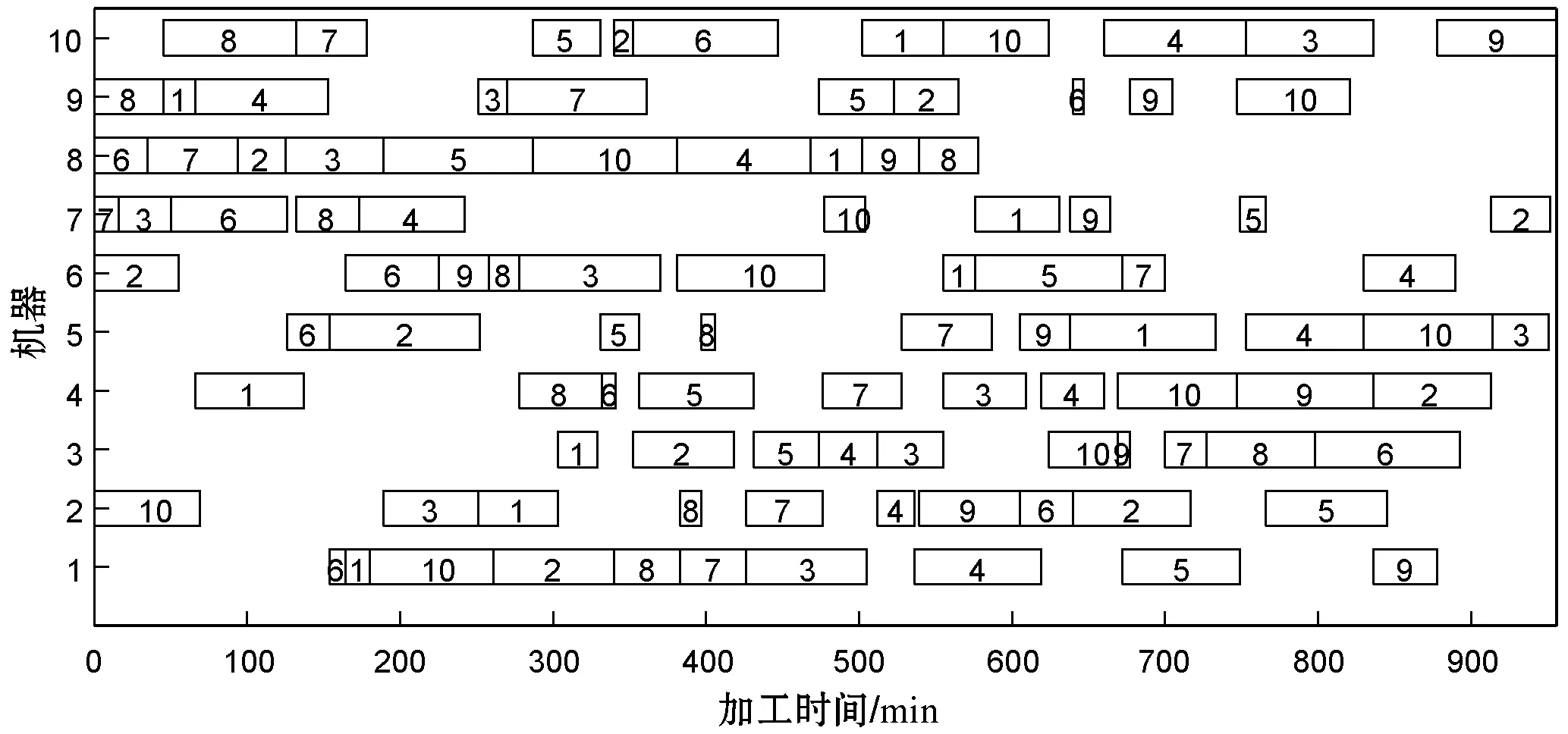
(d) LA16甘特图(makespan=945/min)图5 部分调度问题甘特图
3.2 QSTA与STA的对比
利用量子状态转移算法继续对上述问题进行求解,将算法的搜索规模设置为SE=100,最大迭代次数M=500,独立运行20次,量子旋转角设置为rand×2×π。运算结果如表2所示,寻优成功率的计算方法为:最优解个数/独立运行总次数。
通过QSTA与STA算法就求解作业车间调度问题的比较结果可知,量子状态转移优化算法在算法的寻优成功率方面有很大的提升,在LA06、LA11问题上的寻优成功率的值均在100%,且在LA31中QSTA可以搜索到已知最优解。结合图6所示的寻优曲线对比可知,采用QSTA可有效解决JSP问题,QSTA搜索得到的最优解及平均值皆明显优于STA,且收敛速度及收敛精度也明显优于STA、PSO和GA。综上所述,QSTA可有效求解JSP问题,与STA相比其收敛精度更高、收敛速度更快。因此,改进后的量子状态转移算法可有效避免算法陷入早熟,增强算法的求解精度并提高算法的收敛速度。
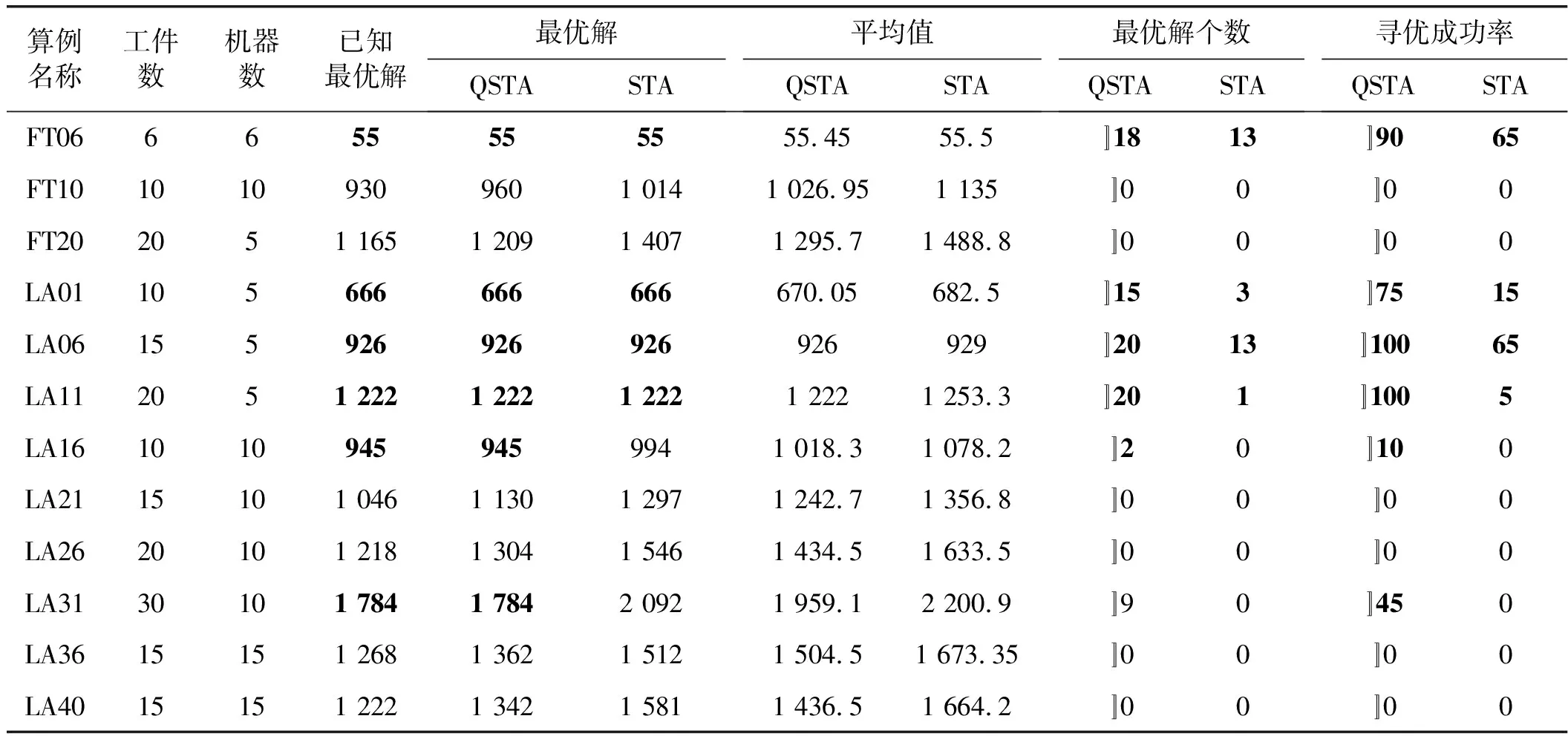
表2 QSTA与STA算法的比较
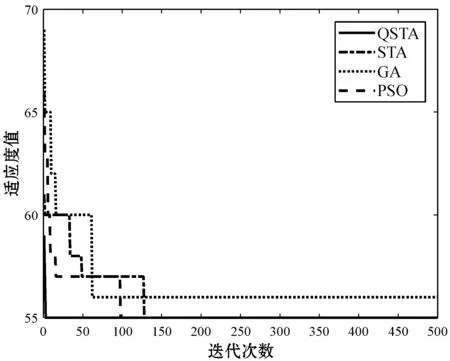
(a) FT06收敛曲线

(b) FT10收敛曲线
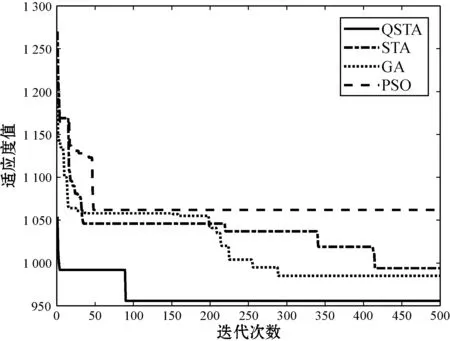
(c) LA16收敛曲线
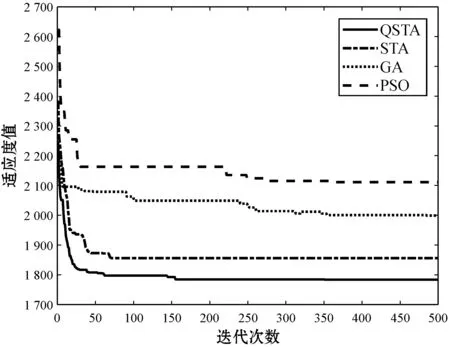
(d) LA31收敛曲线图6 部分测试问题寻优曲线对比
4 结 语
本文针对传统群智能算法求解JSP时存在的算法易早熟、后期收敛速度慢和全局搜索能力差的问题,提出了量子状态转移算法来求解JSP问题。首先,验证了STA在解决JSP时具有可行性,并发现了STA在解决JSP时存在缺陷;为提升STA搜索可行解的多样性及收敛精度,采用移位解码和交换位编码两种编码方式,结合量子计算的优点提出QSTA;在此基础上又提出一种容忍非最优解机制,对其进行仿真实验。通过对比发现,QSTA在解决JSP时可有效弥补传统算法的不足,具有迭代次数少、收敛速度快、全局搜索能力强等优点。

