基于电荷等效法的电容短路放电微观特性数值模拟研究

王党树 栾哲哲 古东明 刘树林 王新霞

（1. 西安科技大学电气与控制工程学院 西安 710075 2. 西安科技大学理学院 西安 710075）

0 引言

容性电路短路时经常会产生火花放电，并且放电时间短、放电能量密度高度集中，很容易引燃周围危险气体，造成人员财产伤亡。基于此，国标GB 3836.4给出最小点燃电压曲线和IEC安全火花试验装置两种方法用来检测爆炸性环境中的容性电路本质安全性[1]。围绕着容性电路爆炸性和非爆炸性本质安全判断，国内外学者进行了大量相关研究。目前主要围绕建模研究，如截止型输出短路保护下容性等效电路模型[2]，基于放电机制的场致发射建立比较理想数学模型[3-4]，基于放电特性曲线分段模型[5]。在这些数学模型下即可得出电容短路放电的最小点燃电压曲线，并进行数值拟合[6-8]，以及对放电引燃特性进行分析[9-10]，数学建模分析只是对放电特性进行宏观描述，无法解释电容短路放电的微观机理。文献[11]是基于电容火花放电，对氢气-空气混合物的最小点火能量（Minimum Ignition Energy, MIE）进行测量，研究发现，在室温下相对湿度从0增加到90%时，火花持续时间从5ns变化到1ms，这表明湿度和火花持续时间对MIE几乎没有影响。也有对电感、电容组成复合电路放电特性进行探讨[12]，针对IEC火花试验装置电容短路放电打火间隔及灵敏度进行分析[13]，以及对两电极等离子体合成射流激励器工作特性研究等[14]。文献[15]提出截止型电容（Electric Potential and Capacitor, EC）电路模型作为研究对象建立了EC电路等效火花放电模型电路，推导出相应的数学模型，并认为电源也参与了放电，这一问题值得商榷。文献[16]认为开关变换器短路输出属于容性电路，可根据最小点燃曲线设计开关变换器参数，为研究本质安全型开关变换器指明方向。以上研究都是在一定假设条件或者近似处理后，得到一个比较理想化的模型，而放电过程具有一定的复杂性和随机性，因此，仅靠数学模型不能准确地描述放电过程。

文献[17]采用纳秒高压脉冲电源对表面介质阻挡放电的电离传播特性进行分析研究，得到不同位 置处的电流曲线；文献[18]建立模型，获得电压U(t)、电流I(t)和能量、功率、持续时间、电容大小以及点火能力等参数的依赖性；文献[19]则提出了一种有界耦合外部电路元件的算法，并给出了二维静电等离子体模型及求解外部电路的方法；文献[20]通过用杂散电容和气态电容电流减去测得的电流来获得放电电流。以上研究均是从宏观角度对外部电路的电压、电流以及气体的放电特性进行模拟研究，而没有从电荷运动的微观角度对放电机理进行分析。实际上基于IEC安全火花试验装置电容短路放电，属于微间隙低电压的放电，这种放电机制属于场致发射机制[21]，由于放电通道被限制在一个很小空间区域内，阴极所产生的电荷量等于电路外接电容所存储的电荷量与电源所产生的电荷量之和，因此可以采用等效电荷法对电容短路火花放电过程进行数值模拟。基于等效电荷法，学者们也做了相关研究，文献[22]对充满氮气的针-板短间隙外接存有电荷电容外电路的电极进行火花放电实验和数值模拟研究，结果表明火花放电时电流通道收缩，电流快速增长，放电通道是非平衡离子体，并且气体温度相当高；文献[23]基于电荷守恒定律，建立了电场三维计算模型，该模型具有方便考察关键点处电场畸变的优势；文献[24]是利用电荷等效及重新分配的方法对C4F7N/CO2混合气体中尖端缺陷的流注放电过程的变化情况进行仿真研究。以上研究表明，从等效电荷法的角度可以很清楚地对火花放电的微观机理进行解释，但大多是氮气或者空气等环境下，而没有在最危险的瓦斯环境下进行模拟研究。文献[25]通过求解电场分布与电荷累积方程，得出间隙电场变化及流注发展时间和动态电荷累积，建立针对流注起始、发展、结束和电荷累积的模型；文献[26]建立真实金属蒸气分布情况下真空微观粒子动力学模型，求解电子、重粒子输运方程，揭示非均匀分布金属蒸气影响下电弧形成过程。这些研究均表明等效电荷法对极板放电时的电荷状态以及电场分布都有很直观的表示。因此，本文将根据等效电荷法对瓦斯环境下电极击穿后的极间电压、电流曲线及空间电荷的运动情况进行数值模拟研究。

实际上容性电路短路放电特性不但与外电路参数有关，也与试验电极材料性质、电极表面形状、电极间距等参数有关。放电过程是很复杂的物理过程，基于等离子体数值模拟是研究微放电过程和等离子特性必不可少的手段。目前一般采用等离子体流体模型、粒子网格-蒙特卡洛模型（Particle- in-Cell/Monte Carlo Collision, PIC/MCC）或混合模型。文献[27]建立容性耦合射频等离子体放电的一维流体模型，设定He为工作气体，数值模拟研究不同电压、不同气压条件下等离子体电子数密度和电子温度的轴向分布，研究发现平均电子密度随驱动电压与输入功率的增加而增加；文献[28]和文献[29]均建立了自适应粒子管理PIC/MCC仿真模型，充分考虑了电子与气体分子间的弹性碰撞、激发碰撞和电离碰撞过程及其对电子运动产生的影响，研究了低温低压下电容耦合射频在氦气和氩气中的放电，比较适用于在鞘层区域形成的过程。其中流体模型是从宏观的角度去描述等离子体在空间中的放电过程，而粒子网格-蒙特卡洛模型可以从微观角度观察间隙放电时的粒子运动，从而解释放电过程的物理机理。因此本文将采用PIC/MCC模型对火花实验装置两电极介质击穿后也就是电容输出短路后火花放电过程中各种粒子微观特性进行研究。

为了探究容性放电的物理机理，本文采用等效电荷法，建立二维PIC/MCC模型，对电容短路后火花放电的发展进行数值模拟研究。分析了不同的极间电压、极间距及外接电容对火花放电起始和发展过程的影响，同时对平均电子能量，以及气体粒子分布规律进行对比。该模型的建立更加接近放电的实际情况，并且可以直观地观察到火花放电微观参数的变化过程。

1 容性电路短路放电试验电极物理模型

利用IEC安全火花试验装置对容性电路进行短路放电实验，电容短路火花放电的试验电路如图1所示。图1中，Ui为电源电压，G为安全火花试验装置，R0为充电电阻，R为放电回路的总电阻（包括线路上电阻和火花试验装置的内阻），UH和UC分别为电容短路火花放电期间的火花电压和电容电压，由于通常R很小，因此可以近似为：UH=UC。在进行短路放电试验时，充电电阻R0应该取得大一些，使电容短路之后来自电源的电流尽可能地小，同时电阻R0也不能太大，否则在试验过程中电容充电时间过短，从而影响试验结果的准确性。为保证电容能够充分充电。通常R0的取值范围为1～10kΩ。

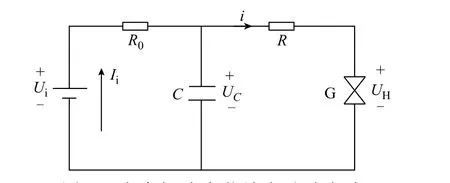
图1 电容短路火花放电试验电路Fig.1 Capacitor short circuit spark discharge test circuit

根据电容短路火花放电试验电路及IEC火花试验装置电极外形，得到实际的IEC火花试验模型，如图2所示。

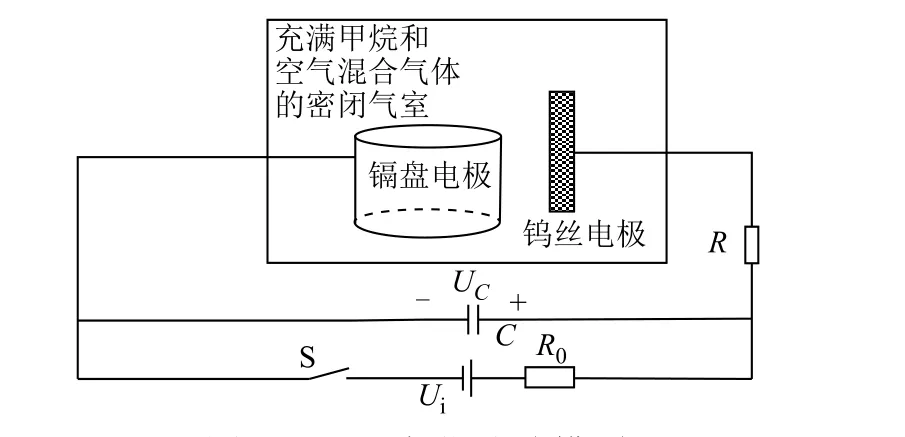
图2 IEC火花试验模型Fig.2 IEC spark test model

2 外电路建模理论

根据电荷守恒定理，放电过程电极上的电荷改变量dQ等于外电路电容C的电荷改变量dQC加上电极收集等离子体对流电荷产生的电荷改变量Qconv，即

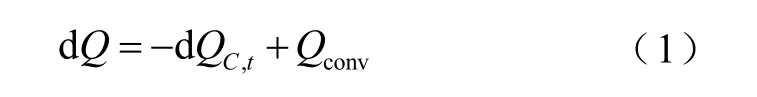
在t时刻展开，此时放电板上存储的电荷为

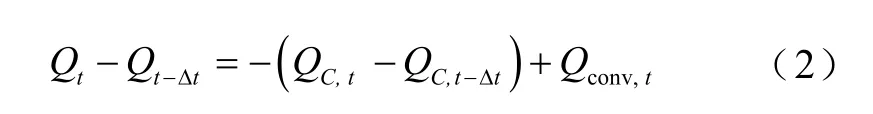
式中，Qt-Δt、QC,t-Δt可根据式（3）和式（4）得到。

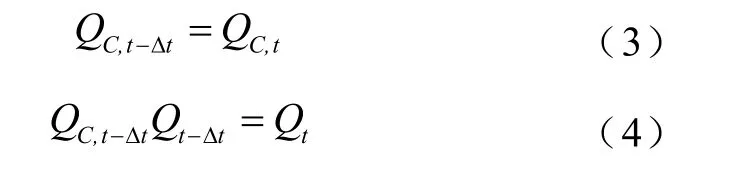
而外电路等效方程是一个关于电流的线性方程，将电荷变化代替电流变化，由戴维南定理可得

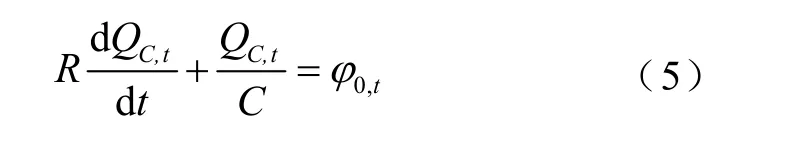
式中，C为外电路实际电容值；φ0,t为电极两端电势，且

式中，CG为平行板电极等效电容

在t时刻对式（5）进行差分展开后得到

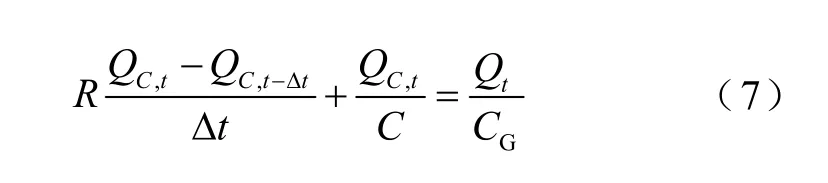
对式（7）进行整理得到

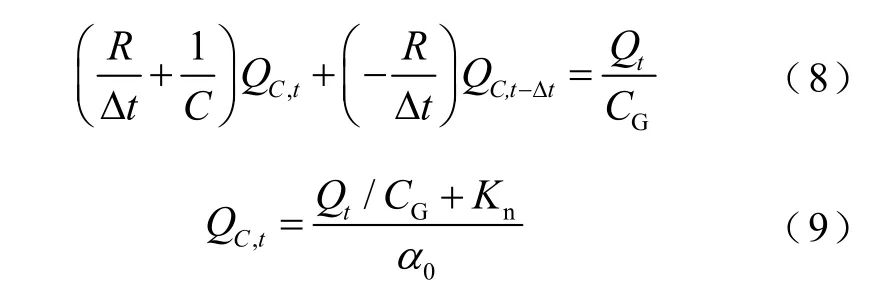
其中

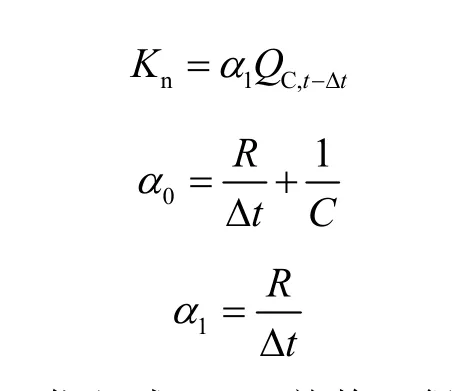
因此，将式（9）代入式（2）并整理得

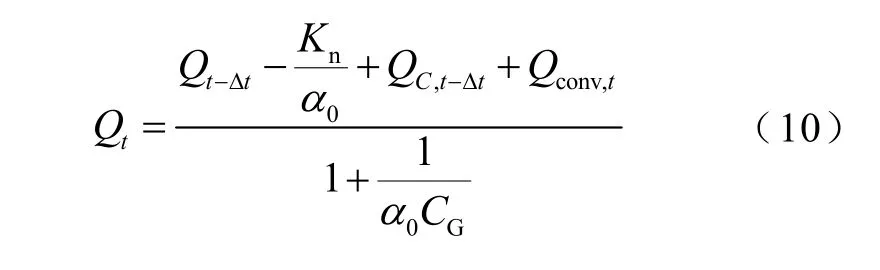
3 电极等效电容CG计算

设两电极间电势为U，两电极组成间距为D的平行板电容，其等效电容为CG，电极间存储的电场能量为

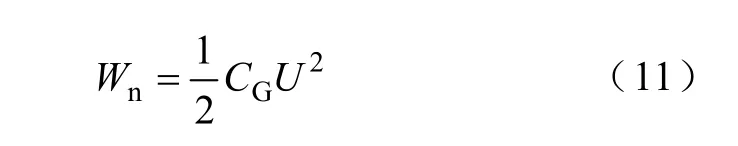
由于两极板电场是均匀的，因此有

电极等效电容为

式中，ε0和εr分别为真空介电常数和极板间介电常数，将式（12）和式（13）代入式（11）得

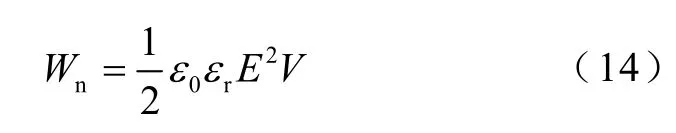
式中，V为极板电容器中电场遍及的体积。

固定金属电极板电势为1.0V，利用电场强度计算电极间每个网格的电场能并求和得到总电场能Wn总为

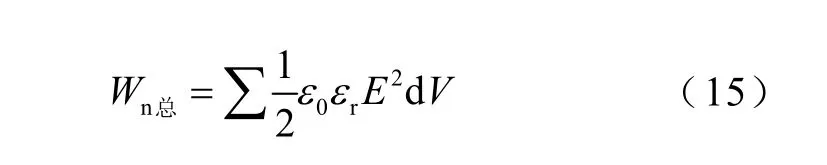
由式（13）和式（15）可求得等效电容为

在仿真区域坐标零点取为左边界，参考零电位为右边界，空间场强分布如图3所示。图3中放电板间距方向网格尺寸为 Δx，t时刻左极板的电势大小为φt( 0)=φ0,t，距离左边界一个网格位置处的电势大小为

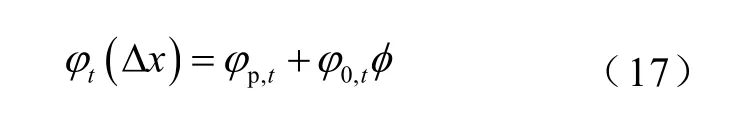
式中，φp,t为极间电压为零时等离子体产生的电势值；φ0,t为t时刻左极板的电势值；φ为电极两端电动势。 电场也有相同关系式为

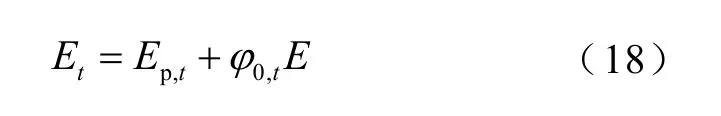
式中，Et为单位电压时的电场强度；Ep,t为极间电压为零时等离子体产生的电场强度；E为仿真区域的电场强度值。

根据图3，由高斯定理得

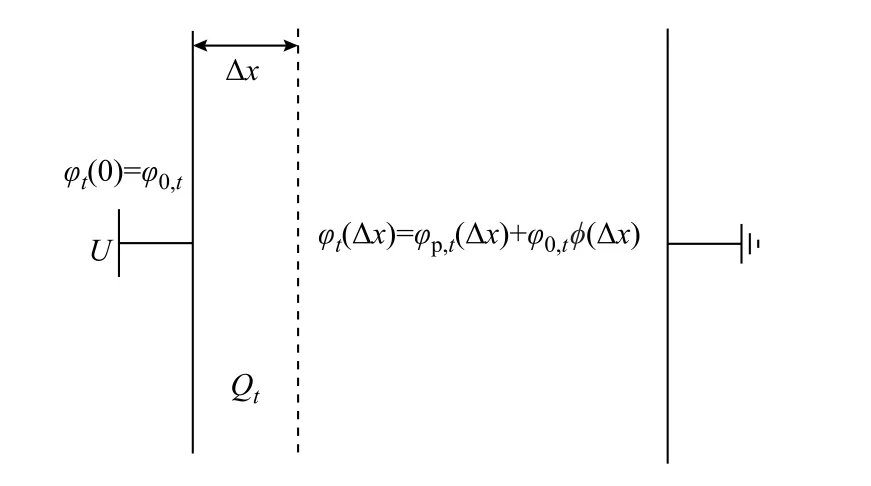
图3 空间场强分布Fig.3 Spatial field strength distribution

式中，σ为面电荷密度。

通过对式（18）中的电场进行差分计算，积分之后即得到求解t时刻放电极板上存储的电荷量方程为

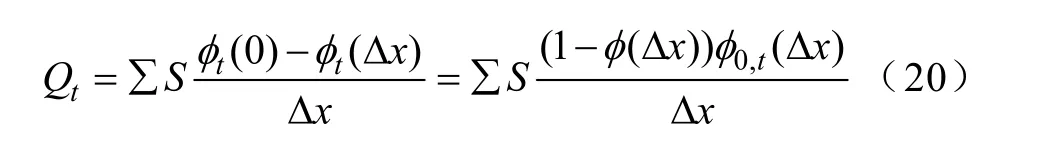
式中，S为仿真的放电板的极板面积。

仿真过程中求解电荷的具体实现步骤如下：

（1）在静电模型中计算极间电压为1V时的电势分布，并将电场分布存储为E0。

（2）计算极间电压为0V时，等离子体电势分布φp,t。

（3）迭代方程为式（10）。

仿真从t=0s开始，并初始化Qt、Qt-Δt、QC,t、QC,t-Δt，通过记录电极上的沉积电荷，即可得到Qconv,t。（4）根据式（9）和式（6）即可求出φ0,t。

（5）再利用等离子体电场强度Ep,t与电极两端电势φ0,t，以及与φ0,tE叠加的电场来推空间粒子的运动，电场计算式见式（18）。

（6）最终，将Qt赋值给Qt-Δt，QC,t赋值给QC,t-Δt，如此循环进行下一步迭代。

4 PIC静电模型

本文采用的是静电模型，带电粒子在空间电场和带电粒子形成的自洽电场的作用下运动到新的位置，获得新的速度。粒子运动依旧符合经典运动学方程，其运动方程可以表示为

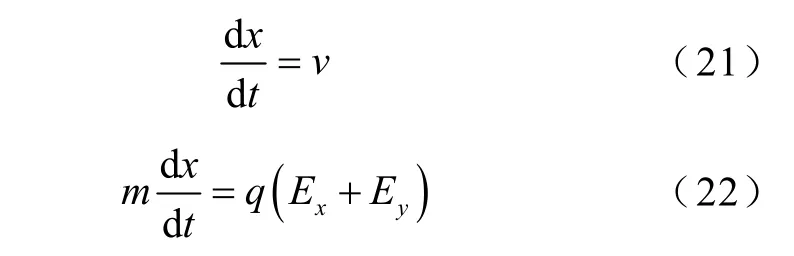
式中，m和q分别为带电粒子的质量和电荷；Ex、Ey为空间中x方向、y方向上的电场强度。

由于蛙跳格式具有能量守恒的特点，在给定初始条件下可以利用显示蛙跳格式求解方程式（21）、式（22）的粒子速度和位移，蛙跳法示意图如图4所示。

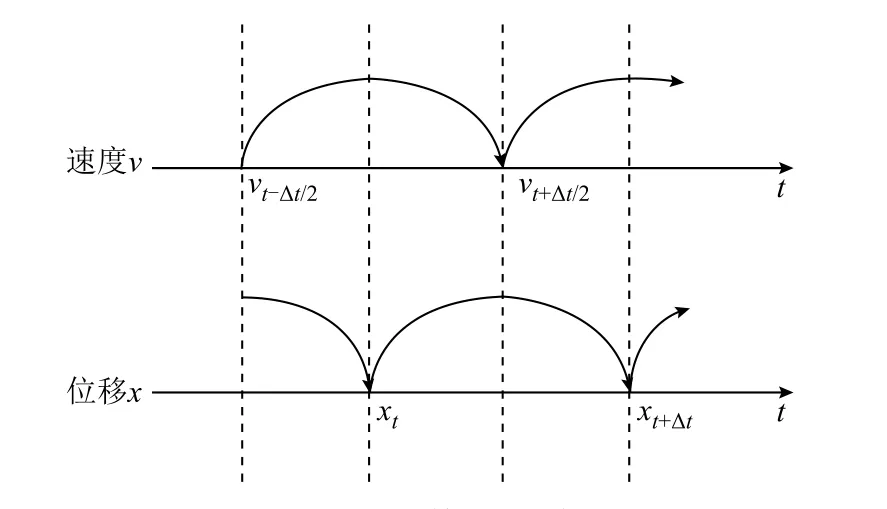
图4 蛙跳格式示意图Fig.4 Leapfrog format diagram

在经过∆t时间后，带电粒子的最新位置和速度的离散方程如式（23）和式（24）所示，对所有带电粒子重复计算即可得到下一个时刻的位置和速度。

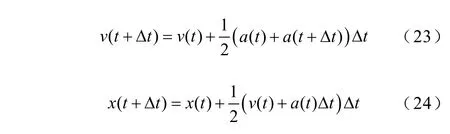
式中，v(t+Δt)和x(t+Δt)分别为电子运动时间 Δt后的速度和位置；a(t+Δt)为时间 Δt后的电子加速度。

在静电模型中，通过求解泊松方程就可以得到空间电场和电势的分布，且泊松方程为

式中，ρ为电荷密度；ε为介电常数；φ为空间电势。

求解过程中的网格形式如图5所示，由于模拟划分的网格并非等间距的正方形，文中将采用紧致修正法求解泊松方程。

图5 网格示意图Fig.5 Schematic diagram of grid

先将式（25）进行修改为

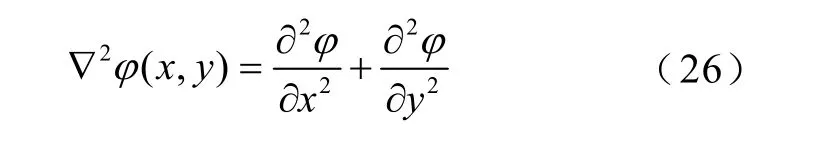
从图5中可以得到网格间距∇xi=xi-xi-1，∇y=yi-yi-1，再通过构造紧致修正法所需要的中心差分格式，如式（27）、式（28）所示。

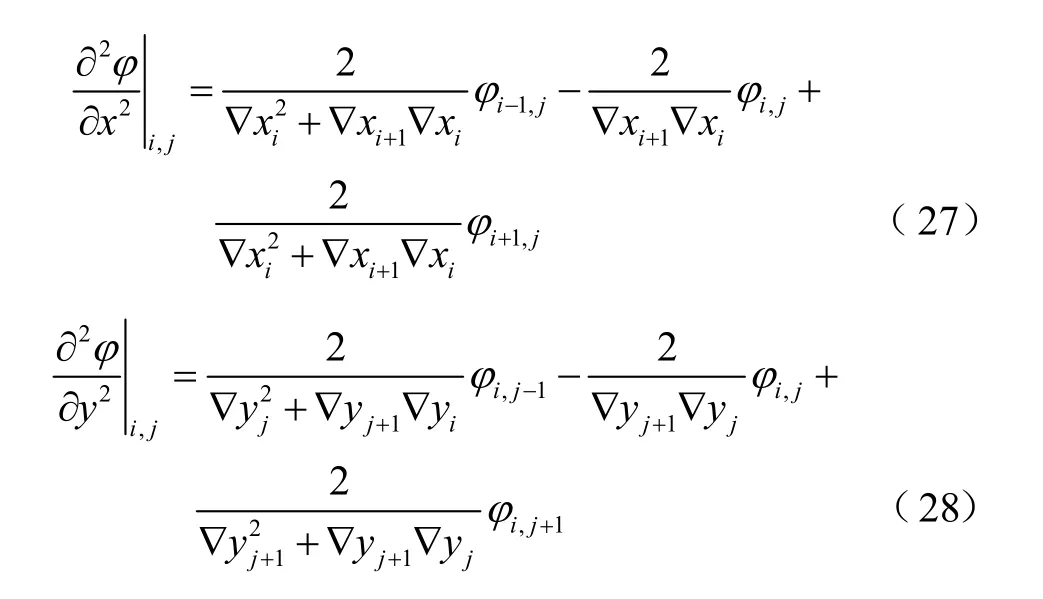
将式（27）和式（28）一起代入方程式（26）整理后可得

由粒子运动方程求解得出电荷q，代入式（30）得到ρ，最后由式（29）即可求解泊松方程。

PIC/MCC粒子法模拟流程如图6所示。

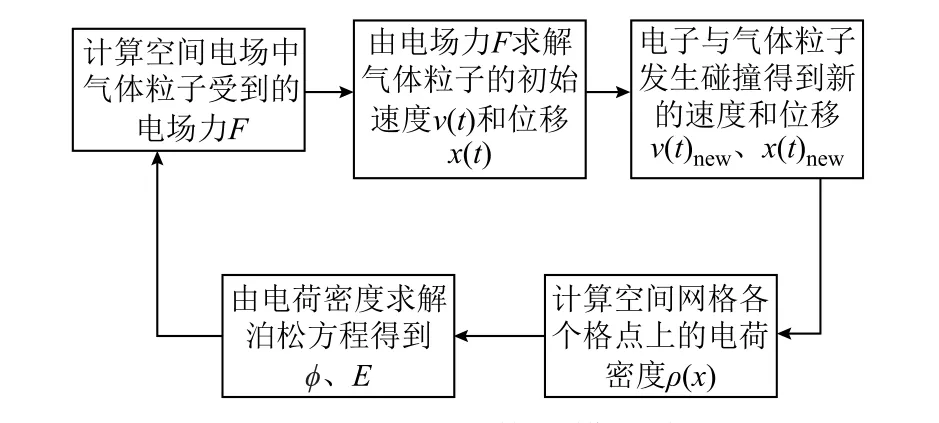
图6 PIC/MCC数值模拟流程Fig.6 PIC/MCC numerical simulation flowchart

本文模拟中将考虑粒子之间的弹性碰撞和非弹性碰撞，例如电子激发、电离碰撞、电子吸附等，主要反应方程式见表1。

表1 反应方程式Tab.1 Reaction equation

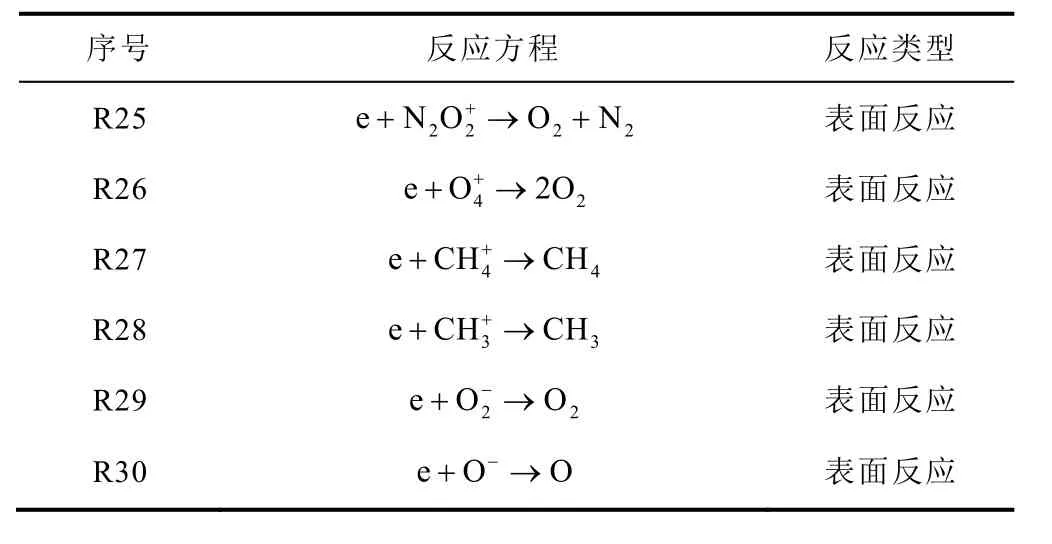
（续）

5 仿真结果的分析

5.1 极间电压对微间隙短路放电的影响

为了研究不同极间电压对微间隙短路放电的影响，首先固定平行板间距为1μm，外接电容容值为30pF，分别对18V、24V、30V极间电压情况下的放电空间进行仿真计算，极间电压及极间电流变化曲线如图7所示。

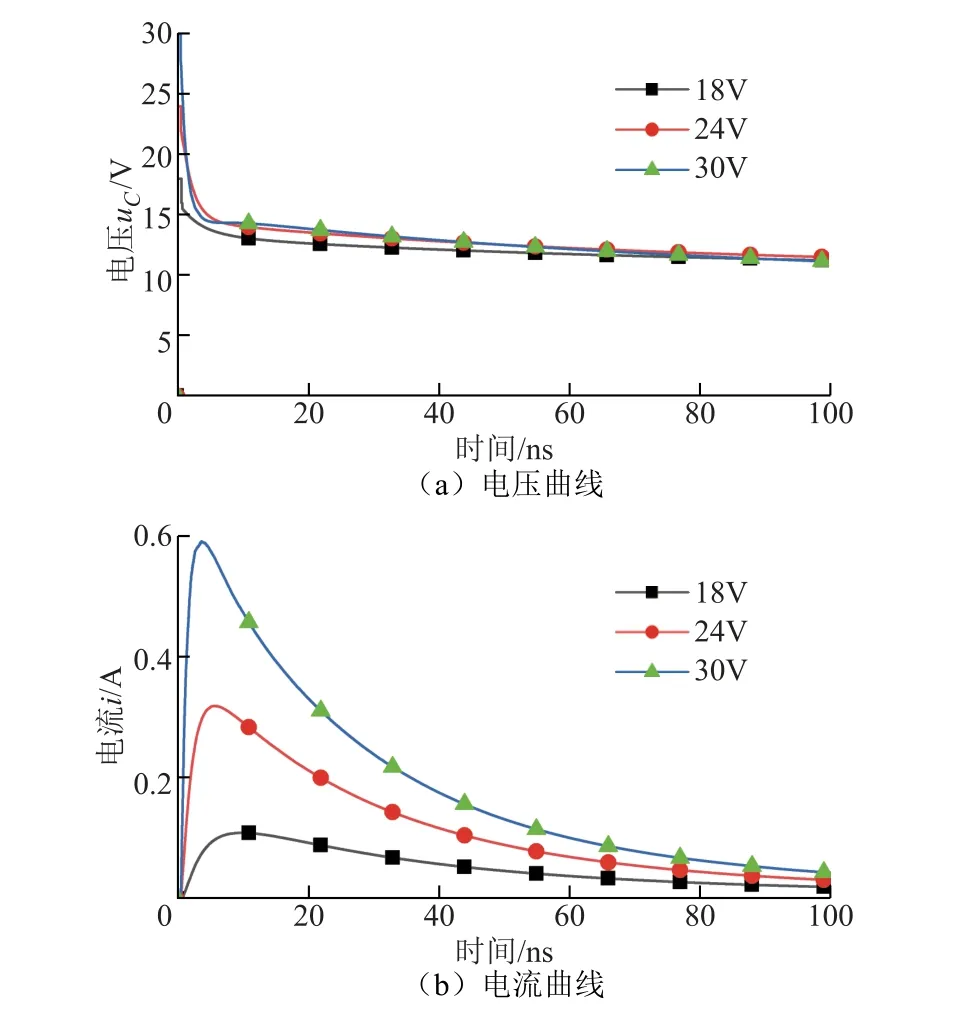
图7 不同电压下极间电压电流变化曲线Fig.7 Voltage and current curves between electrodes under different voltages

从图7a可以看出，改变电极两端电压，气体电离达到稳态时平行板极间电压总维持在11V左右，由此可见，当极间距固定，气体电离达到稳定后，极间电压维持一定值；从图7b中可以看出，随着电极电压增大，极间电流也变大。从图7中电压、电流变化曲线可以发现，当极间距为1μm，间隙介质击穿时间与极间电压无关，不同电压下，所用时间均为7ns，而火花产生阶段是7～30ns，该阶段由于火花电阻的增大，极间电流开始逐渐减小，极间电压继续下降，直到极间电流减小到刚好能使放电达到一个稳态。由于该模型电极间距固定，不会出现电极闭合的情况，因此放电模拟过程无火花熄灭阶段。

不同电压下微间隙气体粒子数变化曲线如图8所示。通过图8对比发现，随着极间电压的不断增大，甲烷和空气所电离出的正负离子总量整体呈增加的趋势。在7ns之前由于平行板放电处于介质击穿，混合气体发生电离，从而产生大量粒子。从图8a可以观察到，极间电压为18V时，气体粒子数：O2＞CH4＞N2；从图8b和图8c可以看出，当电压为24V、30V时，气体粒子数：N2＞O2＞CH4，N2粒子数量随着电压增大，由2×105增加到1.5×108，相对于其他气体粒子，N2粒子数变化最大。可见随着极间电压的不断增大，电场强度对N2的电离影响大于O2和CH4。

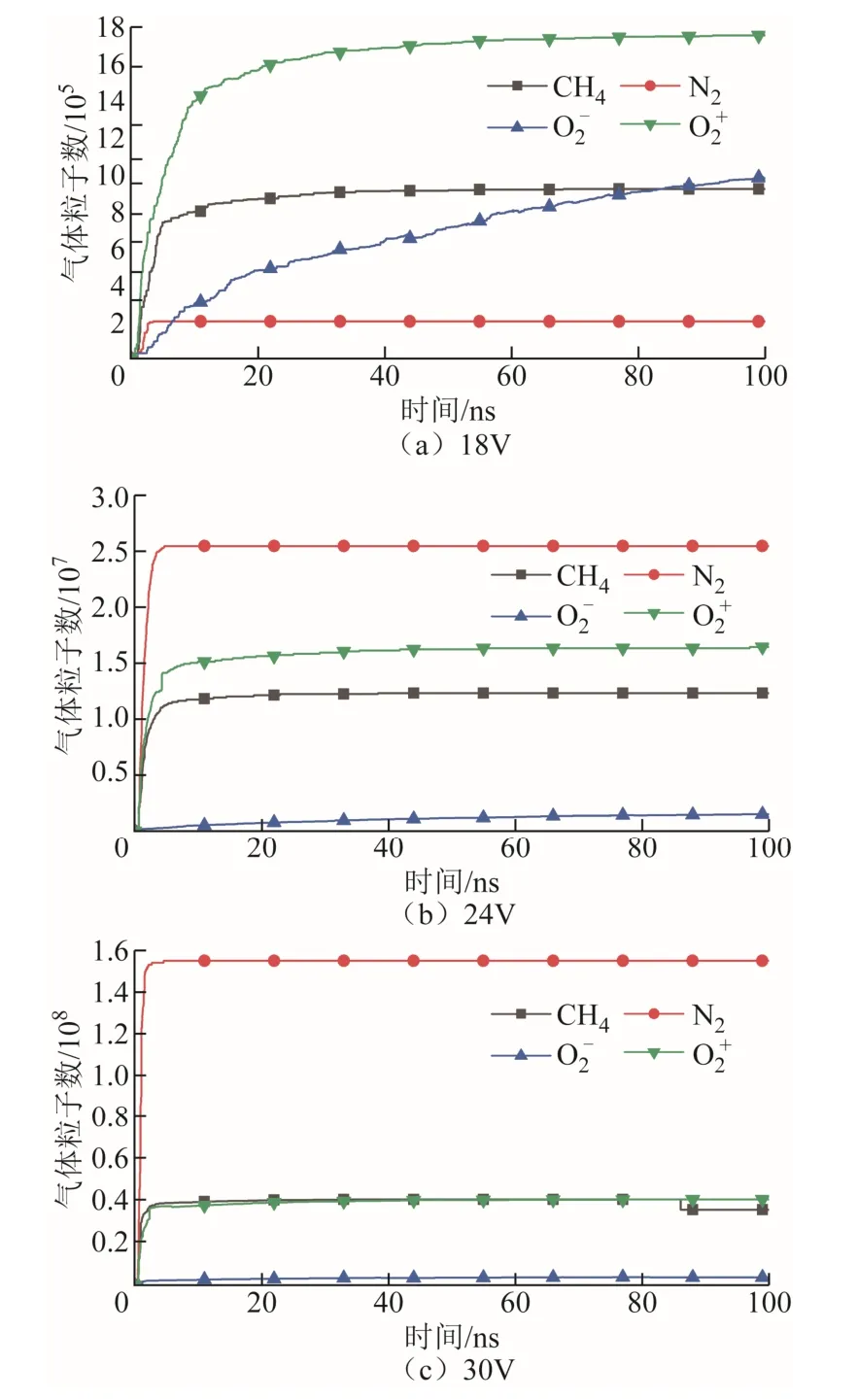
图8 不同电压下微间隙气体粒子数变化曲线Fig.8 Variation curves of micro-gap gas particle number under different voltages

不同电压下空间电子数变化曲线如图9所示，不同电压下平均电子能量对比曲线如图10所示。从图9可以明显看出，在间隙介质击穿阶段，由于场致发射，电子快速增多，与混合气体的分子发生各种碰撞反应，因此，在相同电压下，产生的电子数可以达到109数量级。从图10中对比可知，当极板施加的电压发生改变时，空间的平均电子能量也不同。在间隙介质击穿阶段，由于阴极表面产生大量的电子，平均电子能量也在不断增加；随着极间电压的增大，空间中电子能量也会增大。因此，极间电压越高，火花产生阶段所消耗的能量越大，平均电子能量减少幅度也就越大，当气体电离达到稳定时，平均电子能量为5eV。由此可见，随着电场强度的不断增大，气体电离时对平均电子能量的消耗也越大。

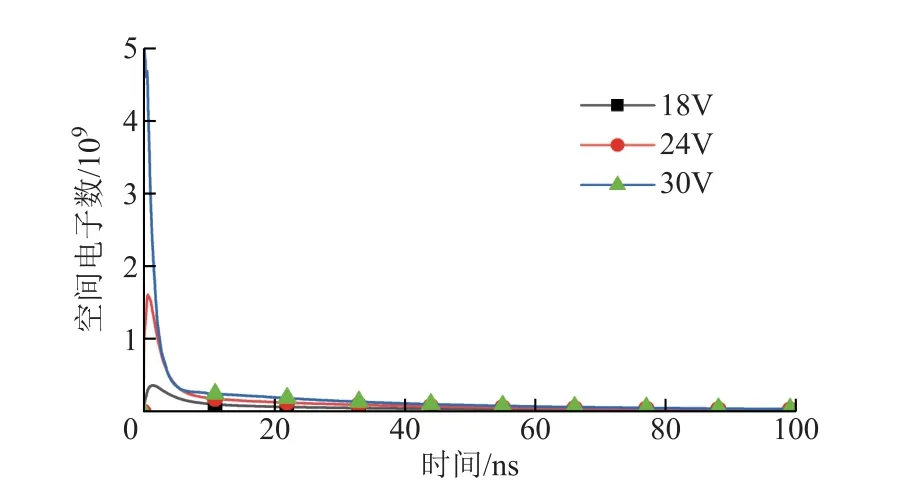
图9 不同电压下空间电子数变化曲线Fig.9 Variation curves of space electron number under different voltage

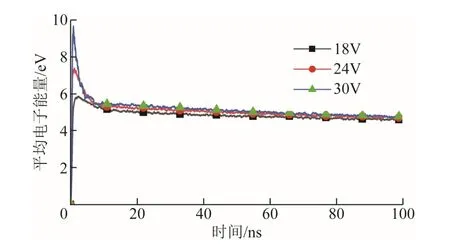
图10 不同电压下平均电子能量对比曲线Fig.10 Comparison curves of average electron energy under different voltages

5.2 极距对微间隙短路放电的影响

为了研究不同极距对微间隙放电的影响，分别取极距为1.0μm、1.5μm、2.0μm，极间电压30V，电容为30pF，对放电模型进行仿真计算。不同极距下极间电压、电流变化曲线如图11所示。

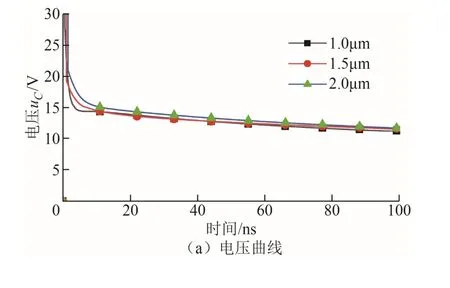
从图11a中可以看出，当放电达到稳态时，不 论电极间距为多少，极间电压最终均稳定在11V，可知放电达到稳态后的极间维持电压与电极间距无关；从图11b可以看出，当极间电压固定时，随着极距的增大，电场强度变小，介质击穿时间在逐渐增长，因此，极距越大，气体介质击穿时间越长，会越难以击穿。

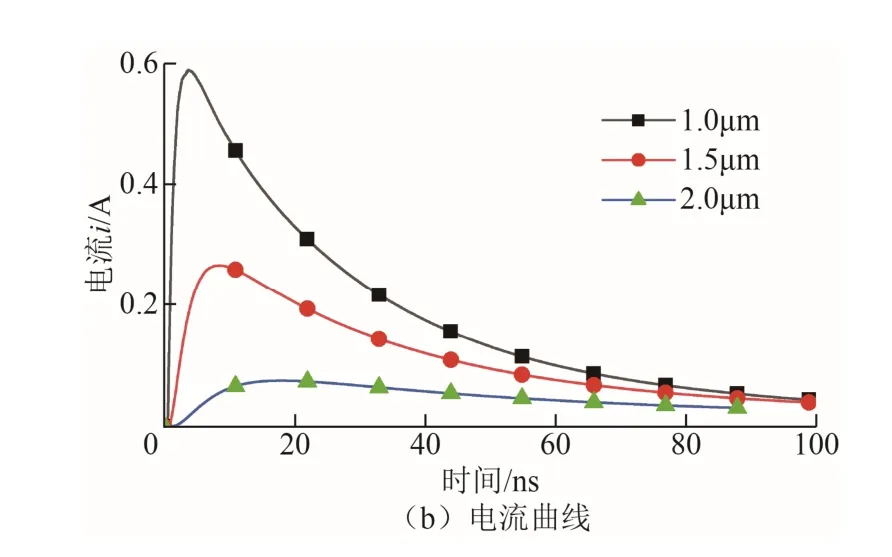
图11 不同极距下极间电压和电流变化曲线Fig.11 Variation curves of voltage and current between poles under different pole pitch

不同极距下微间隙气体粒子数变化曲线如图12所示。从图12中可以很容易看出，电容两端电 压相同时，随着极间距增大，空间电场强度逐渐减小，混合气体电离出正负离子总量整体呈减少的趋势，但减少的幅度很小，气体电离的粒子数总是：N2＞O2≈CH4，可见极距对气体电离的影响远小于电容两端电压对气体电离的影响；在介质击穿之后，1μm极距下，气体粒子总量的变化比极距为1.5μm、2.0μm时更加稳定，因此，随着极距的增大，气体粒子运动距离更大，气体介质击穿时间也更长。

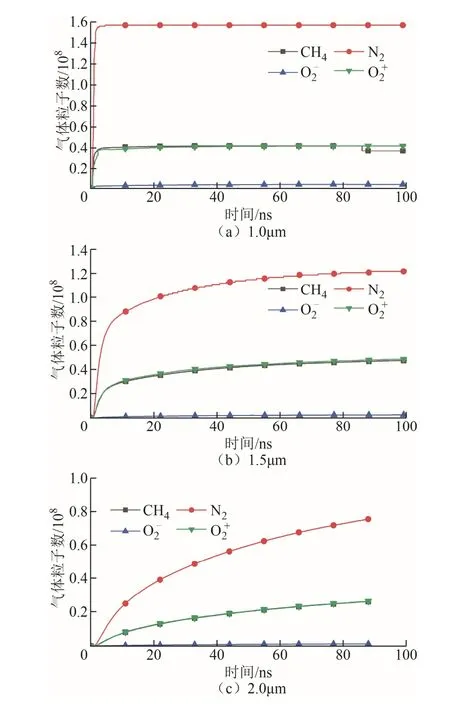
图12 不同极距下微间隙气体粒子数变化曲线Fig.12 Variation curves of micro-gap gas particle number under different polar distances

不同极距下空间电子数变化曲线如图13所示。由图13可知，当极距增大时，空间电场强度会随之减小，从而导致空间电子数急剧下降，进而影响电子能量。从图14可以看出，随着极距减小，击穿阶段产生平均电子能量增加速率变快，电子能量峰值也越高，在1μm时，平均电子能量峰值可以达到10eV。当极距变小时，火花维持阶段下的平均电子能量也随之变小，这是因为，随着电场强度的增大，气体的电离程度也会增强，将会消耗更多的电子能量，因此，在火花维持阶段时，极距越大，空间中剩余的电子能量也越多。

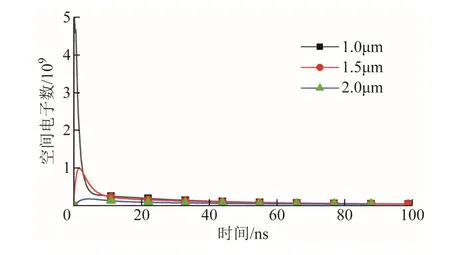
图13 不同极距下空间电子数变化曲线Fig.13 Variation curves of space electron number under different polar distance

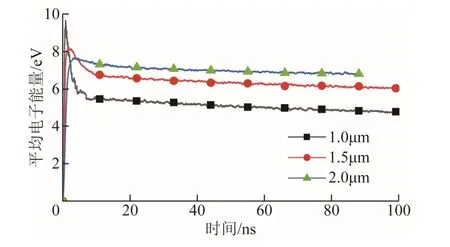
图14 不同极距下平均电子能量对比曲线Fig.14 Comparison curves of average electron energy under different polar distances

5.3 容值大小对放电的影响

为了研究容值大小对微间隙短路放电的影响，仿真时，极间电压为24V，极距1μm，分别取电容为10pF、30pF、82pF，得到极间电压、电流变化曲线，如图15所示。

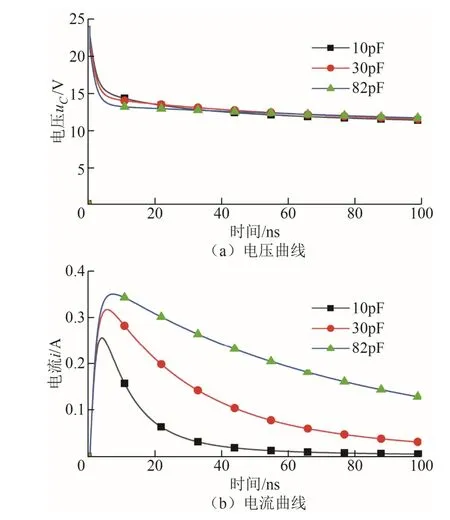
图15 不同外接电容下极间电压电流变化曲线Fig.15 Variation curves of voltage and current between electrodes under different external capacitors

图15a中可以看出，随着外接电容的不断增大，放电达到稳态时极间电压也维持在11V；从图15b中可以看出，随着外接电容的增大，极间电流也会增大，这是因为在相同电压下，电容值增大后，电容所储存的电荷量增大，导致回路电流增大。可见电容大小也会影响到气体介质击穿的时间，但其影响程度是小于极距对该阶段的影响，而在火花产生 阶段，电容储存的电荷量随着容值的增大而增大，因此，极间电流也会随之增大。

不同外接电容下微间隙气体粒子数变化曲线如图16所示。从图16中的对比可以看出，外接电容的改变不影响爆炸性混合气体电离出的气体粒子总量，其中，N2粒子数一直处于2.5×107，氧气粒子则是由氧气负离子和氧气正离子组成，其总量与甲烷气体粒子相等，约为1.5×107。可见，微间隙短路放电时电流主要由N2粒子贡献，而O2和CH4的电离对放电时电流的贡献相当。

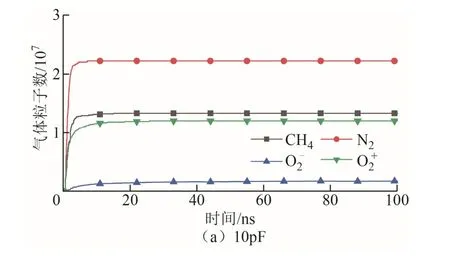
图16 不同外接电容下微间隙气体粒子数变化曲线Fig.16 Variation curves of micro-gap gas particle number under different external capacitors

不同外接电容下空间电子数变化曲线如图17 所示。从图17可以看出，在介质击穿阶段，阴极表面电子的形成不会随着外接电容的改变而改变，在火花产生阶段和维持阶段，随着外接电容容值改变，其空间电子数峰值均达到1.6×109。不同外接电容下平均电子能量对比曲线如图18所示。从图18中可以得到，容值不会影响平均电子能量的大小，在24V、 1μm时，平均电子能量峰值均为7.5eV，当放电处于稳态时，随着电容的增大，平均电子能量均在5eV左右。因此外接电容的大小不是影响平均电子能量的主要原因。

图17 不同外接电容下空间电子数变化曲线Fig.17 Variation curves of space electron number under different external capacitors

图18 不同外接电容下平均电子能量对比曲线Fig.18 Comparison curves of average electron energy under different external capacitors

6 实验验证

为了验证仿真模型的正确性，本文将基于IEC标准火花试验装置，在浓度为8.5%的甲烷和空气混合气体环境下对33μF、不同电压以及24V、不同外接电容的电路进行电容短路放电实验研究，实验平台如图19所示。

图19 IEC火花放电实验平台Fig.19 IEC spark discharge test platform

该实验平台将使用RIGOL MSO5354数字示波器（带宽为350MHz，采样频率为4GS/s）、RIGOL PVP2350无源探头、RIGOL电流探头进行测量，最终采集的典型放电电压、电流波形如图20所示。图20a为不同电压下火花放电时的电压和电流波形，从图中可以看出，随着电容端电压增大，极间电流也随之增大，但火花维持电压均为11V左右。图20b为不同电容下火花放电时电压、电流波形，从图中可以看出，随着外接电容的增大，极间电流也会随之增大，且放电时间也会增长。

从图20可以看出，火花试验过程中，电极不断地运动，随着两电极不断靠近，极间电场强度不断增强，导致极间介质击穿，放电电流迅速增大，电 极两端电压迅速下降；随着电流快速上升，介质被击穿时产生的大量电子开始向阳极移动，移动过程中，电子与气体分子不断发生碰撞、电离，产生新的电子和正离子，受激发的粒子产生光子，致使极间开始产生放电火花，之后火花电阻逐渐增大，火花电流越来越小，放电电压则继续按一定规律下降，此时为火花产生阶段；直到电极提供的电流减小到刚好能使放电火花维持时，进入火花维持阶段；火花维持阶段结束后两电极彻底闭合，极间电压由维持电压下降到零。由于电容中残存的能量释放，电流又出现第二个峰值，但电极已闭合，能量由电路中电阻和电极吸收，该过程为火花熄灭阶段。

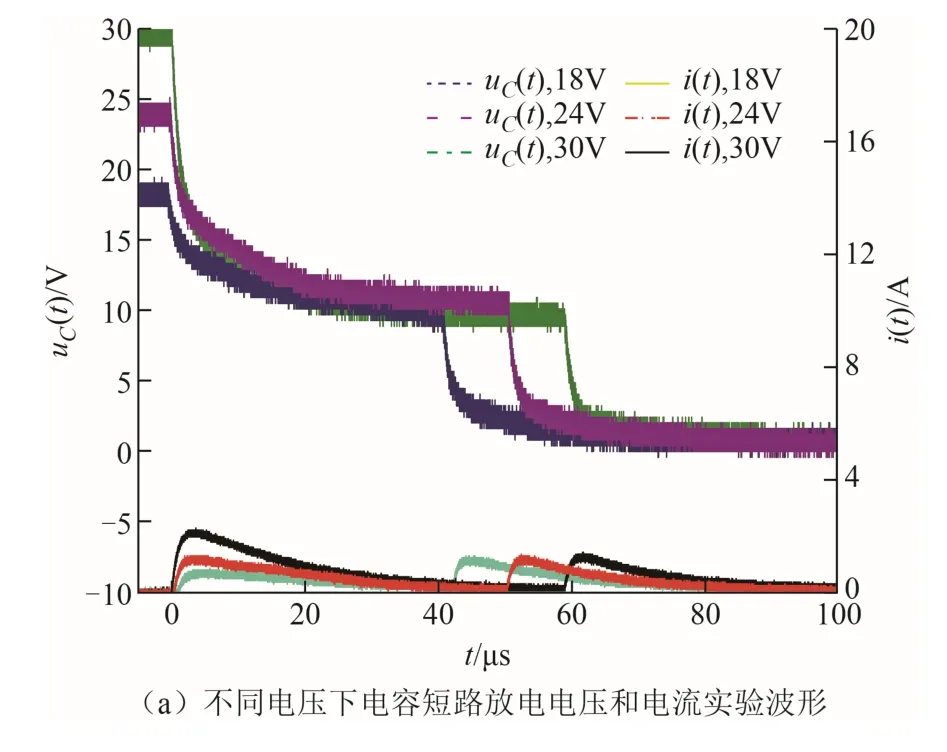
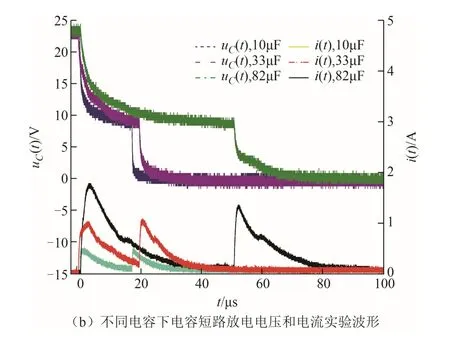
图20 电容短路放电电压和电流的实验波形Fig.20 Experimental waveforms of capacitor short-circuit discharge voltage and current

在火花试验过程中两个电极相互运动，因此电容短路时存在二次放电现象，而本文为静态仿真模型，主要针对电容短路放电的一次放电阶段进行模拟，因此没有二次放电和火花熄灭阶段。通过对比实测波形和仿真曲线，可知在电容放电期间，放电电流和电压的实测波形和仿真曲线趋势吻合较好，只是放电时间有所差距，这是因为对本文所用的仿真模型放电进行计算时工作量大，计算周期较长，对计算机的运行速度要求较高。为了缩短仿真周期，仿真模型中的电容值为pF级，因此放电时间要比实测中μF级电容放电时间短。因此，本文所建立的基于电荷等效法的电容短路放电模型不仅能够模拟电容放电过程并得到与实验一致的放电电压、电流的变化趋势，而且能从微观方面解释电容短路放电过程中粒子的运动情况，为研究电容短路放电机理提供了新的参考。

7 结论

本文研究了IEC火花试验装置容性电路短路放电的微观特性，分析了极间电压、极间距以及外接电容对微间隙电容短路放电的影响，得到以下结论：

1）IEC火花试验过程中随着极间电压的增大，空间平均电子能量也逐渐增大，且极间电压对N2的电离影响程度远大于对O2和CH4的电离。

2）火花试验装置电极间距变大时，击穿所需要的时间变长，电极间气体介质越难以击穿，且在放电过程中，对于电子能量的消耗也会逐渐减小。

3）在容性电路短路放电过程中，容值的改变对气体电离基本不会产生影响，而击穿后的极间电流会随着电容的增大而增大。

4）平均电子能量主要与极间电场强度有关，随着极间电场强度增大，气体电离越剧烈，电流密度会越大，平均电子能量也会逐渐变大。