面向小偏置碰的轮毂断裂模拟研究

郑 颢 欧阳俊 王玉超 李 伟 曾子聪 黄 毅 刘 衡

广州汽车集团股份有限公司汽车工程研究院，广州，511434

0 引言

随着中国保险汽车安全指数C-IASI的推广，尤其是25%小偏置碰极端恶劣工况的引入，整车碰撞会发生大面积钣金和焊点撕裂，底盘件、轮辋和轮毂断裂等情况。车轮总成作为小偏置碰的重要碰撞力传递路径之一，轮毂(含轮毂中心、轮辐和轮辋)刚度对碰撞结果的影响极大[1-2]。在小偏置碰工况中，轮毂受到过大的碰撞力会发生断裂失效，现阶段碰撞仿真主要采用刚性轮毂模拟，这种建模方式不能表征轮毂结构的碰撞断裂和轮胎偏转运动，且刚性轮毂对门槛梁冲击过大时会导致门槛的变形失真，从而影响小偏置碰的仿真精度。目前国内外对轮毂小偏置碰下的断裂失效模拟研究均处于起步阶段，为获得小偏置碰的稳健模拟预测结果，需开展材料特性和失效模型的力学性能研究。为准确地模拟轮毂在碰撞过程中的塑性变形和断裂失效，仿真模拟不仅需要描述材料的弹塑性行为，也要对材料断裂的力学行为进行描述。材料的失效应变与应力状态(可用应力三轴度或应变比描述)和应变率相关，而采用将单轴拉伸试验的断裂延伸率作为失效判据的常应变单元失效方法来描述材料断裂显然是片面的，预测结果是不准确的[3-6]。

随着力学理论和有限元模型的发展，出现了更为完善的断裂/韧性失效模型，其中Gurson模型描述了材料失效时成核成孔的现象，从正向断裂失效形成的机理对该现象进行模拟，属于典型的金属正向断裂失效模型，但该模型忽略了剪切断裂失效。CrachFEM模型同时考虑了材料的正向断裂和剪切断裂，根据不同的材料类型(如热成形钢、高强钢、挤压铝、铸铝和塑料等)，设计不同种类的材料力学试验来表征正向断裂和剪切断裂特性，可更加全面准确地预测材料的失效[7-8]。

本文基于CrachFEM断裂准则，通过材料力学试验研究了铸铝轮毂AlSi7的材料参数拟合，对比了轮毂的准静态和动态试验结果与仿真结果，验证了正向建立的CrachFEM材料卡片在模拟轮毂断裂失效的准确性。

1 铸铝AlSi7材料力学性能试验

材料的力学性能分为弹塑性和断裂失效两部分，其中材料弹塑性包括塑性硬化和屈服轨迹等。铸铝塑性硬化具有低应变率效应，但拉伸和压缩状态下铸铝应力-应变关系会有差异，需要开展准静态单轴拉伸和压缩试验获得材料的力-位移曲线，并将其转换为等效应力-等效应变关系曲线，如图1所示。

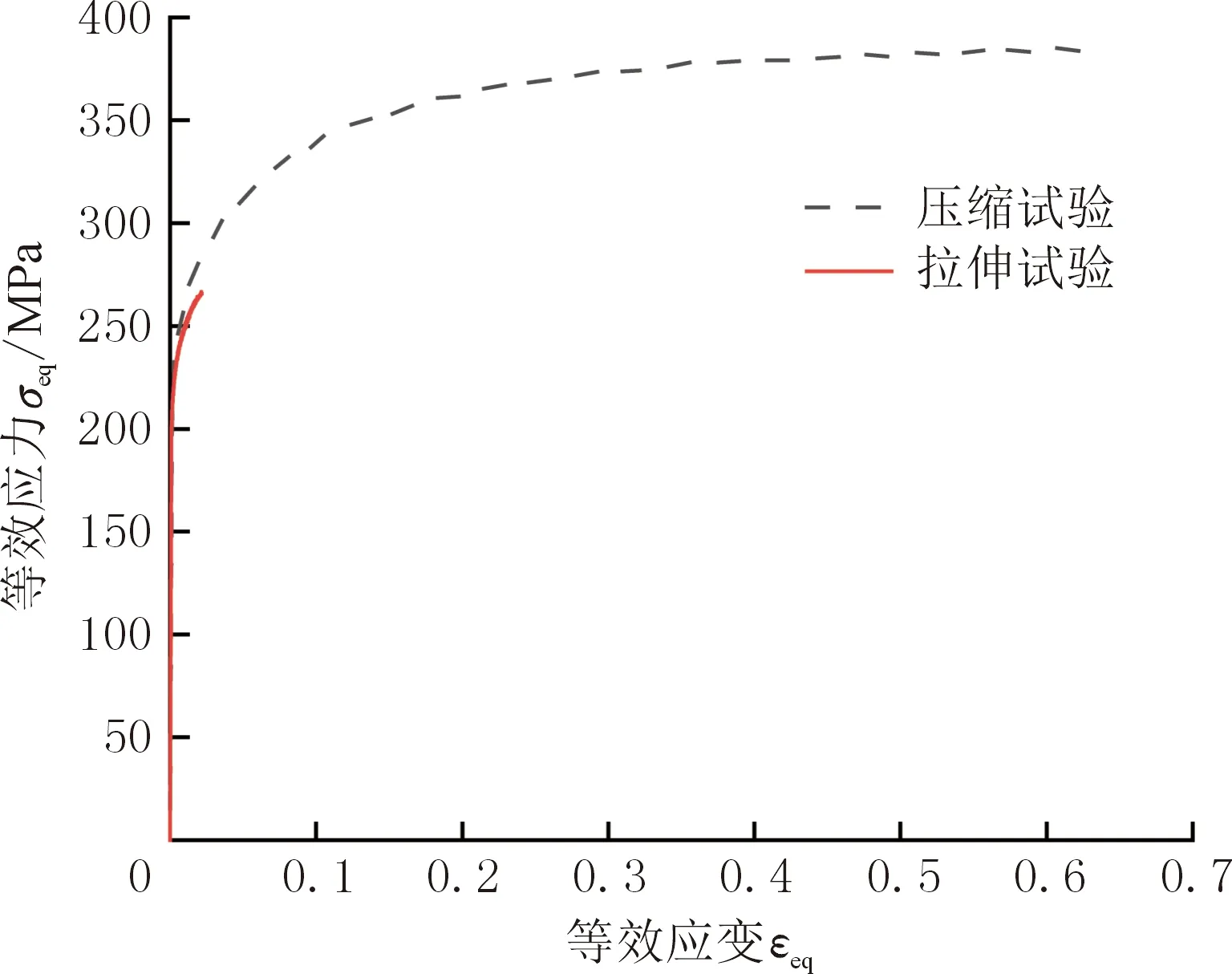
图1 AlSi7拉伸和压缩的应力-应变曲线Fig.1 Stress-strain curves in tension and compression of AlSi7

金属材料从屈服点进入塑性变形，到达抗拉点后发生成核成孔或剪切带滑移，即材料发生了损伤，损伤逐渐累积最终导致材料断裂。失效应变与应力状态有关，因此需要获得不同应力状态下的材料断裂应变。本文设计了5种试验类型，用以代表试验样件5种不同的应力状态，包括圆孔样条三点弯曲试验、宽样条三点弯曲试验、直角开槽样条拉伸试验、剪切试验和穿孔试验，完成试验后依据样件在断口区域的厚度和减薄率来计算该应力状态下的失效应变值。此外，失效应变与应变率的关系非常敏感，为更好地描述不同的应变率下铸铝材料AlSi7的断裂失效特性，本文开展了准静态(应变率为0.001 s-1)和动态(应变率为100 s-1)的材料断裂力学试验。

图2为铸铝AlSi7经过系统化材料力学试验后的样件图片，为了避免切割温度改变样件材料性能，试验样件直接从轮辋上通过水切割获得。表1所示为5组材料断裂力学试验对应的主应变比和失效模式。通过断口观察发现，试验样件的失效模式主要为正向断裂失效。

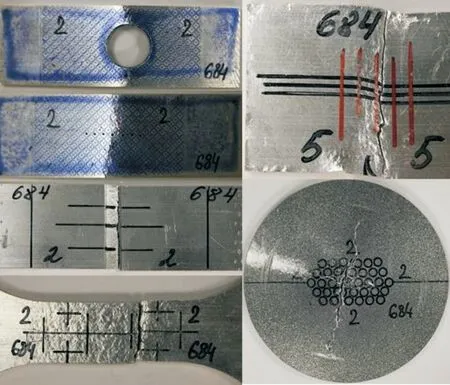
图2 AlSi7材料力学试验Fig.2 Material mechanics test of AlSi7

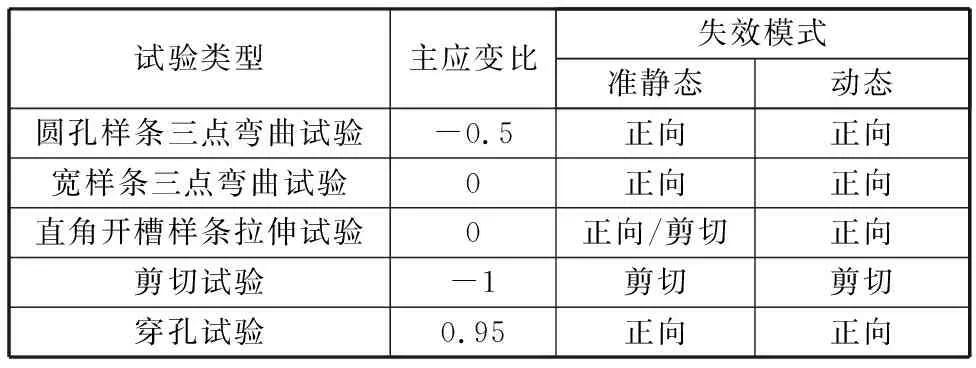
表1 材料断裂力学试验类型

2 带失效的铸铝AlSi7材料模型的开发

铸铝材料模型的开发包括塑性应力-应变曲线的拟合、各向异性屈服轨迹的修正、CrachFEM失效准则的参数拟合等。

2.1 铸铝塑性模型的开发

材料通过单轴拉伸试验而获取的塑性应变一般较小，故需要综合考虑叠层压缩或扭转试验来获取应力-应变曲线，从而确定延伸段曲线的趋势。由图1铸铝拉伸和压缩的等效应力-等效应变曲线可知，材料具有一定的拉压不对称性，将压缩曲线的纵坐标乘以缩放系数0.946后得到修正后的曲线，该曲线与拉伸曲线具有较好的一致性。

对铸铝材料进行塑性硬化准则的拟合，采用逆向标定方法对硬化段外推进行修正，常用的塑性硬化准则有Swift准则、Ghosh准则和Hocket-Sherby准则[9]。上述三种准则的具体形式分别如下：

Swift准则

σeq=A(ε0+εp，eq)n

(1)

Ghosh准则

σeq=k1(k2+εp，eq)n+k3

(2)

Hockett-Sherby准则

(3)

式中，σeq为等效应力；ε0、εp，eq分别为屈服点对应的塑性应变和等效塑性应变；σ0为屈服点的屈服应力；A、n、k1、k2、k3、c均为拟合参数，可通过数据拟合获得。

图3为基于上述三种塑性硬化准则拟合得到的应力-应变曲线，可以看出，Hocket-Sherby塑性硬化准则更加适用于AlSi7材料。

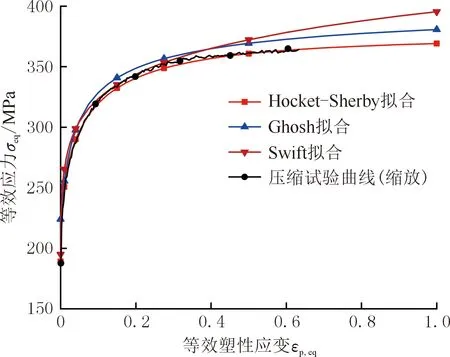
图3 AlSi7 应力-应变曲线拟合Fig.3 Stress-strain curve fitting of AlSi7

图4所示为在各向同性von Mises准则基础上修正获得的具有拉压不对称性特征的屈服轨迹，可以看出，压缩强度略大于拉伸强度。

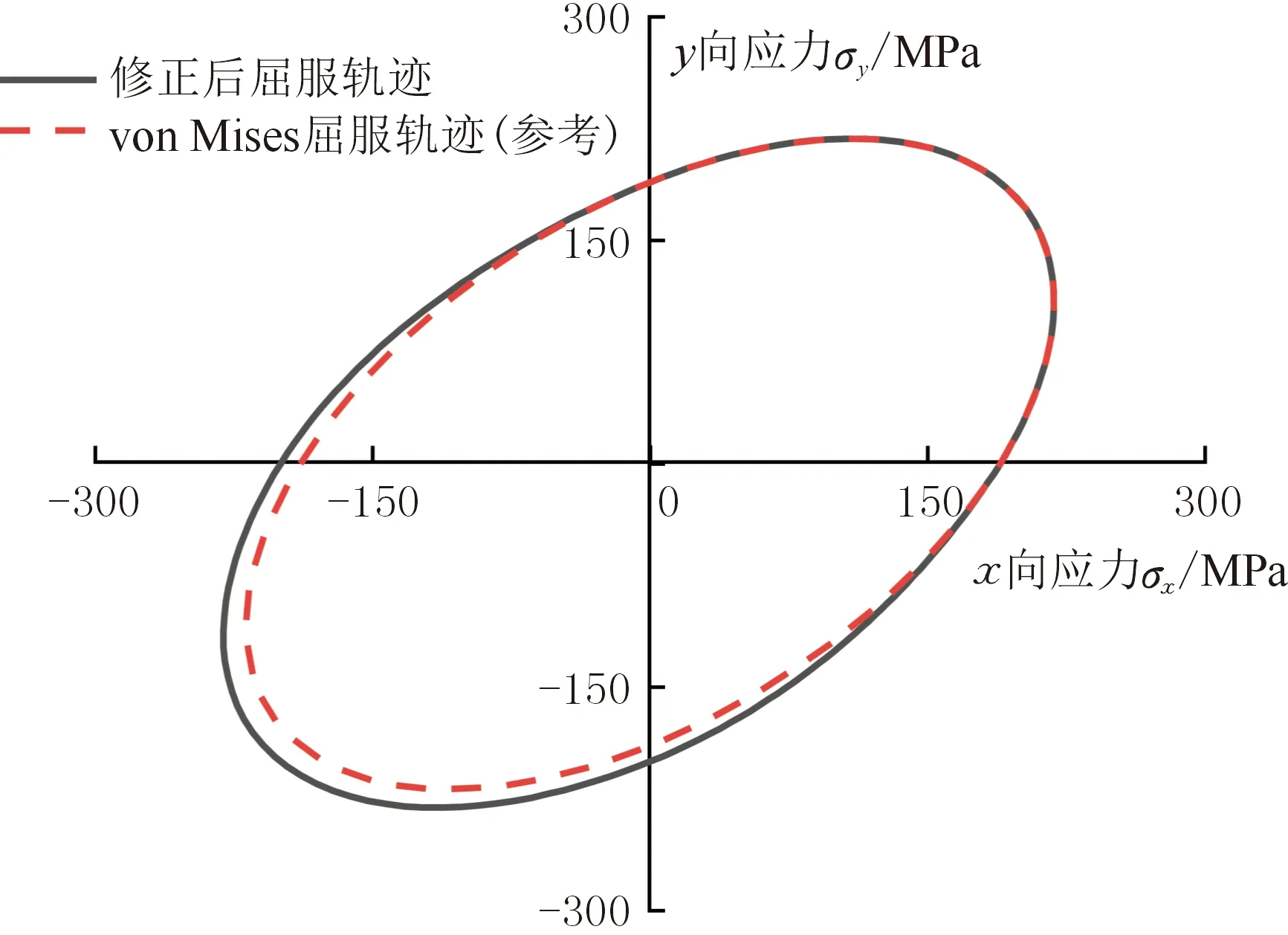
图4 AlSi7的屈服轨迹拟合Fig.4 Yield locus fitting of AlSi7

2.2 铸铝失效模型的参数辨识

在表1所示不同试验类型下测量的失效应变为离散的数据点，通过曲线拟合可获得不同应力状态下的断裂曲面或曲线。CrachFEM韧性失效准则包括正向断裂和剪切断裂。三维应力状态下，正向断裂塑性应变可表示为

(4)

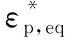
依据表1中的正向断裂失效试验数据，采用最小二乘法拟合得到参数D、q和sNF的值。该平面应力状态下的正向断裂曲线见图5，可以看出，随着应变率的增大，材料正向断裂应变呈减小趋势。这反映了铝合金材料断裂应变随着应变率的改变会有所变化的一个特性。

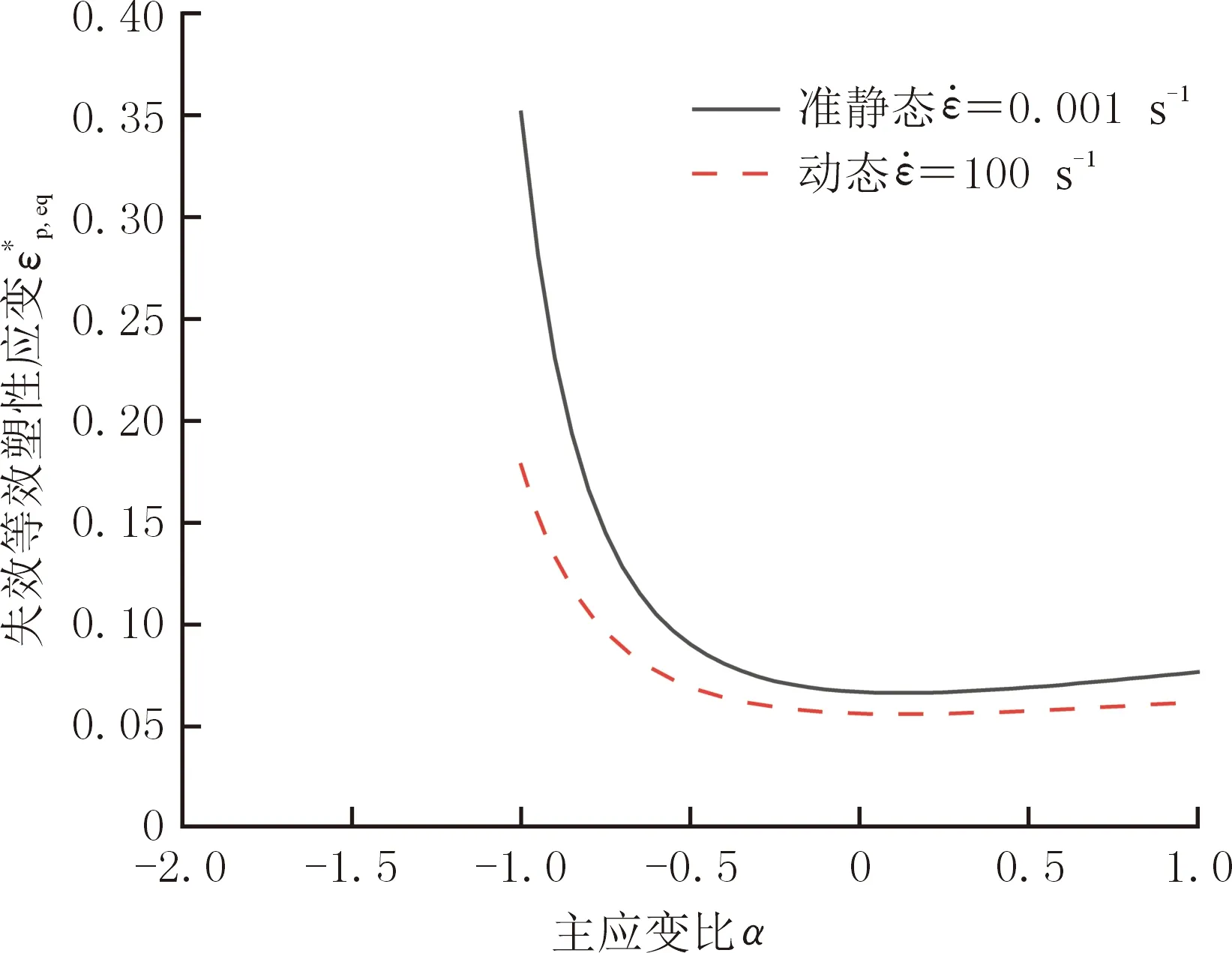
图5 AlSi7的正向断裂曲线Fig.5 Normal fracture curves of AlSi7

剪切断裂失效准则引入最大剪切应力τmax与von Mises等效应力σM的应力比，结合应力三轴度提出了三维应力表征参数，其表达式如下：

(5)

其中，kSF为材料相关的参数，则剪切失效准则可以表述为

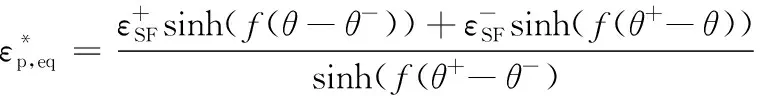
(6)

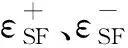
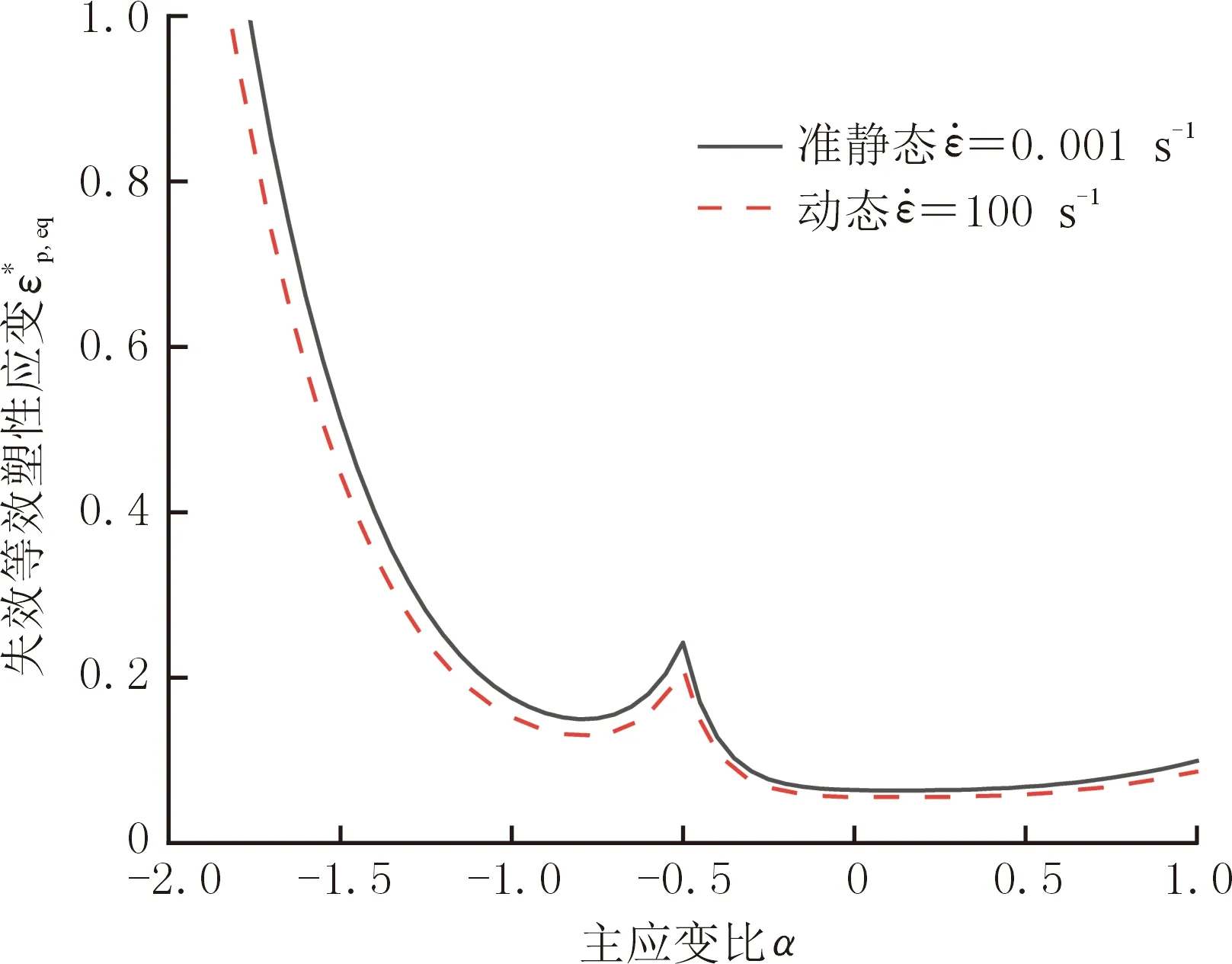
图6 AlSi7剪切断裂曲线Fig.6 Shear fracture curves of AlSi7

铸铝轮毂将以实体单元模拟为主，AlSi7材料失效模型考虑了正向断裂失效和剪切断裂失效，通过用户自定义编译实现与LS-DYNA等非线性显式求解器联合计算。对表1中材料断裂力学试验进行有限元仿真，通过力-位移曲线和断裂失效应变来验证材料卡片的准确性。

3 轮毂碰撞断裂的有限元模拟

3.1 轮毂子系统冲击试验

通过轮毂子系统冲击试验及有限元分析验证AlSi7材料卡片的准确性，同时研究最合理的轮毂有限元建模方法。小偏置碰中，常见的断裂失效有轮辋破坏和轮毂断裂，子系统试验将设计准静态试验(轮毂平板压溃试验、轮辋压溃试验)和动态试验(落锤冲击试验)，试验工装和加载位置如图7所示。准静态试验在万能试验机上完成，加载速度为5 mm/min，可获得加载力-位移曲线及试验后轮毂、轮辋断裂情况。铸铝材料的断裂失效与应变率密切相关，本文通过落锤冲击试验来验证高应变率下铸铝失效模拟的准确性。落锤冲击试验中将质量为207 kg的落锤从5 m高度自由下落撞击轮毂总成，并记录碰撞加速度-时间曲线及试验后轮毂断裂失效分布。

(a) 轮毂平板 压溃试验 (b) 轮辋压溃 试验 (c) 动态落锤 冲击试验图7 准静态压溃试验和动态试验Fig.7 Quasi-static collapse tests and dynamic tests

3.2 准静态压溃的有限元模拟

图8所示为轮毂平板压溃试验、轮辋压溃试验的有限元模型，仿真模型的工装、边界约束和加载条件与试验保持一致。主要分析单元类型和失效参数对模拟结果的影响，本文仅对轮毂平板压溃工况进行详细阐述。

(a) 轮毂平板压溃模型 (b) 轮辋压溃模型图8 准静态压溃有限元模型Fig.8 Finite element models of quasi-static collapse

铸铝结构的碰撞模拟采用实体单元，平均网格尺寸在2～4 mm，为兼顾计算时间步长要求，最小单元尺寸不小于1 mm。使用二阶四面体和六面单元进行网格划分的轮毂局部模型如图9所示，上述两种单元类型的轮毂模型单元数量分别为657 294和177 380，使用16核LS-DYNA软件计算50 ms动画仿真所需的时间分别为18 h和4.5 h，尽管六面体网格建模比较困难，但是从计算效率角度考虑，六面体单元更适合工程应用。

(a) 四面体 (b) 六面体图9 二阶四面体和六面体单元轮毂模型Fig.9 Wheel hub models with 2nd order tetra and hexahedron

平板压头与轮毂接触区域的铸铝失效对比如图10所示，可以看出，四面体在受压状态下容易产生单元失效，导致四面体轮毂与平板接触区域内的失效单元数量过多，轮毂的断裂模式与试验不符；六面体轮毂在接触区域的断裂模式与试验一致。综上，由仿真动画对比可得，六面体单元可以准确地呈现铸铝轮毂断裂失效模式，能够有效地解决四面体单元受压状态下易失效的问题。

(a) 试验 (b) 四面体 (c) 六面体图10 四面体和六面体单元接触区域的断裂对比Fig.10 Fracture comparison with 2nd order tetra and hexahedron on contact area

仿真与试验的对比发现，在仿真过程中使用六面体单元时，与半轴连接的轮毂中心不会发生断裂，但在试验过程中该轮毂中心的螺栓安装孔周围有裂纹分布。通过对轮毂中心和轮辋进行微观分析可知，这两个区域均存在铸造缩孔，但轮毂中心的缩孔孔径比轮辋的缩孔孔径大，导致轮毂中心的韧性较轮辋的韧性有所降低。由于铸造缩孔导致轮毂中心和轮辋的材料性能存在差异性，将轮毂中心和轮辋设置为相同材料的建模方式与实际不符，因此仿真模拟中需要根据铸造缩孔的影响分别定义轮毂中心和轮辋的材料特性。

由于轮毂中心和轮辋的材料差异主要来源于铸造缩孔孔径，本文从这两个区域中切割样件进行试验研究，通过对AlSi7材料正向断裂和剪切断裂曲线进行缩放处理(即将曲线的纵坐标乘以缩放系数0.55)得到轮毂中心的材料卡片，轮辋则采用不经缩放处理的AlSi7材料卡片。根据该建模方式进行仿真，对比轮毂平板压溃试验与仿真可知，加载力-位移曲线及断裂失效模式的仿真结果均与试验结果较为吻合。图11所示为轮毂平板压溃试验与仿真的加载力-位移曲线对比。经过缩放修正后，仿真和试验的加载力-位移曲线的相关性可达90%。由图11可知，两次试验的峰值力平均值为327.5 kN，仿真的峰值力为352.4 kN，预测精度达到92.4%。图12所示为轮毂平板压溃的仿真与试验对比，由于轮毂缩孔缺陷具有随机分布特性，因此两次试验的断裂位置存在差异，但断裂均集中在轮毂中心，轮毂中心的断裂位置和裂纹扩展方式在仿真结果中均有良好体现，进一步表明采用该建模方式可以可靠地模拟轮毂的断裂。

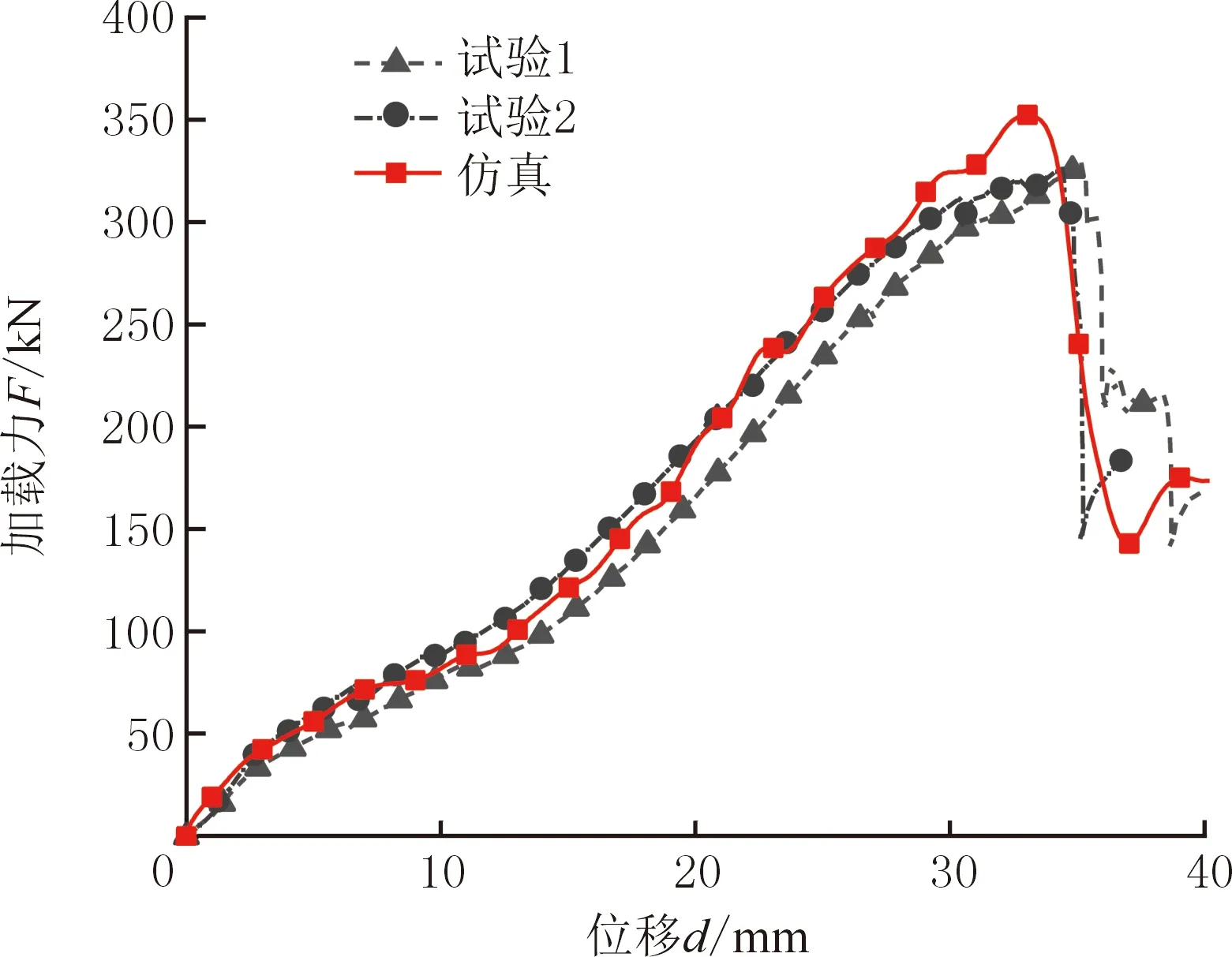
图11 轮毂平板压溃仿真与试验的加载力-位移曲线Fig.11 Force-displacement curves of simulation and test in wheel hub plate collapse

(a) 试验1图片

图13所示为采用六面体单元开展的轮辋压溃的仿真与试验对比，可以看出，仿真中裂纹起始位置和扩展方式与试验中一致。由于轮辋表面不平，轮辋压溃试验中压头滑移导致轮辋断裂位置存在差异，因此本文进行了4次轮辋压溃试验(其中3次试验的轮辋断裂位置已在图13中标出)，以验证轮辋压溃试验的稳定性。图14所示为轮辋压溃仿真与试验的加载力-位移曲线对比。经过缩放修正后，曲线相关性可达87.4%。由图14可知，4次试验的峰值力平均值为68 kN，仿真峰值力为69.6 kN，预测精度达到97.6%。

图13 轮辋压溃仿真与试验的断裂对比Fig.13 Fracture comparison of simulation and test in wheel rim

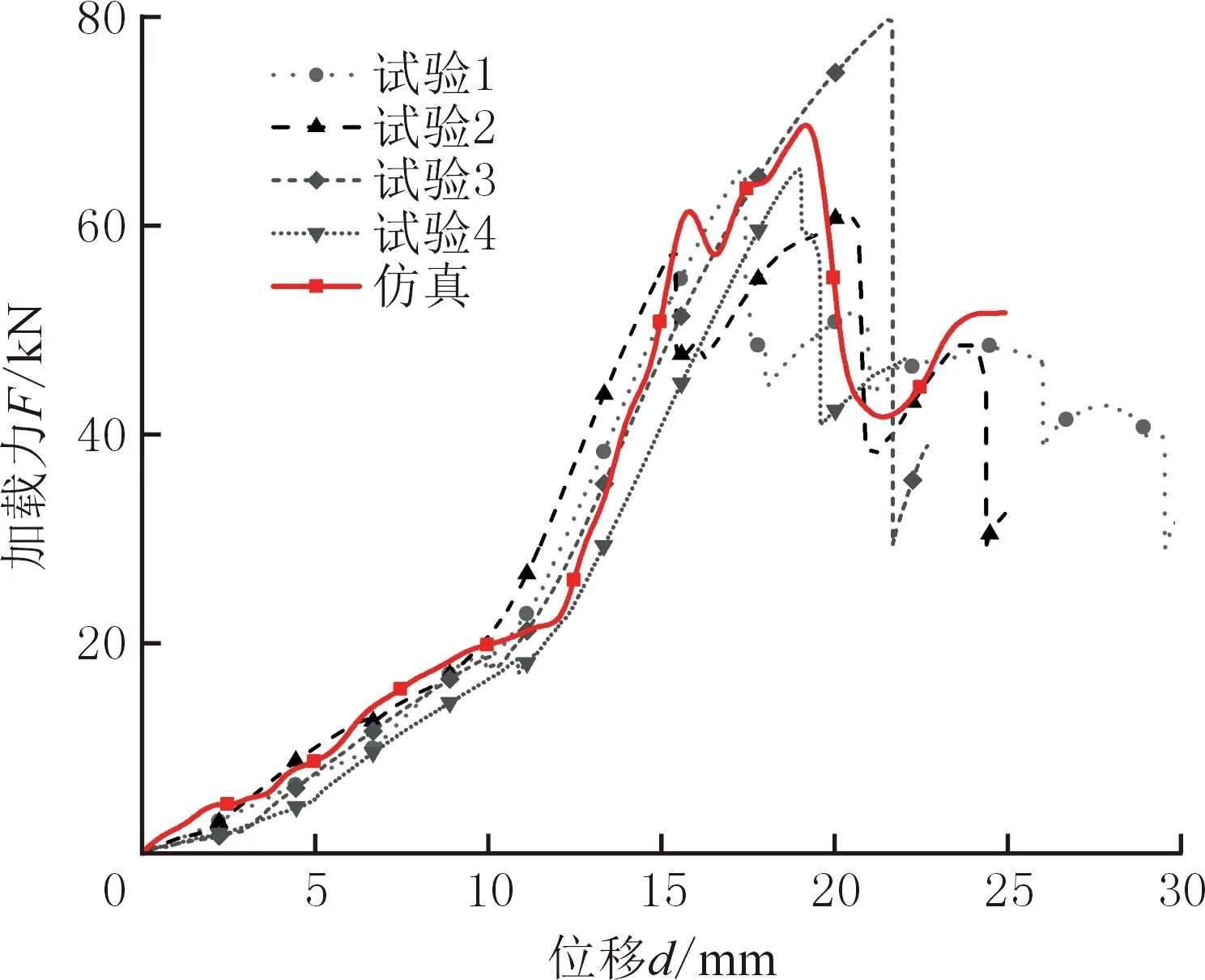
图14 轮辋压溃仿真与试验的加载力-位移曲线Fig.14 Force-displacement curves of simulation and test in wheel rim collapse

3.3 动态落锤冲击的有限元模拟

利用准静态压缩模拟获得了更为合理的六面体单元轮毂断裂失效建模方法，将该方法应用于轮毂动态落锤冲击的仿真中，失效位置集中在与落锤压头接触的区域以及与半轴连接的轮毂中心，动态落锤冲击试验中轮毂断裂位置和变形模式基本与轮毂平板压溃试验中的轮毂断裂位置和变形模式接近，且试验结果与仿真结果具有较好的一致性。图15所示为落锤冲击的仿真和试验加速度历程曲线对比。经过缩放修正后，加速度曲线的吻合度较高，曲线相关性可达88%，表明仿真可以准确地模拟轮毂的碰撞失效过程。上述研究结果表明，基于CrachFEM失效准则开发的材料模型可以有效地预测轮毂在冲击载荷作用下的断裂行为。

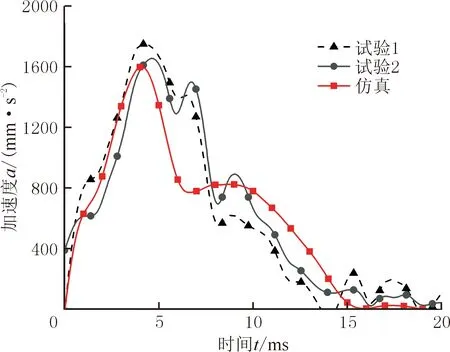
图15 落锤冲击仿真与试验的加速度-时间曲线Fig.15 Acceleration-time curves of simulation and testin drop-weight impact

4 结论

(1)针对小偏置碰仿真中轮毂断裂模拟的难题，通过材料力学试验建立了基于CrachFEM韧性失效准则的AlSi7材料卡片，可同时描述材料的弹塑性、断裂失效特性和应变率特性。

(2)进行了轮毂的准静态、动态试验与有限元仿真结果对比，结果表明，CrachFEM材料模型可以准确地模拟铸铝轮毂在碰撞载荷冲击下的断裂行为，仿真结果与试验结果具有良好的一致性。

(3)为进一步准确地模拟轮毂的断裂失效，采用六面体单元进行网格划分。相比于二阶四面体单元，虽然六面体单元建模工作偏于复杂，但能显著提高碰撞接触区域单元的失效模拟精度，并减少计算耗时。

(4)铸造缩孔分布与轮毂结构特征、加工工艺有关，轮毂中心的韧性明显低于轮辋的韧性，轮毂中心的断裂特性可通过缩放系数(设置缩放系数为0.55)进行调整，要求有限元建模时在轮毂中心和轮辋独立定义带失效参数的材料模型，可以更加可靠地模拟轮毂的碰撞断裂现象。