基于改进IGG3权函数距离误差模型的工业机器人标定
张恩政 唐宁敏 陈 刚 刘翠苹
1.浙江理工大学精密测量实验室,杭州,3100182.杭州市质量技术监督检测院机器人实验室,杭州,3100193.杭州新松机器人自动化有限公司,杭州,311225
0 引言
工业机器人具有重复性定位精度较高、稳定可靠、能在高危环境下作业等优势,在传统制造业、特别是劳动密集型产业的转型升级中发挥着重要作用[1]。工业机器人具有的较高重复性定位精度基本可满足空间位置点的定位精度需求,但难以满足目前一些领域对高绝对定位精度的要求[2]。机器人长时间的使用以及磨损也会导致绝对定位精度的下降[3-4],因此,对工业机器人进行适时标定以确保其处于较高的绝对定位工作精度是机器人应用中的重要环节。
工业机器人的标定过程大致包括建模、测量、辨识和补偿四个步骤[5],其中模型参数辨识是标定过程的关键步骤。为提高工业机器人运动学模型参数的准确度,国内外已开展了机器人标定方法的大量相关研究,基本可分为基于位置误差模型的标定和基于距离误差模型的标定。
基于位置误差模型的标定是目前常用的方法,JIANG等[6]提出了基于卡尔曼和粒子滤波的机器人位置误差模型运动学标定方法;房立金等[7]提出了基于量子粒子群优化算法的几何参数标定方法,利用优化获得的参数修正量更新运动学模型;温秀兰等[8]提出了基于改进粒子群算法的机器人几何参数标定方法,并进一步提高了机器人的标定精度。MESSAY等[9]提出使用结合模拟退火和信任区域的新型混合算法进行参数辨识;张强等[10]针对机器人手眼标定过程中存在的测量粗差影响标定精度的问题,提出了一种误差分布估计的机器人手眼标定算法,在一定程度上提高了机器人手眼标定精度;向民志等[11]提出基于抗差估计的工业机器人位置误差标定算法,相较于传统最小二乘法拟合算法,所提算法在进行机器人标定时的精度更高且鲁棒性更强;KLIMCHIK等[12]考虑了粗差对机器人末端定位的影响,增加了一个归一化因子,但对粗差的处理较为粗略。
上述基于位置误差模型的标定方法存在机器人坐标系与测量设备坐标系转换时的转换误差对标定精度产生影响的共性问题,为了解决该问题,基于距离误差模型的标定方法被提出并已应用到机器人标定中。姚兴田等[13]提出将距离误差模型应用于服务机器人运动学标定方法中,提高了服务机器人的绝对定位精度;李定坤[14]利用基于距离误差模型的最小二乘算法辨识运动学参数,通过最小化残差的平方和来求取数据的最佳匹配值,但当标定采样点中存在测量粗差值时,则会继续将粗差值代入计算,这部分粗差值对残差平方和的影响比其他观测值要大得多,从而会使得估计量受到严重影响。由此可知,基于距离误差模型的标定方法可避免出现坐标系转换引入附加误差的问题,但标定过程中测量数据的粗差仍然会对标定结果产生较大影响。
针对基于距离误差模型的机器人标定方法中测量粗差数据会对标定精度产生影响的问题,本文提出了一种基于改进IGG3权函数距离误差模型的工业机器人标定方法,将改进的IGG3权函数最小二乘辨识算法应用于工业机器人距离误差的标定中,从消除坐标系转换误差和减小数据粗差影响的角度提高工业机器人的标定精度。
1 机器人距离误差模型建立
1.1 运动学模型
本文以SR4C型工业机器人为研究对象进行Denavit-Hartenberg(D-H)运动学建模,该机器人为六自由度串联机械臂,具体包括腰部回转、大臂俯仰、小臂俯仰、手腕回转、手腕俯仰、手腕侧摆六个自由度。为了建立D-H模型,首先要对机器人的每一个关节建立坐标系统,如图1所示,其中,机器人的基坐标系{W0}(O0x0y0z0)和第一关节坐标系{W1}(O1x1y1z1)重合。
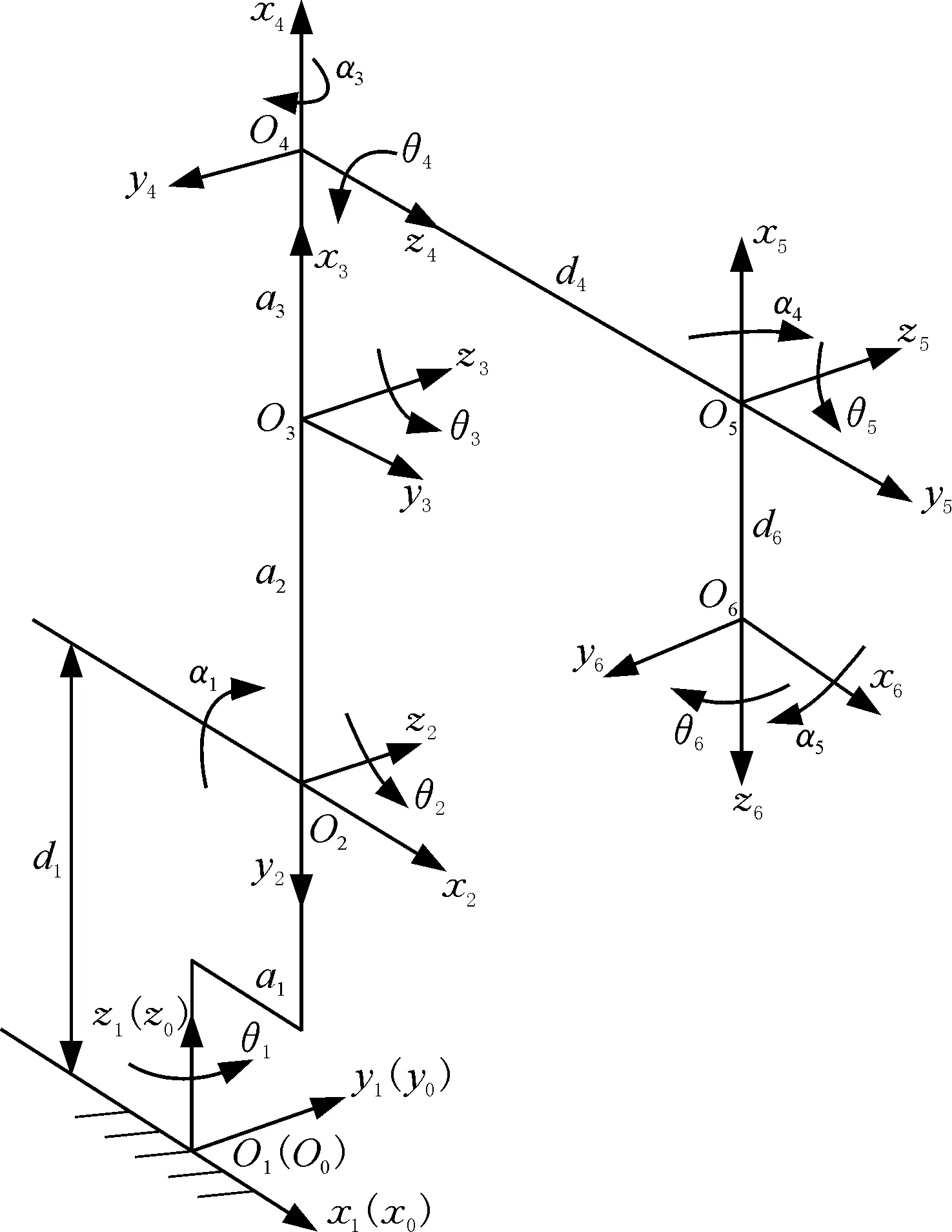
图1 SR4C型工业机器人关节坐标系Fig.1 SR4C industrial robot joint coordinate system
如图1所示,机器人相邻两个关节间坐标系的理论转换矩阵可表示为
(1)
式中,i(i=1,2,…,6)为关节编号;ai为连杆长度;αi为连杆扭转角;di为连杆偏移量;θi为关节转角。
基于式(1)所示的关节坐标系转换矩阵,将各关节转换矩阵依次相乘,可以得到机器人末端坐标系{W6}(O6x6y6z6)相对于基坐标系{W0}(O0x0y0z0)的理论变换矩阵为
(2)
式中,(Px,Py,Pz)为机器人末端坐标系的原点在基坐标系下的位置坐标;(nx,ny,nz)T、(ox,oy,oz)T、(ax,ay,az)T分别为机器人末端坐标系x、y、z轴相对于基坐标系的方向余弦。
1.2 位置误差模型
(3)
对式(1)进行全微分,并代入式(3)可得
(4)
式中,di为位置误差向量;δi为姿态误差向量; Δai为实际和理论连杆长度之间的偏差;Δαi为实际和理论连杆扭转角之间的偏差;Δdi为实际和理论连杆偏移量之间的偏差;Δθi为实际和理论关节转角之间的偏差。
将式(3)所示的相邻关节坐标系的实际变换矩阵依次相乘,可以得到机器人末端坐标系相对于基坐标系的实际位姿矩阵为
(5)
式中,TN为机器人末端坐标系相对于基坐标系的理论矩阵;TD为机器人末端坐标系相对于基坐标系的位姿误差矩阵。
令关节i到关节6的坐标系转换矩阵依次相乘为Ui,其表达式如下:
(6)
式中,ni、oi、ai为姿态矩阵的3个3×1的列向量;Pi为3×1的位置向量。
由式(5)可得机器人末端坐标系相对于基坐标系的位姿误差矩阵为
(7)
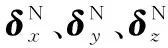
由式(7)可得到机器人的位置误差模型为
(8)
式中,J为机器人的雅可比矩阵;Δq为待辨识的实际D-H参数与理论D-H参数之间的偏差;O1×3为1×3的零向量。
1.3 距离误差模型
以位置误差模型为基础可以推导出机器人距离误差模型,距离误差向量关系如图2所示。设机器人指令轨迹上选取的两点为j点和j+1点,对应两点之间的理论距离用sO表示。设指令轨迹上选取的两点对应实际轨迹上的j′点和j′+1点,两点之间的实际距离用sR表示。则指令轨迹两点之间距离与实际轨迹两点之间距离的差值可以表示为
Δs=sO-sR
(9)
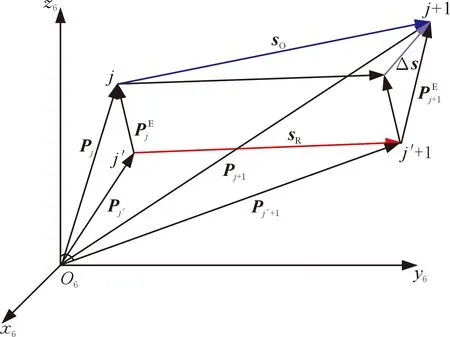
图2 距离误差向量关系图Fig.2 Distance error vector diagram
由图2所示的向量关系可得[15]
sOΔs≈|sO||Δs|
(10)
根据式(9)和位置误差模型(式(8))可得到机器人的距离误差模型为
(11)
式中,(xO(j+1),yO(j+1),zO(j+1))、(xO(j),yO(j),zO(j))分别为j+1点和j点在指令轨迹上的坐标;ΔxO(j+1)、ΔyO(j+1)、ΔzO(j+1)分别为j+1点在x、y、z方向的位置误差;ΔxO(j)、ΔyO(j)、ΔzO(j)分别为j点在x、y、z方向的位置误差。
在上述基本距离误差模型中,空间随机点之间的距离是不定值,为减少因两点间距离误差值差异过大而带来的计算舍入误差,本文研究给出基于球面选点的等距离误差模型,以简化模型和计算。在等距离误差模型中,固定空间中一点为球心,将球心坐标设为(xc,yc,zc),其余点处于以该点为球心、R为半径的球体包络面上,如图3所示。由式(11)并结合式(8)可得等距离误差模型为
Δs=
(12)
式中,Jj为j点对应的雅可比矩阵;Jc为球心对应的雅可比矩阵。
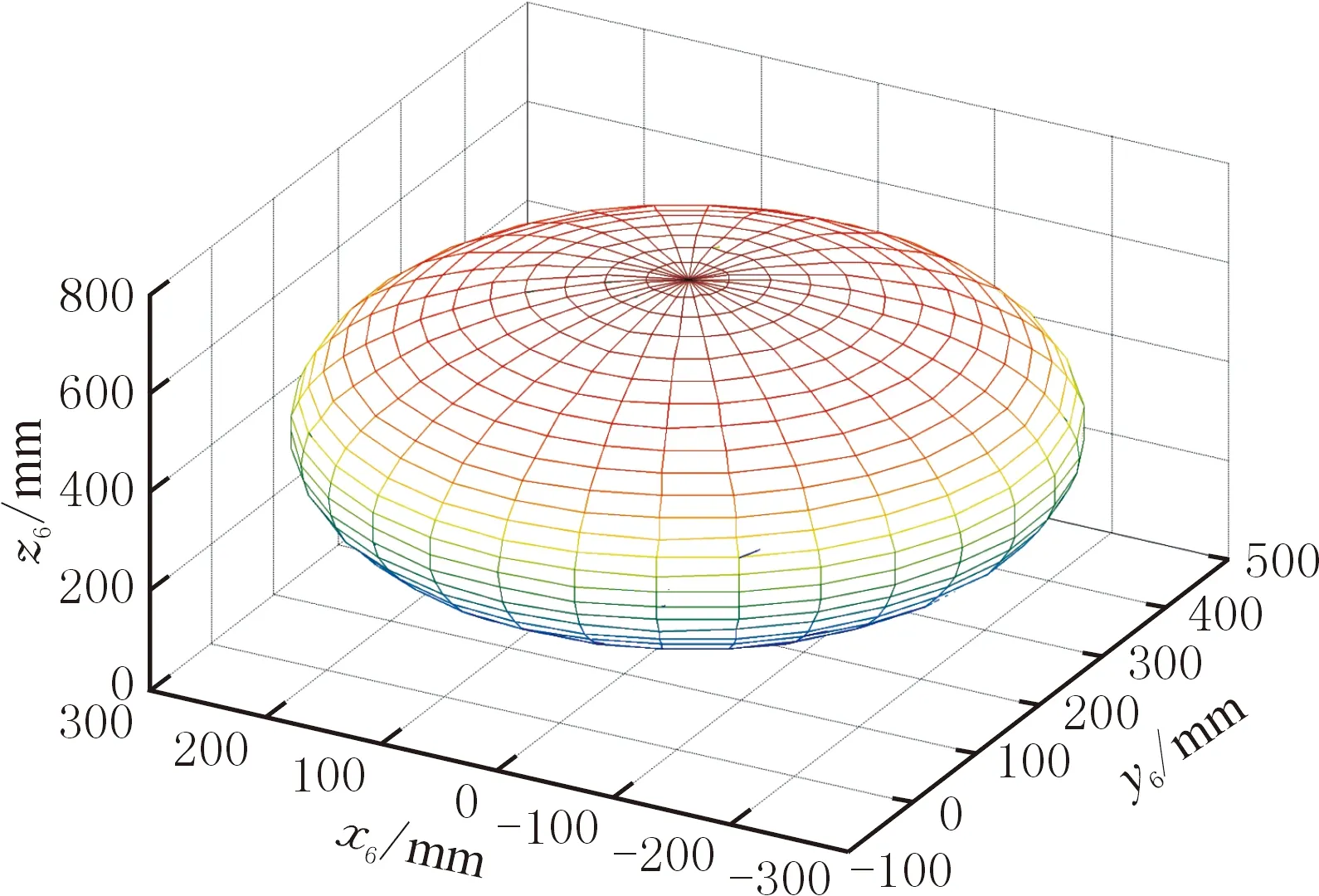
图3 等距误差模型采样球面Fig.3 Isometric error model sampling sphere
当已知机器人位置误差时,可由式(8)计算得出当前绝对定位误差对应的D-H运动学参数误差Δq。将所得到的Δq代入式(12)所示的等距离误差模型中即可计算出对应的距离误差,反之也可由距离误差反推得到位置误差,因此,机器人的距离误差和绝对定位误差有一一对应的关系,距离精度可以作为绝对定位精度的度量标准之一。
2 改进IGG3权函数的最小二乘辨识算法
将式(12)中除Δq以外的表达式用矩阵H来代替进行化简,可得
Δs=HΔq
(13)
利用最小二乘法进行计算可得
Δq=(HTH)-1HTΔs
(14)
当观测数据呈正态分布时,采用最小二乘法可以准确地求取Δq,但当观测值中存在远离数据群体的观测值(即测量粗差值)时,这些粗差值对残差平方和的影响要比其他观测值对残差平方和的影响大得多,从而会导致估计量受到严重影响,因此考虑使用抗差估计法来排除粗差值的影响。
极大似然估计法是抗差估计的常用方法,其原理为:利用已知的样本结果反推最大概率导致这样结果的参数值,得出极大似然估计量,可以尽可能地削弱粗差值对结果的影响。此处的样本结果为Δs=(Δs1,Δs2,…,ΔsN),参数值为Δq。首先建立极大似然函数:
l(Δq)=p(Δs1,Δs2,…,ΔsN|Δq)=
(15)
式中,p(·)为样本结果Δs的概率密度函数;N为采样点个数。
根据极大似然原理,固定样本观测值Δs1,Δs2,…,ΔsN,挑选参数Δq使得
max(p(Δs1,Δs2,…,ΔsN|Δq)
(16)

对式(16)等号两边取对数并整理可得
(17)
令ρ(Δsj,Δq)代替-ln(p(Δsj,Δq)),可得
(18)
计算中使用改正数vj(j=1,2,…,N)来衡量粗差大小,vj可表示为
vj=HjhΔqh-Δsj
(19)
其中,Hjh为矩阵H中第j行第h列元素,Δqh为Δq中第h个参数。则可将式(18)中ρ(Δsj,Δq)写成ρ(vj),可得
(20)
为求解出式(20)的极值,对其进行求导,可得
(21)
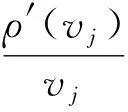
(22)
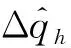
(23)
v=(v1,v2,…,vN)T
对式(23)变换可得
(24)
其中,P(v)为权函数矩阵,且为对角阵,具体形式为P(v)=diag(p1,p2,…,pN)。
将式(24)与标准最小二乘法得到的模型参数误差计算公式(式(14))相比可知,基于抗差估计的最小二乘法与标准最小二乘法之间的差别为增加了一个权函数矩阵P(v),即在计算最小二乘残差平方和时给予每个残差不同的权值以控制其在总体计算中所占的比重。
基于抗差估计的最小二乘法权函数矩阵通常采用IGG3权函数,IGG3权函数的表达式如下:
(25)

IGG3权函数的调和系数k0、k1根据正态分布标准差面积占总面积比值选取,正态分布中±1.5个标准差范围内的面积占总面积的86.6%,该范围内的观测值应尽量保留;正态分布中±2.5个标准差范围内的面积占总面积的98.7%,该范围外的观测值远离样本群体,应尽量剔除。综上,k0常取值1.5,k1常取值2.5。
IGG3权函数的一阶导数在k0处不连续,导致函数在k0处不平滑,则k0附近的可利用信息在抗差估计中得不到充分利用[16],因此本文选用改进的IGG3权函数将残差数据分为4段,以避开不可导的点,改进的IGG3权函数可表示为
(26)
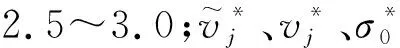
由于式(14)中(HTPH)-1矩阵为超定病态阵,外部微小扰动会影响参数值的结果,因此对式(24)进行岭估计,其表达式如下:
(27)
其中,I为单位矩阵;α为岭估计方法系数,取经验值0.01,用来避免出现(HTPH)-1矩阵的条件数过多且因(HTPH)-1矩阵接近病态矩阵而对微小扰动十分敏感的情况。
基于上述改进IGG3权函数距离误差模型的机器人标定算法的标定流程如图4所示,其中,qk为当前迭代过程的运动学参数,qk+1为后一次迭代过程的运动学参数。
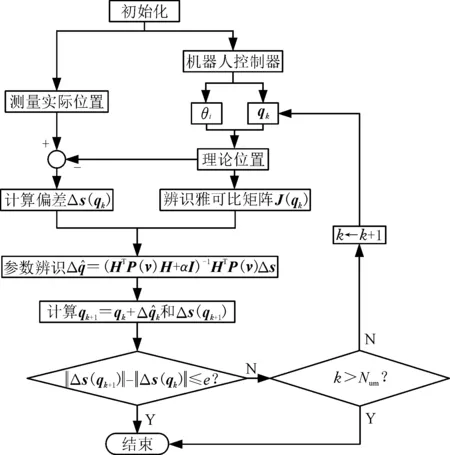
图4 距离误差标定算法流程图Fig.4 Flow chart of distance error calibration algorithm
算法的主要流程如下:将测量的实际位置值和机器人理论位置值及理论参数作为输入,计算出距离偏差Δs,同时根据机器人距离误差模型计算出对应的雅可比矩阵J,将二者代入基于改进IGG3权函数的最小二乘距离误差辨识算法中进行参数辨识并迭代,根据设定的距离误差阈值e和最大迭代次数Num进行判断,当其中之一的条件满足时便停止迭代,并输出辨识结果,从而完成模型参数误差的辨识。
3 实验验证与分析
3.1 实验平台的搭建
为分析与验证所提出基于改进IGG3权函数距离误差模型的工业机器人标定方法的有效性和可行性,构建了图5所示的实验系统,主要包括Leica AT960激光跟踪仪、SR4C型六自由度机器人及其配套装置等。激光跟踪仪的测量精度为±10 μm,系统分辨力为0.1 μm,最大跟踪速度为6 m/s;机器人工作范围为0~672.8 mm,机器人的理论D-H参数将作为辨识算法的输入代入计算,具体参数如表1所示。

图5 实验系统Fig.5 Experimental system
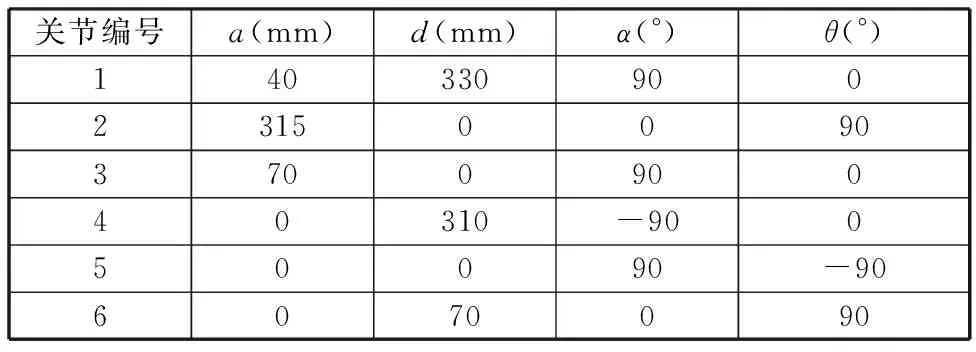
表1 机器人理论D-H参数表
3.2 辨识算法对比实验
本文开展了辨识算法的对比实验来验证基于改进IGG3权函数距离误差模型的机器人标定算法的有效性和可行性,具体步骤如下。
(1)在实验前先将激光跟踪仪开启并预热20 min,然后确定球心、球体半径并规划采样点,如图6所示。利用MATLAB中sphere函数将所生成的球面划分成30×30个小网格,以便采样点的选取,从已划分的球面网格中均匀地选取50个采样点。
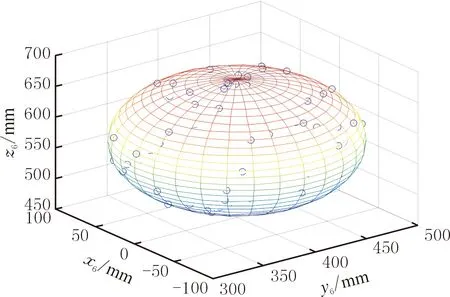
图6 采样点规划Fig.6 Sampling point planning
(2)规划好50个采样点后控制机器人依次进行运动,利用激光跟踪仪对采样点进行测量。首先进行轨迹规划,在机器人当前位置到第一个指令点之间采取关节空间梯形速度规划;50个采样点之间进行笛卡儿空间直线轨迹规划,再通过机器人逆解算法及最小路径算法将机器人笛卡儿空间坐标值转换成关节坐标值再转换成编码值下发给控制器,每个采样点位之间设置2 s停顿,以供激光跟踪仪进行数据采集。
(3)将靶球固定于末端执行器,在机器人作业的同时,通过跟踪仪测量得到50个位置坐标。
(4)将测量得到的50组测量值和获取的50组关节坐标值以及表1中的理论参数代入辨识算法中进行辨识,并得到一组新的D-H参数。
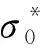
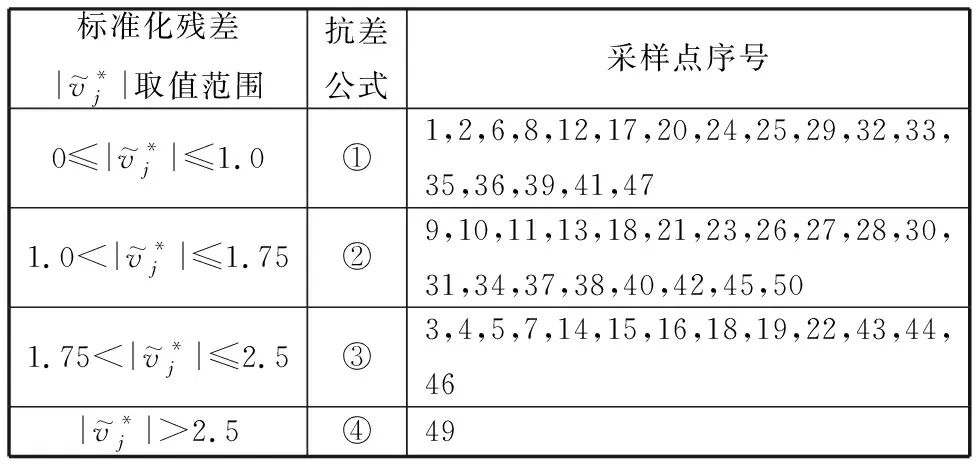
表2 抗差数据处理情况
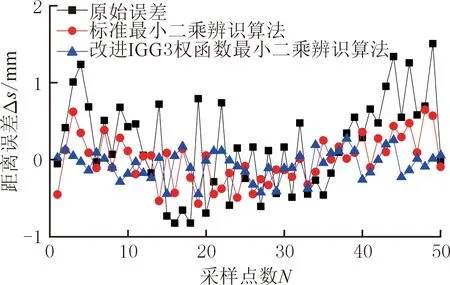
图7 辨识算法比对实验结果Fig.7 Comparison experimental results of identification algorithm
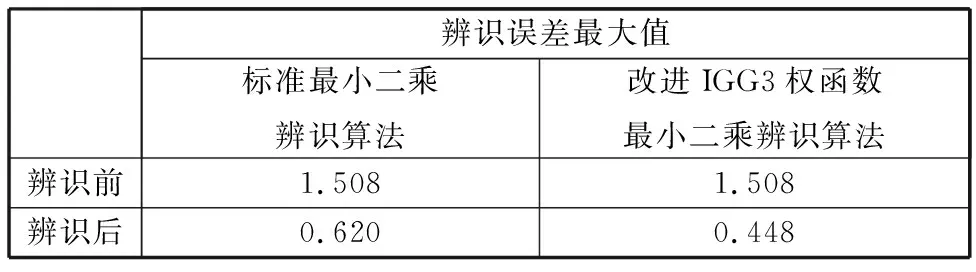
表3 标准最小二乘与改进IGG3权函数最小二乘辨识实验结果
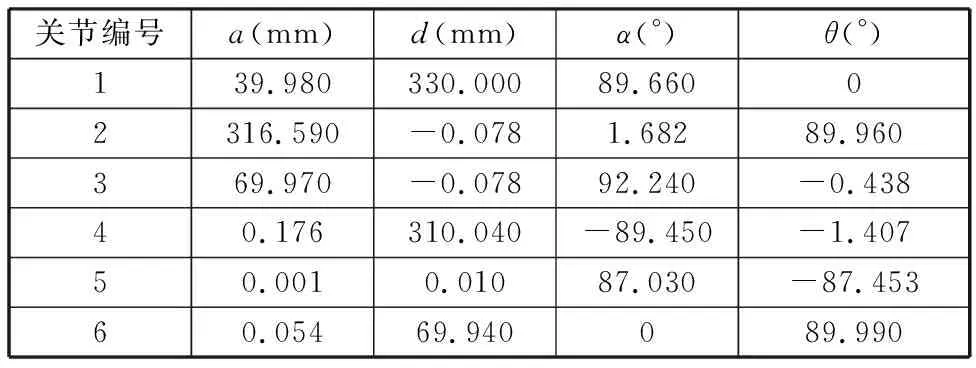
表4 改进IGG3权函数辨识D-H参数表
对比实验结果表明:使用标准最小二乘辨识算法和改进IGG3权函数最小二乘辨识算法均可显著地减小距离误差值,且与标准最小二乘辨识算法相比,利用本文提出的改进IGG3权函数最小二乘辨识算法能更加有效地减小距离误差值。
3.3 补偿实验
为验证经运动学参数误差补偿后的机器人定位精度,将辨识出的D-H参数表覆盖原始理论的D-H参数表,重新对50个目标点进行误差补偿。机器人依次运行50个目标点,同时利用激光跟踪仪进行测量,得到测量坐标点。根据机器人距离误差模型公式,计算50个点到球心点的距离与标准半径之间的差值,得到补偿后的距离误差值。选取半径R=100 mm的球面采点,其补偿前后机器人的距离误差如图8和表5所示。
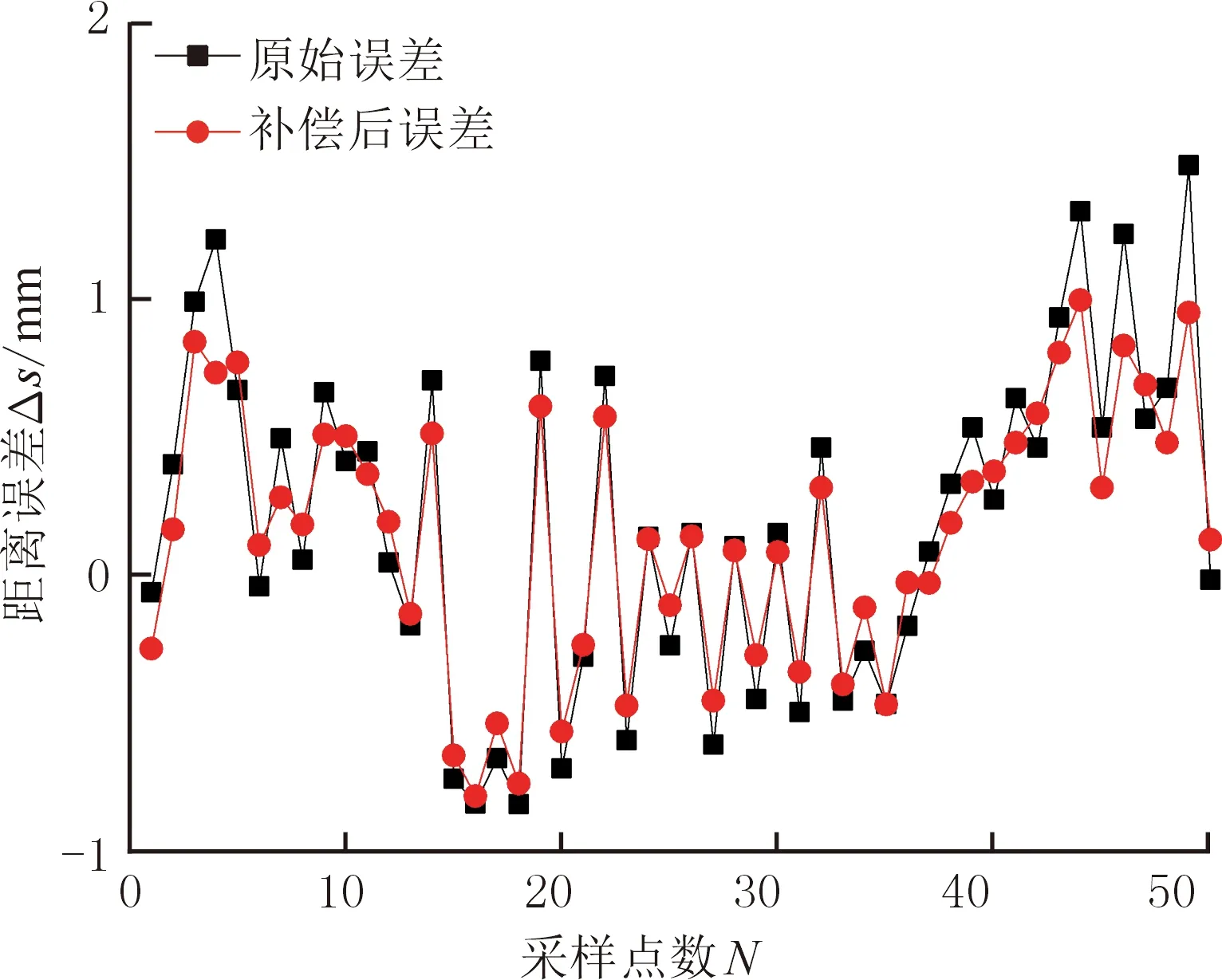
图8 补偿前后的实验结果Fig.8 Experimental results before and after compensation

表5 距离误差补偿前后实验结果
补偿实验结果表明:在R=100 mm的距离误差补偿实验中,补偿后的距离误差值比补偿前的距离误差值减小了32.69%。
本次实验研究对象为新松SR4C型工业机器人,是提供底层开发接口进行运动算法控制的实验样机,与商业用的机器人相比在正逆解算法精确度、轨迹规划算法中速度平稳性能方面仍存在不足,除运动学参数误差导致的末端位置误差之外,这两方面因素也会极大影响机器人的末端定位精度。实验结果表明,利用所提出的基于改进IGG3权函数距离误差模型的辨识补偿方法可减小距离误差值,从而可提高工业机器人的精度。
4 结语
本文针对基于距离误差模型的工业机器人标定方法在实验过程中存在的粗差问题,提出了将改进的IGG3权函数最小二乘辨识算法用于距离误差工业机器人标定中,以进一步提高工业机器人的标定精度。开展了改进IGG3权函数的机器人标定算法研究,基于SR4C型工业机器人构建了算法验证和补偿实验系统,并开展了实验研究。实验结果表明:标定后的精度比标定前提高了32.69%,从而验证了所提方法的可行性。本文研究的基于改进IGG3权函数距离误差模型的工业机器人标定方法可用于工业机器人标定和校准领域,可为工业机器人定位精度的提高提供一定的理论和方法参考。

