基于有限元模拟的Ti6Al4V铣削过程参数多目标优化

黎宇嘉 黄 兵 鲁 娟，2 钟奇憬 陈超逸 廖小平 马俊燕

1.广西大学广西制造系统及先进制造技术重点实验室，南宁，5300042.北部湾大学机械与船舶海洋工程学院，钦州，535011

0 引言

铣削工艺已广泛用于金属加工中，其工艺参数的设定影响着加工效益[1]。在加工效益指标中，表面粗糙度影响着产品的质量与制造成本。世界工业化对环境产生了不可忽视的影响，环境意识制造(environmentally conscious manufacturing，ECM)这一概念被提出来，主要用于解决加工过程中的能耗问题。针对以表面粗糙度或能耗为目标的优化，相关研究者已作了大量的探索。尚宝平等[2]构建了基于近似模型的铣削工艺参数可靠性优化模型，发现优化后的铣削参数成功降低了此加工过程中的表面粗糙度；JANG等[3]根据物理试验数据建立了特定的切削能量预测模型，并对模型进行优化获得了切削能量最小的切削条件；AHMED等[4]结合田口L9正交试验和多目标遗传算法，研究了铣削四要素对质量特性的影响，确定了表面粗糙度和能耗的最优控制参数组合。采用设计物理试验的方法获得优化所需的数据会消耗大量的时间以及花费高昂的设备材料成本，这使得优化数据的获取变得困难。

有限元模拟是一种可以通过设计较易理解的成形参数来达到简化成形过程效果的参数化模型分析方法，不仅能节省试验中材料的成本，也可缩短工艺参数选择的周期。为了降低物理试验的成本，THEPSONTHI等[5]建立了铣削的三维有限元模型，研究了磨刃半径的增大对微端铣削加工性能的影响，仿真与实验结果较为吻合；SATYANARAYANA等[6]利用有限元仿真软件Deform-3D对Ti6Al4V钛合金的加工过程进行了仿真分析，研究了铣削参数对铣削力和温度的影响，发现仿真数据与实际数据的误差在允许范围内。但利用有限元模型作为优化方法的适应度模型会导致每一次寻优迭代都要消耗大量时间，从而会降低优化的效率。使用高保真度的高效代理模型可以解决上述问题。

近年来，辅助代理进化算法在解决多目标优化问题上有突出的表现。高斯过程代理模型已经被证明在优化多决策变量问题上具有优异的性能，TIAN等[7]将高斯过程代理模型与粒子群优化(particle swarm optimization，PSO)算法相结合，解决了高维决策变量的优化问题。

为使切削加工过程满足ECM要求的同时降低数据获取成本，本文针对质量指标(表面粗糙度)和ECM指标(能耗)，采用有限元仿真软件Deform-3D模拟Ti6Al4V的铣削过程，以获取加工参数与加工目标的数据；采用人工蜂群(artificial bee colony，ABC)算法优化的高斯过程回归(Gaussian process regression，GPR)方法构建有限元仿真的代理模型，并采用多目标粒子群优化 (multi-objective particle swarm optimization，MOPSO) 算法获取最优加工目标的加工参数。

1 基于Deform-3D仿真的数据获取

Deform-3D[8]获取决策变量对应的能耗与表面粗糙度的操作主要包括三步：前处理、模拟过程、后处理。前处理的主要考虑有：本构模型、刀-屑摩擦模型和刀具磨损模型的建立，网格划分，切屑分离准则的设置，铣削参数的选择。前处理的参数经过Deform-3D的求解器转换得到工件表面节点坐标和铣削力。表面粗糙度和能耗可由工件表面节点坐标和铣削力经过相应的公式转化得到。图1为仿真流程图。

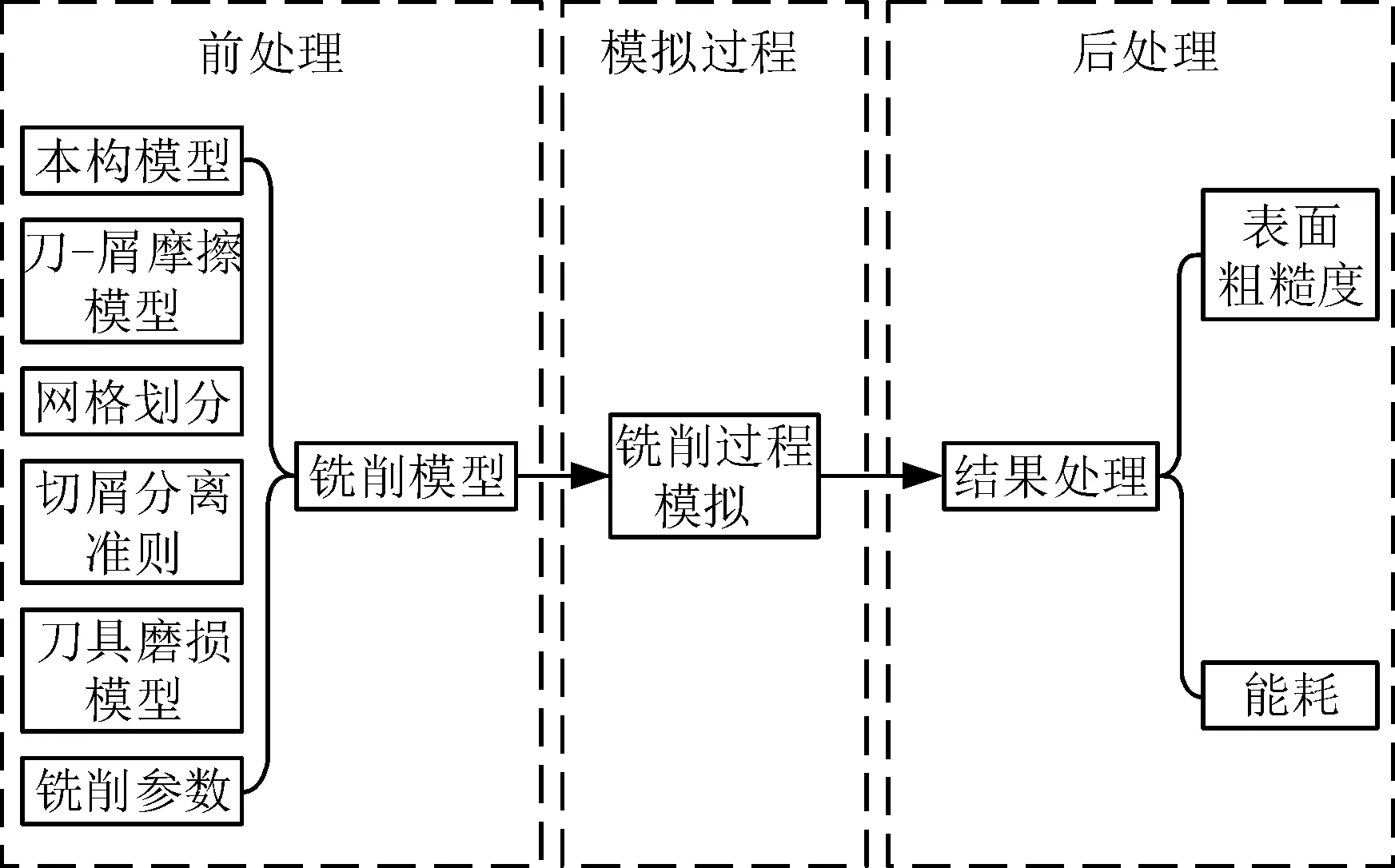
图1 Deform-3D仿真基本流程图Fig.1 Basic flow chart of Deform-3D simulation

1.1 Deform-3D前处理中的关键技术

本文用UG软件完成工件、刀具几何模型的构建，以.stl形式导入Deform-3D软件中，如图2所示，其中刀具为φ14 mm的两齿铣刀。

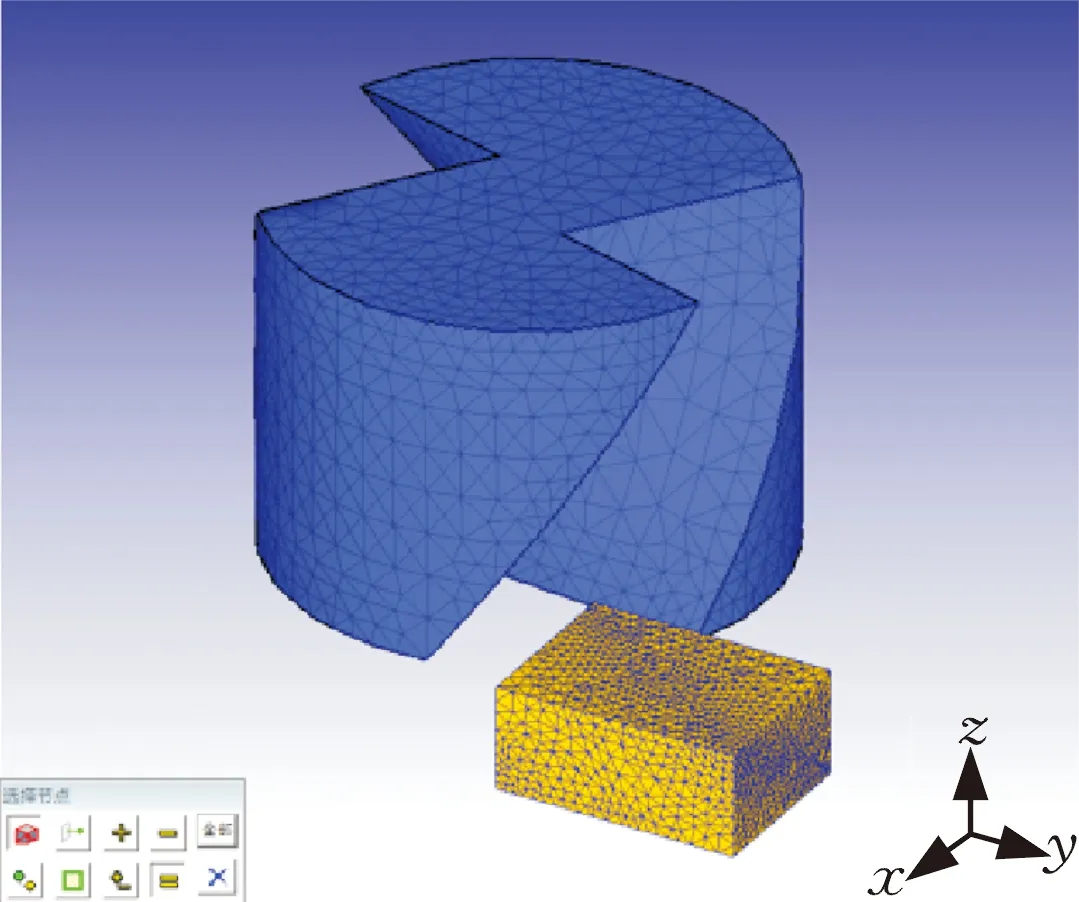
图2 导入的工件、刀具几何模型Fig.2 Imported workpiece and tool geometric model

关键项的设置会影响仿真结果与实际结果的偏差，本文主要考虑的因素如表1所示。其中工件和刀具网格数目根据仿真调试得出，其他模型与参数根据相应的文献选择。

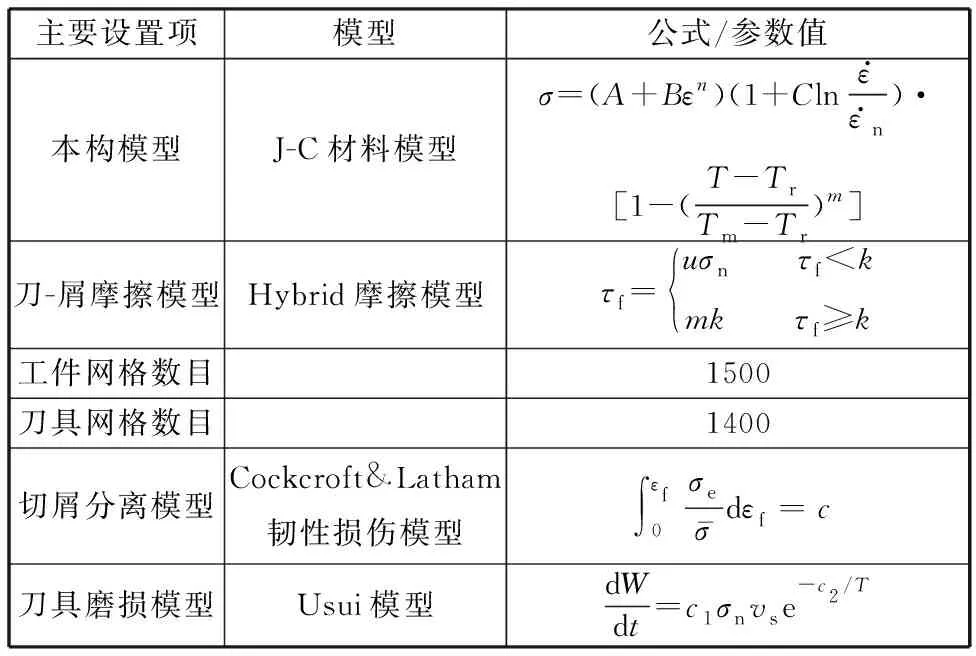
表1 关键项的设置[9-10]

本文将铣削加工可控因素中的主轴转速、轴向切深、径向切深和进给速度作为仿真的输入，探索输入与表面粗糙度、能耗两个目标之间的关系，为此设计了四因素五水平的正交试验来进行仿真分析，各切削参数的取值如表2所示。

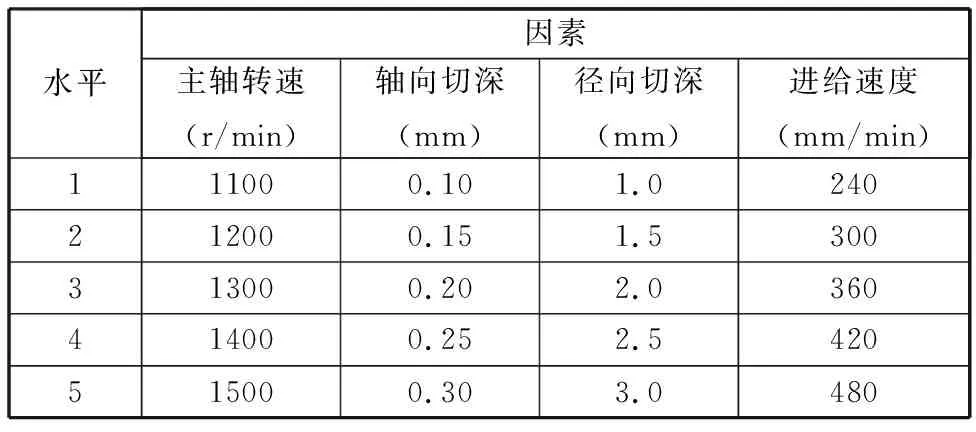
表2 正交试验切削参数

1.2 Deform-3D的后处理分析

经过前处理与铣削仿真模拟，得到了仿真铣削加工中切削接触点的坐标(x，y，z)、仿真得到的主切削力Fsim和铣削过程中所需的时间t。为了得到相应的表面粗糙度和能耗，对仿真数据进行相应的后处理。

1.2.1表面粗糙度的计算

本文选取采样长度l下内轮廓偏距算术平均值的绝对值Ra作为衡量表面粗糙度的指标，其计算表达式如下：

(1)

仿真结束后，在工件加工面的进给方向上选取3个不同位置，取径向切深为采样范围，采集该范围下的z方向坐标，依据式(1)计算Ra，最终取3个位置处表面粗糙度的平均值作为最终的表面粗糙度值。

1.2.2能耗的计算

在加工过程中，对环境影响最大的因素是能耗[11]，因此，本文以单位体积内消耗的能量为ECM指标展开研究，其计算式为

(2)

Vtotal=aeapL

式中，ESEC为单位体积能耗；Ecut为仿真参数下铣削所对应的能耗量；Vtotal为仿真参数下工件去除的体积；ae为径向切深；ap为轴向切深；L为铣削长度，取L=15 mm；vc为进给速度；n为主轴转速；D为刀具直径。

2 有限元仿真与物理试验的对比验证

2.1 物理试验平台的搭建

为验证有限元仿真的结果，选取与仿真相同的参数在VDL-600A数控机床上进行铣削物理试验，现场试验平台如图3所示。

图3 试验平台Fig.3 Test platform

表面粗糙度与铣削力分别通过三丰SJ310表面粗糙度仪线下测量和JR-YDCL-Ⅲ05B测力仪在线测量获得。由于三向测力仪在z方向上的切削力远大于其他方向的切削力，因此将其作为主切削力(即铣削过程中的铣削力)。刀具的基本信息如下：刀具尺寸φ14 mm×120 mm，刀尖半径0.8 mm，齿数为2，涂层为TiAlN。试验工件的材料采用与仿真时一样的Ti6Al4V材料，加工平面的尺寸为80 mm×15 mm，其中刀具进给方向的长度为15 mm。

2.2 物理试验与有限元仿真的对比

在进行了25组仿真与物理试验铣削加工的正交试验后，将有限元仿真得到的z方向坐标值代入式(1)得到表面粗糙度值，而物理试验的表面粗糙度值通过测量得到，将仿真和物理试验得到的主切削力分别代入式(2)可得到对应的能耗。正交试验方案和结果如表3所示，其中因素A为主轴转速n(r/min)，B为轴向切深ap(mm)，C为径向切深ae(mm)，D为进给速度vc(mm/min)。

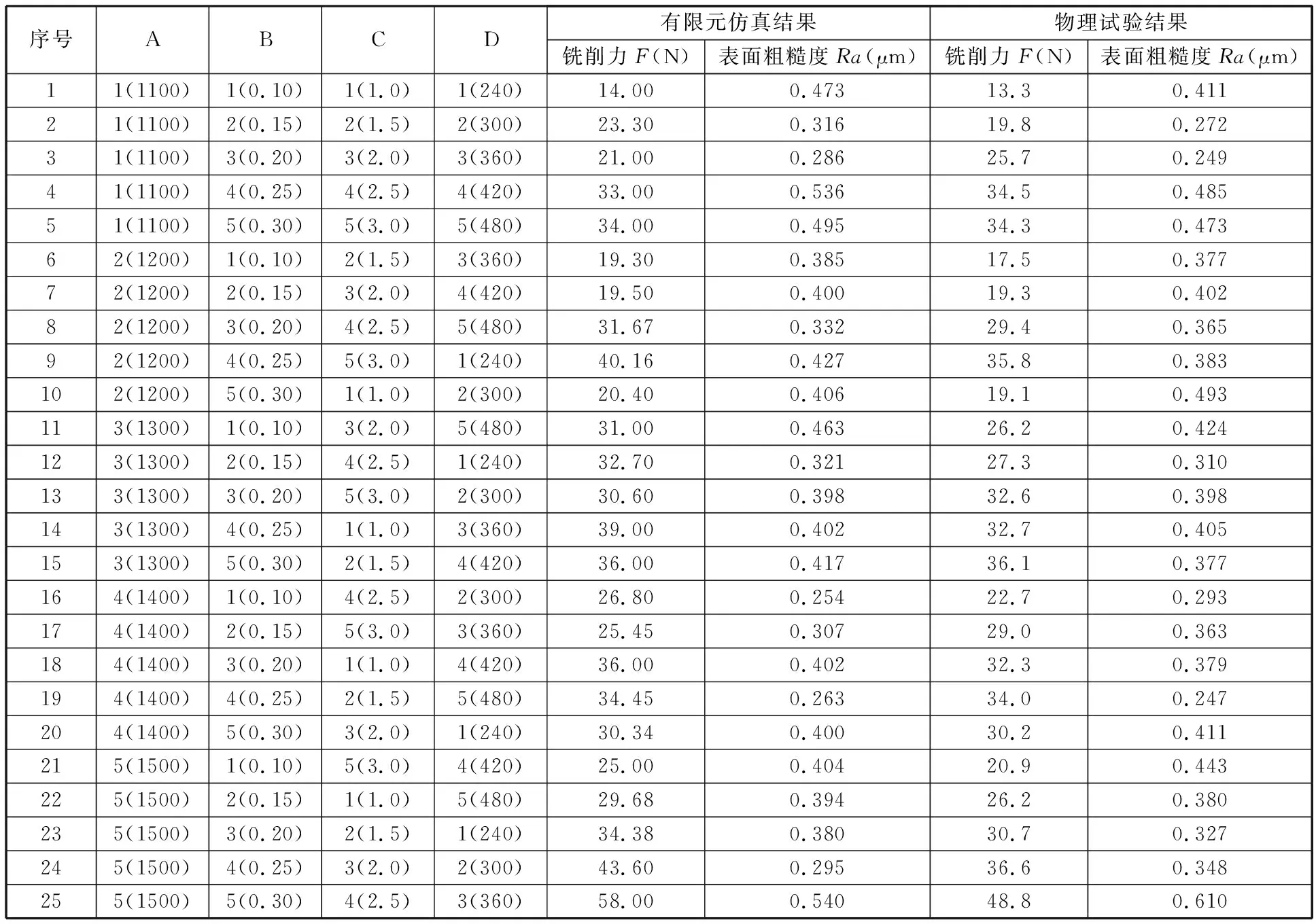
表3 正交试验设计方案以及仿真和物理试验结果

由式(2)可知，在同一组铣削的有限元仿真和物理试验中，当vc、t和Vtotal一定时，能耗仅与主切削力Fsim有关，因此本文用主切削力(即铣削力)的变化来反映能耗的偏差程度。为了验证仿真的有效性，将仿真和物理试验得到的表面粗糙度和铣削力分别进行对比。由图4和图5可知，有限元仿真结果与物理试验结果有相同的变化趋势，表面粗糙度与铣削力误差的均值分别为9.11%和10.50%，从而验证了第1节中有限元模型的有效性。

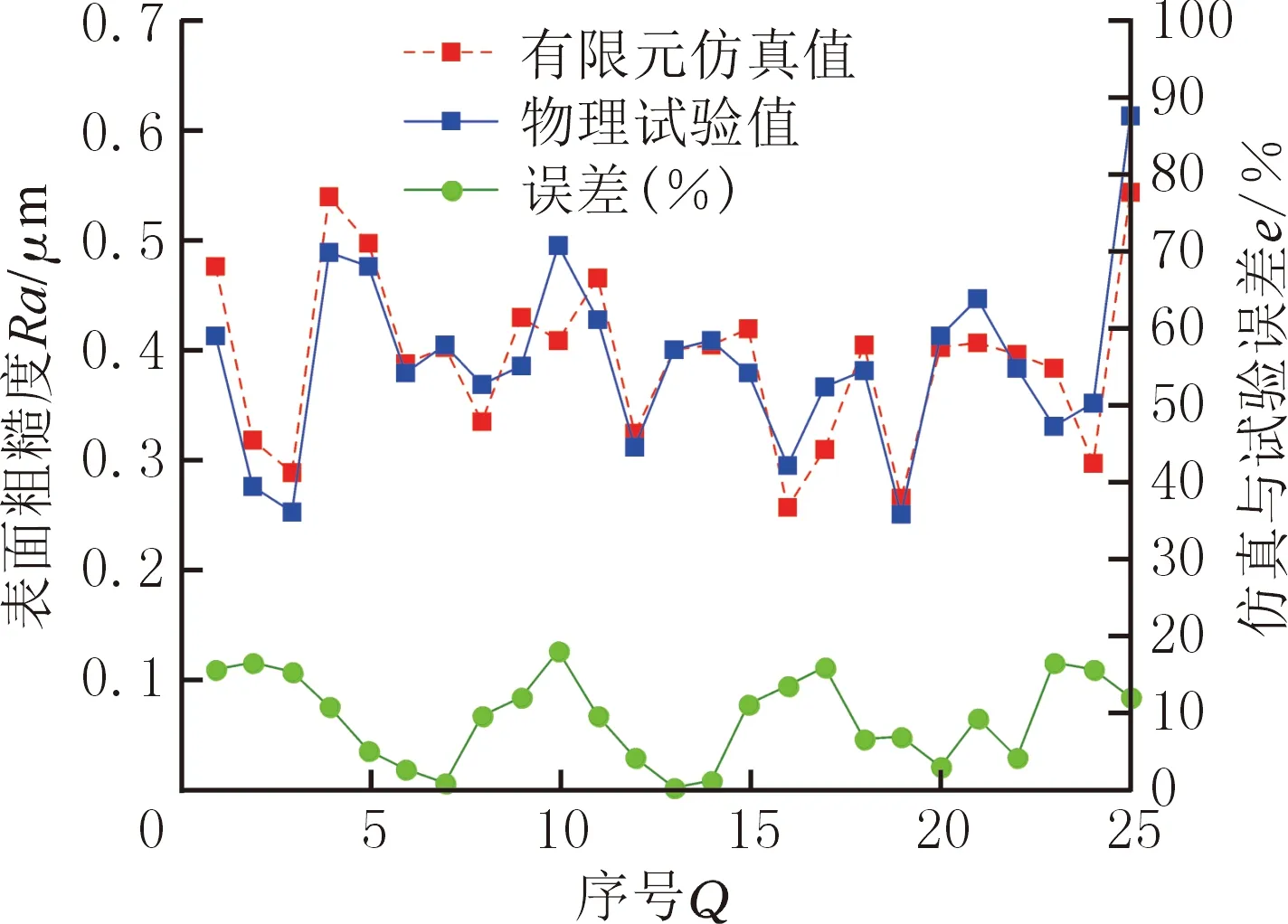
图4 表面粗糙度物理试验数据与仿真数据的对比Fig.4 Contrast of surface roughness data between physical test and simulation

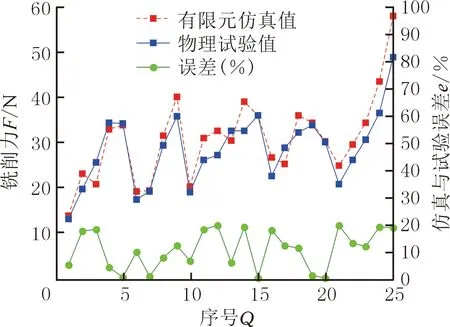
图5 铣削力物理试验数据与仿真数据的对比Fig.5 Contrast of milling force data between physical test and simulation

3 基于能耗与表面粗糙度的多目标优化算法的构建

高斯过程回归(GPR)方法在解决高维度输入、小样本空间和非线性问题上具有较好的性能，适合作为处理第2节正交试验数据的方法。本文采用人工蜂群(ABC)算法改进的GPR模型作为有限元仿真的代理模型，该模型选择适用于非线性关系的平方指数协方差和线性协方差相结合的组合协方差函数[12]，并基于Pareto支配关系，利用多目标粒子群优化(MOPSO)算法，以能耗与表面粗糙度为目标进行加工参数优化，其具体流程如图6所示。

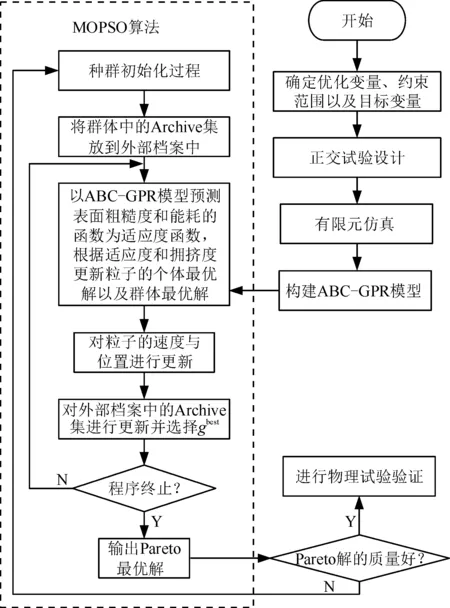
图6 基于ABC-GPR-MOPSO的算法流程Fig.6 Algorithm flow based on ABC-GPR-MOPSO

需要优化的铣削能耗和表面粗糙度之间存在着相互制约的关系。本文采用基于Pareto支配关系的ABC-GPR-MOPSO算法来解决两者之间的优化平衡问题。以铣削四要素为决策变量，以表面粗糙度和能耗为优化目标，其优化问题可以用如下数学公式表达：

(3)

nmin≤n≤nmaxvcmin≤vc≤vcmax

apmin≤ap≤apmaxaemin≤ae≤aemax

ABC-GPR-MOPSO算法优化流程的具体步骤如下：

(1)初始化多目标粒子群的基本参数，见表4。在各决策变量和最大最小粒子速度范围内初始化各粒子的位置xj及对应速度vj，其中j∈[1，K]表示种群数；将本课题组提出的ABC-GPR模型[12]预测表面粗糙度和能耗的函数作为适应度函数，根据Pareto支配原则计算得到存放非劣解的Archive集。

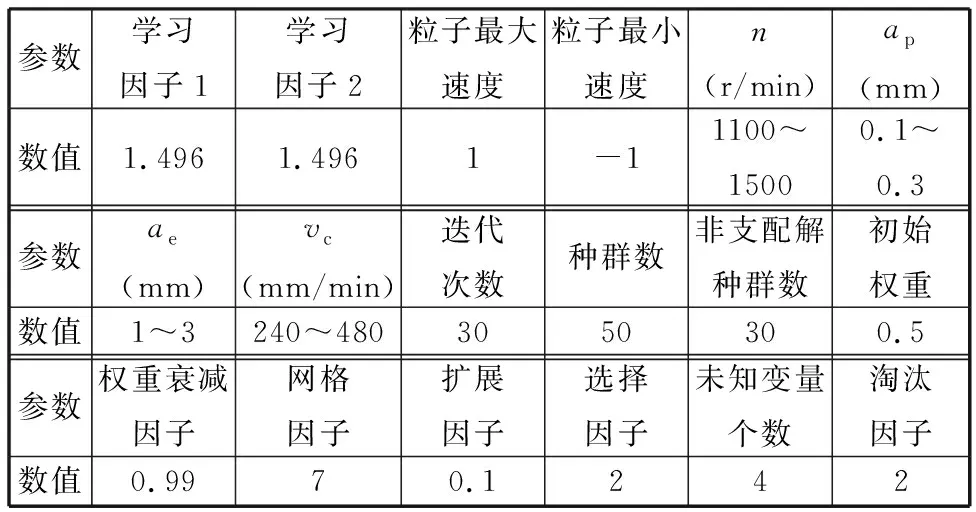
表4 多目标粒子群优化的基本参数设置

(2)根据粒子的适应度值确定个体最优解，当个体最优不能确定时随机选取一个解作为个体历史最优，记为pbest；根据适应度范围和网格扩展因子确定网格范围并对网格进行划分，计算Archive集在网格中的拥挤度，并选择当前全体中拥挤度小的位置(种群最优解)记为gbest。

(3)更新Archive集中粒子的速度、位置，以求解出粒子当前迭代过程中最好的pbest，表达式分别如下：

(4)

(5)

式中，k为当前迭代次数；C0为权重衰减因子；w为惯性权重，w(k+1)=C0w(k)；c1、c2分别为个体与种群学习因子；r1、r2为0～1的随机数。

(4)通过比较当前迭代过程中全部粒子的适应度，将非支配解存储入Archive集中，由此对Archive集进行维护与更新，并选择最优的gbest；当非支配解个数超过设定的个数时，根据设置的淘汰因子和网格自适应重划分规则使其减少到阈值个数。

(5)当迭代次数达到设定的次数时程序就会停止，此时存储在外部档案中的所有解集就是Pareto前沿；若没有达到条件要求则会返回至步骤(1)。

4 结果分析与对比

4.1 ABC-GPR模型的预测效果

将仿真得到的25组数据作为上述ABC-GPR模型的数据集，选取20组仿真数据作为该模型的输入，其中15组作为训练样本，5组作为寻优验证样本，剩余的5组样本作为与预测值对比的测试样本。ABC-GPR模型的表面粗糙度和铣削力预测结果如表5和图7所示，可以看出，两者的仿真值与预测值有较好的吻合度，且铣削力与表面粗糙度的平均绝对百分比误差(MAPE)均较小，均不超过10%，从而验证了该模型的有效性。其中，MAPE的计算表达式如下：

(6)

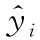
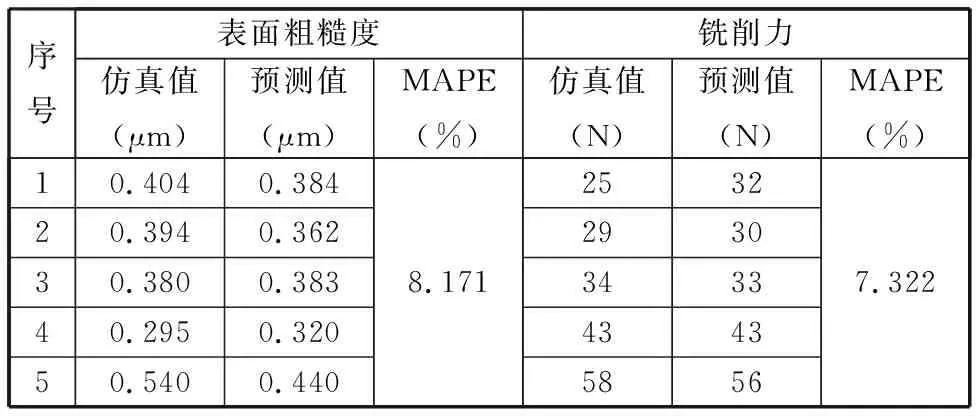
表5 预测值与仿真值的比较

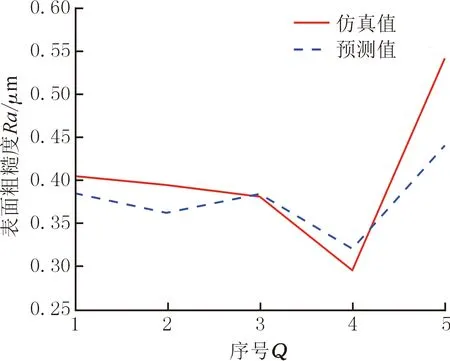
(a) 表面粗糙度

为对比ABC-GPR模型的性能，本文采用灰狼优化 (grey wolf optimization，GWO)算法[13]、粒子群优化(PSO)算法[14]分别优化GPR模型，进而构建GWO-GPR模型和PSO-GPR模型，在上述3种模型下将预测表面粗糙度和能耗的效果进行了对比，分别用模型精度评判指标(均方误差(MSE)、MAPE、决定系数(R2)、对称平均绝对百分比误差(SMAPE))和模型复杂度评判指标(算法运行时间T)来比较。其中，MSE、R2和SMAPE的计算表达式分别如下：

(7)

(8)

(9)

其中，VSSE为残余均方根误差；VSST为方差总和。

各优化算法依据式(6)～式(9)计算得到的各指标结果如表6所示。为了方便对比，将表面粗糙度和铣削力预测效果较优的结果用下划线标出。综合来看，ABC-GPR模型的效果最优。其中表面粗糙度的R2值相对较小，只是表5中第5组表面粗糙度的预测值与仿真值偏差相对略大。表面粗糙度值Ra的定义是基于工件加工表面的轮廓线计算得到的，而在加工过程中的刀具跳动、机床颤振等都会对工件加工表面形成的轮廓线产生影响[15-16]，从而导致表面粗糙度值出现波动，可能造成个别点预测误差偏大，影响了R2指标的结果。在一般的机加工中，通常更关心表面粗糙度是否偏离精度等级的范围，而基于图7的预测趋势和MSE、MAPE和SMAPE这些反映偏差的指标来说，预测趋势符合仿真模拟趋势，预测值与仿真值的平均偏差较小，两个表示百分比的指标(MAPE和SMAPE)都在10%以内，因此，可以认为利用ABC-GPR模型预测表面粗糙度是具有可行性的。

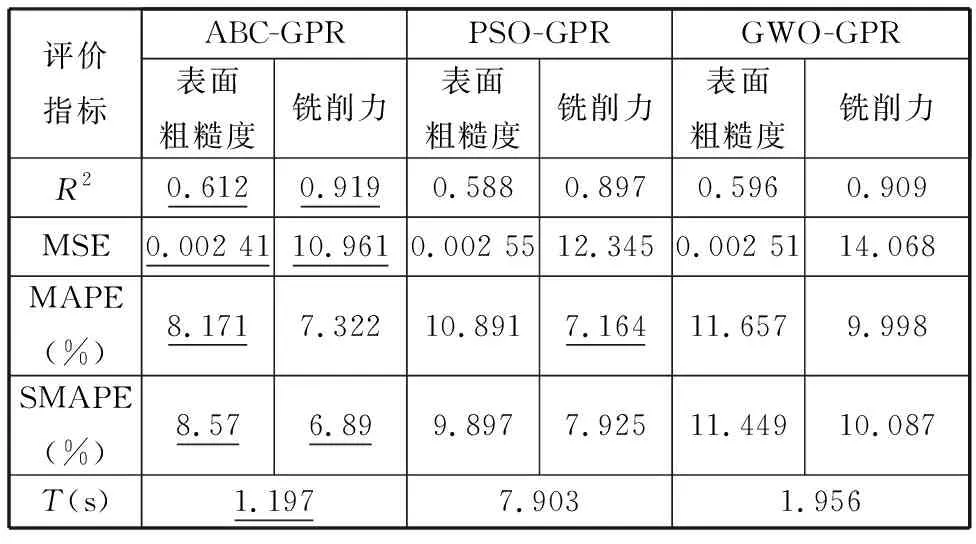
表6 ABC、PSO及GWO在各指标下的结果

4.2 多目标优化结果及其验证

运行ABC-GPR-MOPSO算法程序的结果如图8所示，其中红色点不被其他点支配(Pareto前沿)，黑色点完全被其他点支配，蓝色点为个体最优解对应的目标值。各铣削参数下Pareto前沿以及目标值如表7所示。在此选取其中一组优化后的参数{n，ae，ap，vc}={1449 r/min，1.7 mm，0.21 mm，412 mm/min}，其对应的表面粗糙度和单位体积能耗分别为：0.259 μm，252 J/mm3，将该组参数进行物理试验，以验证ABC-GPR-MOPSO方法的有效性。

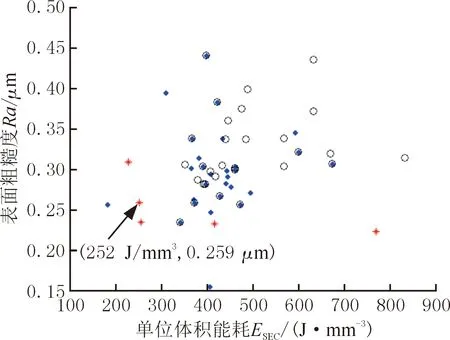
图8 ABC-GPR-MOPSO算法的Pareto解(红色点)Fig.8 Pareto solution of ABC-GPR-MOPSO algorithm(red dot)

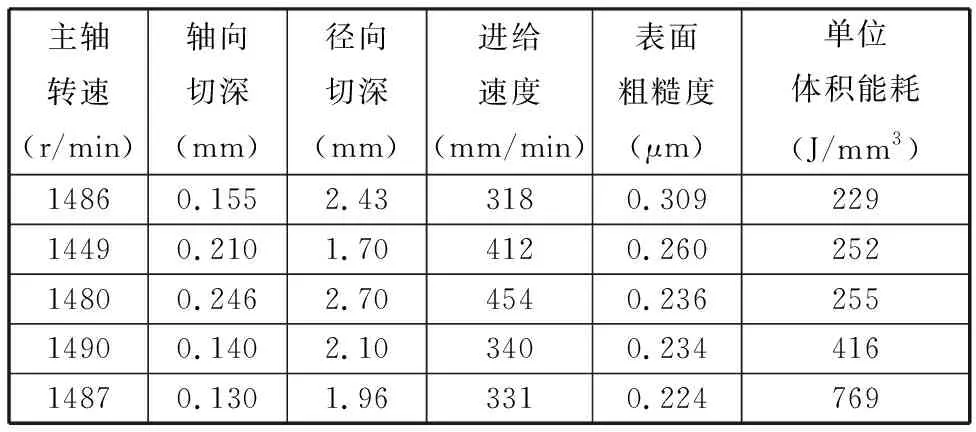
表7 多目标优化的结果

基于第2节搭建的试验平台，输入优化后的铣削参数，通过试验可得到对应的表面粗糙度和单位体积能耗。为了避免偶然性，对这组参数重复进行5次试验，得到的结果如表8所示。由计算可知，单位体积能耗和表面粗糙度与对应优化结果的平均误差分别为9%和9.9%，该组优化后的铣削参数满足实际加工期望达到的效果，可用于指导铣削钛合金生产加工。

表8 表面粗糙度与单位体积能耗的试验值

5 结论

(1)基于Deform-3D软件的有限元铣削加工模型所得到的仿真表面粗糙度值与铣削力值，与它们对应的物理试验测量值具有相同的变化趋势，且表面粗糙度和铣削力的误差均值分别为9.11%和10.50%，因此可采用仿真软件获得的数据代替物理试验数据进行参数优化，从而可有效降低物理试验的成本。

(2) 在人工蜂群(ABC)算法优化的高斯过程回归(GPR)代理模型对表面粗糙度与铣削力的预测中，ABC算法的预测精度优于已有文献中的灰狼优化(GWO)算法和粒子群优化(PSO)算法的预测精度，ABC算法的耗时也最少。

(3)在ABC-GPR代理模型产生的工艺参数与表面粗糙度和单位体积能耗之间的映射关系的基础上，利用多目标粒子群优化(MOPSO)算法得到表面粗糙度与单位体积能耗的Pareto前沿，并利用物理试验验证了该结果的有效性，从而证明了ABC-GPR-MOPSO算法的可行性。