地铁隧道小净距下穿地下洞室振速控制研究
陈 沛,吴剑锋,蒙云琪,张兆龙,李小贝,何 理
(1.中铁四院集团工程建设有限责任公司,武汉 430063;2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,武汉 430065)
在《交通强国建设纲要》的引领下,我国城市轨道交通迅猛发展,地下交通隧道的建设处于繁忙时期。城市地铁隧道穿越地下复杂岩层的工程项目屡见不鲜[1-2],坚硬岩层及破碎软弱岩层对地铁隧道掘进带来不利影响,但制约地铁隧道施工进度的关键因素往往为隧道爆破掘进引发周围环境构筑物的不利振动[3-4],譬如地下人防洞室结构、地下浅表城市管线、地表林立的城市建筑等。为有效减弱地铁隧道爆破对邻近建筑物的影响,大多可采用数码电子雷管精确延时控制隧道掌子面的单段药量[5],如此能够有效控制爆破振动效应。数值模拟方法已广泛应用在交通隧道爆破掘进的振动影响研究中[6-7],研究表明,有限元数值模拟能够较为贴近的表明隧道掘进爆破对周围建筑物的影响趋势与重点危险区域。对于地铁隧道爆破对邻近结构的影响研究,吴昊[8]以工程实际经验为例,介绍了2 m内净距的地铁隧道的爆破掘进方案,并以加固支护为主,辅以数值模拟手段取得了较好工程效果。薛宪彬[9]研究了地铁隧道爆破振动影响下多层砌体结构振动信号的变化规律,汪平等[10]研究了浅埋隧道爆破振动传播的规律和监测技术。陈桂龙等[11]以工程实际与数值模拟结合,研讨了不同影响因素下,地铁隧道爆破振动对地表建筑群的影响规律,诸如此类的研究较多。然而地铁隧道小净距下穿地下人防结构的爆破振动响应研究不够全面。
针对上述问题,基于武汉市地铁5号线彭刘杨站~司门口站区间隧道下穿武汉市人防工程爆破施工项目,最近距离仅4.2 m,首先利用ANSYS-Lsdyna动力有限元软件建立高精度毫秒延时掏槽起爆模型,探究距离人防工程小净距下地铁隧道掏槽孔起爆的最佳延时时间。通过在邻近人防洞室布设爆破振动监测点进行跟踪监测,并精确控制起爆网路的起爆时序和最大单段药量进行施工现场试验。而将数值模拟与实测数据结果进行对比分析,验证有限元方法的有效性。最后总结得出坚硬岩石邻近地下人防洞室小净距爆破开挖的最佳爆破参数与数码雷管网路延时时间设置参数。
1 工程项目概况
1.1 工程背景
武汉地铁5号线彭刘杨站~司门口站区间左右线隧道分别开挖,区间左、右线间距为15~19 m(净距7.8~11.8 m),双线隧道设计轨面高程右线10.96~10.31 m,左线10.99~10.31 m,隧道开挖直径7.1 m。
开挖隧道区间在蛇山景区处下穿既有防空洞和繁忙的京广铁路。区间隧道顶部与此处防空洞间距约为4.2 m,距离京广铁路26.3 m,与黄鹤楼主楼底层地坪垂直高差约42.1 m,水平距离约74.65 m;与圣像宝塔地坪垂直高差约35.25 m,水平距离约33.22 m。爆破施工时,控制爆破振动,减少对既有人防工程和黄鹤楼景区运营的影响为爆破振动控制的重点。地铁暗挖隧道与周围建筑结构相对位置及与人防结构高程相对位置如图1、图2所示。

注:1-圣像宝塔;2-人防洞室;3-黄鹤楼;4-左线隧道;5-右线隧道。图1 地铁隧道与周围建筑结构相对位置Fig.1 Relative position between the metro and surrounding building structures

图2 地铁隧道与人防结构高程相对位置Fig.2 Relative position of elevation between the metro tunnel and civil air defense structures
1.2 爆破设计及振动监测方案
地铁5号线彭刘杨站~司门口站区间下穿蛇山人防及京广铁路段全部位于强风化石英砂岩及中风化石英砂岩层中,隧道围岩分级为II、III级,围岩强度较高。下穿人防工程区段隧道采用上下台阶法爆破开挖,尽量拉开同时爆破的工作面距离,减小爆破振动的叠加,上下台阶距离5~10 m间隔开挖。左、右线隧道典型爆破断面为直径7.1 m。上台阶采用楔形掏槽方式,严格按设计开挖轮廓线布置周边孔及辅助孔,爆破采用2#岩石乳化炸药,起爆网路采用电子数码雷管组网;下台阶采用水平结合垂直钻孔方式来控制爆破振动,以减小爆破振动叠加的可能。上下台阶炮孔布置如图3所示。

注:序号1~13为起爆顺序。图3 上下台阶炮孔Fig.3 Blast hole of upper and lower bench
在按照设计爆破方案实施爆破作业时,对邻近人防工程洞室设置移动爆破振动监测点,爆破振动监测点跟随每次隧道掌子面移动而移动,同一位置设置2台仪器,避免偶然故障发生。监测点放置位置选取在人防洞室靠近地铁隧道一侧坚硬地面处,隧道掘进过程人防洞室监测点布置如图4所示。根据《爆破安全规程》(GB 6722-2014)中规定交通隧道,采用保护对象所在地质点峰值振动速度,其振动最大允许值为10~20 cm/s。项目实施过程中因人防工程与新建隧道净距仅为4.2 m,且人防工程结构坚固,抗冲击能力较强,截面小,故选取安全振动控制值为20 cm/s,经过爆破参数优化及选用适宜的数码电子雷管网路延时时间,隧道爆破振动对人防洞室振动影响大大降低。

图4 人防洞室监测点布置Fig.4 Layout of monitoring points in civil air defense cavern
爆破施工过程中,研究振动监测数据时发现,引起人防洞室结构振动的主要振源是由掏槽孔爆破所致,因此研究如何减弱掏槽孔炸药爆炸引起的振动是降低地铁5号线隧道爆破振动危害的关键。
2 质点峰值振动速度衰减规律
对于爆破应力波对中、远区的振动破坏效应,利用萨道夫斯基公式计算所得出的振动速度分布与实测振动数据分布存在一定误差[12],因此许多学者对爆破引起的质点峰值振动速度衰减公式做了进一步改进[13]。
对于柱状装药,在C-J爆轰条件下,炸药爆炸的平均爆轰压力表示为
(1)
式中:pe为炸药平均爆轰压力;ρe为炸药密度;D为炸药爆轰速度;γ为炸药的等熵指数。
假设爆生气体为多方气体,则其状态方程为
(2)
式中:p为某一状态下的爆生气体压力;ρa为某一状态下爆生气体的密度;A为常数;ν0为爆生气体的等熵指数。
当p≥pk时,取ν0=γ=3.0;当p 对于耦合装药条件,有p0=pe;对于不耦合装药条件,如果装药时的不耦合系数b/a值较小(a为装药直径),则爆生气体的膨胀只经过p>pk一个状态,则此时由式(2)得到炮孔初始平均压力p0为 (3) 如果装药的不耦合系数值较大,此时爆生气体的膨胀需经历p≥pk及p (4) 把式(3)或者式(4)代入炮孔壁上质点峰值振动速度公式:u0=p0/ρcp中去,则可得到不耦合装药条件下炮孔壁上的质点峰值振动速度u0。 在多孔同时起爆的条件下,质点峰值振动速度公式可反应诸如炸药种类、炸药特性、钻孔孔径、装药结构及岩石性能参数等因素对质点峰值振动速度的影响,其修正公式为 (5) 式中:k′为多孔同时起爆条件下的修正系数,主要与同时起爆的炮孔个数、振速测算点与同时起爆炮孔连线的相对位置等参数有关。 基于动力有限元ANSYS-Lsdyna平台进行数值模拟分析,对于人防洞室和隧道周围岩石均采用HJC材料模型,该材料模型能够比较好的模拟岩石及混凝土材料在高应变率下的大变形相关问题,对于岩石在高速碰撞下的力学行为相关问题上表现较好[14]。该材料模型通常适用于Lagrange算法及Euler算法中。HJC仅有材料模型,无状态方程,主要包括状态方程、屈服面方程以及演化方程3个方程[15]。HJC材料模型的方程形式以及各项材料参数含义在此不多赘叙(见表1)。 表1 材料参数Table 1 Material parameters 模型中爆破荷载的加载方式以炮孔壁面施加冲击荷载的方式实现,将炮孔内部炸药爆炸的压力时程曲线简化为三角形荷载。为研究掏槽孔延时爆破的振动效应,根据设计方案,选取掏槽孔施加爆破冲击荷载的顺序如图5所示,图中数字1~5代表掏槽孔荷载施加顺序。 图5 掏槽孔施加荷载顺序Fig.5 Loading sequence of cut hole 炸药在岩体中爆破是一个非常复杂的力学过程,由于炸药在炮孔内部爆炸的机制难以被现在的有限元数值方法模拟,尤其是炮孔内部炸药爆轰、爆轰波及爆生气体将岩石粉碎进而发展到激发弹性地震波这一复杂的过程,因此需要一种等效模拟办法。地铁隧道毫秒延时掏槽有限元模型是采用等效弹性边界的模拟方法[16-17],炮孔周围的岩体根据破坏程度可分为 3类:粉碎区、破碎区、弹性振动区,将整个非弹性区作为爆源,在掏槽孔群孔起爆时的等效边界即为各孔各自所形成的破碎区的包络线。则在模拟时,将随时间变化的压强荷载施加在掏槽孔非弹性区形成的包络线的面上(见图6)。 图6 隧道毫秒延时掏槽有限元模型Fig.6 Finite element model of millisecond delay cutting in metro tunnel 根据人防洞室与新建地铁隧道的相对位置关系建立精细化数值模型,掏槽孔等效边界范围近似取r=10r0(r0为实际炮孔半径),计算区域为30 m×28 m×3.6 m,为防止模型边界反射应力波,岩体外包面均采用非反射边界条件设置。等效边界爆破荷载施加在掏槽孔等效弹性边界面上,冲击荷载压力峰值为56 MPa,载荷上升时间为0.7 ms,持续时间为8.0 ms。根据图5中掏槽孔延时起爆的顺序,设置各个掏槽孔群的等效弹性边界,利用*DEFINE_ELEMENT_DEATH_SOLID_SET关键字实现等效弹性边界内单元。计算模型单元总数为203 970个,具体三维有限元模型如图6所示。 为初步验证所建立的有限元数值模型对人防洞室结构振动规律的有效性,将现场振动监测数据和与之对应工况的数值模拟结果进行对比,所参照的掏槽孔的延时时间设置为:图5中所示掏槽序号,1所示主掏槽与2所示一级掏槽间隔时间t1=150 ms,2所示一级掏槽孔与3所示一级掏槽间隔时间t2=10 ms,3所示一级掏槽与4所示二级掏槽间隔时间t1=150 ms,4所示二级掏槽与5所示二级掏槽间隔时间t2=10 ms。选取人防洞室靠近新建隧道一侧洞室底角的振动监测数据与数值模拟x方向上振动速度时程曲线(见图7)可知,两者数据曲线分布规律接近,峰值大小接近,表明所建立的有限元数值模型能够较真实地反映地铁5号线隧道掘进掏槽爆破对人防结构影响的振动特性。 图7 人防洞室振动时程Fig.7 Vibration time history of civil air defense cavern 为了探寻对人防洞室振动影响最小情况下的最佳掏槽延时时间,设置了11种模拟工况(见表2),得到数值模拟结果产生的峰值振速分布情况如图8所示。由结果分析可知,随着不同掏槽起爆延时时间以及同一级掏槽起爆延时时间的增加,掏槽孔对人防洞室所造成的振动是呈减小趋势,且随着延时时间的增加,人防结构振动速度逐渐趋于平稳,变化不大。考虑到爆炸冲击波在近处传播,延时时间较长时,爆炸冲击波基本不叠加,相当于单个冲击波对人防洞室作用,再增加延时时间意义不大。由图8中可知,在地铁5号线工程背景下的不同级别掏槽起爆适宜延时时间为10 ms,同一级别掏槽起爆适宜延时时间为6 ms。 表2 不同延时时间下的人防结构振动值Table 2 Vibration value of civil air defense structure under different delay time 图8 数值模拟峰值振速分布情况Fig.8 Distribution of peak velocity by numerical simulation 在地铁5号线的爆破掘进项目中,根据数值模拟结果得出的各级掏槽最佳延时时间的结果开展爆破施工,实际装药参数根据现场断面情况不同而进行调整,得到地铁5号线隧道爆破对邻近人防洞室振动监测数据如表3所示。根据表3所示结果可知,在地铁5号线工程地质条件下,数码电子雷管组网参数采取上文所述最佳延时时间的前提下,合理的最大单段起爆药量为0.6 kg。在采取该单段药量,人防结构振动速度最低为12.76 cm/s,在施工过程中保障了相邻人防洞室的安全。 表3 人防振速监测Table 3 Monitoring of civil air defense vibration velocity 1)采用等效弹性边界载荷加载的有限元数值模拟方法,模拟复杂环境下地铁隧道掏槽爆破振动是合理的,能够较好地模拟爆破振动对小净距下的人防洞室的振动规律。 2)通过数值模拟方法和工程实践结果可以得出,在武汉地铁5号线工程背景下,对掏槽孔而言,隧道不同级别掏槽起爆适宜延时时间为10 ms,同一级别掏槽起爆适宜延时时间为6 ms。 3)经5号线工程实践总结,在隧道围岩分级为II、III级情况下,采用数码电子雷管起爆网路,在地铁隧道与邻近人防洞室仅相距4.2 m的小净距隧道爆破适宜最大单段掏槽药量为0.6 kg,可为类似小净距隧道爆破提供借鉴和参考。3 数值模型的建立
3.1 材料模型及载荷输入

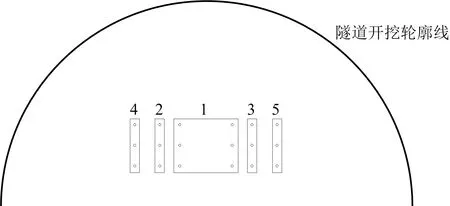
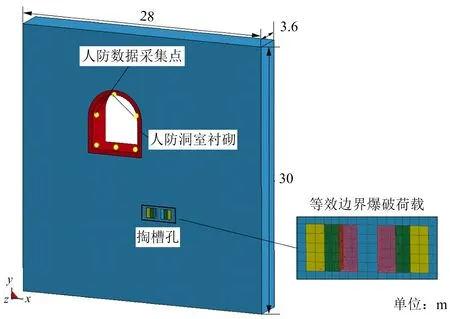
3.2 隧道毫秒延时掏槽有限元模型
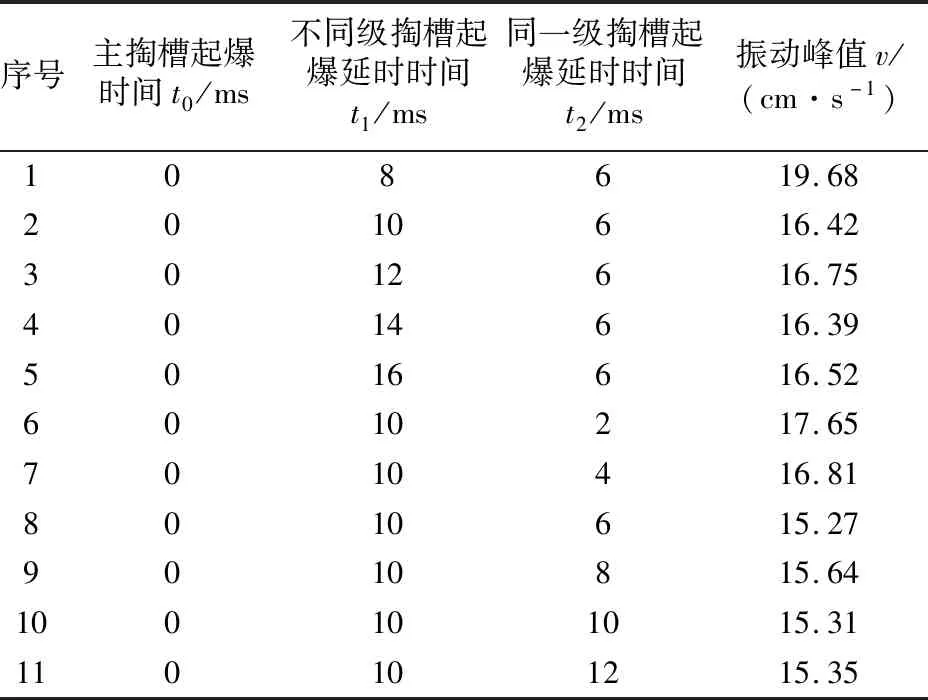
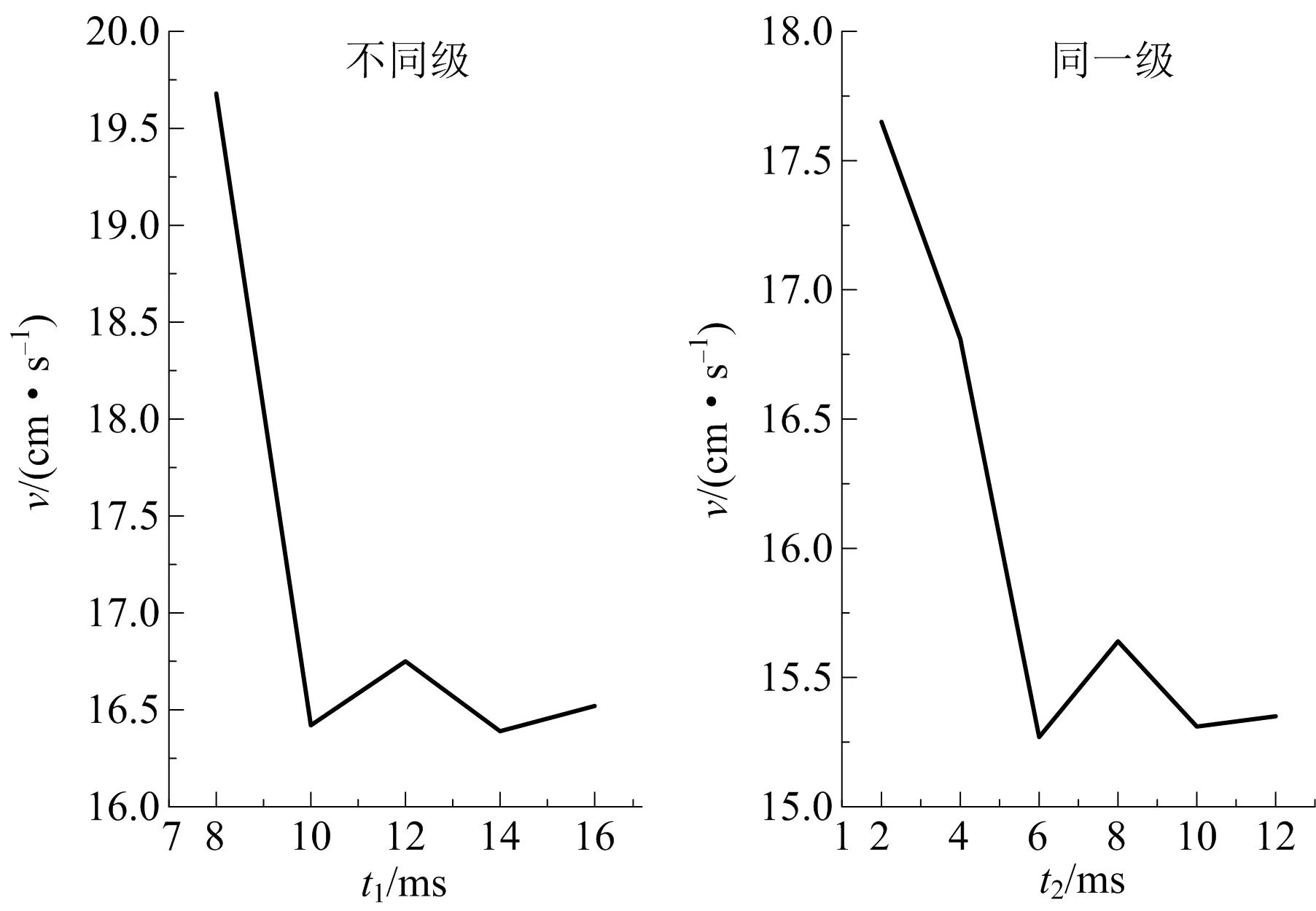
4 结果对比分析


5 结论

