包覆泡沫铝钢梁动态位移的计算及影响因素

康建功，孙妙娟

(重庆财经学院，重庆 401320)

泡沫铝是在纯铝或铝合金中加入添加剂后，经过发泡工艺而成的新型材料，它具有质轻、比吸能高、比强度高、减振降噪、缓冲吸能等特性，受到军工、航天、交通等领域学者关注，将其作为爆炸冲击波吸收材料是学者们研究的重点方向之一。A.G.Hanssen等[1]利用自制钟摆研究表明，在近距离爆炸荷载作用下，增加泡沫铝夹芯板增大钟摆爆炸荷载的冲量，与衰减爆炸荷载结论相反。I.Elnasri等[2]研究表明增加Cymat泡沫需要增加更大的穿透力才可以钻透冲击对象。Liu Z等[3]研究表明增加泡沫铝可以减小圆管在爆炸荷载作用下的变形，提高钢管抗内爆炸的性能。Guruprasad等[4]研究表明包覆泡沫铝缓冲层能够有效减小爆炸荷载的作用。Jin Zeyu等[5]的研究表明在爆炸荷载作用下，包覆泡沫铝缓冲层具有最优厚度，如果包覆的厚度不当，可能出现增大结构上的爆炸荷载。综上，不同研究思路，不同试验方法，不同研究对象得到的结论不尽相同，因此，包覆泡沫铝能否减小结构在爆炸荷载作用下的动力响应及其影响因素值得深入研究。

研究包覆泡沫铝后结构的动力响应，首先需要确定作用在结构上的爆炸荷载。对于包覆泡沫铝后结构上作用爆炸荷载大小同样是研究者面临的重要且迫切需要解决的问题之一。计算结构上爆炸荷载的方法通常为Taylor的经典反射波理论[6]。在刚性反射理论的基础上，Taylor又提出考虑可压缩体结构上爆炸荷载的反射压力值计算方法。随后N.Kambouchev等[7]在Taylor研究的基础上又进行了扩展，加入了可以考虑部分塑性压缩因素影响的流固耦合(FSI)效应。除了迎爆面材料对爆炸荷载大小影响外，Martien Teich等[8]研究表明，结构刚度越小，则爆炸荷载的反射压力和经典理论计算差别越显著，流体-结构作用效应越明显。同样由N.Kambouchev等[9]研究可知，FSI效应还与爆炸荷载作用对象质量的大小有一定的关系。

综上，包覆泡沫铝缓冲吸能层对减小结构抵抗爆炸荷载作用是否有效，如果有效，与哪些因素有关，这些因素如何影响其衰减爆炸荷载的作用等问题均没有达成共识，还需要进行比较深入、细致的研究。为此，开展构件层面的相关研究。首先分析包覆泡沫铝后考虑FSI作用时，钢梁在爆炸荷载作用下荷载的变化情况。并运用有限元法计算包覆泡沫铝钢梁在爆炸荷载作用下动力响应。主要分析材料厚度、屈服强度等因素对泡沫铝衰减钢梁爆炸荷载作用及其动力响应影响情况的一般规律。以期为包覆泡沫铝结构在爆炸荷载作用下的动力响应提供理论参考。

1 计算模型及验证

1.1 研究对象

Martien Teich等[8]研究显示，结构刚度越小，则爆炸荷载作用在其上的反射压力和经典理论计算差别越显著，FSI效应越明显。钢结构相比于混凝土结构是一种轻质柔性的结构，故选用钢梁作为研究对象。同时为保证研究结果的可靠性，基于文献[10]试验条件下展开研究。研究对象如图1所示，一工字形钢梁，两端简支，梁长为L，截面尺寸为160 mm×102 mm×6.6 mm×10.3 mm (梁高×翼缘宽×腹板厚×翼缘高)。考察在爆炸荷载作用下梁的动力响应，包覆泡沫铝缓冲层后，钢梁与未包覆之前的动态响应差异。影响包覆泡沫铝钢梁动态响应的因素等，文章仅考虑梁上方的爆炸荷载作用，不考虑侧向荷载的影响。泡沫铝与梁之间采用直接耦合，不考虑两者的滑移。

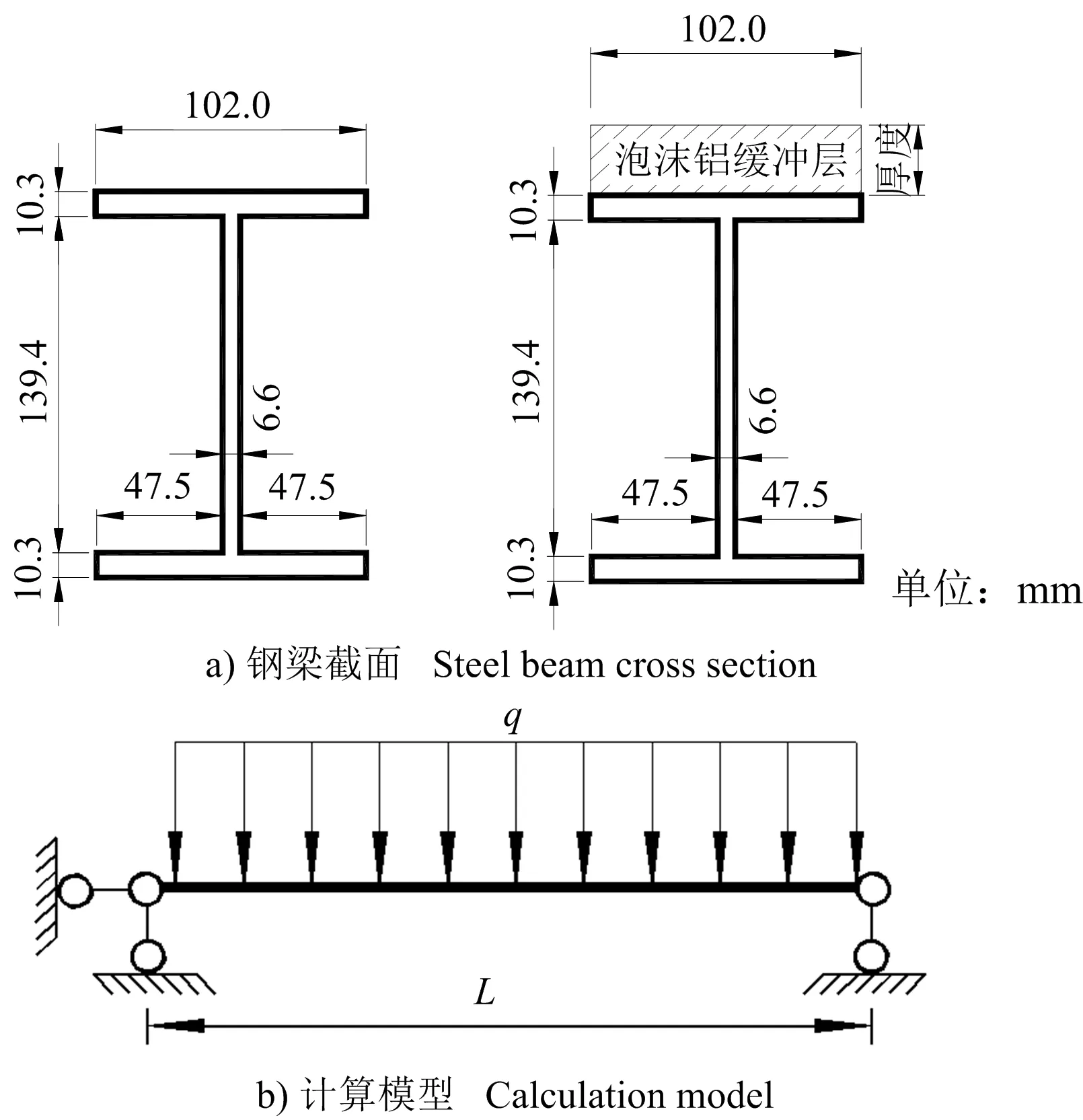
图1 钢梁截面及计算模型Fig.1 Steel beam cross section and calculation model

1.2 FSI理论基础

炸药在空气中爆炸时，远场空气中的爆炸冲击波压力时程曲线通常以指数衰减形式表示[9]：

(1)

式中：p(t)为空气中压力时程曲线；ps为计算点处测量得到的空气冲击波超压值；ti为空气冲击波正相超压持续时间。

在计算相应位置上结构所承受的爆炸荷载时，经典理论假定结构是刚性且固定不动的。空气冲击波作用在结构上爆炸荷载峰值压力通常用下式计算[11]：

(2)

式中:pr为结构上作用的冲击波峰值压力；p0空气初始压力值；CR为反射系数，通常情况下2≤CR≤8。

计算结构在爆炸荷载作用下的动力响应时，通过将作用在结构上的爆炸荷载简化成峰值压力为pr、持续时间为ti无升压时间的三角形荷载。

以上简化基于结构为刚性且固定不动假设，而包覆泡沫铝后的结构能否满足此条件值得商榷。由于泡沫铝在爆炸荷载作用下会产生塑性变形，从而消耗掉一部分爆炸冲击波能量，这种变化是否会引起原假设条件的变化值得讨论。N.Kambouchev[7]及Martien Teich等[8]通过理论研究发现，结构包覆泡沫铝等此类塑性变形缓冲层时，由于流体-结构作用效应导致作用在结构上的冲量出现与以上简化计算不尽相同的情况。同时给出结构上反射冲量(作用在结构上的冲量)与空气入射冲量(空气中相应位置的冲量)比值的计算公式：

(3)

式中：Ip为结构反射冲量，即作用在结构上的冲量；Ii为入射冲量，即结构所在位置上空气中的冲量；β0为塑性变形材料压实前后体积比。

同时，Nayden Kambouchev等[9]通过数值计算给出结构上作用冲击波冲量与入射波冲量比值公式：

(4)

根据以上FSI理论绘制出横轴为包覆材料压缩前后体积比β0与纵轴为结构上反射系数CR的关系(见图2),可以看出，随着包覆材料压缩性的提高，作用在结构上的冲量呈指数递减。极限情况下，当介质可无限压缩时，爆炸荷载作用在其上的冲量可减少至零。而考虑材料塑性吸能条件下较不考虑时的反射系数小，符合能量守恒的普适规律。

最后，利用闵可夫斯基和对图16a与图16b进行累积，结合式(28)得到faFM和waFM的累积T-Map在Lv和Q方向的2维空间域(图17)。图17即为机身—机翼交点轴线中所有满足Mv=0和P=0的交点装配偏差波动范围。

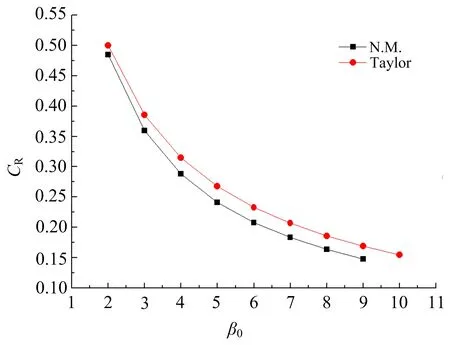
图2 CR与β0关系Fig.2 Relation between CR and β0

为验证以上理论在工程应用中的注意事项，开展以下研究工作。首先计算考虑FSI效应下包覆泡沫铝钢梁的动力响应；然后计算不考虑FSI效应下包覆泡沫铝钢梁的动力响应；最后研究其他因素(如泡沫铝厚度、泡沫铝屈服强度等)对包覆泡沫铝钢梁动力响应的影响情况。

1.3 材料参数

钢材模型采用理想弹塑性模型，密度ρ=7 800 kg/m3、弹性模量E=2 100 GPa、屈服强度σy=400 MPa。材料率效应采用Cowper-Symonds模型，其中应变率常数分别取C=40.4、q=5[11]。泡沫铝采用石少卿等[12]所研究的闭孔泡沫铝，其静态应力应变曲线如图3所示。图中分别给出了泡沫铝平均密度为0.48 g/cm3，相对密度(泡沫铝密度/铝密度)为0.18,以及平均密度为0.45 g/cm3相对密度为0.17的泡沫铝应力应变曲线。计算的泡沫铝模型同Elnasri等[2]采用Honey-comb模型，该模型需要输入应力应变曲线。

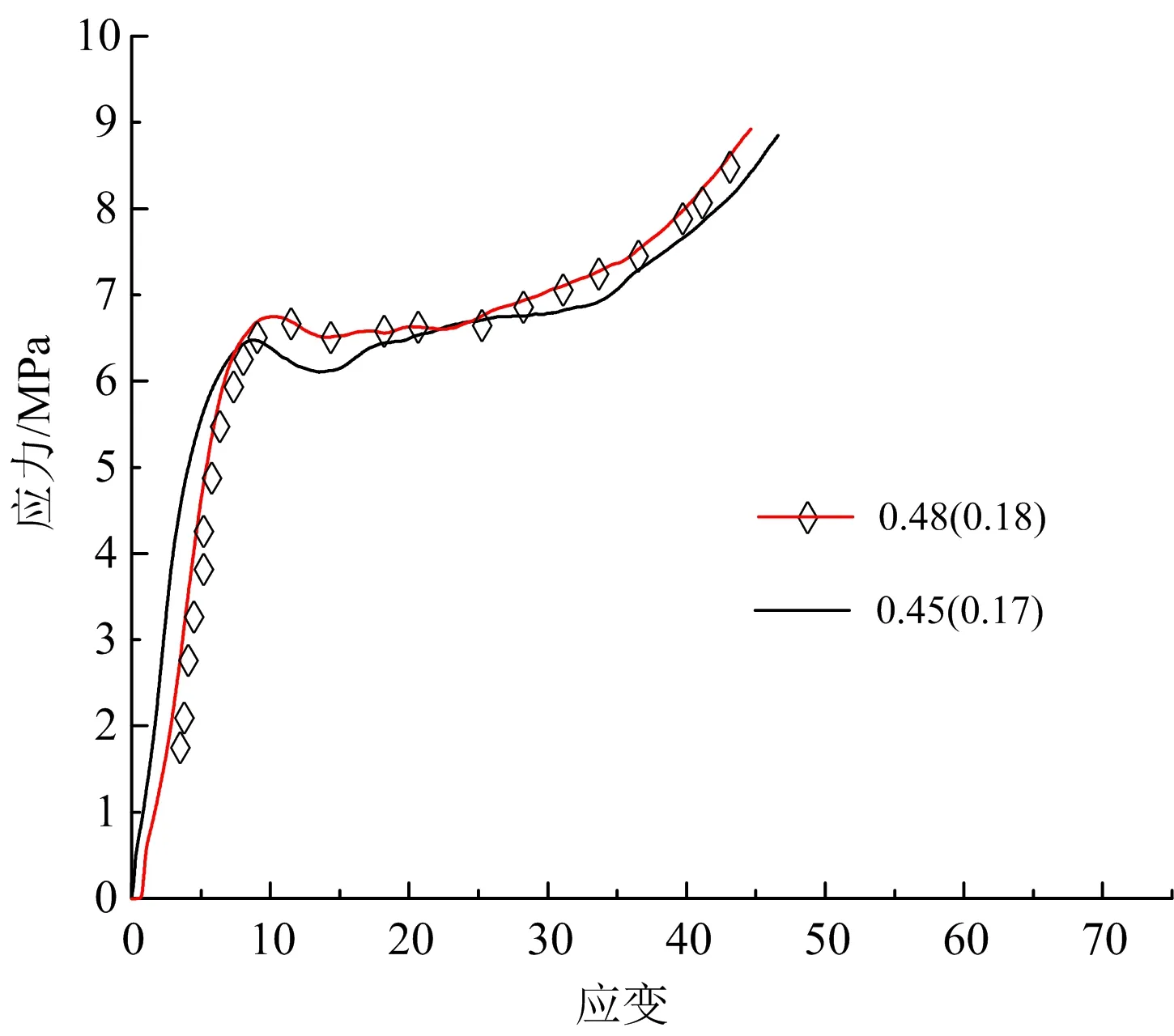
图3 泡沫铝应力应变Fig.3 Stress strain of aluminum foam

为简化计算，且考虑泡沫铝吸能主要是塑性阶段，将泡沫铝应力应变曲线简化成两折线模型(见图4)。压实前，将其简化成屈服强度的理想塑性材料，压实后简化成实体材料的屈服段与压实前的连线，这样可以减少计算时间又能体现泡沫铝平台吸能的主要特性[13-15]。

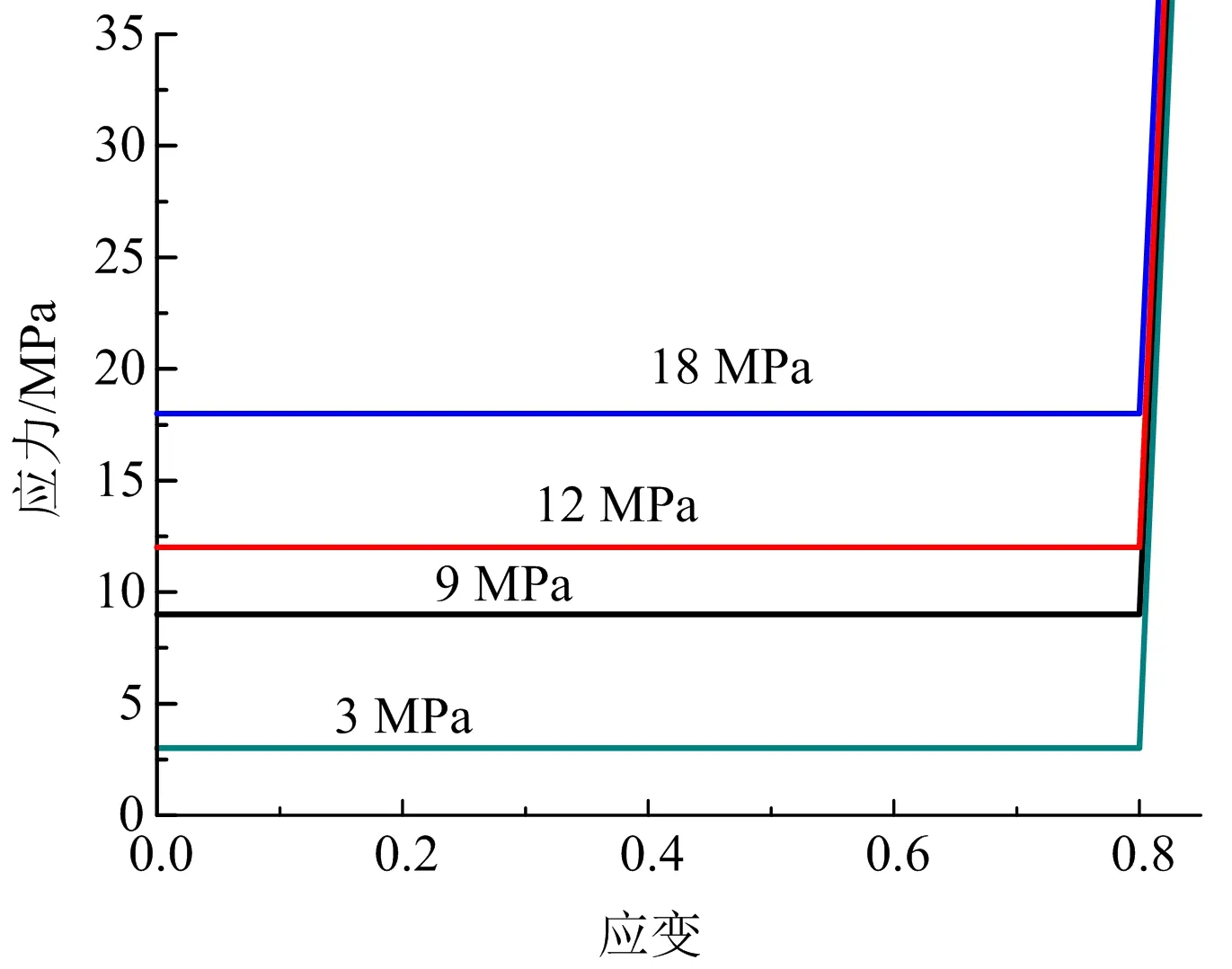
注：3、9、12、18 MPa均为理想塑性材料的屈服强度数值。图4 简化泡沫铝应力应变Fig.4 Simplified stress strain of aluminum foam

1.4 模型验证

计算方法可靠是研究结果正确的保证，计算结果与试验结果的对比是验证计算方法的重要途径。首先对文献[10]给定条件下的工字钢梁在爆炸荷载作用下的动态响应进行模拟。钢梁在爆炸荷载作用下等效应力与变形如图5所示。

注：t=3.4 ms。图5 梁等效应力与变形Fig.5 Eqivalent stress and deformation of steel beam

由试验测量值与数值模拟结果对比(见图6)可知，试验梁跨中变形时程曲线值与数值模拟结果时程曲线基本吻合。梁跨中最大变形值误差分别为2%(见图6a)与9%(见图6b)。计算误差在工程允许范围内，可用于相关问题的研究。

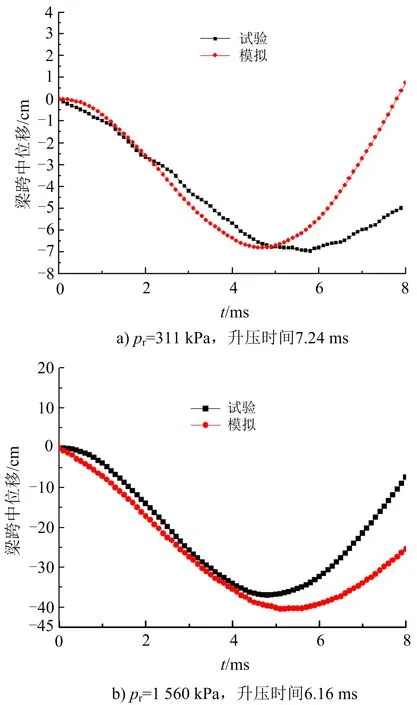
图6 计算结果与试验结果对比Fig.6 Comparison of calculate and experimental results

2 计算结果分析

基于流固耦合效应，对是否考虑该效应时钢梁在爆炸荷载作用下的动力响应变化进行研究，并将计算结果与有限元法计算包覆泡沫铝钢梁在爆炸荷载作用下的动力响应结果进行对比。

2.1 FSI效应的影响

由不考虑FSI效应、考虑FSI效应及N.M效应条件下，钢梁跨中位移时程曲线(见图7)对比结果可以看出，考虑FSI效应的梁跨中最大变形较不考虑FSI效应时小；考虑FSI效应的结果为不考虑FSI效应结果的87%，考虑N.M效应的结果为不考虑FSI效应结果的81%。增加40 mm厚泡沫铝包覆层后运用有限元法计算的梁跨中位移时程曲线与不增加泡沫铝梁直接考虑FSI效应计算得出的位移时程曲线对比如图7b所示。

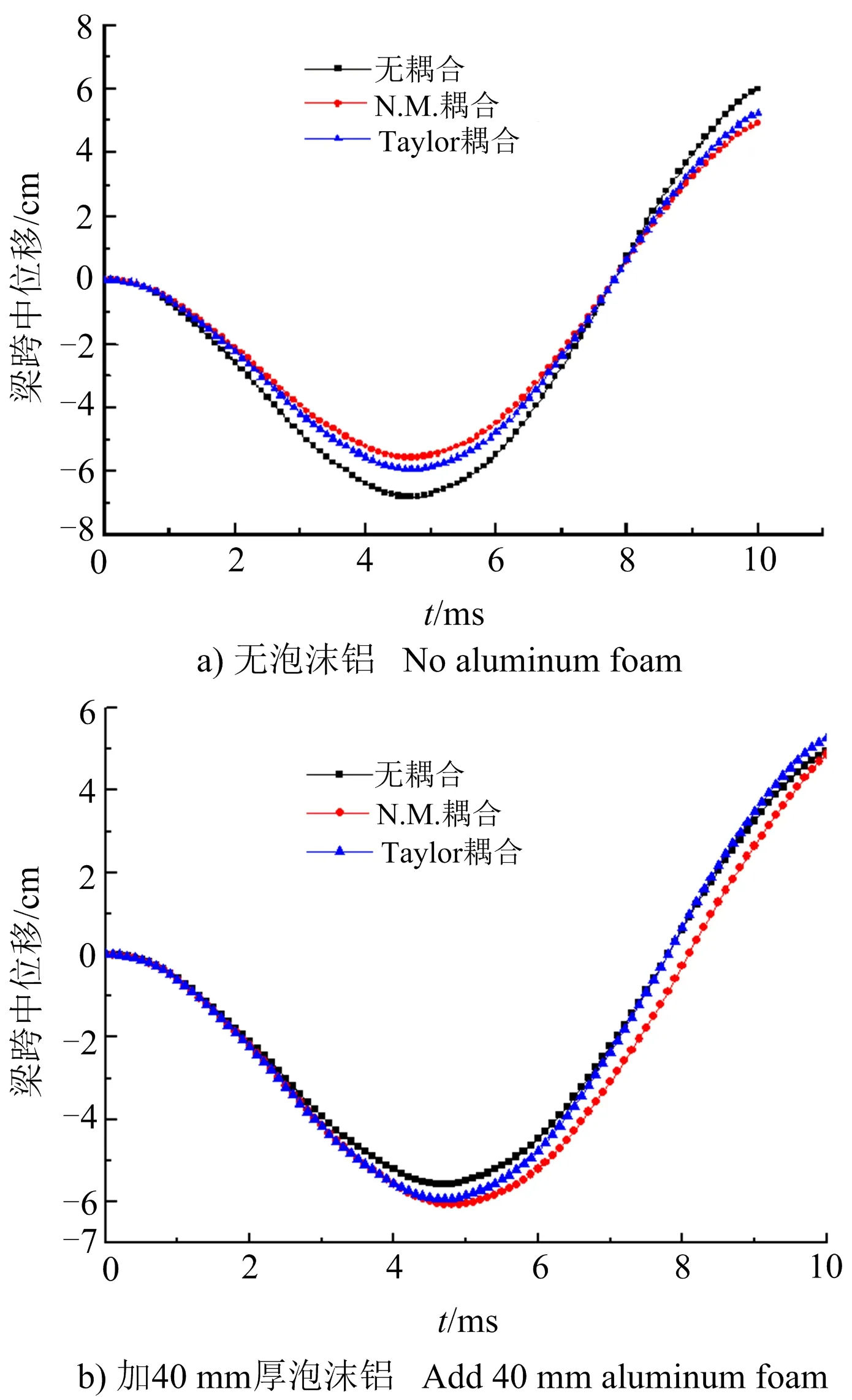
图7 有无FSI效应梁跨中位移计算结果对比Fig.7 Comparisons of calculation results of mid-span displacement of beams with or without FSI effect

2.2 泡沫铝厚度对衰减钢梁动态响应影响

由爆炸荷载作用下，包覆不同厚度泡沫铝后钢梁跨中位移时程曲线(见图8)可以看出，在泡沫铝屈服强度为3 MPa条件下，泡沫铝厚度越厚，对爆炸荷载的衰减效果越好。当泡沫铝厚度为80 mm时，可将梁跨中的最大位移衰减至未包覆泡沫铝时位移的71%，衰减效果明显。而泡沫铝厚度40 mm时，将梁跨中位移最大值由6.8 mm衰减至6.0 mm，衰减11%。随着泡沫铝厚度增加，相同条件下泡沫铝被压实的体积越大，吸收的能量也越多。从而对钢梁跨中最大动位移衰减也越多，符合能量守恒的基本逻辑。

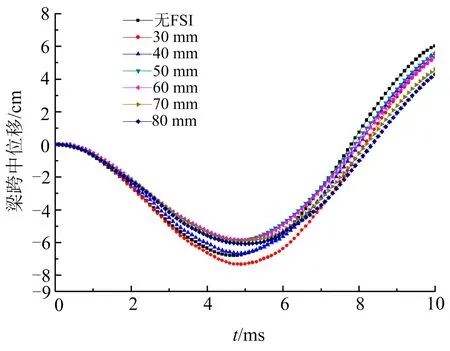
图8 泡沫铝厚度对衰减梁动力响应的影响Fig.8 Influence of aluminum foam thickness on dynamic response of steel beam

同时，从图8可以看出，当泡沫铝厚度增加至一定厚度后，其对钢梁在爆炸荷载下动力响应的衰减效应与厚度增加不成比例。厚度为50 mm的泡沫铝衰减效能与厚度为80 mm的泡沫铝衰减效果差值不到5%，在工程中这种差异可以忽略。

2.3 材料屈服强度的影响

泡沫铝屈服强度分别为3 MPa和21 MPa，厚度分别为40 mm与80 mm时，梁跨中位移时程曲线对比如图9所示。厚度与泡沫铝衰减梁动力响应具有正相关性，而同时，泡沫铝屈服强度也和其衰减钢梁的动力响应效果成正比。泡沫铝强度越高，则包覆泡沫铝钢梁在爆炸荷载作用下的跨中位移响应越小。对于实际工程应用，如何做到经济性的同时又满足衰减的要求是下一步研究工作的重点问题。

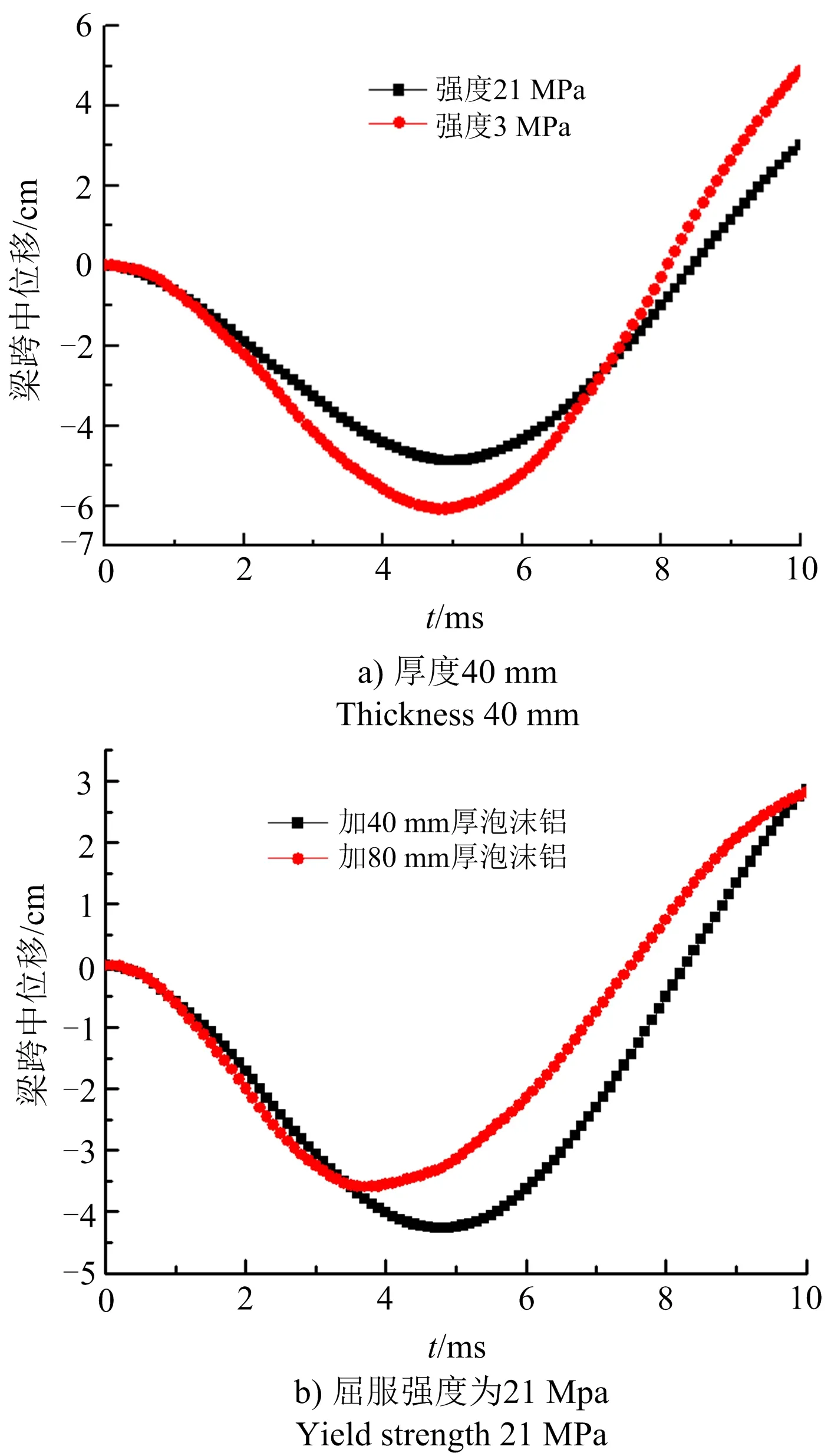
图9 不同屈服强度、不同厚度泡沫铝梁跨中位移时程Fig.9 Time history of mid span displacement of beams coated aluminum foam with different yield strength and thickness

泡沫铝厚度为40 mm，屈服强度对泡沫铝衰减梁动态响应的影响如图10所示。可以看出，随着泡沫铝屈服强度增加，梁跨中动态位移最大值相应减小，说明泡沫铝屈服强度的增加，在相同厚度下衰减性能更好。同时也发现在屈服强度增加的过程中有微小的变化。由图10b中直线的斜率可以明显看出，该条件下存在最优屈服强度范围。简言之，在给定条件下，在泡沫铝厚度一定下，存在一个最优的泡沫铝屈服强度对应最大可能衰减钢梁的跨中动态变形值。使得缓冲吸能设计取得最优效果。当泡沫铝屈服强度变化处于这个最优区间外时，其对钢梁具有一定的缓冲吸能效果，但效果不佳。如果将泡沫铝屈服强度调整到这个最优区间，就可以取得更好的衰减效果，达到节省材料与经济的良好局面，而在这个区间外变化泡沫铝屈服强度时，虽有影响，但效果一般。

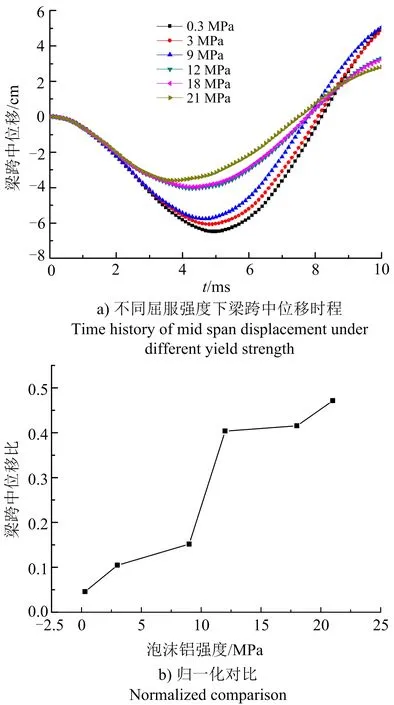
图10 屈服强度对泡沫铝衰减梁动力响应的影响Fig.10 Influence of aluminum foam yield stress on dynamic response of steel beam

3 结论

1)运用FSI理论可以考虑结构包覆泡沫铝对结构动力响应的影响，但FSI也有其局限性，其对包覆材料的厚度、屈服强度、结构刚度等因素的影响无法考虑。

2)增加包覆泡沫铝材料的厚度，可以提高其对爆炸荷载作用下钢梁动力响应的衰减效果，但当厚度增加到某一范围以上时，厚度增加的效果已经趋于稳定，再增加厚度提高的衰减效能有限。

3)泡沫铝的屈服强度越高，相同厚度泡沫铝对钢梁动力响应衰减效能越好，这符合能量吸收的相关理论。