基于遗传算法的巡检机器人路径规划算法的研究

徐国生，徐祖永，周俊杰，张皖军，邵珠鹏

(1.国家电投江西电力有限公司，江西 南昌 330096)

(2.国家电投集团信息技术有限公司，北京 100080)

为了解决人工巡检工作效率低、存在安全隐患等问题，无人值守的机器人开始走入大众视野。对于电力行业而言，智能电网的迅速发展促使机器人巡检逐步取代人工巡检，以减少危险工况环境对人员的安全威胁以及提高工作效率等。巡检机器人工作在复杂环境中执行巡检任务，其路径规划成为了国内外研究的热点[1]。Qureshi[2]将粒子群优化算法应用于最佳路径寻优问题中，并通过两组实验获得了超出预期的结果；Osvald等[3]在传统的启发式算法求解最佳路径的基础上，引入花授粉算法来提升全局寻优的性能，经实验论证，该算法在有限的算子范围内，能够获得较高质量的最优解，但是随着算子数量的增加，性能出现了明显的下降；周风余等[4]采用Lagrange建模进行机器人避障算法的研究，运用动力学模型获得最佳的避障路径；王建元等[5]提出了使用图结构的路径建模法，并结合GIS(geographic information system)建立三维地图，使其具有较好的寻址能力，但选择最佳路径的能力稍差。本文在前人研究的基础上，提出了基于改进遗传算法的巡检机器人路径规划算法，在种群初始化阶段使用混沌算法降低算法陷入局部最优的概率，使用自适应策略优化交叉算子与变异算子，进一步提升算法的收敛速度、执行性能和求解质量，另外，针对遗传算法局部寻优能力差的问题，采用模拟退火算法强化其整体寻优能力。研究结果表明，与经典的路径选择算法相比，结合了模拟退火及混沌算法的遗传算法效率更高，搜索的路径质量更好，算法具有良好的表现力。

1 遗传算法

遗传算法的核心思想是在有限资源内通过遗传方式保持后代先进性的同时寻求最优。其以群体中的全部个体为对象，采用随机化技术在已编码的种群的参数空间内完成高效搜索。首先进行染色体种群初始化，然后选择适应度函数、应用交叉以及变异完成最优个体的选择、遗传，获得最优解。算法流程如图1所示。

图1 遗传算法流程

算法的主要步骤如下：

1)参数初始化。初始化种群的规模、数量、交叉以及变异的概率值，同时对遗传代数和结束条件以及整体种群进行初始化，明确种群编码方式。

2)设置种群内个体的适应度，选择恰当的适应度函数。

3)计算种群内每个个体的染色体适应度值，使用选择策略优胜劣汰，获得能进入到下一代的优秀个体。

4)对于被选中的个体，使用交叉概率完成优秀个体的横向交叉。

5)对于被选中的优良个体，使用变异概率完成优秀个体的变异更新。

6)判断是否满足遗传结束条件或者达到遗传代数，满足则终止运算，否则返回步骤4)重复迭代。

遗传算法的核心是参数的编码、群体初始化以及个体适应度函数和遗传控制参数的选择。

2 改进遗传算法的路径规划

2.1 种群编码

种群编码及参数编码就是把问题的可行性解转换为遗传算法的搜索空间。由于编码方式对交叉算子、变异算子的执行效率会产生较大影响[6]，而广泛使用的二进制编码方式存在无效解的情况，因此本文选择整数编码方式进行染色体编码，具体过程如下：使用n标识巡检点位并编码，依次标识为1,2,…,n，使用m标识巡检机器人的数量，巡检完成的点位使用0标识，使用整数编码方式完成的染色体编码串为{1，…,S1，0，…,S2}，其中Si代表巡检点位，由此可见种群编码串的长度为(m+n+1)。由染色体编码串可知，染色体中必然存在的从0点位到0点位之间的子路径，该路径即为机器人巡检起始位置到各个巡检点位的巡检路径。如染色体编码串{0,1,3,4,0,2,5,7,0,9,6,8,0}中，有3个巡检机器人完成了9个点位的巡检，对应的巡检路径如图2所示。

图2 巡检路径示意图

2.2 种群初始化

种群初始化主要是设置种群规模，规模设置得过小，寻找最优解过程中容易陷入局部最优，降低算法的整体性能和质量；规模设置得过大，则运算量会明显增加[7]。目前常用的初始化种群算法(随机初始化、启发式算法)存在典型染色体优良度不均衡以及群体可行性无法保证的问题，本文引入了混沌算法，发挥其优秀的全局迭代搜索能力，来扩大染色体的遍历范围，具体做法是使用混沌算法生成混沌序列编码并成为种群染色体。

混沌序列为大量的非线性的多变结构模式。使用Logistic映射函数生成混沌序列，如式(1)所示：

Yn+1=μYn(1-Yn)

(1)

式中：μ为控制序列变化的参数，为0～4的常量；Yn为对变量x的n次循环遍历值，为0～1的随机数。对应的混沌映射结构图如图3所示。

图3 混沌映射初始化

由图3可以发现，经过对x变量的600次循环遍历，Logistic映射将混沌空间向量映射为对称、整体稳定但局部不稳定的分布在0～1的相对均匀的解空间向量，从而在初始化种群阶段降低遗传算法陷入局部最优解的概率。

2.3 自适应策略优化遗传参数

由于遗传算法的收敛速度、执行性能和求解质量受交叉算子和变异算子的影响较大，本文采用自适应策略优化交叉算子与变异算子，选择合理的参数。

1)交叉算子选择流程。

交叉算子受交叉概率的影响，如果交叉概率设置小了，在进化初期即开始出现相对近似的适应度值，产生局部最优解；如果交叉概率设置过大，则会降低搜索能力。因此，本文采用自适应策略产生动态交叉概率来优化交叉算子。由于种群采用优胜劣汰的模式，因此适应度较高的个体需要降低交叉概率，减少其破坏度，相反地适应度低的个体需要提高其交叉概率。采用式(2)对种群中优良个体间的适应度进行标定：

(2)

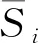
适应度函数Fi的计算公式为：

(3)

式中：Zi为成本；p为种群的规模。

在种群最初几代遗传过程中，由于种群的平均适应度值低，k值较小，进化接近尾声时，k值会增大到接近1，因此本文提出自适应交叉概率算法，如式(4)所示：

(4)

式中：Pc,f′,favg,Pmax分别为第i代种群交叉概率及其下限值、均值、上限值；Pc1(i)和Pc2(i)分别为第(i-1)代和第(i-2)代交叉概率。

自适应交叉概率算法流程如图4所示。

图4 自适应交叉概率算法流程

2)变异概率进化流程。

遗传算法通过变异算子参数增加种群的多样性，有效避免算法陷入局部最优解，若其值选择过大将会破坏优良个体，出现无最优解的情况，若其值过小，则会导致早熟[8-9]，因此本文提出自适应策略优化变异概率，既保持了种群的多样性，又避免了算法出现局部最优解的情况。具体计算公式如下：

(5)

式中：Pm，Pm1(i)，Pm2(i)分别为第i代种群变异概率及其上、下限值。

引入自适应策略的变异算子和交叉算子，可以适应性地调整种群遗传过程中的变化规律，保证优秀个体的传承，同时避免算法收敛过快以及局部最优等问题的出现。

2.4 改进遗传算法执行流程

为解决遗传算法局部寻优表现不足的问题，引入模拟退火算法，在遗传算法完成选择、交叉和变异操作的优选个体中，进行局部寻优，从空间深度获取最优解。

使用C代表当前的优选个体，Ti代表当前问题，P代表调整后的最新解，对应的目标函数为O，目标函数的增量使用Δf标识，模拟退火算法优化过程的metropolis准则[9-10]如公式(6)所示：

(6)

当Δf为负数时，则接受新解P，否则放弃新解。后续通过衰减率进行持续降温操作，直至获得最优解。

将模拟退火算法引入遗传算法获得巡检最佳路径的流程如图5所示。

图5 改进遗传算法的路径规划流程图

算法的具体步骤为：

1)初始化种群及模拟退火参数，包括种群规模p、模拟退火初始温度T、温降参数以及终止温度和迭代循环次数。

2)使用种群编码方式完成种群整体的初始化工作。

3)计算每个个体的适应度值。

4)执行优良个体选择操作，选择遗传到下一代的个体。

5)根据适应度标定动态调整概率进行变异和交叉操作，获得变异算子和交叉算子。

6)将优良个体引入模拟退火算法，计算个体新的适应度值，使用式(4)确认新的个体是否可以接受，如可接受则完成模拟退火算法的迭代，获得最优个体，输出最佳路径，否则重新执行步骤2)。

3 仿真与分析

3.1 路径规划仿真实验

为了验证本文提出的基于模拟退火和自适应策略改进的遗传算法规划机器人巡检最佳路径的性能，进行了仿真对比实验。仿真参数设置：种群规模为90，交叉概率的上、下限分别为0.51和0.84，变异概率的上、下限分别为0.04和0.20，最大迭代次数为500，模拟退火的初始温度为1 000 ℃，结束温度为100 ℃，温降系数为0.99。

本文进行了2组对比实验。首先与经典遗传算法进行对比，遗传算法的变异概率和交叉概率分别设为0.05和0.50，其他条件与本文算法一致。经典遗传算法的路径规划结果如图6所示，本文算法的路径规划结果如图7所示。

对比图6和图7可以发现，本文算法规划的路径最优路径的长度为6 581个单位长度，比经典遗传算法获得的最佳路径长度7 845个单位长度减少了264个单位长度，路径优化效果明显。

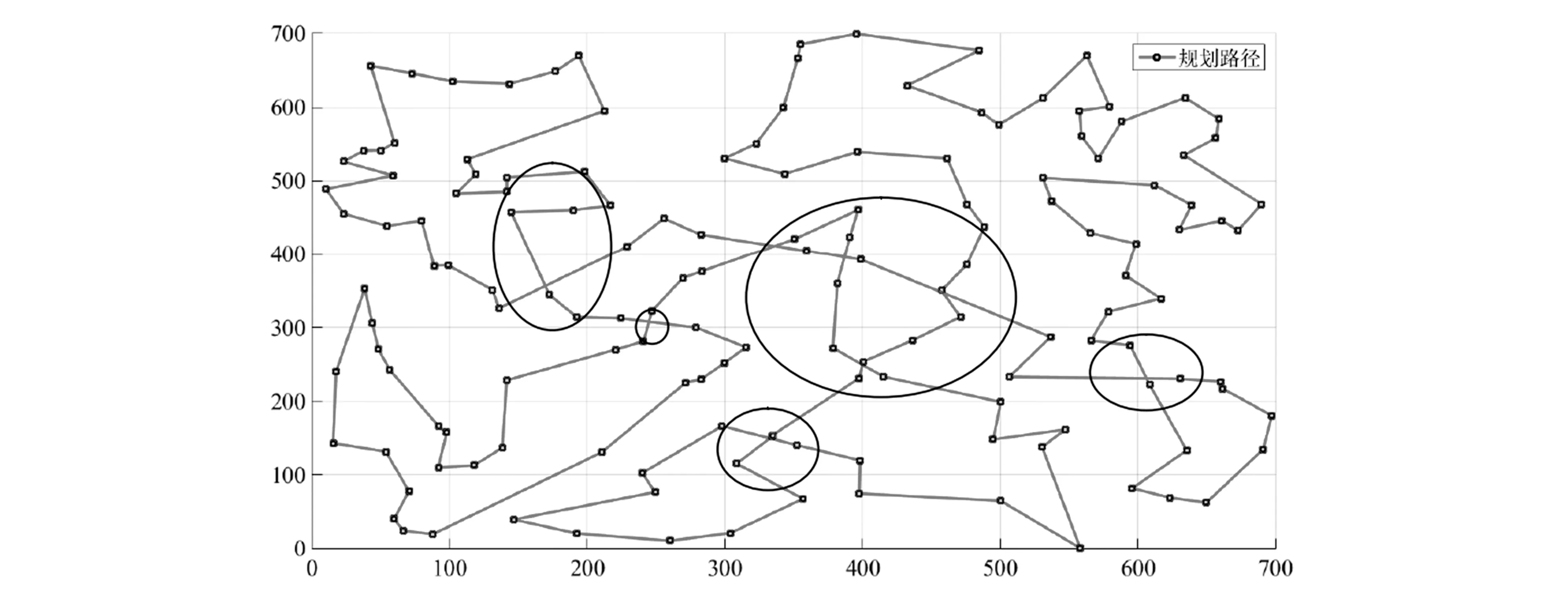
图6 遗传算法的路径规划图

图7 本文算法的规划路径

然后就算法的收敛速度分别与经典遗传算法、蚁群算法、模糊控制算法进行对比，共进行了2 000次仿真实验，平均搜索时间以及搜索成功率分别见表1和表2。由表可知，本文提出的算法在机器人路径规划中具有较快的收敛速度，准确率高，并且能以较大的概率收敛获得全局最优解，在复杂环境中体现得更加明显。

表1 本文算法与其他算法规划时间对比表 单位：s

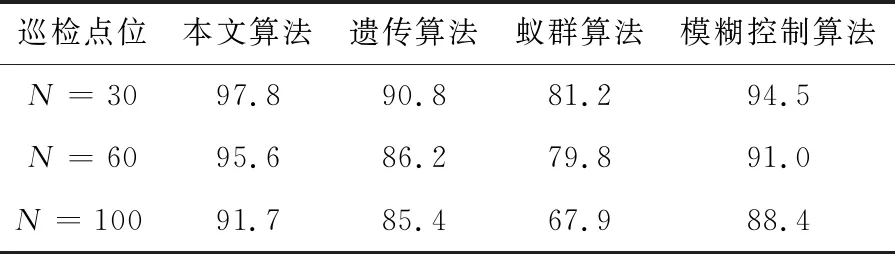
表2 本文算法与其他算法规划成功率对比表 %

3.2 机器人巡检应用

将本文提出的算法应用于电子地图进行仿真实验，人为设置模拟机器人从指定位置出发到1号主变压器所在的500 kV设备待检验区域(图8中的右上角框选部位，即为从1号主变压器到500 kV设备待检验区域)为最佳巡检路径。进行巡检点位编号，分别从机器人巡检开始的位置到巡检点按照一定规律编号，如图8所示。机器人初始位置设置为0号(图中箭头所示位置)，自左至右分别为1号、2号、3号，右边从下而上分别为4～8号，上方为9～12号，左边从下而上为13～18号。选择图8中的2号、15号和18号为巡检点位，完成规划后的路径将显示所有途径的点位。图8中标定的路径是本文算法规划的最佳路径，经过人工测量后符合最佳安全无障碍路径要求。经过多次试验，路径规划成功率可达100%。

图8 巡检地图

路径规划后，模拟机器人按照路径进行巡检，由于是单向巡检模式，因此在一侧巡检完毕后掉头巡检另一侧，按点位顺序的巡检路径为0 → 1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 12 → 11 → 10 → 9 → 13 → 14→ 15 → 16 → 17 → 18。巡检2号点位、15号点位和18号点位置的巡检路径分别为：路径1，0 → 1 → 2；路径2，2 → 3 → 4 → 5 → 6 → 7 → 8 → 12 → 11 → 10 → 9 → 13 → 14 → 15；路径3，15 → 16 → 17 → 18。

经多次运行验证，机器人的巡检结果与预计结果完全吻合。

4 结束语

为了提高机器人的巡检能力，满足智能电网无人化作业的要求，本文提出了基于模拟退火和自适应策略改进遗传算法的巡检机器人路径规划算法。以提升算法的寻优能力以及收敛速度为目标，在各个阶段分别使用混沌算法降低算法陷入局部最优的概率、自适应策略优化交叉算子与变异算子、使用模拟退火算法强化遗传算法整体寻优能力等，进一步提升算法的收敛速度、执行性能和求解质量。通过实验对比发现，本文提出的算法路径规划成功率比传统的遗传算法及蚁群算法平均提高了6%左右，巡检点数量在100以内时算法的执行时间平均在1 s左右，与其他算法相比性能有较大的提升，本文提出的算法具有较高的推广应用价值。