空气过滤器抗水雾性能试验台优化设计的数值模拟
张涛,刘道银,刘志坦,金默,周浩,付忠广
(1.华北电力大学能源动力与机械工程学院,北京,102206;2.国电科学技术研究院有限公司,江苏南京,210033;3.东南大学能源热转换及其过程测控教育部重点实验室,江苏南京,210096)
随着现代工业生产和科学实验活动等对环境洁净度要求的提高,空气过滤器的作用日益凸显,并在半导体生产、制药工业和工业空气处理等行业的空气动力设备中扮演着重要角色[1]。当空气过滤器在浓雾、雨水和高湿等自然气候条件下运行时,过滤器易发生压差急剧增长现象[2−3],严重影响设备运行的安全性和经济性。然而,当前国际上缺少过滤器抗水雾性能评价和测试方法,已有阻力、效率及容尘等评价指标无法满足过滤器工业应用的需求[4],因此,制定过滤器抗水雾性能测试评价方法具有重要的现实意义。本文作者提出过滤器抗水雾性能测试ISO 国际标准[5],同时开发用于测试过滤器抗水雾性能的标准试验装置。
众多学者对空气过滤器和液体喷雾装置性能进行了实验研究。林忠平等[6]根据现有欧洲标准[7]及中国制冷空调工业协会标准[8]搭建了空气过滤器测试装置,并测量多种过滤器及风机过滤单元进行效率、阻力以及容尘量[9];周刘轲等[10]对组合式空气过滤器与单体过滤器在一般通风试验台中进行了对比试验,发现组合式空气过滤器的阻力小于相同风量下相应单体空气过滤器阻力之和,单位面积容尘量是相应风量下单体空气过滤器计算和的数倍;蒋仲安等[11]通过实验分析了气液两相喷雾的雾化性能影响因素,并验证了喷嘴雾化最小粒径的存在;孙中圣等[12]通过试验研究了进出口压差、油膜厚度及油温等因素对气力式油雾器雾化性能的影响;苏明旭等[13]采用超声波声衰减颗粒测量方法开展了蒸汽液滴粒径和质量浓度的测量实验,拓展了液滴粒径测量方法;SUN等[5]研究了在一定水雾浓度下,过滤器安装位置、重复过滤次数以及载尘等因素对过滤器压降的影响,指出后续实验研究需要考虑相对湿度以及温度的影响,然而,这将显著提高后续实验成本与复杂程度。
近年来,数值模拟方法已广泛应用于研究过滤器性能优化和液滴运动领域。何志霞等[14]模拟研究了空气过滤器流动阻力和滤芯流动均匀性,并优化分析了其结构;黄乃金等[15]建立了滤芯三维拟态化结构模型,计算运行及结构参数对滤芯压力损失和过滤效率的影响;YANG 等[16]应用Euler-Lagrange方法模拟了室内环境下液滴输运及蒸发过程;ZHAO等[17]采用数值模拟方法研究了核电站安全壳喷淋系统中液滴运动和相变过程;XIAO 等[18]应用离散相模型,追踪液滴在单分散液滴喷雾干燥器中的运动情况;FLORIO 等[19]运用VOF(volume of fluid)方法模拟高温高压气体携带的铜液滴在钢管内的运动状态,并捕捉到了其变形、分裂与沉积过程;KHAN 等[20]运用LES(large eddy simulation)方法模拟室内非蒸发液滴的湍流运动过程,得到的结果与实验结果相匹配;ZHANG 等[21]对单个液滴碰撞干燥/湿润壁面后的破碎飞溅现象进行了数值模拟,总结了不同壁面条件下的临界液滴破碎数;PAWAR 等[22]通过模拟高压喷嘴出口处高速液滴之间相互作用,得到了液滴旋转速度、喷射宽度与液滴粒径分布等参数。
本文在开发过滤器抗水雾性能标准试验台的背景下,采用数值模拟的方法研究试验台管道内的雾化水液滴的运动和捕集过程,分析比较不同条件下雾化液滴从管道入口到达空气过滤器入口处的液滴浓度与粒径的变化规律,以期为设计过滤器抗水雾性能标准实验台提供理论依据,为空气过滤器抗水雾性能评价体系提供数据支撑。
1 数学模型
1.1 液滴运动过程物理模型
为了减小外界环境温度和湿度对管道中水雾性能的影响,在拟设计的整个试验系统中采用循环风管道,空气流出管道后再通过循环风管道返回管道进口,因此,在进口处喷入一定量的水雾后,可维持系统中工作介质为饱和湿空气。
标准试验台主体管道的几何模型如图1所示。由图1可见:饱和湿空气由管道入口处进入,液滴由位于管道入口面中心处的喷嘴喷出。液滴伴随饱和湿空气在管道中运动,部分液滴发生碰撞,进而发生聚并或破碎。部分液滴与壁面发生碰撞并被壁面捕集;由于管道中的空气处于湿饱和状态,由蒸发而造成的液滴损失可忽略不计,其余液滴将会运动到达过滤器(受试件)入口面,通过过滤器离开管道。
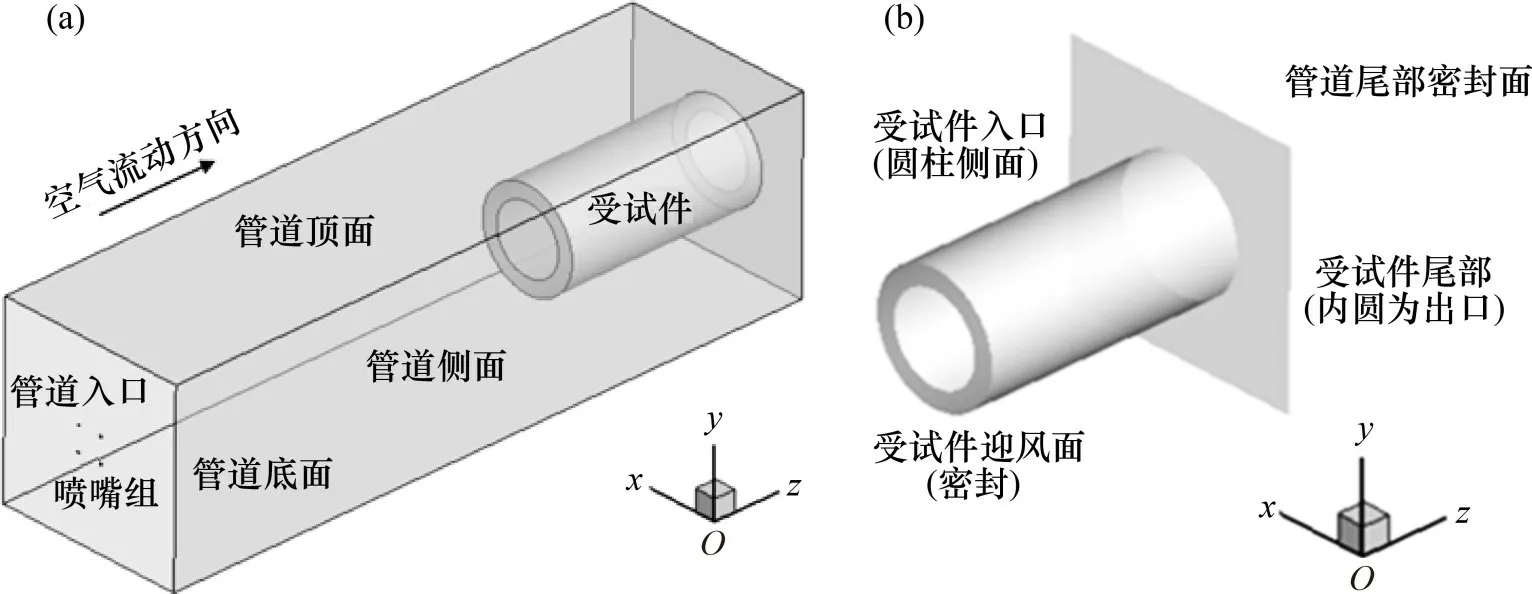
图1 管道几何模型Fig.1 Geometry model of pipe
1.2 湿空气流动模型
管道内饱和湿空气的运动采用标准k−ε湍流模型进行计算。在标准k−ε模型中,动能k和湍动能耗散率ε的守恒方程如下:
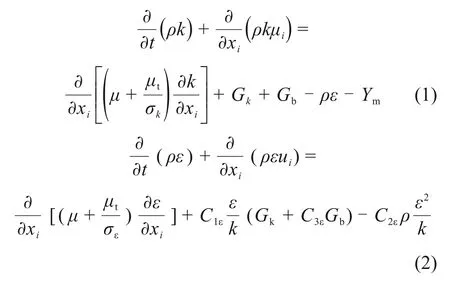
式中:ρ为流体密度;k为湍动能;Gk为平均速度梯度所产生的湍动能;Gb为由浮力产生的湍动能;Ym为脉动扩张对总体耗散率的贡献;σk和σε分别为湍动能与耗散率的普朗特数。相关参数取默认值,C1ε=1.44,C2ε=1.92,σk=1.3,σε=1.0。对应地,湍流黏度μt计算式如下:

式中:Cμ取经验值0.09。
1.3 液滴运动模型和碰撞破碎模型
在离散相模型中,采用随机碰撞模型、聚并模型以及Wave 破碎模型[23]追踪液滴的运动、碰撞和破碎。离散相液滴运动轨迹根据其受力平衡计算:
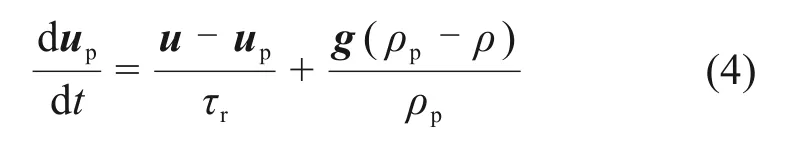
式中:u和up分别为流体速度和颗粒速度;τr液滴松弛时间;ρp为颗粒密度;g为重力加速度。液滴松弛时间τr计算式如下:
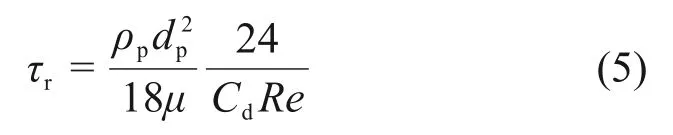
式中:dp为液滴直径;Cd为流体曳力系数;μ为流体黏度;Re为雷诺数。
在随机碰撞模型中,液滴间的碰撞概率P1为
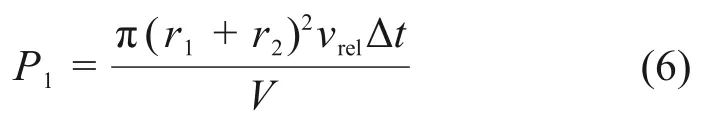
式中:V为连续相网格单元体积;r为液滴粒径,下角标1 和2 分别表示碰撞中较大液滴和较小液滴;Δt为时间步长,vrel为小液滴相对于大液滴的速度。
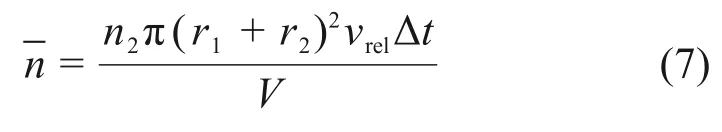
实际液滴碰撞数目概率分布服从泊松分布P(n):
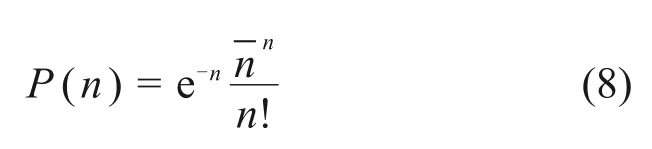
液滴是否发生聚并取决于实际碰撞参数b与标准碰撞参数bcrit,计算式如下:
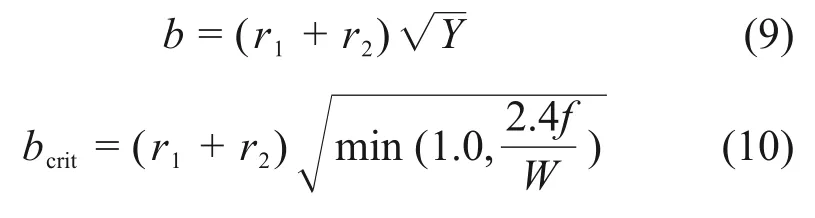
式中:Y为0 到1 之间的随机数;W为韦伯数。W的计算式如下:

式中:v为特征速度;l为特征长度;σ为流体表面张力。
在式(10)中f是关于碰撞液滴粒径比r1/r2的方程,定义为
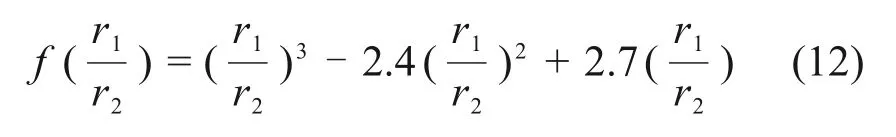
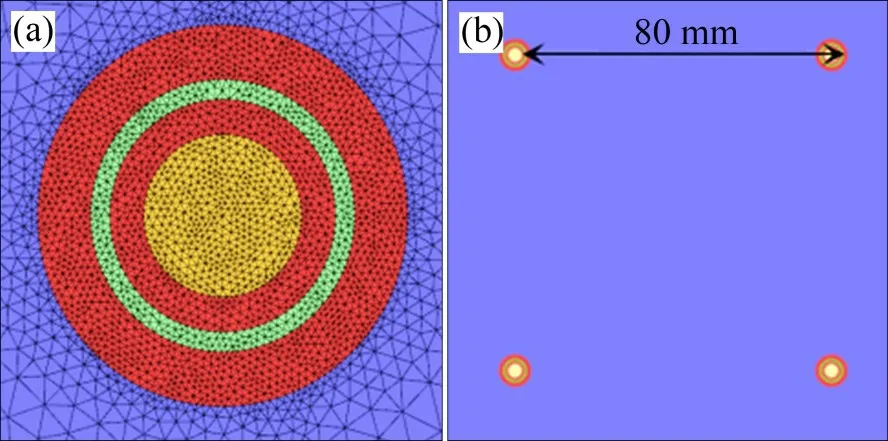
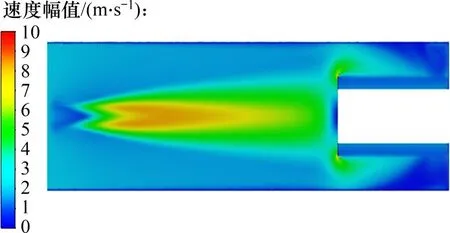
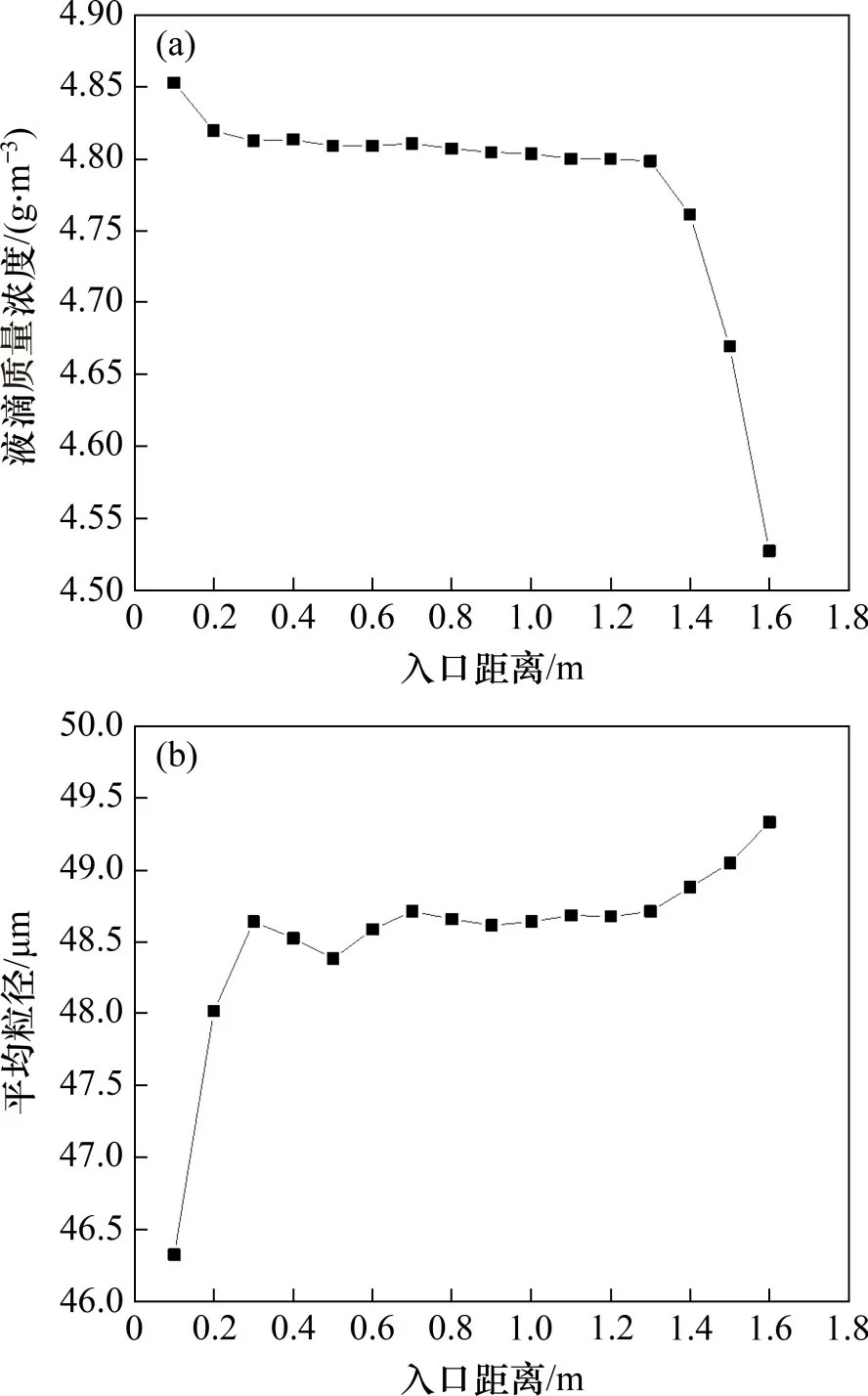
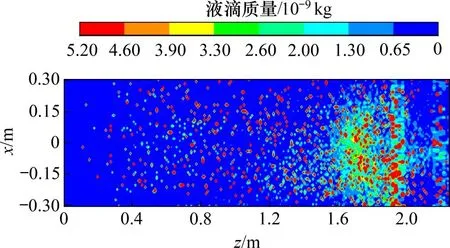
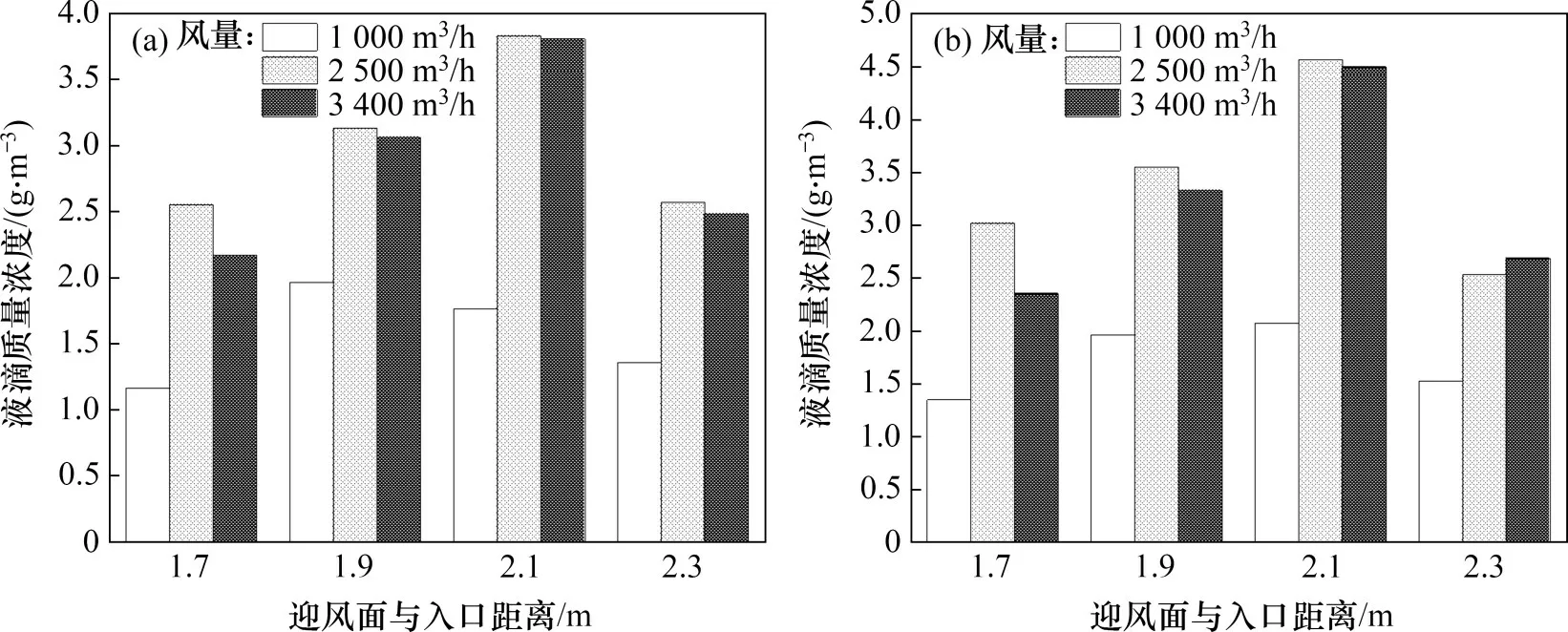
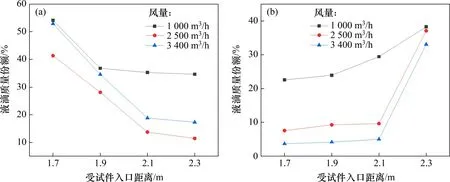
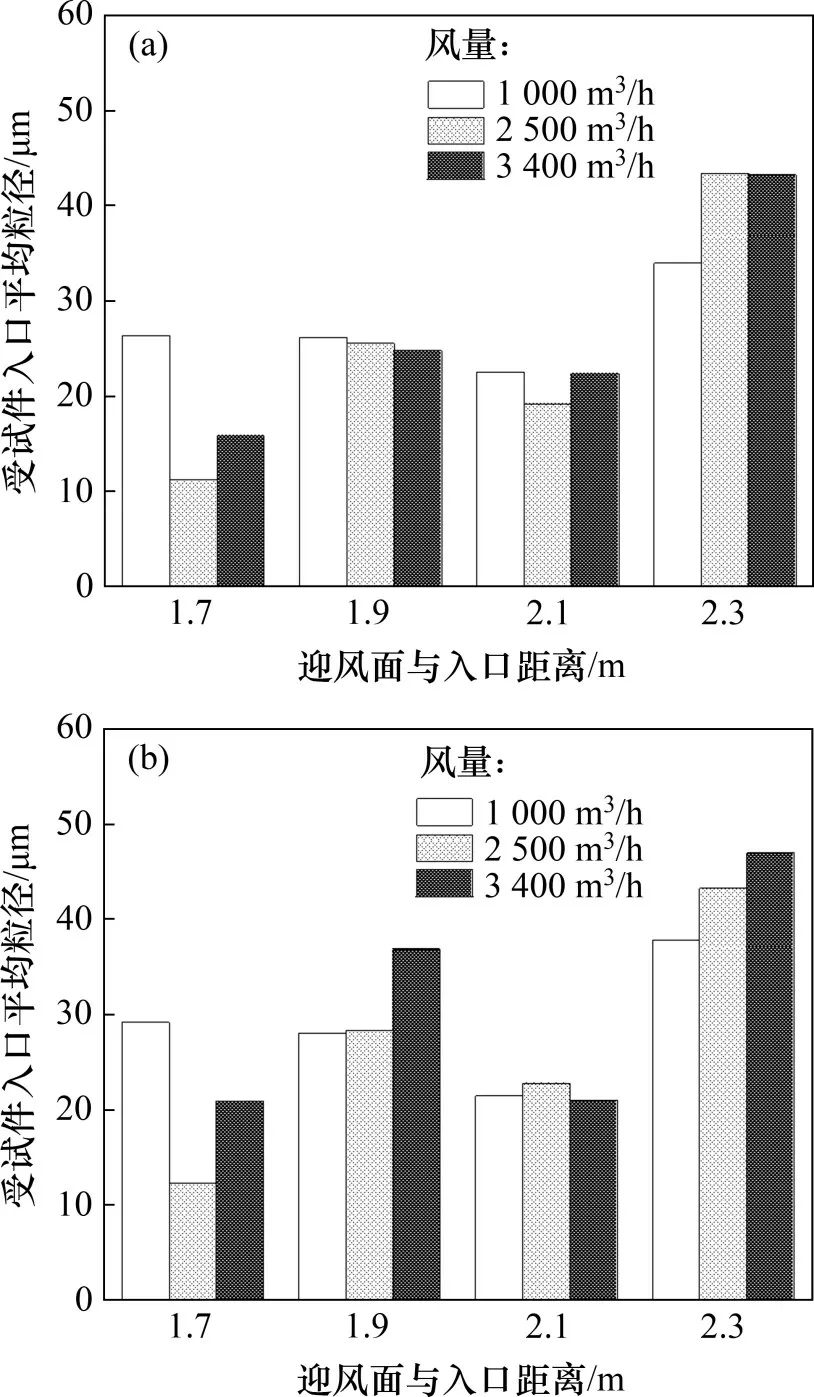
若b 由于管道中液滴运动速度较快,经过估算,韦伯数W>100,需要考虑颗粒的破碎现象,所以,采用Wave 破碎模型。在Wave 破碎模型中,液滴的破碎是由液滴与气体间相对速度引起的。模型中假设破碎时间与破碎形成液滴的直径由快速增长的Kelvin-Helmholtz 不稳定性决定,而Kelvin-Helmholtz 不稳定性的波长与增长率用于预测新形成液滴的性质。新形成的液滴粒径r为 式中:B0取常数0.61;Λ为波长。 液滴破碎时间τ由以下式计算: 式中:B1根据聚团情况,取1~60 之间的常数;Ω为最大成长速度, 波长Λ的计算公式为 式中:Oh=Wg0.5/Re,为奥内佐格数;Ta=Oh·Wl0.5,为泰勒数;Wg和Wl分别代表气相和液相的韦伯数。 根据空气过滤器抗水雾性能测试试验台的尺寸,采用ANSYS ICEM CFD 软件进行几何建模。模型外观为正方形管道,内截面边长为610 mm;受试件为空心圆柱体,长度为650 mm,内圆直径为220 mm,外圆直径为320 mm,过滤层厚度为50 mm,圆柱体放置于管道出口中心处。管道入口截面设置4个雾化喷嘴。具体布置如图1所示。 为了确定合理的管道长度,受试件迎风面与管道入口的距离可以调节,分别取1 700,1 900,2 100 和2 300 mm,对应的总管道长度分别为2 350,2 550,2 750 和2 950 mm。在管道入口截面布置4个喷嘴,喷嘴的间距为80 mm。选用双流体喷嘴,内圆通液体,外环通压缩空气,单个雾化喷嘴的内圆直径3.50 mm,外环直径分别为5.00 mm 和5.85 mm,喷嘴附近加密网格及多喷嘴布置情况如图2所示。 图2 喷嘴附近加密网格以及喷嘴组布置Fig.2 Refined grid near nozzle and nozzle group layout 计算域网格采用四面体非结构化网格,在喷嘴局部处加密,网格总数为120 万个左右。采用ANSYS Fluent v16.0软件进行计算,先进行连续相的计算。当连续相计算结果收敛后,再进行离散相计算,液滴释放总时长为3 s。 管道入口面为气体入口,进口速度分别取0.747,1.870 和2.540 m/s(对应风量分别为1 000,2 500和3 400 m3/h)。入口流体为300 K的饱和湿空气,相对湿度为100%,其中水蒸气质量分数w(H2O)=0.022 8,氧气质量分数w(O2)=0.252 3,氮气质量分数w(N2)=0.724 9。整体计算域为:x方向(−305,305) mm,y方向(−305,305) mm,z方向(0,L)mm。L为管道总长度,分别取2 350,2 550,2 750和2 950 mm。 雾化喷嘴内圆为液滴释放面,初始液滴粒径分布采用Rosin-Rammler 分布,最小粒径为5 μm,最大粒径为50 μm,Rosin-Rammler 分布的平均粒径为20 μm。 雾化喷嘴外环为压缩空气入口,进口速度为200 m/s。入口流体为300 K的饱和湿空气,水蒸气质量分数与氧气质量分数设置与入口处的相同。 受试件出口面为压力出口,压力为0 Pa(下文如无特殊说明,均为表压)。 受试件按照多孔材料设置,依据渗流二项式定律计算其阻力系数。流动方向黏性阻力系数为2×106,惯性阻力系数为700,其余2个方向黏性阻力系数为2×107,惯性阻力系数为7 000,孔隙率为0.4。在1 000,2 500和3 400 m3/h的风量下,对应的受试件阻力分别为110,350和580 Pa。 模拟研究了风量、初始入口液滴浓度、入口与受试件迎风面之间的距离对液滴运动的影响。风量分别取1 000,2 500 和3 400 m3/h,初始入口液滴质量浓度分别取5 g/m3和6 g/m3,入口距离受试件迎风面分别取1.7,1.9,2.1和2.3 m。 不同风量以及受试件迎风面与入口距离下管道内流场分布类似,仅在数值上有所区别。下面以1个典型工况为例,分析流场和液滴运动的合理性。当风量为1 000 m3/h,初始入口液滴质量浓度为5 g/m3,入口距离受试件迎风面1.7 m 时,管道YZ截面速度幅值云图如图3所示。由图3可见:由雾化喷嘴引起的中心射流的影响一直延伸至受试件迎风面,受试件侧面气体速度基本均匀,表明受试件的放置位置基本合理。 图3 截面流体速度幅值云图Fig.3 Contour of fluid velocity magnitude 在该工况下,液滴质量浓度和液滴平均粒径沿管道轴向的变化规律如图4所示。如图4可见:沿管道方向,液滴粒径整体呈增加趋势,这是在运动过程中液滴碰撞聚并引起的;而液滴质量浓度呈降低趋势,这是液滴碰到壁面被捕获引起的;当到达受试件迎风面时,液滴质量浓度会急剧下降,这是流场受到受试件阻拦所致,部分液滴被挤向管道壁面从而被捕获。 图4 液滴质量浓度与平均粒径沿距离变化Fig.4 Variation of mass concentration and mean diameter of droplet diameter along distance 同时,模拟分析了液滴在管道流程不同位置的质量分数(不同位置处捕捉的液滴质量与喷雾总质量之比)以及到达受试件入口的比例,可知质量分数超过54.1%的液滴被受试件迎风面捕集,23.3%被受试件拦截,沉积在管道底面的质量分数为11.4%,到达受试件入口的质量分数为23.3%,而管道其余壁面捕集的液滴质量分数较小。其中管道底面捕集的液滴质量分布如图5所示,由图5可知,随着液滴运动距离增加,底面捕集液滴质量逐渐增加,且在受试件(z=1.7 m)附近液滴被底面捕集的量有明显提升。 图5 管道底面捕集的液滴质量分布Fig.5 Mass distribution of droplets captured on bottom of pipe 部分液滴在管道内的运动轨迹如图6所示。从图6可见:在1 000 m3/h 的风量下,液滴的运动轨迹较发散,部分液滴在受试件上游便被管道壁面捕捉,同时也有较多液滴被受试件迎风面捕集;当到达受试件迎风面时,由于流场受到受试件阻拦,气流中液滴质量浓度会急剧下降。 图6 部分液滴运动轨迹图Fig.6 Typical trajectories of a fraction of droplets 受试件入口处液滴质量浓度是衡量过滤器抗水雾性能试验中的重要参数。在不同风量、受试件迎风面与入口之间距离和初始入口液滴质量浓度下,受试件入口处液滴质量浓度变化如图7所示。从图7可见:在3种风量条件中,整体上风量为2 500 m3/h 时受试件入口处液滴质量浓度最高,而风量为1 000 m3/h 时液滴质量浓度最低。在2 500 m3/h 和3 400 m3/h 风量下液滴质量浓度随受试件迎风面与入口处距离增加而变化的规律相同,即当距离由1.7 m 提升至2.1 m 时,液滴质量浓度逐渐提升,但当距离提升至2.3 m时,液滴质量浓度则出现了明显下降;当初始入口液滴质量浓度由5 g/m3提升至6 g/m3时,对应工况下液滴质量浓度有所提升,而液滴质量浓度随风量和距离变化而变化的规律大体一致。 图7 不同风量和距离下受试件入口处液滴质量浓度Fig.7 Droplet mass concentration at the entrance of test piece under different distances and air flow rates 造成以上现象的原因可从液滴运动过程中的被受试件迎风面和管道壁面的捕集质量分数加以分析,如图8所示。从图8可见:在相同的受试件与入口距离下,3 400 m3/h 风量下受试件迎风面捕集液滴质量分数比2 500 m3/h风量下的质量分数的高,而管道壁面捕集的液滴质量分数则随风量提升而下降。这是由于在风量较大的情况下,相同液滴能在被管道壁面捕集前沿湿空气流动方向运动更长距离从而更易进入受试件,且由于自身惯性力提升,液滴更倾向于保持原有的运动轨迹而与受试件迎风面发生碰撞。在相同风量下,被受试件迎风面捕集的液滴质量分数随受试件与入口距离提升而下降,而被管道壁面捕集的液滴质量分数随受试件与入口距离的提升而提升,且当距离由2.1 m 提升至2.3 m 时提升幅度最高。造成这种现象的原因可结合图3、图5以及图6加以分析,液滴的运动轨迹将随自身的运动距离提升而在管道内充分发展并被管道壁面捕集,且在重力作用下,液滴沿湿空气流动方向运动距离越长,越容易被管道底面捕集。 图8 不同风量和距离下液滴被捕集的质量份额Fig.8 Mass fraction of droplets collected under different air flow rates and distances 除受试件入口处液滴质量浓度外,受试件入口处液滴粒径也直接影响水雾性能。在不同风量、受试件迎风面与入口之间距离和初始入口液滴质量浓度下,受试件入口处液滴质量浓度变化如图9所示。从图9可见:在相同风量下,液滴平均粒径大体上随受试件迎风面与入口距离增加而增加,但距离2.1 m 时液滴平均粒径低于距离为1.9 m 的液滴平均粒径;当初始入口液滴质量浓度由5 g/m3提升至6 g/m3时,对应工况下液滴平均粒径不同程度提升,平均粒径随风量增加而变化规律大体一致;风量和受试件入口处液滴平均粒径之间缺乏相关性,主要体现在不同受试件迎风面与入口距离以及初始入口液滴质量浓度下,不同风量下液滴平均粒径关系并不统一。 图9 不同距离下受试件入口处液滴平均粒径Fig.9 Droplet mean diameter at the entrance of test filter under different distances 在受试件迎风面与入口距离为2.1 m时,液滴平均粒径的变化情况可通过分析受试件入口处液滴粒径分布进行解释,如图10所示。从图10可见:在风量为2 500 m3/h,初始入口液滴质量浓度为5 g/m3的工况下,在距离为1.9,2.1 和2.3 m 时,液滴粒径分布范围大体一致,均为0~150 μm,但在距离为2.1 m 时,粒度低于60 μm 的液滴质量分数明显高于1.9 m 和2.3 m 时的质量分数,因此,导致该距离下液滴平均粒径较小。 1)采用数值模拟研究空气过滤器抗水雾性能测试实验台液滴运动特性,获得雾化水液滴典型运动轨迹以及到达空气过滤器入口处液滴质量浓度和粒径的变化规律,可为空气过滤器抗水雾性能测试标准制定提供数据支撑。 2)整体上管道内液滴质量浓度随运动距离增加而减少,且在靠近过滤器时减少明显,液滴平均粒径随距离增加而增加。 3)过滤器迎风面以及管道底面捕集的液滴质量分数相对较高。管道底面捕集的液滴质量分数随风量增加而降低,随过滤器迎风面与管道入口距离增加而增加,且在过滤器附近区域有明显提升。过滤器迎风面捕集的液滴质量分数随风量增加而增加,随过滤器迎风面与管道入口距离增加而降低。 4)过滤器入口处液滴质量浓度变化规律与液滴平均粒径的变化规律相似,整体上随过滤器迎风面与管道入口距离和初始液滴质量浓度增加而增加。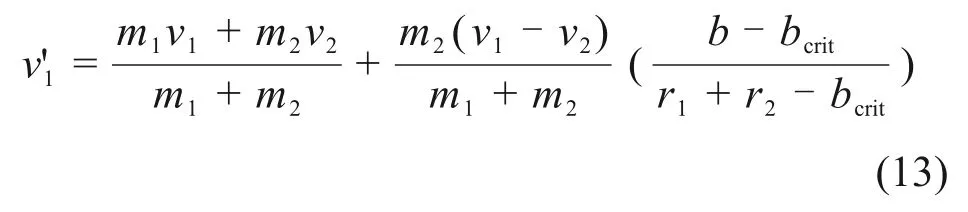

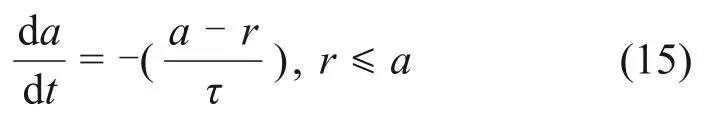
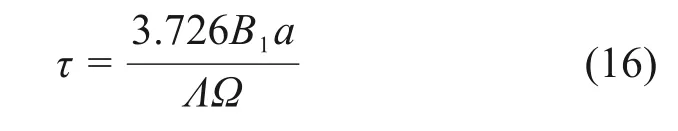
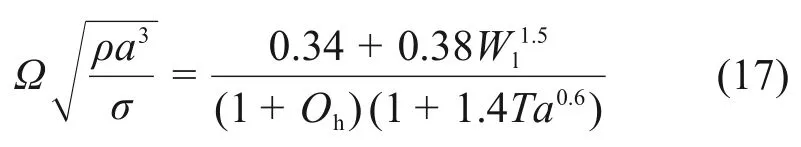
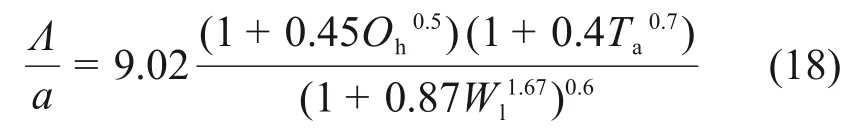
2 液滴运动过程的计算方法
2.1 几何模型与网格生成
2.2 边界条件
3 结果与分析
3.1 特征工况下液滴沿管道运动情况

3.2 受试件入口液滴质量浓度变化
3.3 受试件入口处液滴粒径的变化
4 结论

