微通道冷却非均匀热流密度芯片的流动换热特性

申利梅，季俊杰，罗凡，陈建业，谢军龙，黄涛

(1.华中科技大学能源与动力工程学院，湖北武汉，430074；2.中国烟草总公司湖南省公司，湖南长沙，410004)

随着电子技术的飞速发展，微型化、高集成的大功率电子器件得到广泛应用。1965年，英特尔联合创始人戈登.摩尔提出了著名的摩尔定律[1]，即单个芯片上集成的晶体管数量每18～24个月就会翻一番。单位面积上集成器件数量增多将导致芯片热流密度大幅提高。芯片过高的热流密度将导致器件温度超过其正常工作温度范围，从而加速电极劣化，降低使用寿命，甚至无法正常工作[2]。过增元[3]指出电子芯片温度在70～80 ℃的水平上每增加1 ℃，其可靠性将下降5%。因此，电子器件的热管理成为限制其发展的重要因素。微通道液体冷却技术由TUCKERMAN 等[4]提出后，因其较高的冷却热流密度(790 W/cm2)而受到广泛关注。

受微尺度效应及其他因素影响，微通道内的两相流型与常规尺寸通道相比有很大差异[5]，常规通道下的流动换热特性对于微通道已经不再适用。微通道中的两相流型对于探求其流动换热特性有重要意义，学者们发现在不同质量流速、热流密度和蒸发压力等条件工况下，微通道内出现的两相流型有所不同。SAISORN等[6]实验观察了R134a在圆形通道内的两相流型，在热流密度为0.1～8.3 W/cm2，质量流量为200～1 000 kg/(m2·s)，饱和压力分别为0.8，1.0 和1.3 MPa 的工况下发现了5种不同的流型，即弹状流、喉−环形流、搅拌流、环形流和小环形流；YANG 等[7]实验研究了R134a在矩形单通道内的两相流动换热，发现在热流密度为0.091 8～0.699 3 W/cm2，质量流量为1821～4115 kg/(m2·s)的工况下的流型包括泡状流、弹状流、搅拌流和环形流；THIANGTHAM 等[8]研究热流密度为4～12 W/cm2，饱和温度分别为13，18 和23 ℃，质量流量分别为150，400 和600 kg/(m2·s)的实验工况，发现R134a在矩形多通道内出现了泡状流、泡状−弹状流、弹状流、塞状流、波浪环形流以及光滑环形流。总结文献[6−10]发现，当流型处于泡状流和弹状流等初始沸腾阶段，受相变潜热以及气泡扰动影响，较高热流密度能在一定程度上提高微通道换热能力，而进一步提高热流密度使流型转换成环形流时，则极易出现蒸干现象，导致壁面温度骤升。

除流型外，微通道内的流动换热特性还受热流密度和质量流量等因素影响，研究者从这些方面研究微通道冷却技术，存在较大分歧。SAITOH等[11]认为低干度区核态沸腾是主要换热机制，高干度区则转换为对流沸腾占主导；TRAN等[12]认为微通道内两相流动换热系数取决于热流密度，与质量流量无关；YUN 等[13]则提出用韦伯数W区分热流密度和质量流量对换热系数的影响，当W<100时，热流密度对换热系数的影响较大，当W>100时，换热系数则主要取决于质量流量。对于压降的研究结论较统一[14−17]，即质量流量对压降的影响显著，质量流量越大，两相压降越大；随着热流密度增大，液体工质蒸发引起干度增大，压降随着干度增加而上升。

综上所述，目前关于微通道流动换热特性研究大多是基于均匀热流密度的工况。但对于实际的芯片冷却，其热流密度是非均匀的。MAGANTI等[18]研究了微通道冷却Intel®Core™i7芯片，发现存在严重的温度分布不均匀问题，其表面最大温差可达40 ℃，并指出这是由于微通道流体分配和热点分布不均引起的；ANSARI等[19]设计了一种板翅−针翅组合式的微通道，当用于冷却背景热流密度为50 W/cm2和热点热流密度为300 W/cm2的芯片时，相对于板翅式微通道，可使芯片表面最大温差由50 ℃降到30 ℃。

为了进一步研究热点对微通道冷却芯片的影响，本文作者采用VOF(volume of fluid)方法，建立微通道冷却非均匀热流密度的二维相变仿真模型，研究局部高热密度热点作用下微通道内的流型转换以及流动沸腾换热特性，分析影响温度均匀性的因素，从而指导微通道优化。

1 数值方法

1.1 物理模型

研究的微通道类型为矩形直通道，考虑到通道结构的对称性，并结合计算资源和数值模拟的要求，将三维微通道简化为二维(暂不考虑宽度方向的变化)。微通道主要结构参数如图1所示，矩形的长度为10.0 mm，高度为0.2 mm，上表面绝热，下壁面为加热表面，且为划分出热点区域将下壁面分为3个部分，左右两侧长度各4.9 mm，中间0.2 mm处为热点区域。

图1 微通道模型图Fig.1 Model diagram of micro-channel

计算模型采用结构化网格进行划分，并对仿真结果进行了网格无关性验证，确保其为网格无关解。以底面均匀热流密度为20 W/cm2，入口流速为0.5 m/s 边界条件下的底面平均温度进行网格无关性验证，结果如图2所示。

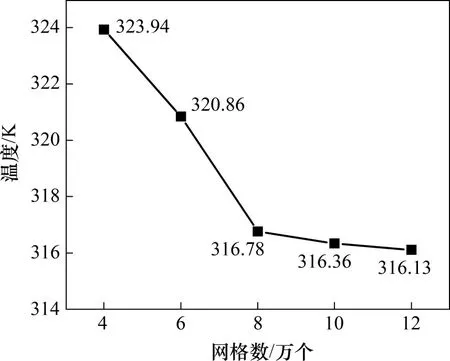
图2 网格无关性验证结果Fig.2 Result of grid independence verification

考虑到网格数量对计算速度和精度的影响，10 万的网格数量下其温度已基本恒定，达到仿真精度要求。将不同入口流速的工质在微通道内流动沸腾时的壁面平均换热系数与SUN 等[20]提出的经验公式进行对比，如图3所示，对比结果表明相对误差在5%以内，由此可验证模拟结果的准确性。

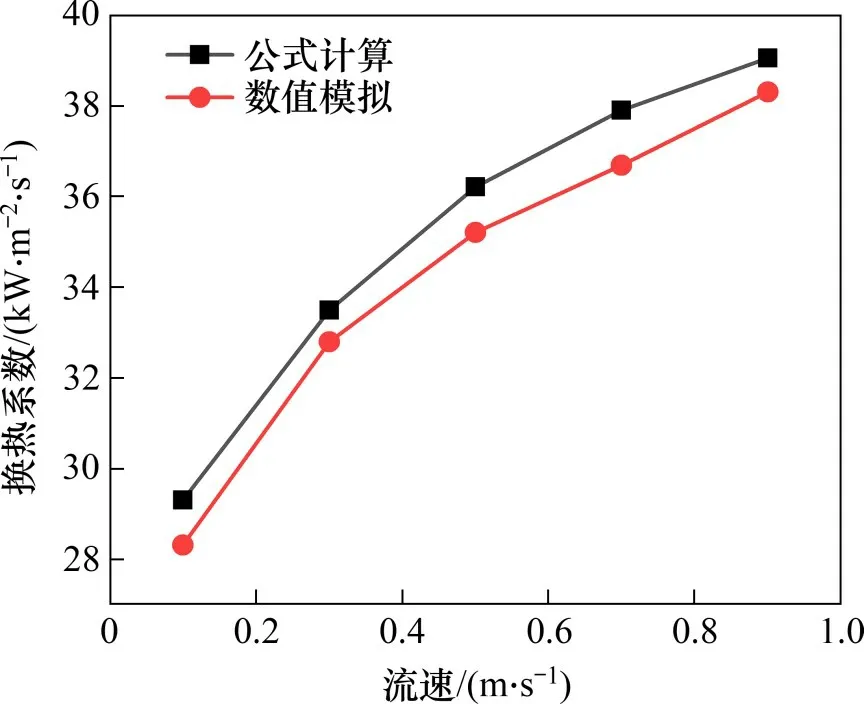
图3 壁面换热系数模拟结果与经验公式对比Fig.3 Simulation result of wall heat transfer coefficient compared with empirical formula

1.2 控制方程

VOF(volume of fluid)是一种在固定欧拉网格下追踪气液交界面的方法，通过求解一组动量方程并跟踪整个计算域中每种流体的体积分数对2种或2种以上不相溶流体进行仿真计算。本文采用VOF模型追踪计算域内工质的气液两相转变，并选用LEE 模型描述气液两相间的质量输运，该模型为基于气体动力学理论的传质相变模型。控制方程如式(1)～(4)所示。

质量方程：

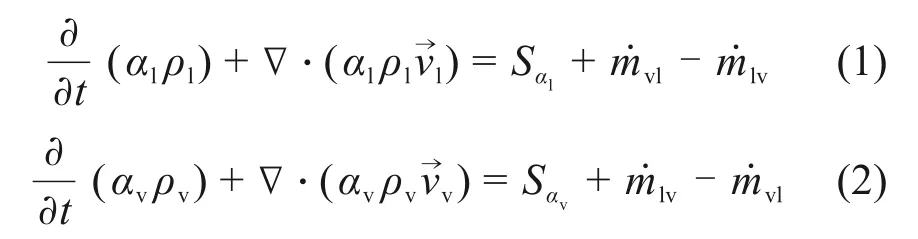
式中：αl和αv分别为液相和气相的体积分数；ρl和ρv分别为液相和气相的密度；和分别为液相和气相的速度；Sαl和Sαv分别为液相和气相的质量分数源相；和分 别为液相和气相间的 质 量传递。

动量方程：

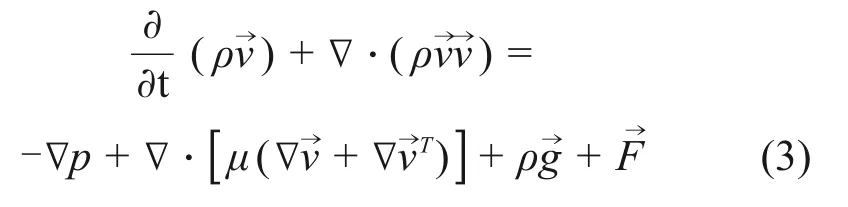
式中：ρ和分别为两相混合的密度和速度；为体积力；μ为黏性系数。

能量方程：

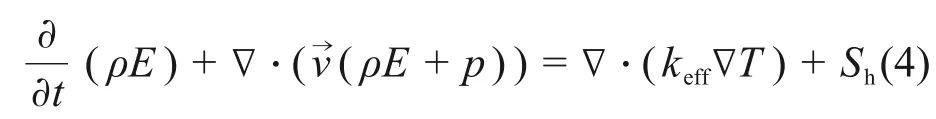
式中：keff为有效热导率；Sh为能量源相。

1.3 边界条件及算法设置

本文采用的工质为R134a，工作压力为5.7×105Pa，对应的饱和温度为20 ℃，并采用R134a 的物性参数为定值，如表1所示。本文中R134a的物性参数查阅自美国国家标准技术研究所(NIST)研发的工质物性参数计算软件REFPROP。

湍流模型采用k−ε模型，入口边界条件为速度入口，工质进口温度为饱和温度(20 ℃)，出口边界条件为压力出口(5.7×105Pa)。两相流模型采用VOF模型，用PISO算法求解压力−速度耦合方程。为节约计算时间并同时保证计算精度，采用变时间步长的计算方法，设置最大时间步长为1×10−5s，最小时间步长为1×10−8s，并控制库朗数为0.5。

2 仿真结果分析

2.1 流型

为了研究微通道内两相流型以及热点对流型的影响，首先研究了整体均匀热流密度下，热流密度和流速对流型的影响。图4所示为入口流速为0.1～0.5 m/s，整体均匀热流密度为20～200 W/cm2的工况下，微通道内70～90 mm处最终稳定时的两相流型。由图4可见：研究过程中出现了泡状流、受限泡状流、弹状流、拉伸气泡流以及环状流。

图4 热流密度和流速对流型的影响Fig.4 Influence of heat flux and velocity on flow pattern

由图4(a)～(c)可见：入口流速保持0.5 m/s 不变，当热流密度为20 W/cm2时，通道壁面因不断受热而达到一定过热度，在壁面的汽化核心处首先开始产生气泡，相邻的小气泡不断合并导致气泡体积不断增大，当气泡的尺寸达到脱离直径后，脱离壁面的气泡进一步生长并与下游气泡合并，从而形成泡状流。当进一步增大热流密度到100 W/cm2时，由于受通道高度的限制，气泡受热后其并不能在高度方向上进一步生长，只能沿通道长度方向发展成为受限气泡。当热流密度最终增大到200 W/cm2时，气泡的继续长大并进一步合并导致受限泡状流演变为弹状流。

图4(c)～(d)可见：热流密度保持200 W/cm2不变，当入口流速不断降低时，底面热源处的热量不能及时由冷却工质带出，导致气泡进一步膨胀。当流速降低至0.3 m/s 时，弹状流继续扩张导致液相区逐渐减小形成拉伸气泡流，并最终在流速降低至0.1 m/s时形成环状流。

基于上述结果，研究热点对两相流型影响。图5所示为入口流速为0.5 m/s，背景热流密度为20 W/cm2时，底面均匀热流密度为20 W/cm2与热点热流密度为500 W/cm2的流型对比图。由图5可知：局部热点的高热流密度对微通道内流型发展的影响并不大，当局部热点热流密度提高到500 W/cm2时，虽然气泡直径有所增大，但整体流型仍然呈现为泡状流。造成这种现象的原因是虽然局部热点的壁面温度有了大幅度提高，但是由于热点面积较小，主流流体流过热点区域时受热时间较短，后半段流体温升有限，导致高热流密度热点下微通道内整体流型变化不大。

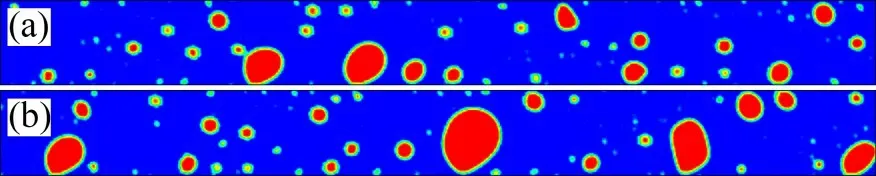
图5 不同热点热流密度下的流型Fig.5 Flow patterns under different heat flux of hot spot

2.2 温度

芯片温度对于其保持正常运行十分重要，而热点会对微通道内的温度分布带来极大负面影响。本文研究了热点对微通道不同区域的平均温度以及温度稳定性的影响。

图6所示为v为0.5 m/s，背景热流密度为20 W/cm2时，微通道底面不同区域壁面平均温度随热点热流密度的变化。由图6可知：随着热点热流密度提高，中间热点处的壁面温度不断上升，呈线性增长趋势；另外，热点对于微通道前半段的壁温几乎没有影响，而后半段因流体流过热点区域后一定程度上的受热，从而影响到了后半段的壁面冷却效果，导致后半段的壁温也有所提高。因此，微通道相变散热技术在解决局部高热流密度热点时有一定局限性，若要使热点处的壁面温度降到合适的芯片工作温度，则需要更高的泵功提供高质量流速，但此时除热点外的其他区域冷却效果溢出。在针对微通道热点处的冷却上，可结合一些其他散热方式，例如热电冷却技术，可在很大程度上抑制局部热点处的温升。

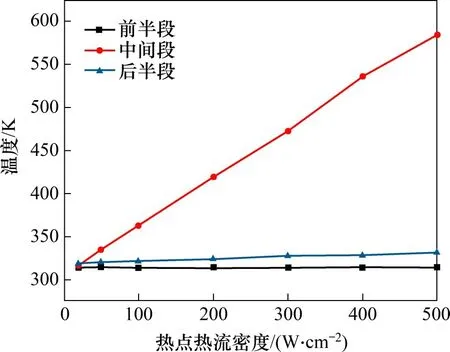
图6 热点热流密度变化下的底面不同区域平均温度Fig.6 Average temperature of different area of bottom under change of heat flux at hot spot

热点带来的问题不仅仅是局部高温，对于两相流动换热而言，热点也扩大了壁面温度的不稳定性。图7所示为v为0.5 m/s，背景热流密度为20 W/cm2时，微通道底面中间区域的壁面平均温度对比。由图7可知：当热点热流密度为20 W/cm2时，中间区域温度波动处于315～325 K；而当热点热流密度增加到500 W/cm2时，热点区域的温度波动提高至550～800 K。因此，对于微通道两相流动，当热点处热流密度提高至500 W/cm2时，在气泡未脱离热点时，附着于壁面的薄层液膜极易因高热流密度的作用下而被蒸干，导致热点处温度大幅上升，而当流动过程中后续工质对蒸干处液体进行补充或者当气泡脱离壁面时，热点处的温度则又会迅速下降。由此可见，高热点热流密度会引起热点区域的温度波动大幅提高，严重威胁到系统的安全稳定运行。

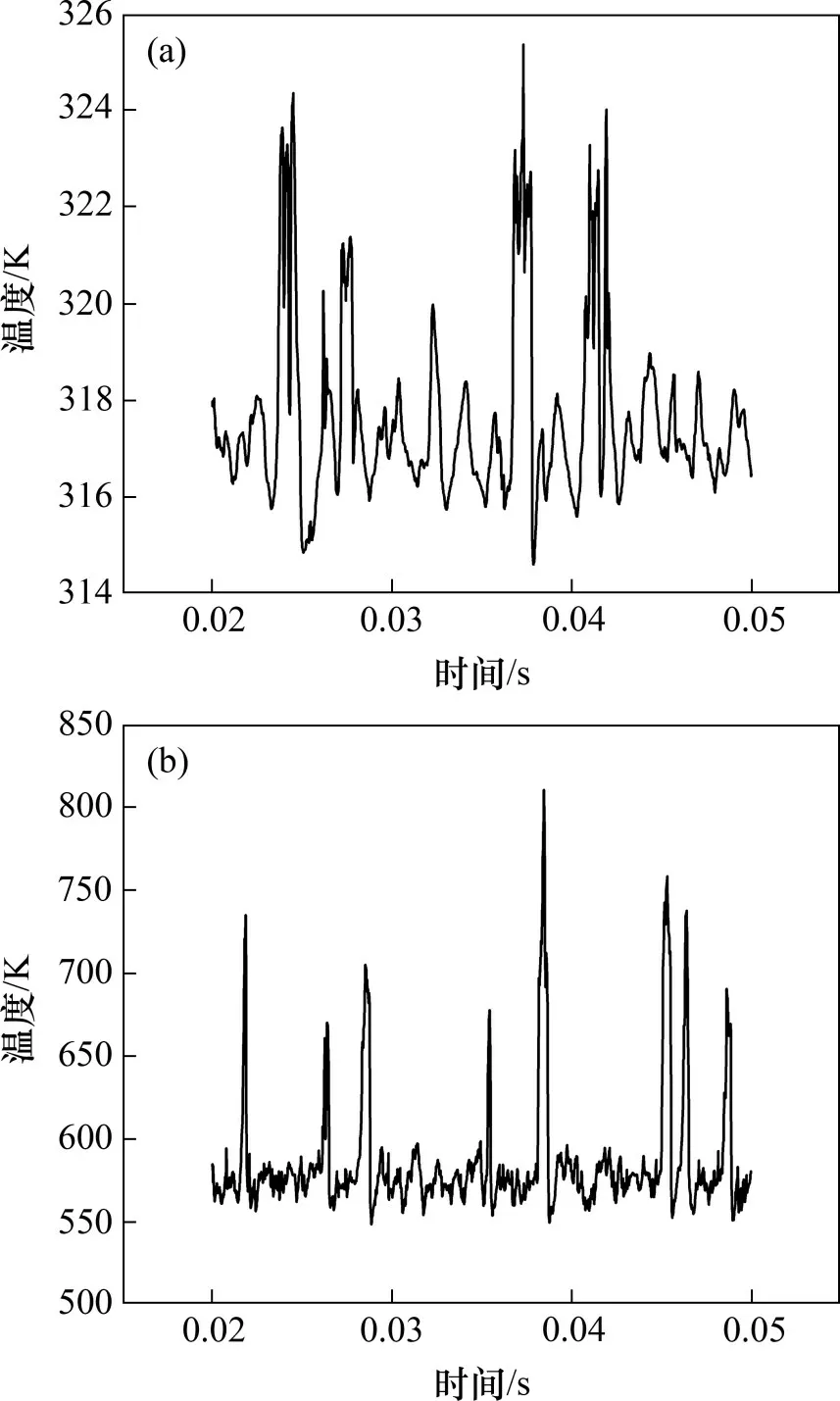
图7 不同热点热流密度下热点平均温度Fig.7 Average temperature of hot spot under different heat flux

2.3 换热系数

微通道内的流动换热是核态沸腾换热和对流沸腾换热综合影响的结果。为研究热流密度和流速对换热系数的影响，定义平均换热系数h：

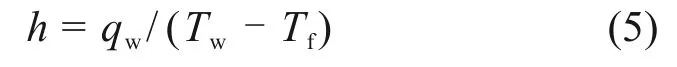
式中：qw为壁面热流密度；Tw为壁面平均温度；Tf为流体平均温度。

图8所示为不同流速下，底面换热系数随整体热流密度的变化。由图8可知：换热系数随着流速提高而增大。在流速一定的情况下，随着热流密度增大，换热系数呈现出先增大后减小的趋势。这主要是由于在流动沸腾的初始阶段，热流密度增大会使得汽化核心数量增加从而一定程度上提高了换热能力，但随着热流密度继续增大则会出现局部液膜的蒸干现象从而导致了换热系数开始不断下降。

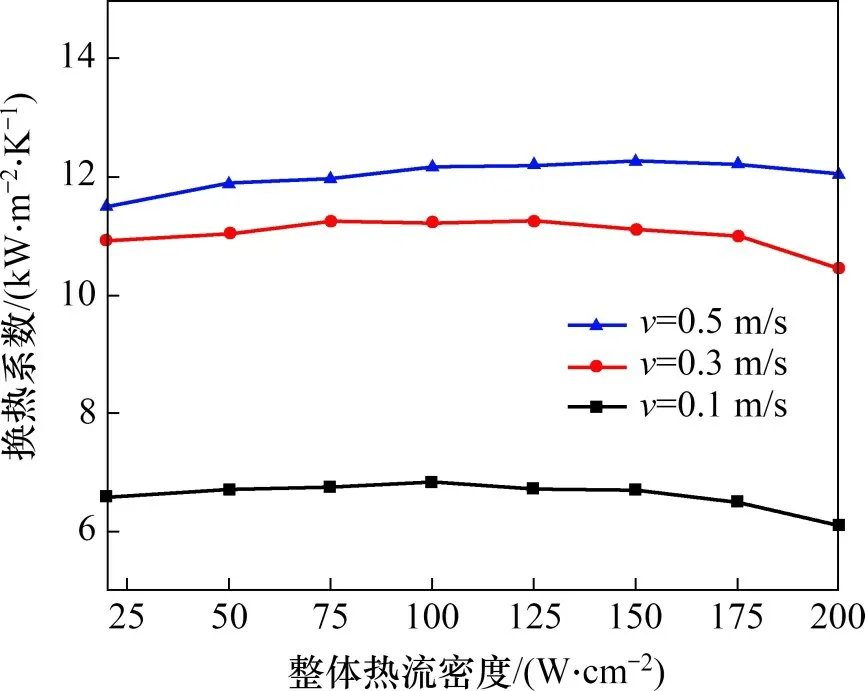
图8 整体热流密度变化下的底面平均换热系数Fig.8 Average heat transfer coefficient of bottom under the change of overall heat flux

目前研究中，少有文献探讨热点对不同区域换热系数的影响。本研究发现，引入热点对微通道不同区域的换热系数产生了不同的影响。图9所示为v为0.5 m/s，背景热流密度为20 W/cm2时，不同热点热流密度下，微通道不同区域的换热系数变化。由图9可知：微通道前半段的换热系数保持稳定，并不随热点热流密度增大而变化；中间段的换热系数随热点热流密度提高而上升，最终保持相对稳定，这是因为热点热流密度提高在一定程度上加快了该处气泡脱离壁面的过程，从而导致一定范围内换热效果有所增强，随后则保持稳定；而后半程的换热系数则随着热点热流密度上升而呈现出下降趋势，这是因为热点处热流密度提高导致后半程壁温迅速上升，而流体平均温升并不明显，其未充分带走壁面处的热量，因此引起换热温差增大从而导致换热系数降低。

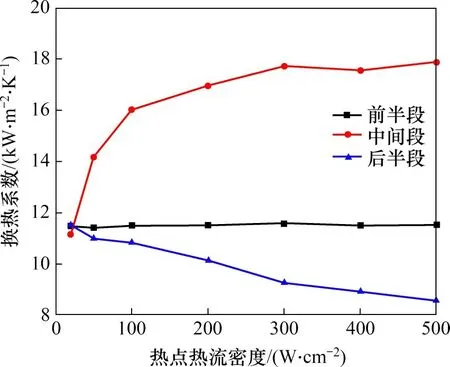
图9 热点热流密度变化下的底面不同区域平均换热系数Fig.9 Average heat transfer coefficient of different areas under the change of heat flux at hot spot

2.4 压降

微通道换热器虽然显著提高换热性能，但其也存在流动不稳定和流阻大等问题[21−22]，因此，压降也是研究微通道内流动换热的重点。

微通道内两相进口和出口压降取决于整体热流密度以及流速。图10所示为不同流速下，微通道进口和出口平均压降随整体热流密度的变化关系。由图10可知：两相压降随着流速增加而增大。流速增大意味着通道壁面以及气液两相之间的相对运动更加剧烈，从而引起了更大压降。另外，热流密度增大也会导致压降增大。这主要是由于随着热流密度增大，更多的液相工质向气相转变，气液两相混合物平均密度减小，一方面导致气液两相工质流速增加，另一方面热流密度增大也加剧了气泡生长，增加了气塞与通道壁面的摩擦。而对于热点而言，因研究的热点面积较小，在整体热流密度一定的情况下，提高热点热流密度并不会大幅改变进口和出口压降。

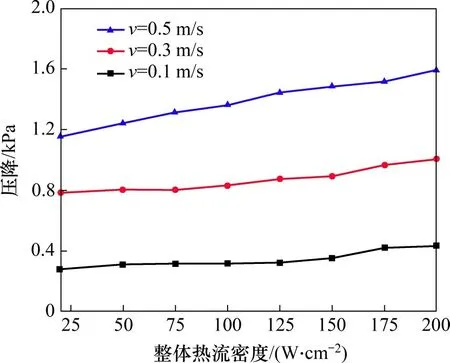
图10 整体热流密度变化下的进出口压降Fig.10 Pressure drop under different overall heat flux

不同于单相流动下的压降是相对稳定的，在两相流动过程中，随着时间推进，气泡的不断扰动会导致整个系统产生较大的压力波动。图11所示为v为0.5 m/s，背景热流密度为20 W/cm2时，热点热流密度为20 W/cm2与500 W/cm2时进出口压降对比。

由图11可见：在热点热流密度20 W/cm2与500 W/cm2时均出现了较大的压降波动现象，不利于系统的安全稳定运行。热点的高热流密度造成的压降波动差异并没有温度波动差异明显，热点热流密度为20 W/cm2和500 W/cm2的情况下，进口和出口压降的大致变化范围均在800～1 500 Pa。其主要原因在于局部热点热流密度提高对微通道内的整体气泡流型没有太大的影响。

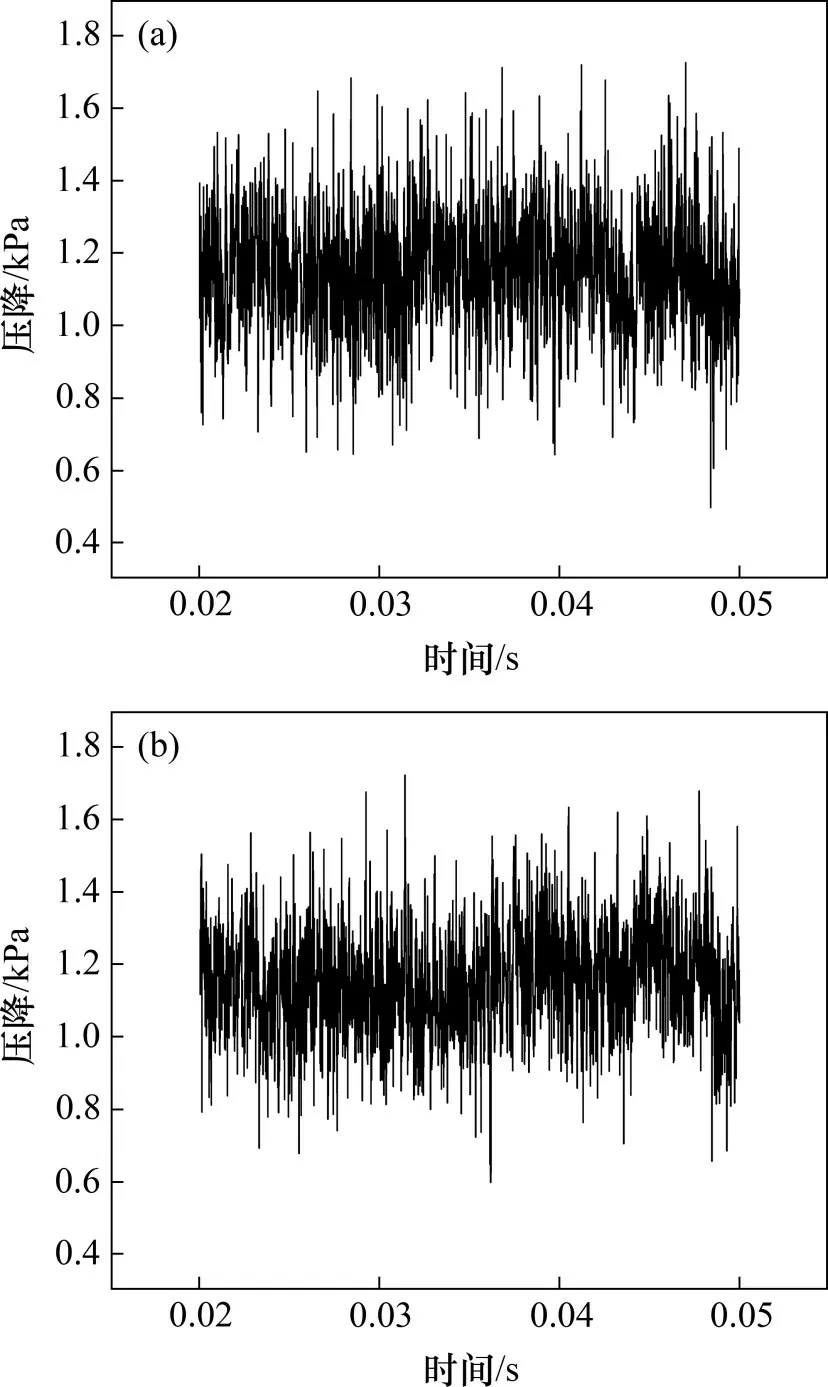
图11 不同热点热流密度下的进出口压降Fig.11 Pressure drop under different heat flux of hot spot

3 结论

1)在入口流速为0.1～0.5 m/s，整体均匀热流密度为20～200 W/cm2的工况下，微通道内的主要流型包括泡状流、受限泡状流、弹状流、拉伸气泡流以及环状流。在背景热流密度一定的情况下，热点热流密度提高只会一定程度上增大气泡直径，然而对微通道内的整体流型并不会产生较大影响。

2)热点处的高热流密度不仅会导致该处区域的平均温度迅速上升，而且会导致温度波动大幅度提高。通道前半段温度几乎不受热点影响，后半段则会因流体受热点的进一步加热从而导致壁温略有上升。

3)整体均匀热流密度条件下，换热系数受流速和热流密度两者综合影响。换热系数随着流速提高而增大，并且随着整体热流密度增大，换热系数呈现出先增大后减小的趋势。引入热点后，热点热流密度提高会一定程度上提高该处换热系数并造成通道后半段的换热系数有所降低。

4)随着流速和整体热流密度提高，进口和出口压降均会随之增大；而仅当热点处热流密度提高时，其对微通道内压降不稳定性的影响不大。