激活函数的发展综述及其性质分析

张 焕，张 庆，于纪言

（南京理工大学机械工程学院，智能弹药技术国防重点学科实验室，江苏 南京 210094）

近年来，深度学习[1]（deep learning,DL）成为人工智能（artificial intelligence，AI）相关领域中发展最快、最有活力的研究方向之一。卷积神经网络（convolutional neural networks，CNN）作为深度学习的最重要组成部分，其应用范围越来越广，在语音识别、自然语言处理、图像识别等领域表现优异[2−6]。卷积神经网络是由传统的人工神经网络[7−9]（artificial neural network,ANN）发展而来。激活函数（activation functions）是卷积神经网络的一个必不可少的部分，它增加了网络的非线性表达能力。

激活函数可以看作卷积神经网络模型中一个特殊的层，即非线性映射层。卷积神经网络在进行完线性变换后，都会在后边叠加一个非线性的激活函数，在非线性激活函数的作用下数据分布进行再映射，以增加卷积神经网络的非线性表达能力。从模仿人类神经科学的角度来看，激活函数在模型中对数据的作用过程是模拟了生物神经元对电信号的处理过程。生物神经元的作用过程是设定一定的阈值激活或抑制接收到的电信号而进行生物信息和信号的传播。模拟生物神经元的作用过程，理想的激活函数应该是将输入数据通过一定的阈值直接输出为“0”“1”这2 种结果。但是，卷积神经网络模型在前向传播、误差反向传播的过程中要求激活函数具备连续性、可微性等性质，显然目前理想生物神经元激活函数不符合该要求。激活函数的自身函数性质决定了在作用过程的优势和缺陷。研究激活函数的性质，分析激活函数性质与优缺点的关联性，寻找时间、空间及特征采集度高效的激活函数成了一项比较重要的研究内容。

1 卷积神经网络中常见的激活函数

在深度学习发展初期，传统S 型非线性饱和激活函数sigmoid 和 tanh 函数得到了广泛的应用[10]。然而，随着模型深度的提高，S 型激活函数出现了梯度弥散的问题，这也是早期神经网络不能深度化发展的原因之一[11−15]。2010 年，Hinton 首次提出了修正线性单元[16]（rectified linear units，ReLU）作为激活函数。Krizhevsky 等[1]在2012 年 ImageNet ILSVRC 比赛中使用了激活函数ReLU。ReLU 表达式简单易于求导，使得模型训练速度大大加快，且其正半轴导数恒定为1，很好地解决了S 型激活函数存在的梯度弥散问题。但是ReLU 激活函数在负半轴的梯度始终为0，在模型学习率设置较大情况下，会发生神经元“坏死”的情况[17−18]。

为了解决ReLU 激活函数的负半轴“神经元坏死”的情况，研究者们提出Leaky ReLU[19]、PReLU[20]、Noisy ReLU[21]、ELUs[17]、ReLU-softplus[22]、ReLUsoftsign[23]、TReLU[24]等激活函数。这些激活函数有效缓减了“神经元坏死”的问题。下面将详细介绍各类激活函数的性质、优缺点，并总结得到优秀激活函数应该具备的特性。

1.1 sigmoid 和tanh 激活函数

sigmoid 和tanh 激活函数是深度学习初期常用的S 型激活函数，其函数、导数数学表达式为式（1）（2）（3）（4）；其函数、导数图像如图1、图2 所示。

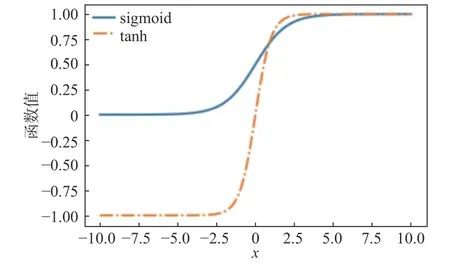
图1 sigmoid 和tanh 的函数图

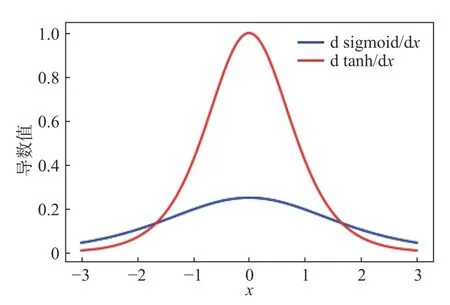
图2 sigmoid 和tanh 的导数图

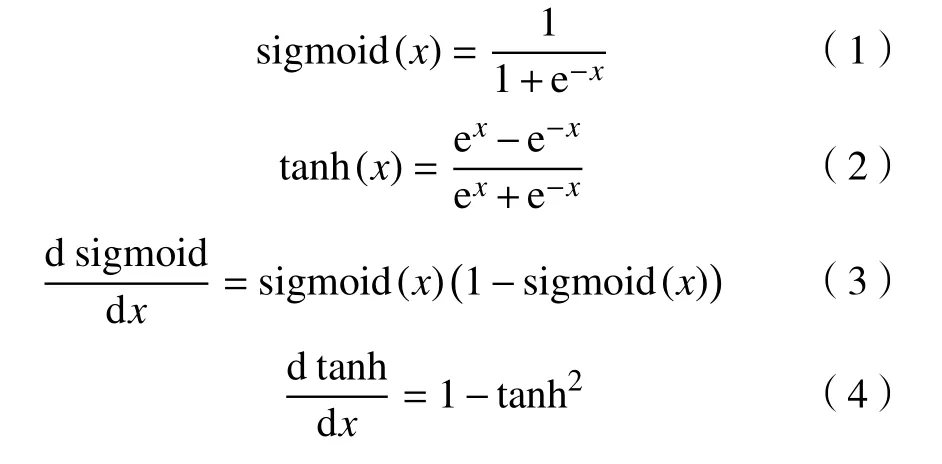
由图1 知：sigmoid 激活函数值的范围为（0，1），经过它激活得到的数据为非0 均值；sigmoid 激活函数具有双向饱和性，即在一定数据范围内，其导数趋于0 收敛。由图2 可知：sigmoid 激活函数导数范围为（0，0.25），且不在（−3，3）的数据导数值很小，在反向传播过程时，导数相乘很容易造成梯度弥散；sigmoid 激活函数求导过程计算量较大，模型训练的时间复杂度较高。由图1、图2 对比知：tanh 激活函数解决了sigmoid 激活函数非0 均值的问题，且其导数范围为（0，1），从而略微缓减了sigmoid 激活函数梯度弥散的问题；但tanh 激活函数存在的双向饱和性仍然使得梯度弥散问题存在，且模型训练的时间复杂度较高。

1.2 ReLU、Nosiy ReLU、Leaky ReLU、PReLU、RReLU 激活函数

激活函数ReLU 的提出和应用很好地解决了sigmoid 和tanh 函数存在的“梯度消失”问题。ReLU 可以扩展为包括高斯噪声的Noisy ReLU（noisy rectified linear unit），其在受限玻尔兹曼机解决计算机视觉任务中得到应用[21]。

虽然ReLU 函数的稀疏性很好地解决了“S 型”软饱和激活函数带来的梯度消失的问题，但是ReLU 负半轴存在的硬饱和置0，这可能会导致“神经元坏死”，也使得它的数据分布不为0 均值，模型在训练过程可能会发生神经元“坏死”的状况。为了解决Relu 负半轴“神经元坏死”的情况，研究者们对ReLU 的负半轴下功夫改造，提出了Leaky ReLU（leaky rectified linear unit）、PReLU（parametric rectified linear unit）、RReLU（randomized leaky rectified linear unit）等激活函数。其中，RReLU最初是在Kaggle NDSB 竞赛中得到使用。以上所提到的函数数学表达式为式（5）（6）（7）（8）（9），表达式中a为小于1 的正数，它们的函数图像如图3所示。

图3 几种“变种”ReLU 激活函数的函数图

由式（5）（7）（8）（9）以及图3 知，Leaky ReLU、RReLU 和PReLU 分别通过手动、随机以及待训练的方式在负半轴添加一个很小的线性参数，其目的是在一定程度上缓减ReLU 负半轴硬饱和的问题，但是引入的参数给模型训练带来了一定的麻烦。由式（6）知，Noisy ReLU（noisy rectified linear unit）在正半轴添加了高斯噪声，但是和ReLU 存在一样的问题。

1.3 ReLU6 与神经元的稀疏性

ReLU 的稀疏性给卷积神经网络的训练带来了巨大的成功。无独有偶，2003 年Lennie 等估测大脑同时被激活的神经元只有1%～4%，进一步表明神经元工作的稀疏性。神经元只对输入信号的少部分选择性响应，大量信号被刻意的屏蔽。类似神经元信号传播，在一定模型下，ReLU 的稀疏性可以提高学习的精度。然而传统的sigmoid 激活函数几乎同时有一半的神经元被激活，这和神经科学的研究不太相符，可能会给深度网络训练带来潜在的问题。

在深度学习中，有研究者尝试使用ReLU6 激活函数。ReLU6 是在ReLU 激活函数的基础上将大于6 的数据部分置为0，以进一步提高连接的稀疏性。式（10）为ReLU6 的函数表达式，图4、图5 为其函数、导数的图像，图6 为稀疏性连接的示意图。

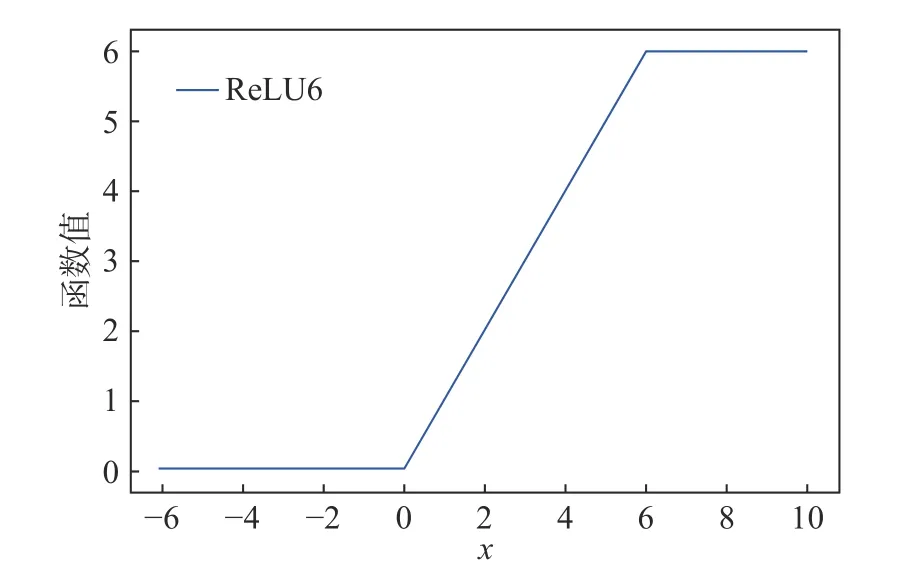
图4 ReLU6 函数图

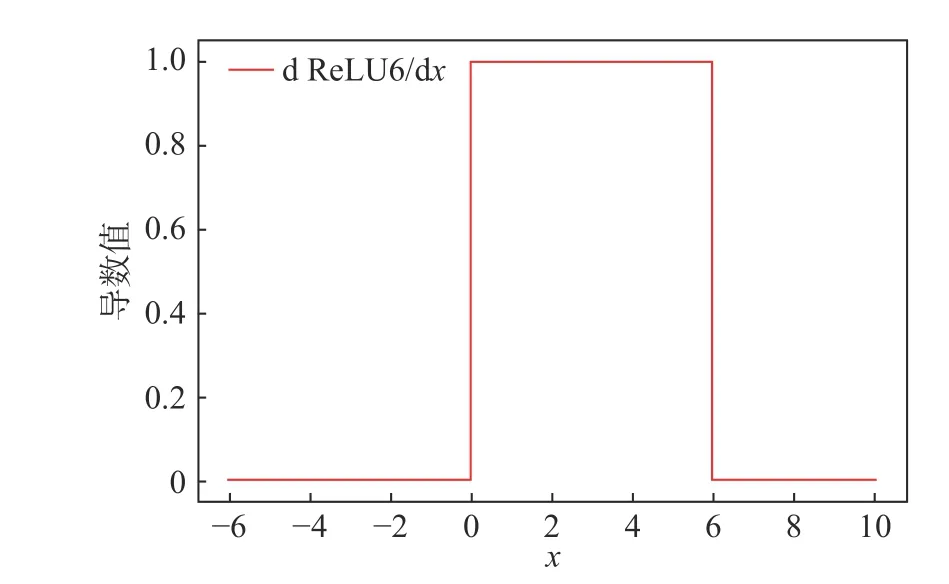
图5 ReLU6 导数图

图6 稀疏性连接示意图

1.4 Swish 和Xwish 激活函数

Swish 激活函数[25]是谷歌提出的一个效果更优于ReLU 的激活函数。经过测试，在保持模型其他参数不改变的条件下，只把原模型中的ReLU激活函数修改为Swish 激活函数，模型的准确率均有提升。Swish 激活函数的数学表达式为式（11）所示，函数图像为图7 所示，导数图像为图8 所示。式（11）中β是常数或可训练的参数。Swish 激活函数没有上界有下界，具有可微、非单调的性质。当β=0 时，Swish 变为线性函数；当β→ ∞,Swish 成为了ReLU 函数：因此，可以将Swish 函数看成线性函数和ReLU 函数之间的线性插值的平滑激活函数。

图7 Swish 函数图

图8 Swish 导数图

刘宇晴等提出的Xwish 激活函数[26]与Swish激活函数有相似的函数曲线及性质。其函数、导数数学表达式为式（12）（13）所示，函数、导数图像为图9、图10 所示。

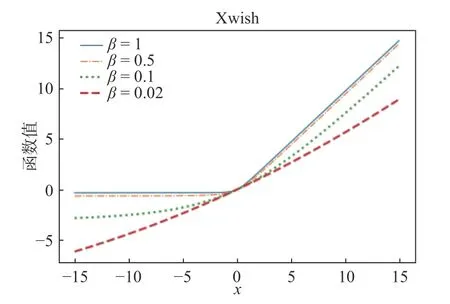
图9 Xwish 函数图

图10 Xwish 在不同参数下的导数图

1.5 Maxout 激活函数

Maxout 激活函数的原理是通过线性分段函数来拟合可能的目标凸函数，并将其作为激活函数。它可以看作在卷积神经网络中添加的一层激活层。它包含1 个参数k。相比其他激活函数，它的特殊之处在于，增加了k个神经元，经过神经元输出最大的激活值。Maxout 激活函数可以看作ReLU激活函数的推广。Maxout 激活函数能增强Dropout函数的功能，实验证明二者一起使用时能发挥比较好的效果[27]。

任意的凸函数都可以由分段线性函数拟合，而Maxout 取k个线性隐藏层节点的最大值。图11依次示出Maxout 激活函数拟合线性激活函数、绝对值激活函数、二次激活函数的过程。图中展示了在一维输入下Maxout 激活函数拟合二维平面函数的过程。实际上，Maxout 激活函数可以逼近拟合更高维度的凸函数。Maxout 具有ReLU 的优点，即线性和不饱和性，同时它也解决了ReLU 存在的“神经元坏死”的问题。但是，Maxout 引入了训练参数而导致了模型整体参数数量的激增，导致模型的复杂度增高。

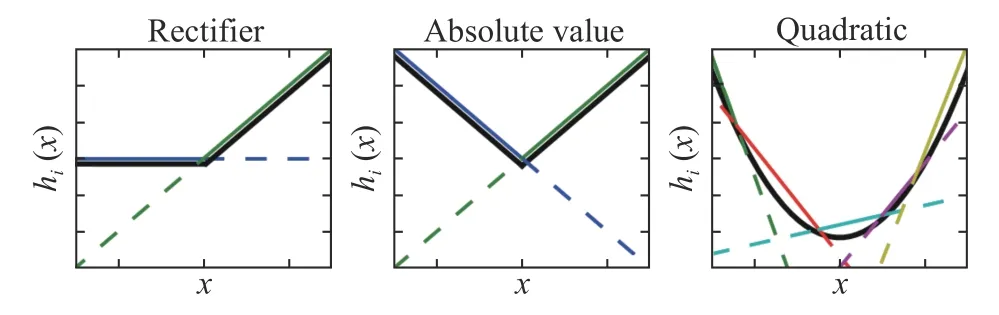
图11 Maxout 示意图

1.6 ELU 和TReLU 激活函数

ELU 和TReLU 激活函数的正半轴与ReLU 激活函数保持一致，通过对负半轴引入软饱和以代替置“0”。式（14）（15）为ELU 激活函数的函数、导数数学表达式，图12、13 为其函数、导数图像。从数学表达式（14）（15）和图12、13 可以看出，ELU 激活函数[13]在正半轴具有与ReLU 激活函数一样的优势，同时引入了负半轴的定义使得整体输出均值接近0。与LeakyReLU 和PReLU 相比，虽同样都是激活了负半轴，但ELU 的负半轴为软饱和区，斜率具有衰减性，这使得其对噪声有一些鲁棒性。同时，参数a控 制着函数的斜率变化。

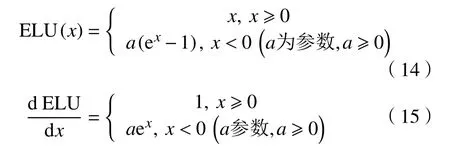
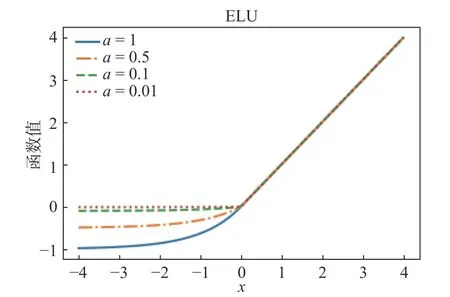
图12 ELU 在不同参数下的函数图

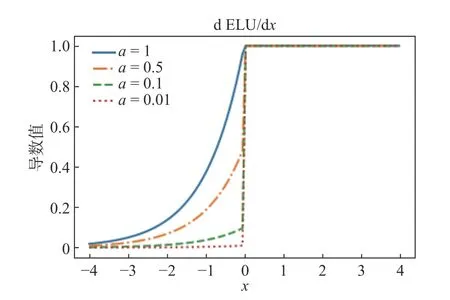
图13 ELU 在不同参数下的导数图

张涛等同样提出了负半轴为饱和区的TReLU激活函数[24]。式（16）（17）为其函数、导数数学表达式。式中a为可变参数，用来控制非饱和区域的斜率变化。TReLU 拥有和ELU 相似的优势：缓减了梯度弥散的问题；激活了负半轴，从而缓减了“神经元坏死”的问题；近似于0 均值分布；负半轴的软饱和性使得其对噪声具有鲁棒性。图14、15 为其函数、导数图像。

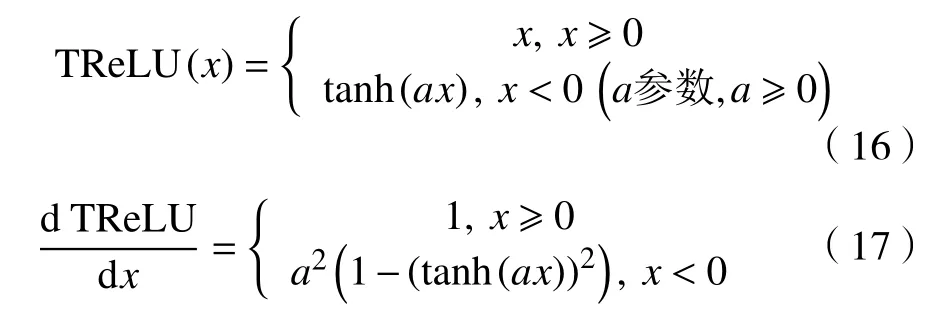
图14 TReLU 在不同参数下的函数图

图15 TReLU 在不同参数下的导数图

1.7 softplus、softsign 和relu-softplus、relu-softsign激活函数

softplus 是对所有输入数据进行非线性映射的一种激活函数。式（18）（19）为其函数、导数表达式，图16、图17 为其函数、导数图像。从数学表达式和函数图像可以看出：softplus 无上界，具有负半轴单向软饱和性，函数值始终大于0；同时引入了对数和指数运算，计算量较大。

图16 softplus 和softsign 函数图

图17 softplus 和softsign 导数图

softsign 激活函数是一种双向软饱和“S 型”激活函数，可以看作tanh 激活函数的改进版。式（20）（21）为其函数、导数表达式，图16、图17 为其函数、导数图像。图18 示出softplus、softsign、tanh 的函数图像比较结果。图19 示出softplus、softsign、tanh 的导数图像比较结果。从式（20）（21）和图18、图19 可以看出，softsign 激活函数是0 均值分布的，且相比于tanh 激活函数，softsign 激活函数的曲线变化更加平缓，其导数下降的速率较慢。从理论上看，相较于tanh 激活函数，其能够进一步缓减双向软饱和“S 型”激活函数存在的梯度弥散问题。

图18 softplus/softsign/tanh 函数对比图

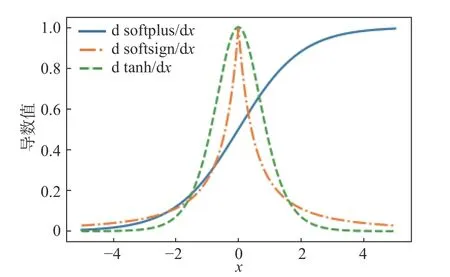
图19 softplus/softsign/tanh 导数对比图

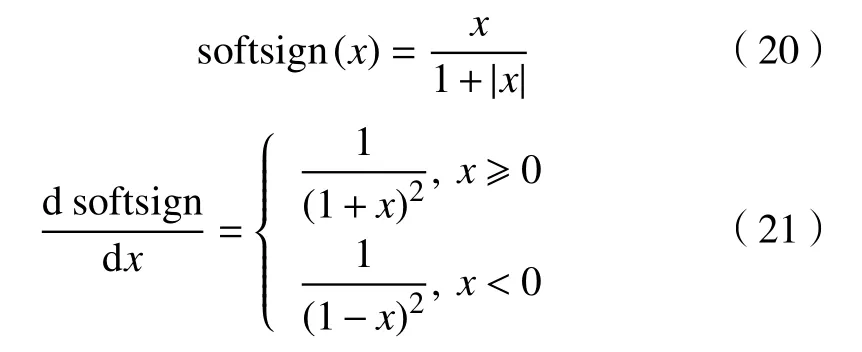
曲之琳等[22]将ReLU 激活函数和softplus 激活函数进行了结合，并对softplus 的负半轴做减常数ln2 处理，提出了relu-softplus 组合激活函数。式（22）（23）为其函数、导数表达式，图20、图21 为函数、导数图像。和ELU、TReLU 等激活函数一样，relu-softplus 激活函数的负半轴软饱和缓减了“神经元坏死“问题，且负半轴做减常数处理，巧妙地完成了与正半轴的连接。但是relu-softplus 激活函数存在指数，在负半轴零点附近的导数存在突变，持续减小直至0。其存在的问题是对学习率要求较高：若学习率设置过大，容易出现模型不收敛的问题；学习率设计较小，模型收敛得慢。

王红霞等[23]将ReLU 激活函数和softsign 激活函数进行了结合，提出了relu-softsign 组合激活函数。式（24）（25）为其函数、导数表达式，图20、图21 示出relu-softplus 和relu-softsign 的函数、导数的比较结果。从公式（24）（25）以及图20、图21 中可以看出：relu-softsign 激活函数在正半轴为线性单元，其导数始终为1，这一特点保证了模型的加速收敛；relu-softsign 激活函数在负半轴为softsign 激活函数的负半轴软饱和部分，其导数在零点不存在突变，导数值由1 减小至趋于0。relusoftsign 激活函数由于在负半轴提供的非0 导数，增加了对非正值处理的鲁棒性，也加速了模型的收敛速度。

图20 relu-softsign 和relu-softplus 函数图

图21 relu-softsign 和relu-softplus 导数图

比较二者的负半轴斜率，由图20、图21 可以看出，relu-softsign 激活函数在负半轴零点附近较relu-softplus 激活函数整体有更大的导数，前者在零点附近导数由1 衰减较快，但保证了模型在零点附近的数据特征下有较快的收敛性；后者在零点附近导数值由1 突变为0.5，相较于前者，其模型在零点附近的数据特征下收敛性不足。王红霞等[23]通过仿真实验验证了此理论分析。

2 激活函数的性质分析

依据上文的讨论及激活函数的发展规律，可以初步得出一个良好的激活函数常具备以下一些特点：1）非线性以及可微性；2）解决梯度消失问题，也避免出现梯度爆炸问题；3）解决“神经元坏死“问题；4）符合或近似符合0 均值分布；5）计算的时间、空间复杂度小；6）存在一定的稀疏性；7）模型收敛速度相对较快；8）对数据噪声具有一定的鲁棒性等。

sigmoid 和tanh 激活函数符合1）、4）特点，但不符合2）、5）、6）、7）；ReLU 激活函数缓和了“S”型激活函数存在的问题2）、5）、6）、7），但是引入了问题3）、4）；Nosiy ReLU、Leaky ReLU、PReLU、RReLU 激活函数对ReLU 激活函数负半轴进行改造，缓减了ReLU 激活函数存在的问题3）；ReLU6激活函数引进稀疏性，因此符合特点6）、8）；Swish和Xwish 激活函数可看成线性函数和ReLU 函数之间的线性插值的平滑激活函数，其保留了负半轴的特征，缓和了ReLU 存在的问题3）、4）；Maxout激活函数缓和了ReLU 激活函数存在的问题3），但是引入参数也带来了问题5）；ELU 和TReLU 激活函数缓减了ReLU 激活函数的问题3）、4），且引入的软饱和满足特点8）；relu-softplus、relu-softsign激活函数结合了softplus/softsign 和ReLU 的正负半轴，不但缓和了ReLU 激活函数存在的问题3）、4），且符合特点7）、8），将激活函数负半轴斜率变化快慢和模型收敛速度结合了起来。

为了进一步分析激活函数的性质，本文以多层感知机为例，推导激活函数在前向传播和反向传播过程中的作用表达式。

2.1 损失函数

在多层感知机中，给定样本集合，其整体代价函数为式（26）。其中，前一项为误差项，常见的有平方误差项、交叉熵误差项等；后一项为正则化项，此处使用的是L2 正则化。

2.2 前向传播

多层感知机中，输入信号通过各个网络层的隐节点产生输出的过程称为前向传播。在网络训练过程中，前向传播会生成一个标量损失函数。定义第i层的输入、输出为x[i]、a[i],上一层的输出作为下一层的输入。w[i]、b[i]为 第i层的权值参数和偏置，z[i]是 第i层 输入神经元未经激活的值，g[i](x)为 第i层的激活函数。前向传播过程的表达式为

分析式（27），在神经网络的前向传播的过程中，输入和本层的权值相乘，加上偏置，并将各项结果累加，得到下一层神经元的初步输入值，其与上一层的关系为线性关系。这个初步输入值经过激活函数的加工，对初步输入值进行非线性映射，增强了表达能力。因此激活函数应该具备以下性质：

1）激活函数具有较强的非线性表达能力；

2）激活函数应该符合或近似符合0 均值分布条件，以增加其对数据的适应性；

3）激活函数应该具有良好的计算特性。

2.3 反向传播

多层感知机中，反向传播过程是将损失函数的梯度信息沿着网络向后传播，以更新权值参数。其过程是将 da[j]作 为输入,得到 dw[j]、db[j]，作为输出，a为学习率，其余参数表达参照2.2 中的前向传播，其过程表达式如式（28）—（34）所示。

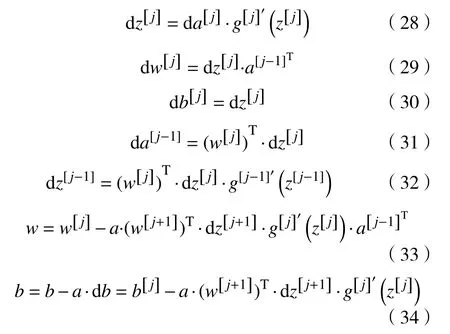
对于sigmoid 激活函数，其求导展开式为

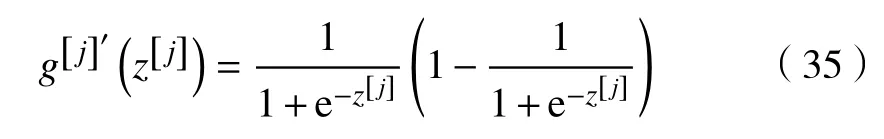
对于tanh 激活函数，其求导展开式为

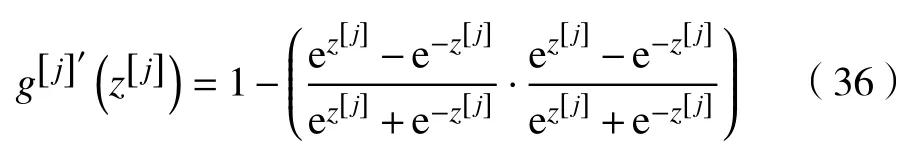
对于ReLU 激活函数，其求导展开式为

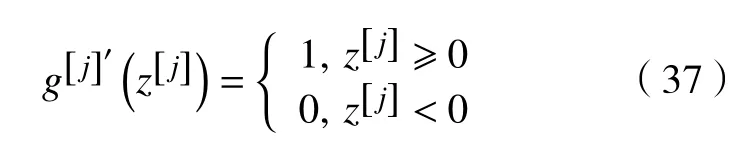
对于ReLU6 激活函数，其求导展开式为

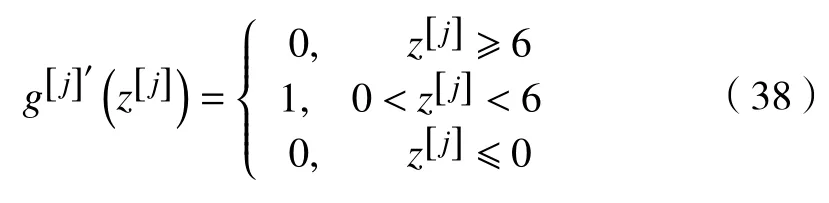
对于Xwish 激活函数，其求导展开式为

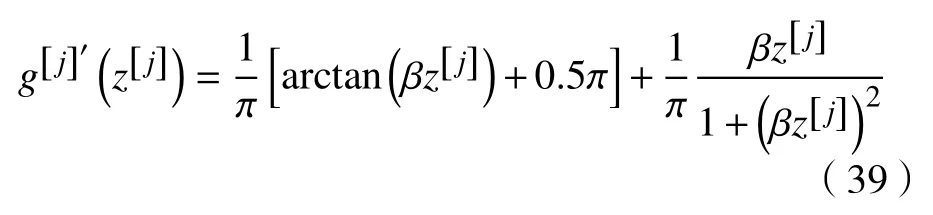
对于ELU 激活函数，其求导展开式为

对于TReLU 激活函数，其求导展开式为

对于relu-softplus 激活函数，其求导展开式为

对于relu-softsign 激活函数，其求导展开式为

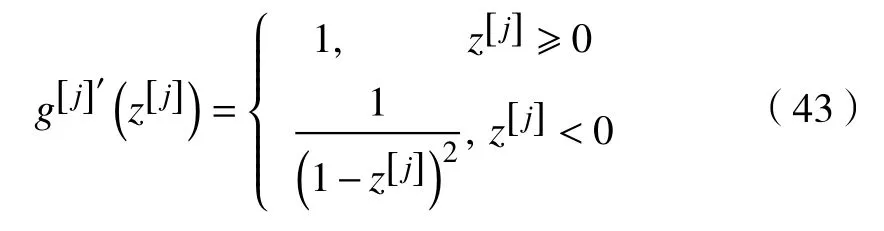
分析式（28）—（43），可以得出，权值参数(Wb)的更新与激活函数导数值的大小存在线性相关关系，深层神经网络的参数更新中会出现激活函数的导数连乘。因此分析反向传播过程，激活函数应该具备以下性质：

1）在连乘情况下避免出现梯度消失问题，也避免出现梯度爆炸问题；

2）避免出现激活函数导数过于置0 从而导致参数不更新，出现“神经元坏死“问题；

3）激活函数的导数计算的时间、空间复杂度应该较小；

4）由神经科学学科的研究论证，激活函数应该存在一定的稀疏性；

5）模型刚开始训练的时候，激活函数的导数应该较大，加速模型收敛，在模型收敛后半段，激活函数有一定的软饱和性，即导数渐渐趋于0，使得模型收敛至最优值；

6）参数w的更新方向与该层的输入a[j−1]有关，参数的更新方向应该自由，因此应该选择一个正负值都可以输出的激活函数；

7）模型对数据噪声应具有一定的鲁棒性，因此激活函数应该具备一定的饱和性。

3 结束语与展望

本文较详细地列举了激活函数的发展历程及当前主流激活函数所固有的特点，并推导了多层感知机的前向传播、反向传播过程，结合激活函数的发展经验提出了优良激活函数应该具备的一些性质。这为深入了解激活函数提供了便利，为研究改进激活函数提供了一种思路。随着计算机计算水平以及深度学习理论的不断发展，激活函数的角色还会发生变化。未来可能从以下几个方向突破：1）从计算机的计算能力限制中解放出来，应用更复杂、特征映射更精细的激活函数；2）深度学习理论的重大突破及神经科学的解密可能会带来激活函数发展的新思路；3）在ReLU 激活函数的模板下，对激活函数进行负半轴改造；4）稀疏性连接理念在激活函数中的应用启发；5）针对特定任务应用而设计激活函数（精度与时间复杂度的权衡）。

激活函数作为卷积神经网络的一个必不可少的组成部分，不论是在ReLU 的基础上进行改进，还是构造全新激活函数；不论是通用型激活函数，还是单适用性激活函数：其最终的目的是为了增强或更快速地对数据特征进行非线性映射，最终实现模型的高泛化能力或低时间复杂度。