低比转速离心泵驼峰稳定性及其影响因素研究
杨军虎,李淑萍,阎世杰,张欣娟,李 瑶,李怀瑞
(1.兰州理工大学能动学院,甘肃 兰州 730050;2.甘肃省流体机械及系统重点实验室,甘肃 兰州 730050)
低比转速离心泵在国民经济中应用广泛,但其效率较低。为了提高其效率,一般将离心泵叶轮叶片出口角取得较大,但这会使离心泵扬程-流量特性曲线产生驼峰,引起泵运行不稳定,甚至导致泵停机。
国内外学者对低比转速离心泵扬程-流量曲线的稳定性做了大量研究。文献[1]指出:离心泵叶轮叶片出口角越大,理论扬程曲线就越平坦,因此一旦在小流量区产生较大的水力损失,特性曲线就容易产生驼峰。文献[2—3]通过理论扬程与叶轮内损失的理论分析和数学推导,对特性曲线形状进行初步预测,得出特性曲线产生驼峰的判据,并提出减小出口角度、出口宽度、叶片数能够提升特性曲线的稳定性。文献[4]研究了进口有预旋的低比转速离心泵扬程–流量曲线稳定性的问题,通过推导发现进口正的预旋角能够使离心泵的理论扬程–流量曲线变陡,提升离心泵性能曲线的稳定性。文献[5]以一台低比转速离心泵为研究对象,采用叶轮出口边斜切,并且斜切比例(切割前的后盖板直径与切割后的后盖板直径之比)在0.9~1 之间,能够消除特性曲线的驼峰,其对效率的影响较小,但是扬程有一定下降。叶轮轴面倾斜、叶片进口边前移也能够提升特性曲线的稳定性,它们对扬程的影响较小,但是大流量区效率下降明显。文献[6—9]针对离心泵特性曲线产生驼峰的机理进行研究,发现扬程–流量曲线有驼峰现象的泵的叶轮出口处会出现较强的射流–尾迹现象,而扬程–流量曲线没有驼峰的泵的叶轮出口处相对速度变化较小,射流-尾迹现象基本消失。
从以上分析可知,对于一般的低比转速离心泵,能够提升扬程–流量曲线稳定性的因素有叶轮出口边斜切、叶轮轴面倾斜、叶片进口边前移等,但这些因素对离心泵扬程、效率会产生不利的影响。目前,对于这些因素能够提升扬程–流量曲线稳定性的机理尚不清楚,它们共同作用对扬程–流量曲线稳定性的影响还未见报道。本文基于数值模拟与试验相结合的方法,根据影响特性曲线稳定性的因素建立正交表,探讨各影响因素对特性曲线的作用机理,以期提高扬程–流量曲线的稳定性。
1 正交方案设计
1.1 研究对象
以一台国内某水泵厂生产的流量Q=12.5 m3/h、扬程H=31.25 m、转速n=2 900 r/min、比转速为47 的离心泵为研究对象。该泵在设计时,为了提高其效率,将出口角取得较大(β2=42°),泵的扬程–流量曲线驼峰明显。其叶轮设计参数见表1。
1.2 试验因素和试验方案
为了提高低比转速离心泵扬程–流量曲线的稳定性,根据泵的设计理论和文献[5]中得到的经验值,选择叶轮出口边斜切比、叶轮轴面倾斜、叶轮出口角、叶片包角、叶片的进口边平均半径5 个因素,每个因素选取4 个合理水平,获得如表2 所示的研究方案,选用L16(45)正交表,确定16 组试验方案,如表3 所式。
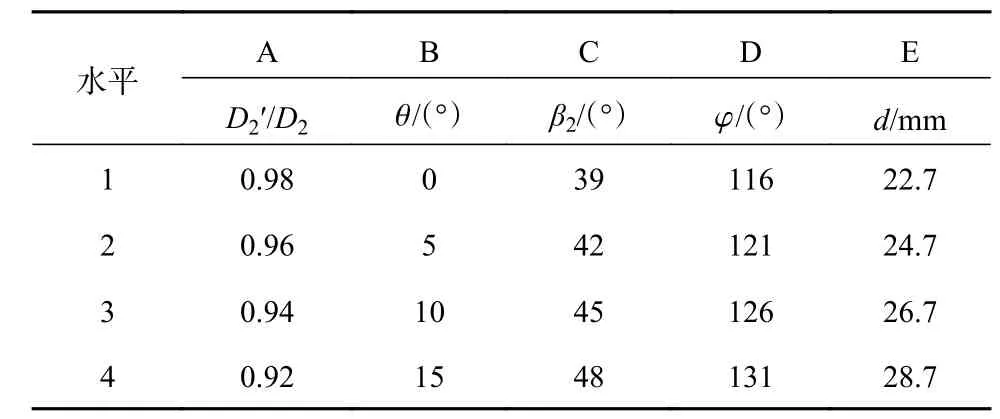
表2 各因素的研究方案
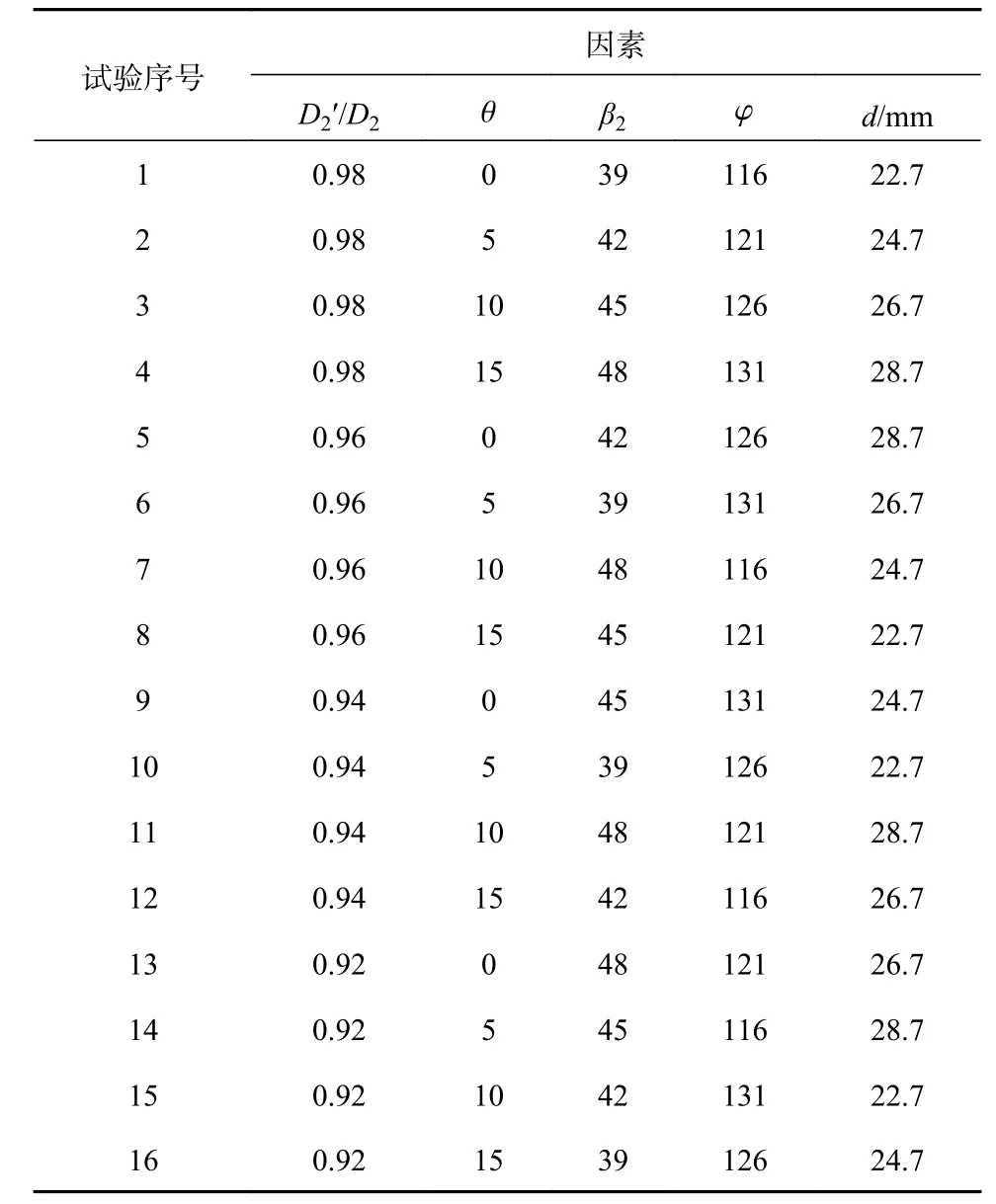
表3 正交试验方案
2 数值模拟与外特性试验验证
2.1 数值模拟
2.1.1 三维建模及网格划分
采用全流道模拟单级单吸式离心泵的流动特性,应用Creo3.0 软件进行三维造型,导入ICEM 17.0 内采用四面体非结构网格划分。原模型泵的全流场三维展开图如图1 所示。
图1 原模型的全流场三维展开图
2.1.2 边界条件及网格无关性检查
网格在ICEM 17.0 内生成后,导入Ansys-Fluent17.0 软件内进行定常数值模拟计算,采用RNGk-ε湍流模型,进口设置为速度进口,出口设置为自由出流。压力与速度的耦合方法为SIMPLEC算法,计算精度为10−5,迭代步数6000 步。
数值模拟前进行网格无关性检查,当网格数大于210 万时,计算求得的扬程和效率基本保持不变,则网格数量在210 万以上合适。其他的试验模型网格数量均与该数量相当。
2.2 数值模拟和试验结果的对比
2.2.1 外特性试验
为了验证模拟数据的准确性,在图2 所示的兰州理工大学离心泵试验台上对原型泵进行了外特性试验。

图2 离心泵试验台
试验中通过调节阀门来控制流量的变化,并用流量计来监测流量大小。压力传感器测量进出口压力,利用转矩转速仪测量泵的输入转矩、转速,即可以计算得到泵的输入、输出功率及效率。
2.2.2 外特性试验对比
采用全流道数值模拟与试验得到的数据如图3 所示。原模型泵的驼峰发生在流量为6.125 m2/s 处,即设计流量的0.5 倍。试验与数值模拟得到的扬程–流量、效率–流量、轴功率–流量在各个工况吻合较好,趋势一致。由此可知本文采用数值模拟的方法能够对泵运行的小流量区域内部流场进行比较准确的模拟,但是数值模拟扬程的结果略高于试验,模拟试验的效率略高于试验效率。这是由于数值模拟忽略了轴承和轴封等引起的摩擦损失。
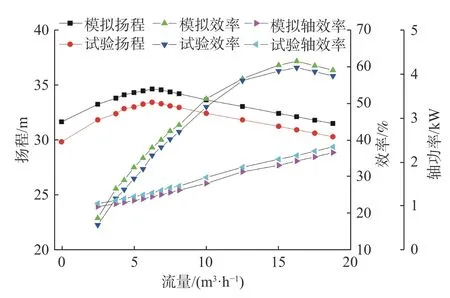
图3 模拟值与试验值对比
3 结果分析
3.1 离心泵扬程–流量曲线稳定性的判据
由图4 可知,离心泵的扬程–流量曲线稳定性与其在关死扬程点和水平轴所夹的角度 α(包含正负)有关。α的值越小,曲线越稳定,越不容易产生驼峰;α的值越大,曲线越不稳定,越容易产生驼峰。α的值为正,代表扬程–流量曲线有驼峰;α的值为负,代表扬程–流量曲线没有驼峰。因此,α的值可以反映出离心泵扬程–流量曲线的稳定性[7]。
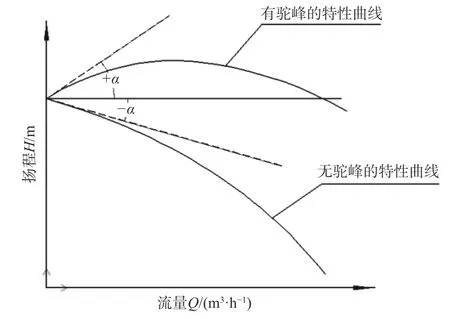
图4 离心泵的H-Q 曲线
3.2 正交试验结果及分析
用Ansys-Fluent17.0 软件,使用与原模型泵相同的模拟方法,得到16 组泵设计方案下的模拟结果。绘制各个模型的扬程–流量曲线,测量出各曲线的关死扬程点与水平轴的夹角 α,并得出设计工况点的扬程、效率和轴功率,试验结果如表4所示。
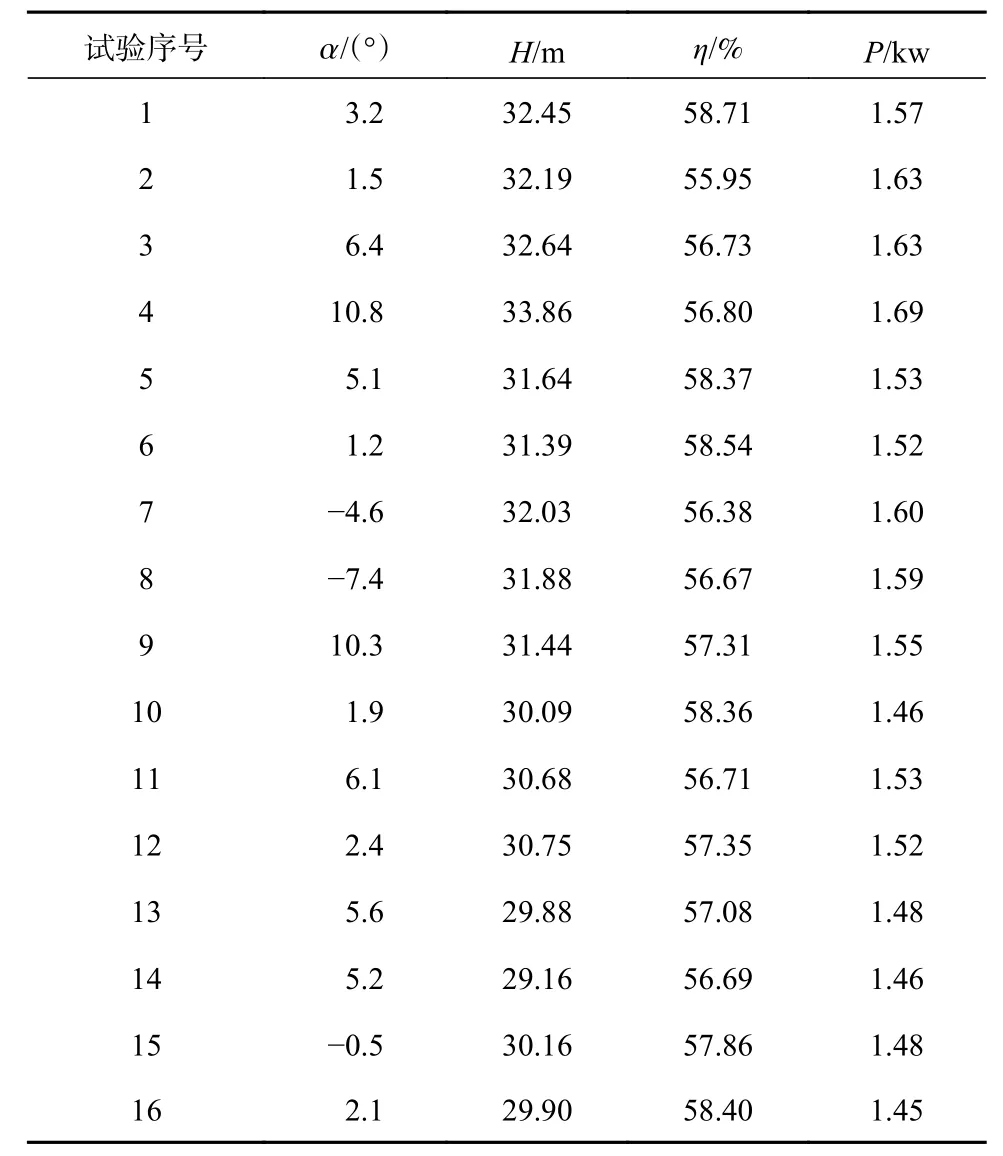
表4 正交试验结果
对正交试验模拟结果进行极差分析,如表5、6、7 所示。表中Ki为每个因素第i个水平的数值之和,ki为每个因素第i个水平的平均值,R为极差,反映了对应的因素对试验指标的影响大小,极差是这i个水平中的最大值与最小值的差值。通常情况下,因素的ki值越大,说明该水平下的稳定性、扬程、效率就越高。因素的极差R值越大反映出该因素对性能指标的影响程度越大,各个因素的R值不同,说明每个因素对性能的影响程度不同。
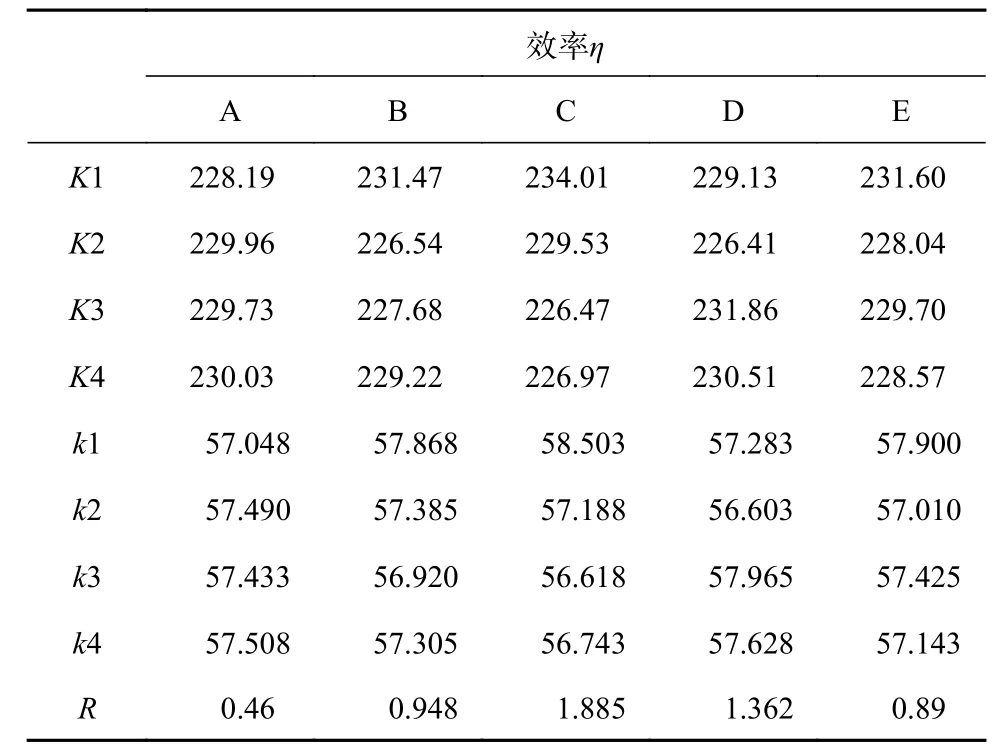
表7 效率的极差分析
由极差R分析可知,各个因素对扬程–流量曲线稳定性影响的主次顺序依次为E、A、B、D、C,即进口边位置前移、叶轮出口边斜切、叶轮轴面倾斜、叶片出口角、叶片包角。
根据各因素对关死扬程点与水平轴的夹角 α、扬程和效率的影响主次顺序可知,稳定性的最佳组合为A2B4C1D2E1,扬程的最佳组合为A1B4C4D4E2,效率的最佳组合为A4B1C1D3E1。由于本文的主要目的是提升低比转速离心泵特性曲线的稳定性,而叶轮出口边斜切、叶轮轴面倾斜和进口边位置前移对稳定性影响比较明显,对扬程、效率的影响不明显,出口角对离心泵扬程的影响明显,包角对效率的影响较明显,但是它们对稳定性影响相对较小,故最终的优化组合方案为A2B4C4D3E1,即:=0.96,θ=15°,β2=48°,φ=126°,d=22.7 mm。
4 优化模型的数值模拟验证
4.1 性能曲线对比
对优化组合方案所得的优化泵进行三维建模,并采用相同的方法进行数值模拟,得到优化后的模型泵的特性曲线,与原模型曲线进行对比,如图5所示。
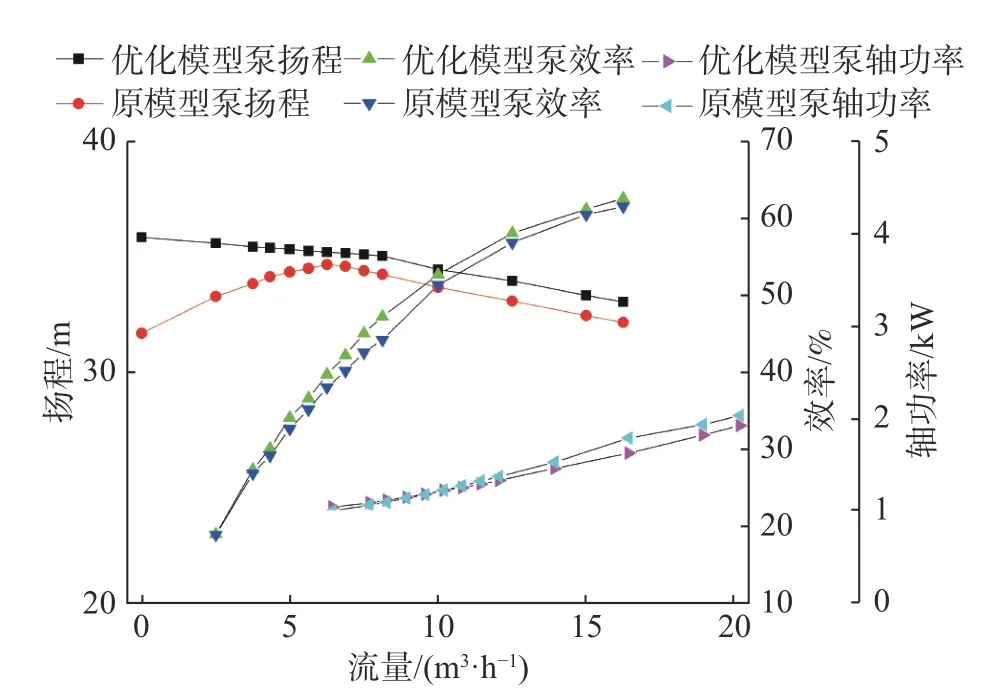
图5 优化模型泵与原模型泵性能曲线
由图5 可以看出:优化后的模型特性曲线稳定,效率普遍有所提升,轴功率略有下降;在额定工况12.5 m3/h 处的扬程和效率分别提升了2.2%和1.4%。可以发现,在叶轮叶片出口角很大(已达到48°)的情况下,通过叶轮出口边斜切、叶轮轴面倾斜、叶片进口边前移3 个因素的共同作用仍然可以设计出扬程–流量曲线稳定且高效的离心泵。
优化模型比原模型的整体性能提高很多,证明了正交试验的可行性,优化模型不在正交表内,也体现了正交试验的优越性。
4.2 叶轮内部流场及能量损失分析
4.2.1 叶轮静压分析
图6 为优化模型泵的叶轮与原模型泵的叶轮在0.6Q~0.4Q工况下中间截面静压分布图。
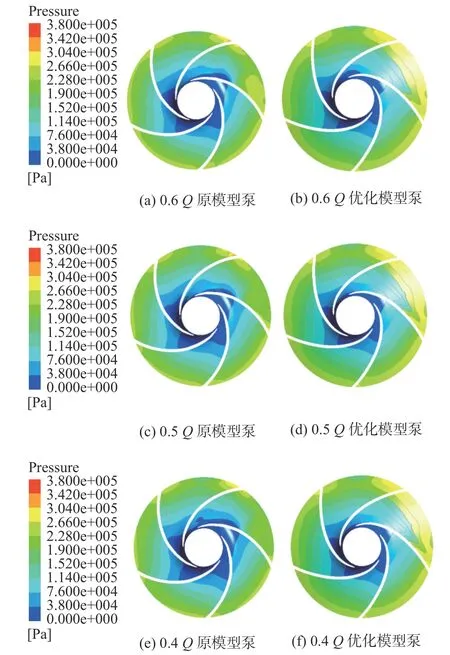
图6 原模型泵与优化模型泵叶轮静压云图
由图6 可以看出:流体经过叶轮进口通过叶轮流道,叶片做功能力不断加强,静压均由叶轮进口向出口递增,但优化模型递增明显更加均匀;在各个工况点处的进出口压差大于原模型,静压梯度变化更为明显,叶轮内的损失明显减小,但叶轮内的损失较为复杂,很难判断各部分损失的具体大小。
4.2.2 叶轮内损失的定量分析
为了能定量分析从叶轮进口到出口的能量损失,引入流线上的流体质点的转子焓(Rothalpy值)。对于叶轮内不可压缩的无黏流动,在不考虑叶轮内损失的前提下,Rothalpy 值沿同一条流线为常量,当考虑叶轮内的损失时,流线上两点之间该参数的差值就表示能量损失。定义Rothalpy 值为I,则I可以表示为
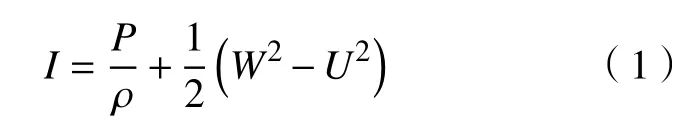
式中:W为流体质点的相对速度;U为圆周速度;P为静压;ρ为密度[10−11]。
由于原模型泵的驼峰发生在0.5Q工况处,故绘制如图7 所示的0.5Q与0.4Q工况下,通过公式(1)计算得出的近蜗壳隔舌处叶轮流道内中间流线上的Rothalpy 值沿着其位置的变化曲线。其中0 代表中间流线的进口起点,1 代表中间流线的出口终点,L表示中间流线的长度,L′表示中间流线的起点到该流体质点处沿中间流线的长度,利用L′/L可表示流体质点在流线上的位置。
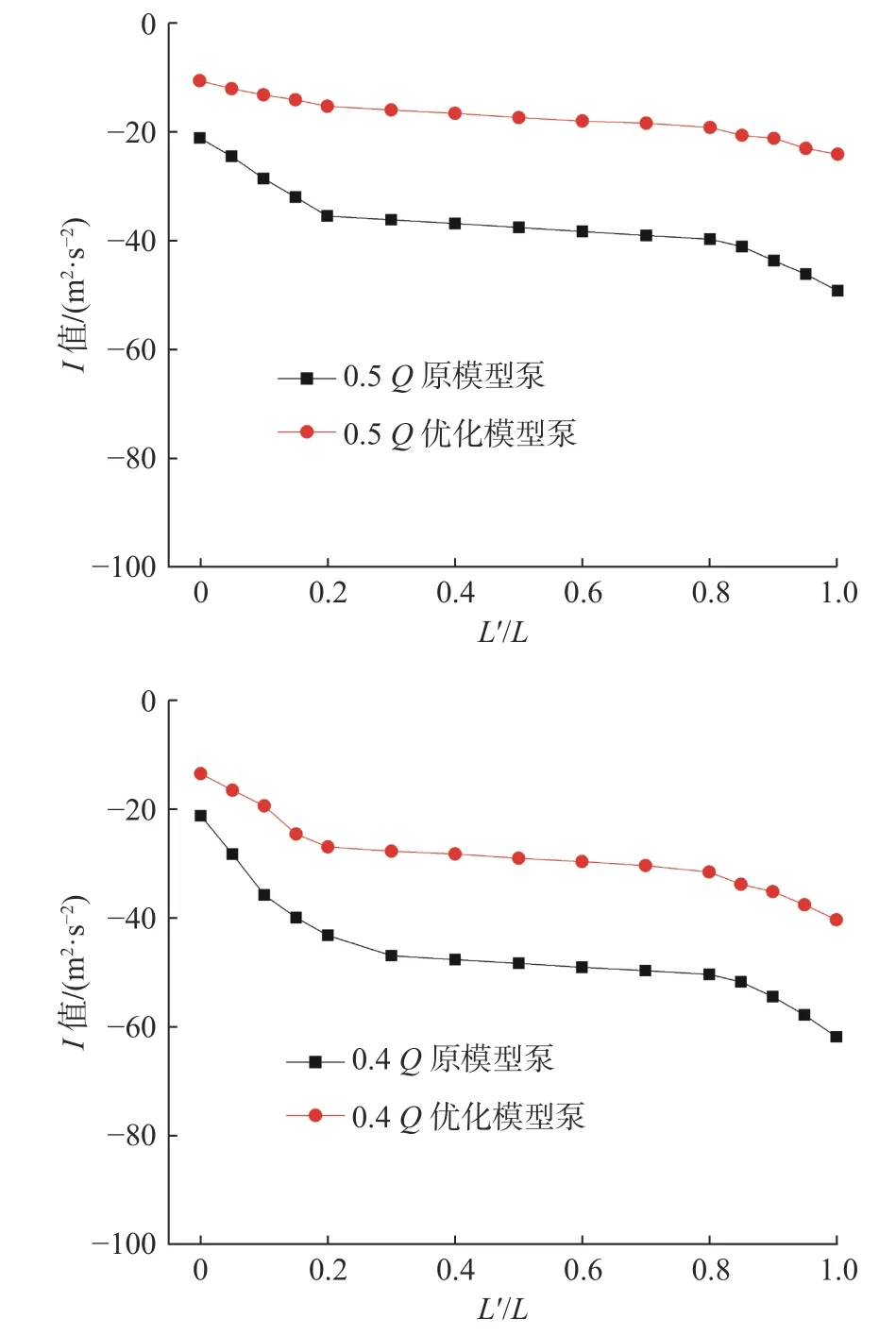
图7 叶轮内流线上Rothalpy 值变化曲线
由图7 的变化趋势可以看出,在叶轮进口附近(0—0.2),原模型泵在0.5Q和0.4Q的Rothalpy 值下降明显,整体分别下降14.93 m2/s2和20.72 m2/s2,并且在0.4Q时Rothalpy 值下降区域扩大至位置0.3,接近叶轮中间段。原模型泵在小流量区工作时,冲角的增大导致了进口处冲击损失的变大,而优化模型泵进口边靠近吸入口,进口角变大,流体进入叶轮内的冲角变小,冲击损失减小。在流道中间区域,由于流道内损失减小,Rothalpy 值下降缓慢。在叶轮出口处(0.8—1),原模型泵在0.5Q和0.4Q处的Rothalpy 值平均下降10.62 m2/s2和13.54 m2/s2。这是由于叶片流道前后出口处的相对速度变化过大,产生“射流–尾迹”现象,导致出口处水力损失增大。优化模型泵在0.5Q处与0.4Q处的Rothalpy 值下降较缓,整体下降14.82 m2/s2和27.16 m2/s2,其中在进口段与出口段的Rothalpy 值下降较中间段明显。这主要是因为在小流量区域内,由于冲角的增大,无法避免要产生一部分冲击损失。经对比,优化模型泵较原模型泵的水力损失减小,且进口段的损失在整个叶轮损失内占据主导地位。
为了定量地分析出口处相对速度的变化规律,在叶轮中间截面处的相对速度流场中,选择靠近蜗壳隔舌处的叶轮流道进行“射流–尾迹”分析,位置如图8 所示。由于优化模型泵的叶轮出口边斜切比例为0.96,为保证其位置在叶轮内部并靠近出口,取R=0.95R2。
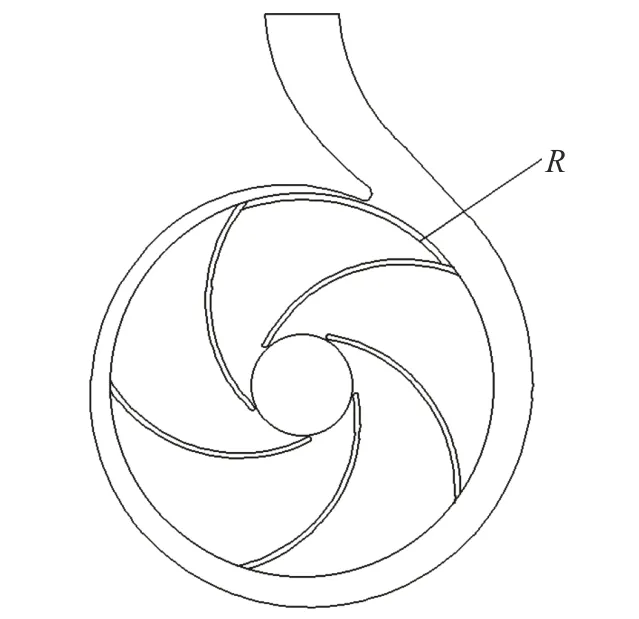
图8 叶轮出口处分析的流道位置
在图9、10 中,横轴中的0 代表叶片的压力面,1 代表叶片的吸力面,Ψ为该叶轮流道在以叶轮旋转中心为坐标原点的坐标系内在圆周方向上所占有的角度,Ψ′为该流道叶片压力面起点至流体质点在该坐标系内在圆周方向上所占有的角度,利用Ψ′/Ψ可以表示流体质点在流道中的位置。尾迹区为靠近吸力面速度较小的区域,其余速度较大的区域为射流区。由图可得到,优化模型泵流道出口处的尾流区很窄(约占20%),原模型泵流道出口处的尾流区较宽(约占55%),0.5Q工况下优化模型泵流道出口处相对速度最大值为5.163 m/s,最小值为3.52 m/s,差值为1.643 m/s,原模型泵流道出口处的相对速度最大值为5.757 m/s,最小值为3.014 m/s,差值为2.743 m/s。优化模型泵较原模型泵流道出口处的相对速度最大值和差值均减小很多,射流与尾迹间的速度梯度降低。结合图11 中在0.4Q处两模型的相对速度矢量图比较,认为改善的主要原因是优化模型叶轮出口处后盖板一部分叶片被切掉,叶轮轴面倾斜,导致后盖板一侧叶片做功能力变差,排出流体偏向外径大的前盖板一侧,后盖板侧的流体向前盖板移动,降低了出口处的相对速度梯度。优化模型泵在各个流量点处射流与尾迹过渡平缓,相对速度梯度小,水力损失小,所以优化模型泵的扬程–流量曲线稳定性获得增强。
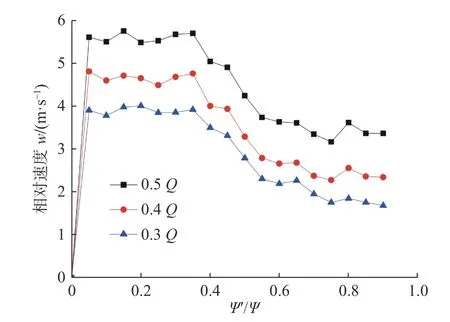
图9 原模型泵叶轮出口处相对速度变化
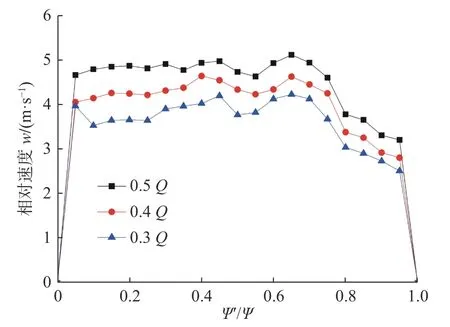
图10 优化模型泵叶轮出口处相对速度变化
5 结论
1)影响离心泵扬程–流量曲线稳定性因素的主次顺序依次是叶片进口边前移、叶轮出口边斜切、叶轮轴面倾斜、叶片出口角度、叶片包角。
2)通过分析各个因素对离心泵性能指标的影响,得到模型泵的优化方案,优化方案为=0.96,θ=15°,β2=48°,φ=126°,d=22.7 mm。优化后的模型扬程–流量曲线稳定,额定工况下扬程和效率分别提升2.2%和1.4%。通过叶片进口边前移、叶轮出口边斜切、叶轮轴面倾斜3 个因素的共同作用,即使在出口角很大的情况下仍然可以设计出扬程–流量曲线稳定且高效的离心泵。
3)驼峰工况区内,叶轮进口段的损失在叶轮损失内占据主导地位,出口段的损失次之。将进口边位置靠近吸入段,减小了叶轮进口的损失。采用出口边斜切、叶轮轴面倾斜,能使出口处的相对速度变化较小,“射流–尾迹”现象消失,出口处的损失降低,扬程–流量曲线较为稳定。

