改进组合差分定位算法在无人机上的应用

邸 健，杨国东，张旭晴

(吉林大学 地球探测科学与技术学院，吉林 长春 130026)

目前,全球导航卫星系统(GNSS)已经达到cm级的定位精度，差分定位技术被广泛用于高精度定位中[1]，一般测量型的差分GNSS系统具备高精度、高可靠性的优点，昂贵的价格以及较大的体积限制其普及。在无人机领域，很多微小型的无人机无法搭载测量级GNSS设备，为了降低硬件质量只能搭载轻型GNSS接收机。但是这种轻型GNSS接收机的单点误差在10 m左右，定位精度较低，同时随着无人机飞行速度的提高，定位精度将会进一步降低。

单频GNSS接收机的定位精度不及双频的主要原因是电离层的延时误差，但是在短基线的范围内，这种误差的影响较小[2]，因此，单频接收机完全可以实现高精度定位。目前针对高精度GNSS定位的研究越来越多，Takasu等[3]对低成本U-blox接收机与螺旋天线在RTK定位中的表现进行了评估，最终得出天线的质量是影响定位精度的主要因素；Odolinski等[4]通过实验发现U-blox接收机在模糊度解算和定位精度上可以与测量型的双频GPS接收机处于同一量级；Mongredien等[5]采用U-blox接收机和差分改正信息最终实现了短基线范围的cm级定位精度；杨光等[6]人探究了U-blox接收机搭载在固定翼无人机上的定位精度，同时融合BDS/GPS的差分定位算法，极大提高了定位精度；李江卫等[7]人通过对低成本单频U-blox接收机的BDS/GPS定向性能的分析，得出在动态定向精度上略低于高成本测量型接收机。

北斗导航系统(Bei Dou Navigation Satellite System，BDS)是我国自主研发的卫星导航系统，能够提供全天时、全天候和全球性高精度自主导航定位服务，系统将由35颗卫星布满MEO,GEO和IGSO 3种不同的高度卫星轨道，将于2020年完成布网[8-10]。鉴于GPS与BDS系统具有良好的兼容性，本文采用BDS/GPS组合的定位算法，对静态数据和机载动态数据进行研究。首先在静态定位中，使用BDS/GPS组合定位算法和GPS单一定位算法对GNSS数据进行PPK解算，从卫星可见数、PDOP值和信噪比等方面对U-blox接收机的数据质量进行对比分析；在机载动态定位中，采用BDS/GPS组合定位算法对数据进行PPK解算，并结合改进的LAMBDA模糊度解算方法，保证动态定位精度和可靠性，为无人机提供更加准确的位置信息。

1 无人机PPK原理

GPS动态差分后处理技术(Post Processed Kinematic，PPK)是利用同步观测的一台基准站接收机和至少一台流动站接收机对卫星的载波相位进行观测，两台接收机在一定范围内共有的系统误差基本相同。因此，通过实测坐标与该已知坐标之差求出基准点的共有系统误差，进而改正待测点的坐标值，最终获取待测点的精确坐标。相对于RTK实时定位而言，PPK最大的优势就是可以使用精密星历对数据进行后处理，从而提高定位精度[11]。

载波相位观测方程式为：

φ=λ-1[r+c(δtu-δt(s))-I+T]+N+εφ.

(1)

式中:I为载波相位测量值；λ为波长；N为整周模糊度；εφ为载波相位测量噪声量。

通过同步观测的基准站和流动站接收机记录卫星的载波相位观测量，然后在计算机中利用GNSS处理算法进行线性组合，最终形成虚拟的载波相位观测量，确定接收机之间cm级的相对位置。

2 改进组合差分定位算法

在较高精度的数据处理过程中，对于短基线载波相位模糊度解算，本文采用BDS/GPS组合定位算法，使用双差观测模型消除接收机之间的钟差和平台的刚性误差。考虑到数值稳定性，本文算法将每个历元的移动站天线位置状态重置为单点解来代替纯动态模型，避免滤波器的迭代，提高计算效率，结合改进的LAMBDA算法提高动态定位中固定解的比率，进一步提高定位精度。

2.1 融合BDS/GPS的PPK解算方案

GPS卫星导航系统的观测矩阵为：

(2)

对于北斗卫星导航系统，其观测矩阵为：

(3)

式中：λL1为GPS L1C的载波波长，λB1为北斗B1频点的载波波长。两者的形式及各个符号代表的意义相同，为BDS/GPS组合观测模型提供了很好的前提条件[12]。假设在某一历元下，接收到n颗北斗卫星和m颗GPS卫星，则组合观测模型：

(4)

式中：φ为卫星载波相位观测量，N为卫星载波整周模糊度，b为基线向量，采用BDS/GPS组合定位可以使接收机接收卫星的数量大大增加，尤其是在动态定位中BDS/GPS组合定位比单BDS和单GPS定位更加准确可靠[12]。

利用扩展卡尔曼滤波器(Extended Kalman Filter，EKF)，使用测量向量yk在历元tk处估计未知模型参数的状态向量x及其协方差矩阵P：

(5)

(6)

(7)

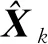
(8)

(9)

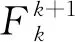
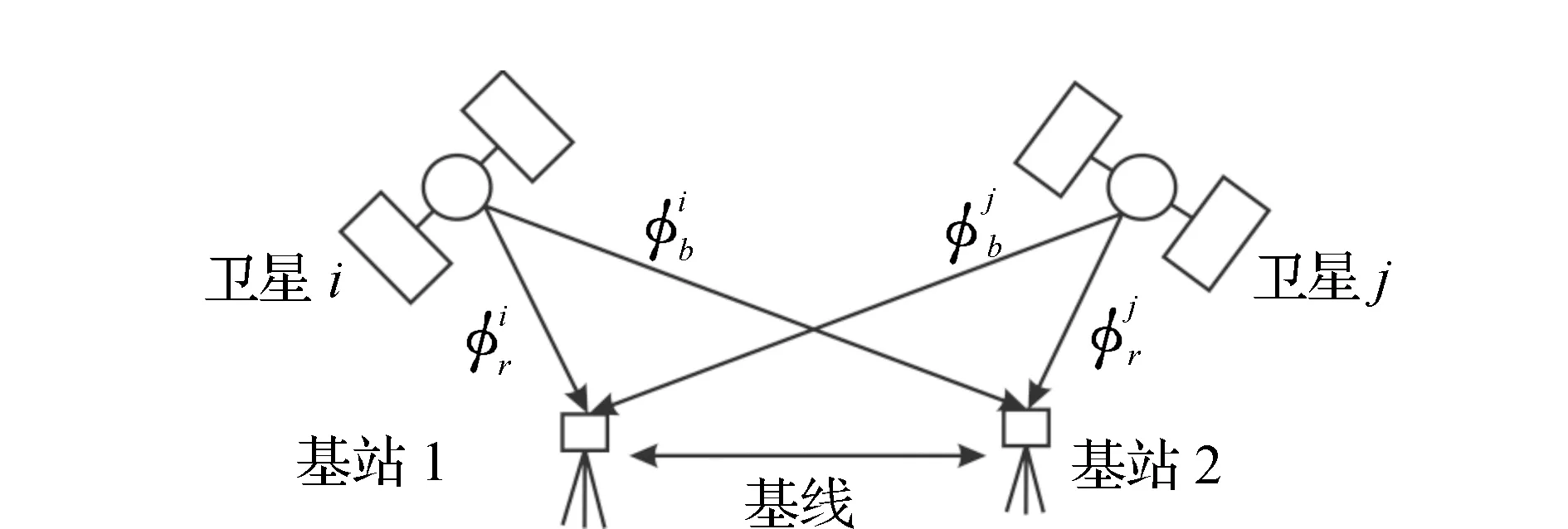
图1 双差模型系统阐述

(10)

(11)

GNSS差分定位中未知向量X定义为：

(12)

(13)

式中：r1代表地心固定坐标系(ECEF坐标系)下移动站天线位置。历元tk所对应的观测矢量yk包含伪距观测值和双差载波相位，具体表示：

(14)

(15)

(16)

(17)

(18)

Rk=

(19)

(20)

(21)

(22)

(23)

(24)

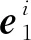
对于运动定位方式，通常假设移动站天线位置为白噪声模型：

(25)

为了保证数值的稳定性，本文算法将每个历元的移动站天线位置重置为单点解，进而代替纯动态模型，可以有效的避免非线性观测方程中的滤波器迭代计算，大大提高计算效率。本文采用的单一转换模型表示为F=I和Q=0，主要用于静态定位模型。同时采用无几何距离组合的周跳探测方法，通过式(5)可以估算移动站的位置和载波相位模糊度[13]。

2.2 基于LAMBDA算法的模糊度解算

在获得估算状态以后，为了提高定位精度和收敛时间，可以将浮点载波相位模糊度分解为整数值，首先将估计状态及其协方差矩阵转化为双差形式：

(26)

(27)

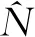
(28)

为了解决这个问题，采用LAMBDA算法及其扩展MLAMBDA算法[14]。LAMBDA和MLAMBDA提供了一个线性变换的组合来缩小整数向量搜索空间，并在转换空间中提供一个的搜索过程。通过简单比值检验，验证程序的整数向量解。在比值检验中，比值因子R被定义为次优解2n与最优解1n的残差平方和的加权和的比值，用来检验解的可靠性。验证阈值Rthres可以通过处理选项Min Ratio来设置，以修复模糊度。

(29)

验证后，通过求解以下方程获得移动站天线位置和速度的固定解。如果验证失败，将输出浮点型解决方案。

(30)

如果将处理选项设置为固定模式(整数模糊度解析=固定)，并且前面的测试验证了固定解决方案，则双差载波相位偏差参数受到固定整数值的严格约束。为此，RTKLIB向EKF输入以下伪测量值，并通过式(5)更新EKF。

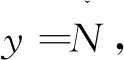
h(x)=Gx，

H(x)=G，

(31)

3 实例分析

3.1 研究区概况

实验区位于辽宁省铁岭市铁岭县，县域地处于东经123°28′～124°33′，北纬41°59′～42°33′，面积2 230.57 km2，见图2。境内地势走向呈现东高西低，东部为低山丘陵，海拔平均在200～300 m之间，西部为辽河冲积平原，地势平坦。本研究区域选择在铁岭县西南侧，平均海拔高度为70 m，数据采集时间为2020年4月8日，由于实验区当天风速较低，便于无人机飞行，且地势开阔，无高压线等遮挡物，保证飞行安全。

图2 实验区地理位置示意图

3.2 实验仪器及解算软件

所使用的仪器包括开源pixhawk飞控四旋翼无人机、U-blox NEO-M8T多星座接收机模块、四臂螺旋天线、三脚架、木桩等，使用软件包括mission planner地面站和RTKLIB2.4.3版本，其中mission planner地面站用于无人机的航线规划以及数据交互，RTKLIB用于BDS/GPS组合算法编写和精度分析。

其中NEO-M8T接收机的尺寸为5.5 cm×3.4 cm×1.2 cm，具有差分GNSS功能，可以输出原始观测数据，包括L1载波相位观测值。基站更新频率为1 Hz，移动站设置为10 Hz的采样频率。

3.3 地面静态定位试验精度分析

为测试该低成本高精度GNSS测量系统的性能和定位精度，设计三组不同的基线长度进行静态测量，分别是1 km、2 km和5 km，点位选取四周开阔无遮挡地域，将木桩钉入选好的点位10～15 cm，在其顶部设立观测点，保证坚固。将U-blox接收机天线紧贴观测点上部，保证天线的相位中心和观测点中心处于同一铅垂线上，连续观测1.5 h并记录数据。利用RTKLIB软件对所获取的原始数据进行PPK解算，对比GPS单一定位和BDS/GPS组合定位。结果如表1和图3所示。

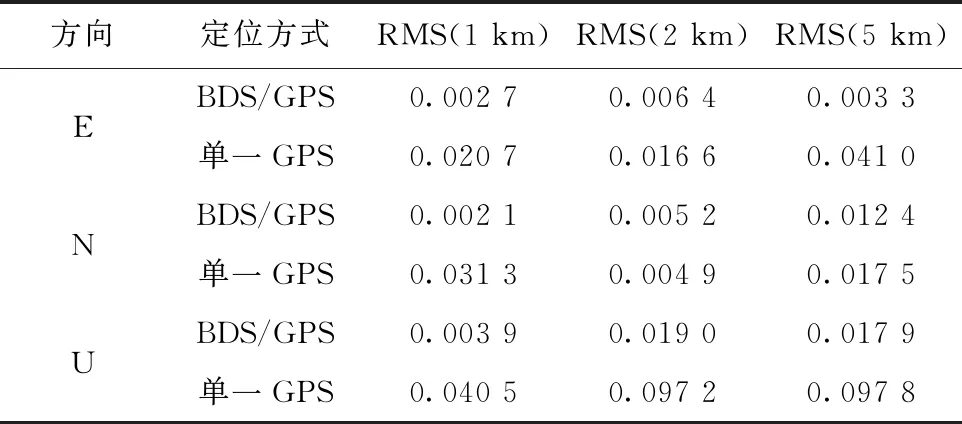
表1 BDS/GPS组合定位与单一GPS定位不同长度基线解算结果 m

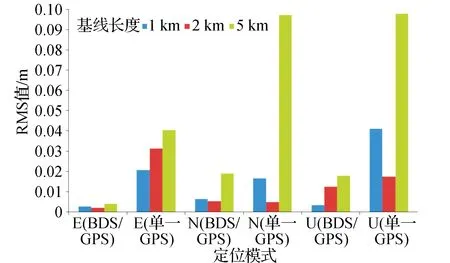
图3 不同定位模式解算结果比较

在基线长度为1 km的情况下，BDS/GPS组合定位精度优于1 cm，GPS单一定位精度优于4 cm；基线长度为2 km和5 km的情况下，BDS/GPS组合定位精度优于2 cm，GPS单一定位精度优于10 cm，组合定位的精度明显高于单一GPS定位，表明组合定位的定位性能稳定，定位结果更加精准。由此可见，本文所设计的GNSS系统定位稳定、精度较高。

3.3.1 卫星可见数

利用RTKLIB软件解算不同基线定位期间所能观测到的卫星数量和信号质量，在基线长度为1 km的情况下，BDS/GPS组合定位中共有10～25颗卫星用于定位观测，其中包括14颗GPS卫星和16颗北斗卫星，基线长度为2 km和5 km的情况下，BDS/GPS组合定位中共有8～25颗和11～24颗卫星用于定位观测，其中包括13颗GPS卫星和16颗北斗卫星，图4—图6表示所接收到卫星信号的连续程度，信号越连续表示接收的信号质量越好。表2为不同基线组合定位和单一定位的卫星可见数，从表2和图4—图6中可以明显看出BDS/GPS组合定位明显优于单一GPS，表明使用组合定位可以得到更加充足的观测量来进行数据解算，从而使定位精度更高。

表2 不同长度基线卫星可见数解算结果 颗

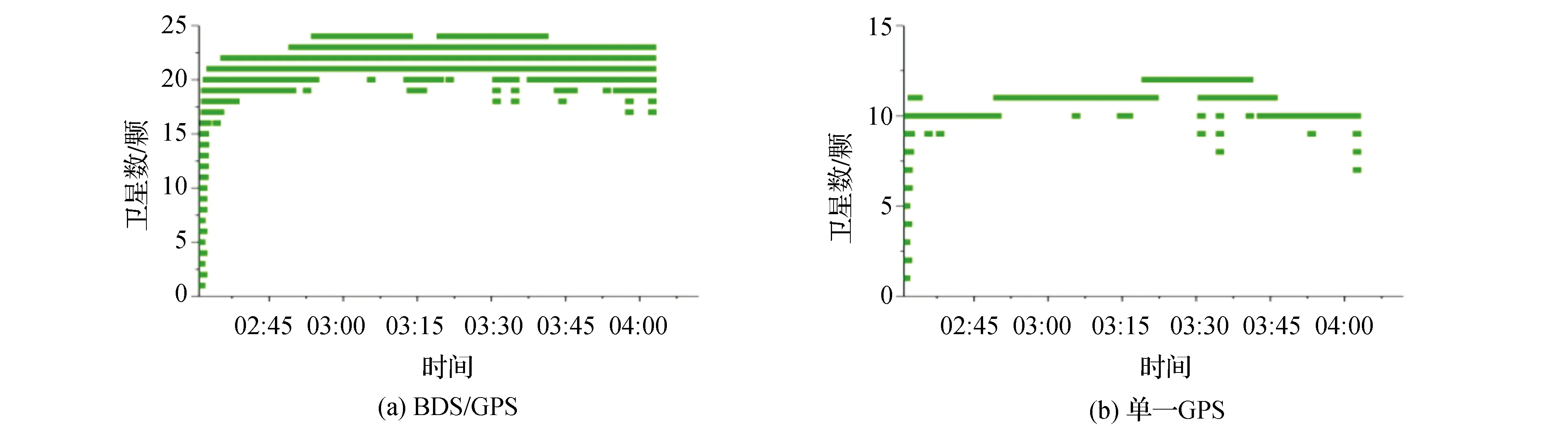
图4 1 km基线卫星可见数比较

图5 2 km基线卫星可见数比较

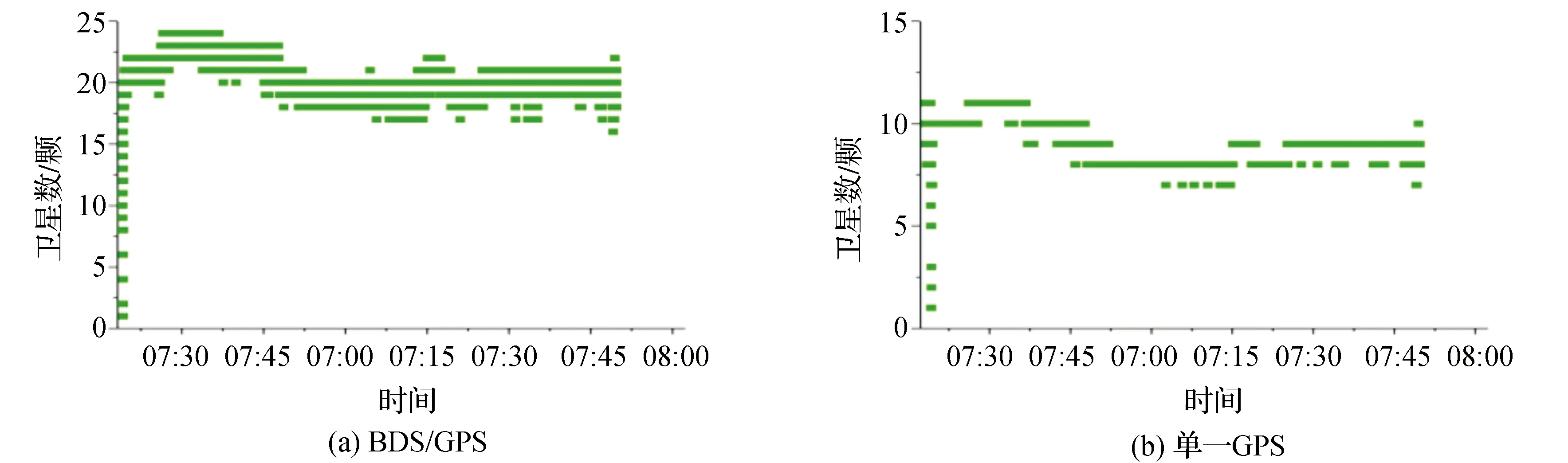
图6 5 km基线卫星可见数比较

3.3.2 PDOP值

PDOP(Position Dilution of Precision)代表卫星分布的空间几何强度因子，一般卫星分布越好，PDOP值越小[15-16]。在基线为1 km、2 km和5 km的情况下，经过RTKLIB处理后，由图7—图9可以看出，BDS/GPS组合定位的PDOP值在0.5～1.6平稳变化，GPS单一定位的PDOP值在0.7～2.6，组合定位的PDOP值明显低于单一GPS定位，表3为不同基线长度PDOP值，从表3及图7—图9可以看出BDS/GPS组合定位极大增强了测站与卫星的几何图形强度，因此定位精度将更加准确。

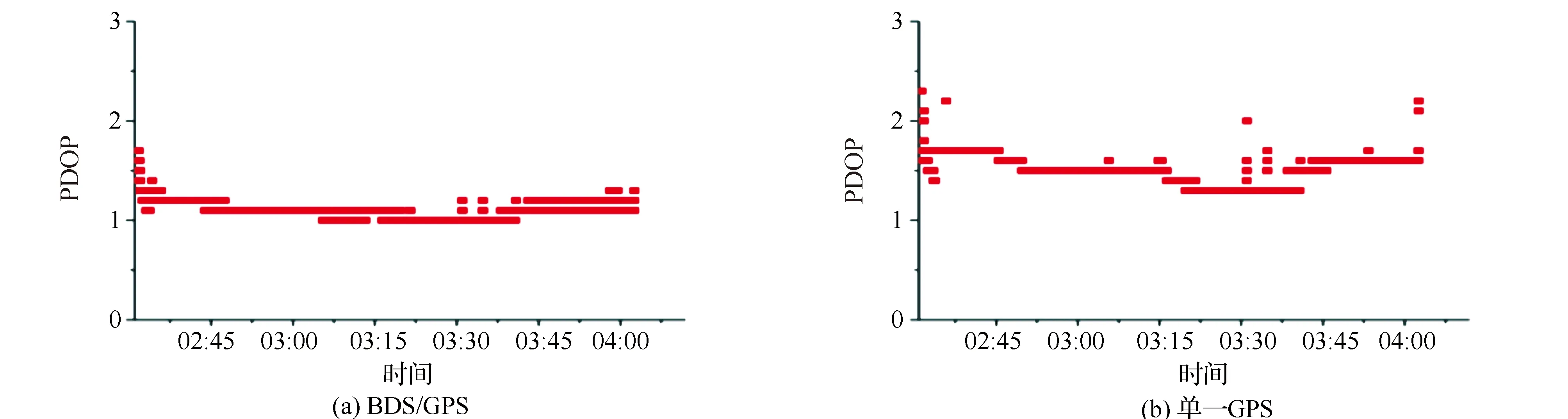
图7 1 km基线PDOP值比较

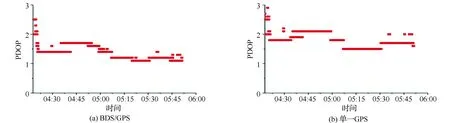
图8 2 km基线PDOP值比较

表3 不同长度基线PDOP值解算结果

3.3.3 信噪比

信噪比(Signal to Noise Ratio,SNR)表示接收机信号强度与噪声强度的比值大小，SNR越大，信号中的噪声越小，从而卫星的信号更好，定位精度更高[17-19]。经过RTKLIB输出(见图10)可得，在基线长度为1 km、2 km和5 km的情况下，BDS/GPS组合定位卫星的信噪比处于20～50 dB，其中绝大多数处于30～45 dB，表明卫星信号更强，定位结果也更加精准。

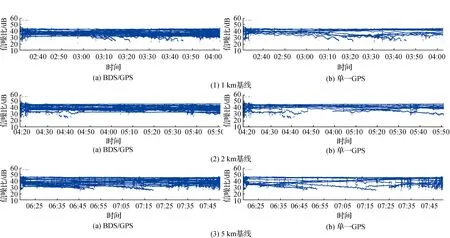
图10 信噪比比较

3.4 机载动态定位试验精度分析

无人机动态差分试验的组成部分如图11所示，用PC机存储原始数据，移动端搭载到pixhawk开源飞控无人机上。试验过程中基准站先开机，然后无人机通电打开移动站，静置10 min后开始工作。在mission planner地面站规划航线，此次动态试验共规划航线4条，相对航高100 m，飞行时间15 min。

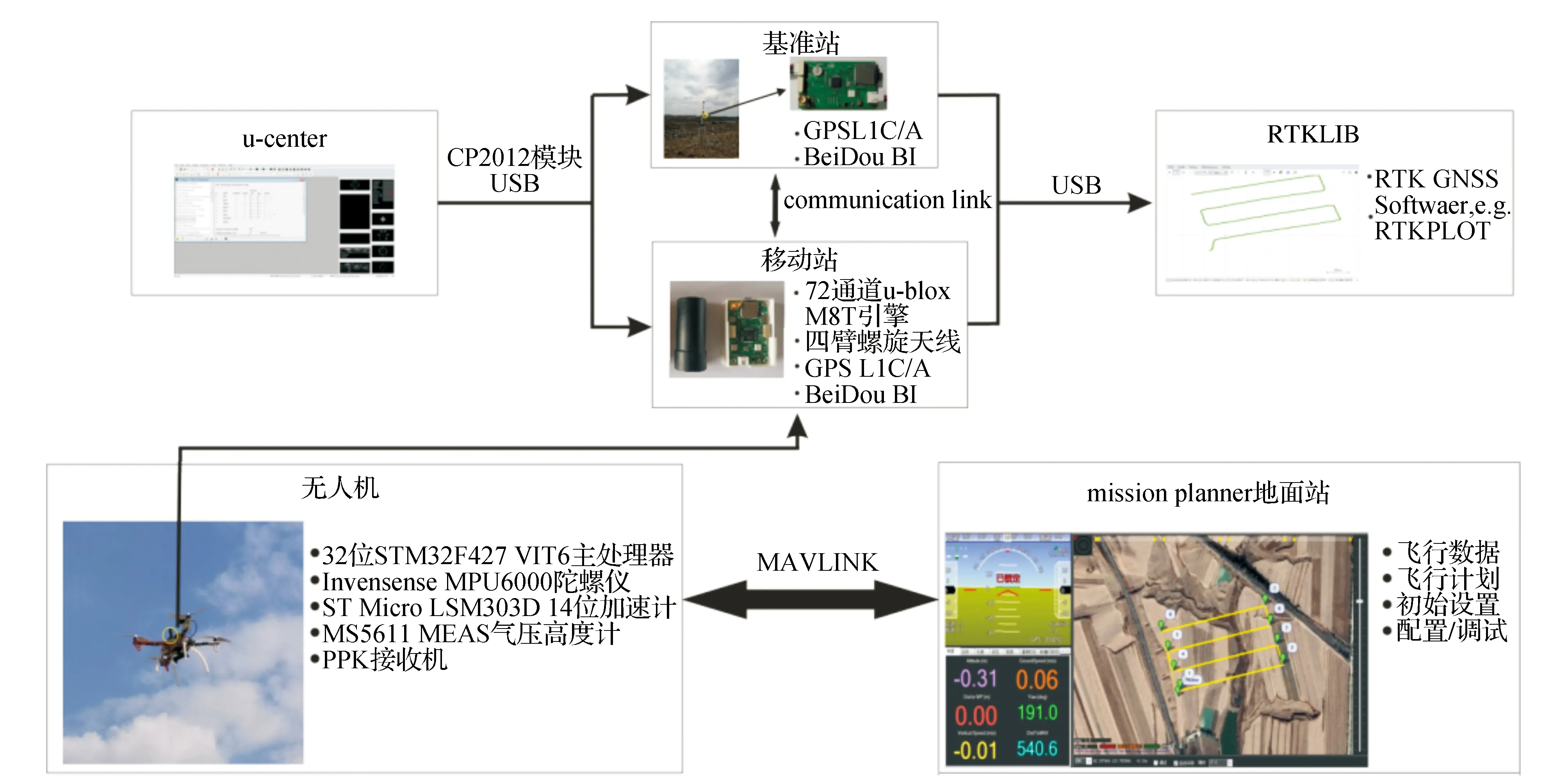
图11 机载动态定位实验结构图

从两种动态定位结果来看(见图12—图14)，在飞行速度一致的情况下，单点定位飞行轨迹与规划航线存在较大的偏差，而差分定位的飞行轨迹与规划航线吻合度较好，在高程方向上，差分定位高程波动范围较小，单点定位高程波动范围较大，定位精度较低。根据以上动态测试实验可知，差分组合定位精度远高于单点定位精度。

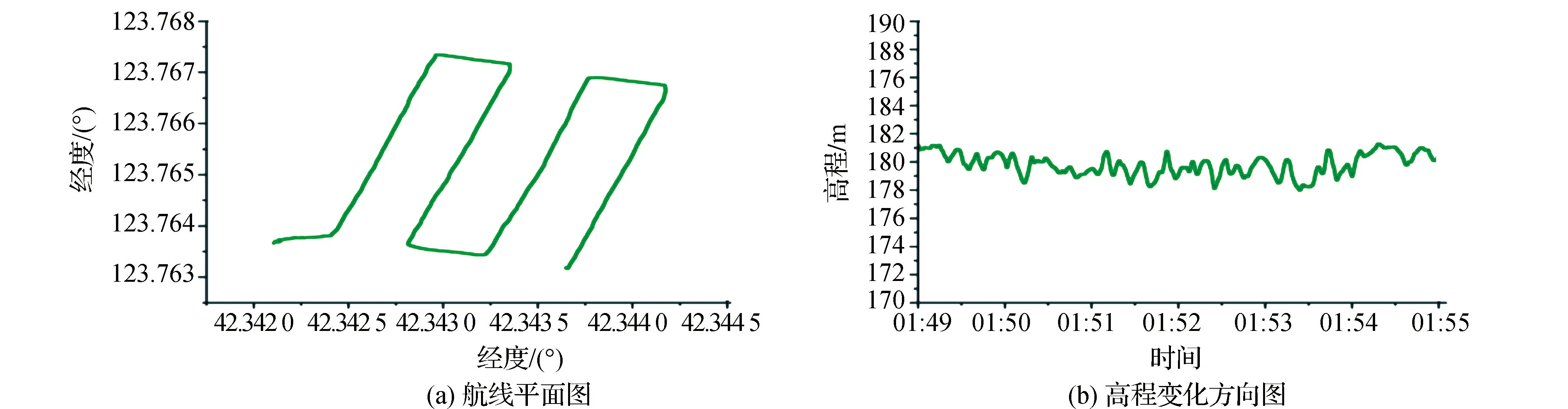
图12 差分BDS/GPS模式下无人机实验航线图

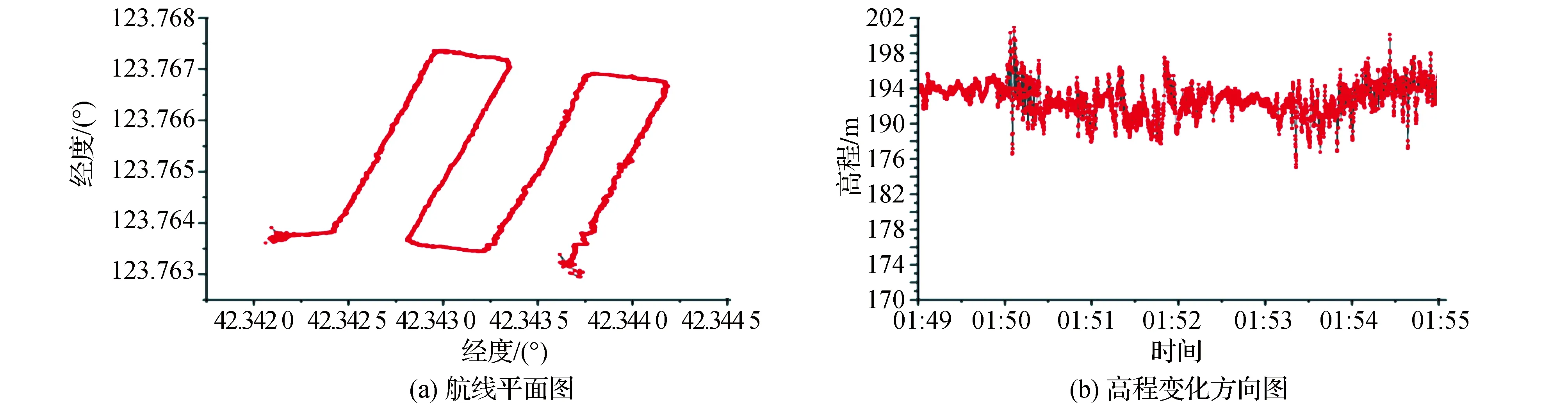
图13 单点BDS/GPS模式下无人机实验航线图

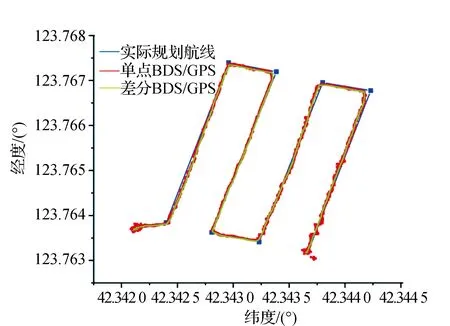
图14 两种定位模式的动态路径与规划航线的对比情况

试验发现，在数据解算过程中，传统的PPK模糊度解算方法获取的数据存在大量的浮动解，严重影响定位精度。如表4所示，采用改进的LAMBDA算法的模糊度解算方式对动态数据进行模糊度

表4 两种算法模糊度解算结果比率 %

解算。对比传统的PPK模糊度解算方法，结果(见表4)显示改进的LAMBDA算法将固定率从70.9%提高到96.3%。

目前商用消费级无人机多采用GPS/GLONASS组合算法进行定位，为了验证本文改进组合差分定位算法在无人机动态定位中的优势，采用NEO-M8T芯片，在研究区规划4条航线进行飞行，将GPS/GLONASS组合定位算法与本文定位算法所解算的数据进行对比。试验发现(见表5)，在水平飞行速度为4 m/s的条件下，BDS/GPS组合定位卫星可见数远高于使用GPS/GLONASS组合定位的卫星可见数，本文组合定位的PDOP值和信噪比也优于GPS/GLONASS组合定位(见图15和图16)。通过将本文定位算法和GPS/GLONASS组合算法所解算出的坐标数据与实际规划航线的对比分析得出，本文改进组合差分定位的精度明显优于GPS/GLONASS组合定位(见图17)。

表5 两种定位模式结果比较

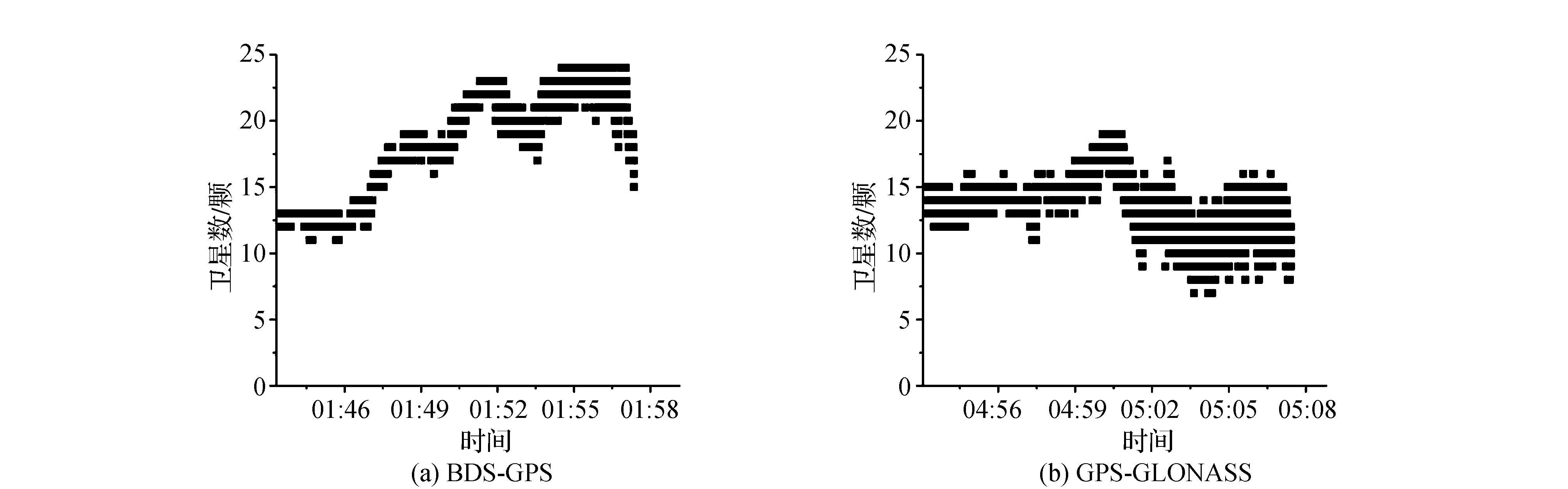
图15 两种算法卫星可见数比较

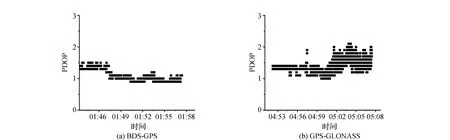
图16 两种算法PDOP值比较

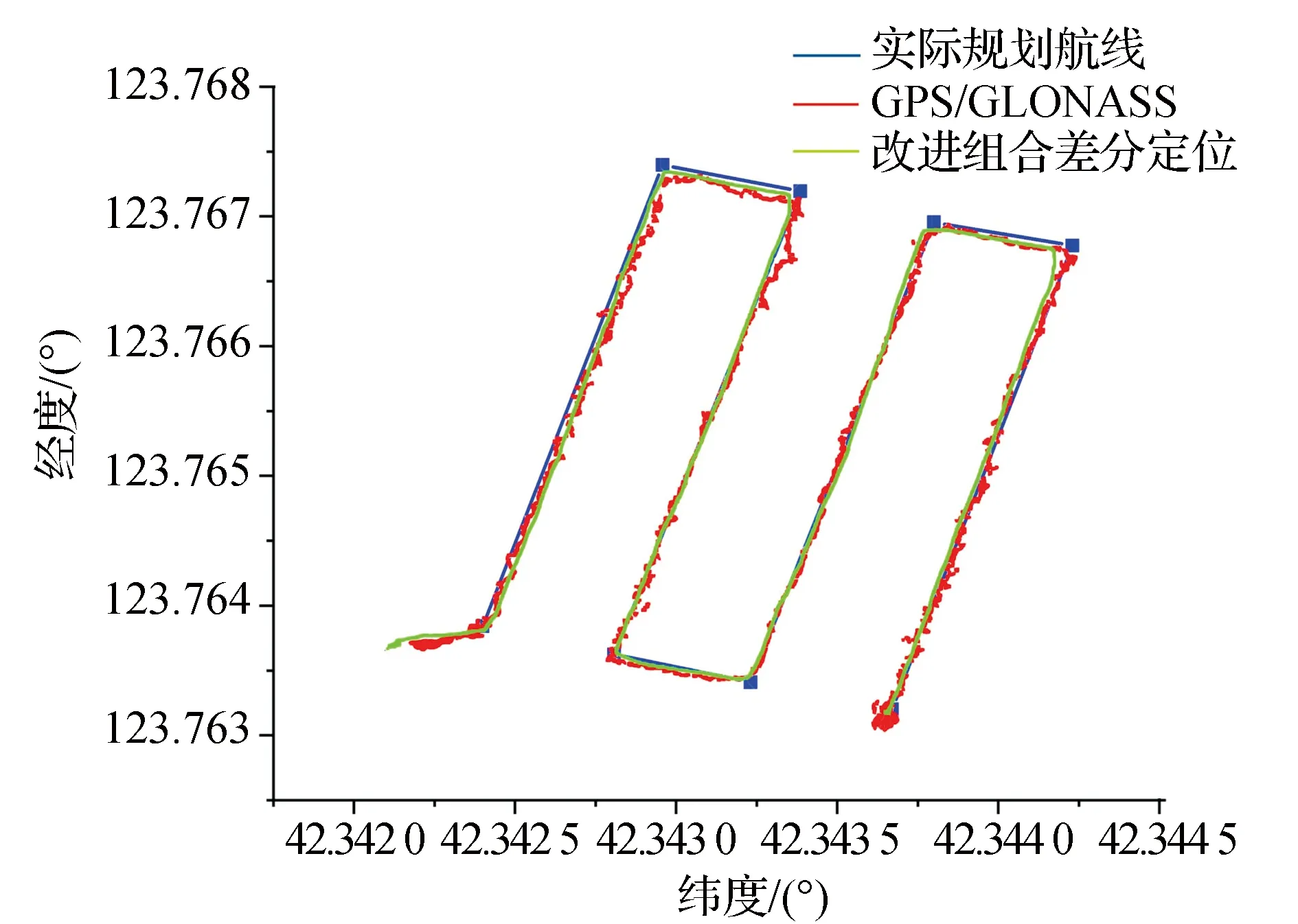
图17 两种算法的飞行轨迹比较

4 结束语

BDS/GPS组合定位可以提供更多的可用卫星，有助于改善卫星空间几何结构，提高卫星定位的观测精度。本文将BDS/GPS组合定位算法与改进的LAMBDA模糊度解算方法相结合，并利用实测数据对U-blox接收机的定位精度进行评估。结果表明，在静态试验中，BDS/GPS组合定位的卫星可见数、PDOP值和信噪比都要远优于单一GPS定位，稳定性较好，并且定位精度在cm级精度，在机载动态试验中，将两种算法相结合，动态定位数据固定解比率和精度大大提高。试验表明该微型GNSS PPK系统在无人机航测和精准定位等领域具有广阔的应用前景。