部分变量误差模型的极大似然估计

于子龙, 胡友健, 汪奇生，肖本林

(1.中国地质大学(武汉) 地理与信息工程学院,湖北 武汉 430078；2.湖北工业大学 土木建筑与环境学院，湖北 武汉 430068)

在测量数据处理中有些平差问题需要考虑系数矩阵的误差，如线性回归、坐标转换等，相应的平差模型称为变量误差模型(errors in variables, EIV)，EIV模型的参数估计采用总体最小二乘法[1]，近年来受到测量领域的广泛关注和研究，建立了相应的平差理论并得到了较多的研究成果[1-3]，从EIV模型观测值等精度情况下的总体最小二乘算法扩展到加权总体最小二乘算法[4]、非线性模型的总体最小二乘法[5,6]、观测向量与系数矩阵元素相关的总体最小二乘算法[7]、观测值含有粗差的稳健总体最小二乘法[8]、平差模型附有不等式约束的总体最小二乘算法[9]，以及贝叶斯估计的总体最小二乘算法[10]等。由于总体最小二乘最初的解算采用的是奇异值分解法，不利于测量领域的应用，特别是测量数据处理中通常要考虑观测值不等精度的情况。因此，关于EIV模型的加权总体最小二乘算法得到较多研究，相应提出一些迭代算法[11-22]。其中文献[15]提出了一种算法迭代格式与最小二乘间接平差类似的算法，算法简单，容易实现，而且迭代效率也较高。

由于EIV模型需要考虑系数矩阵误差，但实际平差模型中系数矩阵构造各不相同，可能同时存在随机元素和常数项的情况。常规的EIV模型加权总体最小二乘算法对系数矩阵常数项构造零权进行处理增加了参数估计的个数。文献[18]提出了部分变量误差(partial EIV)模型，只提取系数矩阵的随机元素项进行处理，较大程度的减少了参数估计的个数，简化了平差模型，但文献[18]提出的迭代算法迭代格式复杂且计算效率较低[19-22]。文献[19]提出了改进的迭代算法，但算法仍然复杂需要进一步简化[20]，而且没有验证算法的效果，通过实验发现其计算效率仍然较低。文献[20]针对这一问题，通过对平差模型的部分元素进行移项，通过两次间接平差，提出一种新的算法(文中称为算法1)，但新算法仍然存在收敛速度较慢的问题，通过进一步分析与文献[15]算法的关系，得到参数的另一种表达形式，提出一种迭代效率较高的算法(文中称为算法2)。但文献[20]提出的改进算法并没有从理论上进行严密推导，而且没有进一步分析文献[19]算法的关系。文献[21]根据非线性平差提出一种新的算法，算法迭代格式也有待进一步简化。文献[22]采用矩阵微分运算和矩阵反演推导一种新的算法，算法迭代格式其实与文献[15]算法也类似，但公式推导过程较为复杂。王乐洋还对PEIV模型的其他扩展算法和应用进行大量研究[23-26]。

鉴于此，为了进一步简化PEIV模型加权总体最小二乘算法公式，提高PEIV模型的解算效率，本文参照文献[10]的思路，采用极大似然估计方法进一步推导PEIV模型的高效迭代算法，该算法的迭代格式与文献[15]算法类似，易于理解和程序实现。并将本文算法与文献[18]算法、文献[19]算法以及文献[15]算法进行对比和分析，验证算法之间的等价性，最后采用两个算例进一步验证本文算法的有效性和可行性。

1 PEIV平差模型

PEIV函数模型为：

(1)

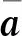
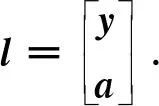
(2)

则平差模型的随机模型可以表示为：

(3)

不考虑系数矩阵元素与观测值之间的相关性，随机模型可以进一步表示为：

(4)

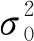
(5)

文献[18]提出的PEIV模型通过对系数矩阵的变换，只提取含有误差的项来进行处理，减少平差时待估参数的个数，但其提出的迭代算法效率并不高，收敛较慢且算法迭代格式复杂，Fang采用贝叶斯估计对EIV模型进行参数求解[10]，提出了迭代算法，但经过实验验证发现其迭代效率依然不高。因此，本文根据其思路，采用极大似然估计对PEIV模型参数求解进行公式推导，并通过进一步推导提出迭代效率较高的算法。

2 PEIV模型的极大似然估计

极大似然估计的原理，假设观测值服从正态分布，构建观测值的似然函数，使得似然函数取最大值，通过对似然函数求极值的方法来估计待求参数，根据式(2)、式(3)可知观测值的期望和方差可以表示为：

E(y)=(βT⊗Im)(h+BUa)=vec-1(h+BUa)β,

(6)

式中:Ua为系数矩阵中随机元素a的期望，vec-1表示的是矩阵拉直运算的逆运算即重构矩阵，根据式(6)，可构造观测值的似然函数：

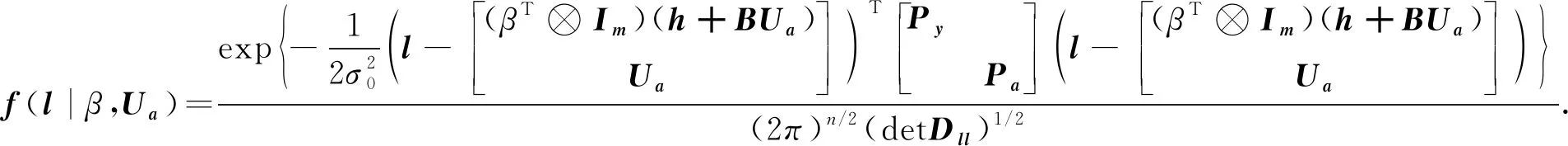
(7)

式中:含有两个待求参数β、Ua，极大似然估计的准则为对似然函数取最大值，即将分别对两个参数进行求导，并令其等于零。为了推算方便，对式(7)求对数仍然是等价的，进一步可以表示为：

lnf(l|β,Ua)=

(8)

将式(8)分别对两个参数求导并进行相应简化，可以表示为：

(9)

(10)

另式(9)等于0，可得到参数β的表达式：

β=((vec-1(h+BUa))TPyvec-1(h+BUa))-1×

(11)

参照文献[10]Fang的推导，本文不再赘述，令式(10)等于0，可导出观测值误差和系数矩阵元素误差之间的关系：

(12)

相应的顾及到ey+(βT⊗Im)Bea=y-(βT⊗Im)(h+Ba)=y-Aβ，则可进一步表示为：

ey=Qy(Qy+(βT⊗Im)BQaBT(βT⊗Im))-1×(y-Aβ),ea=-QaBT(β⊗Im)(Qy+(βT⊗Im)BQaBT×(βT⊗Im))-1(y-Aβ).

(13)

式(13)的表达式与文献[10]Fang的推导是等价的，根据文献[10]，则可以将迭代算法(本文算法1)表示为:

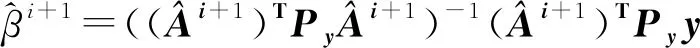
由于算法的推导和表达式与Fang基本相同，差别仅在于本文所述的是PEIV模型而Fang所述的是EIV模型，两者可以进行转换，因此将上述方法仍称为Fang法，其迭代格式与最小二乘相似，易于编程实现，但通过实验分析，Fang法的迭代效率较低，收敛较慢。通过上述推导可以发现，式(13)中仅仅用到系数矩阵元素的误差向量，而观测值的误差向量表达式并没有用来进一步推导，鉴于此，本文对式(13)进行进一步推导。结合上述推导，式(1)的第一式可以表示为：

y=(βT⊗Im)(h+BUa)+ey.

(14)

将式(13)中的ey带入到式(14)中：

y=vec-1(h+BUa)β+Qy(Qy+(βT⊗Im)×

(βT⊗Im)BQaBT(β⊗Im))-1(y-Aβ).

(15)

再将式(15)代入到式(11)中：

BQaBT(β⊗Im))-1(y-Aβ).

(16)

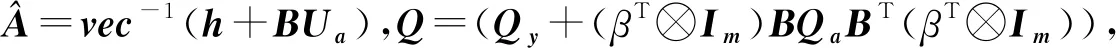
(17)

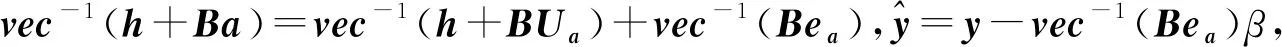
(18)

式(18)的参数求解公式，相对于式(11)利用了更多的信息，经过实验分析迭代效率有较大提高，另外，式(8)的迭代格式与文献[15] Jazaeri的EIV模型迭代算法是等价的，而本文基于PEIV模型更具一般性。

PEIV模型极大似然估计算法(本文算法2，为了方便在后文叙述中无特殊区分，所指的本文算法皆为本文算法2)的迭代步骤为：

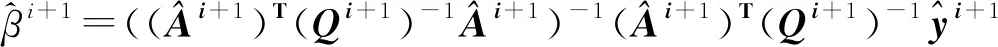
PEIV模型的单位权方差的评定公式为[18-22]：

(19)

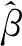
(20)

3 本文算法与文献中算法的比较分析

3.1 与Xu算法的比较分析

由文献[18]Xu提出的PEIV模型，相应的构建了PEIV模型的目标函数：

(21)

y}=0.

(22)

进一步可得到Xu算法的迭代公式：

β=(Nh+NB+NhB+NBh)-1(uh+uB).

(23)

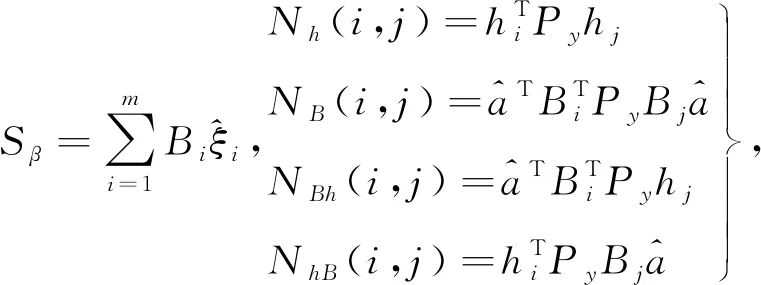
Xu在对式(22)第二式的β求解时，没有采用矩阵的拉直运算和重构矩阵运算，实际上式(22)第二式目标函数对β求导的表达式与本文式(9)是等价的，仅为表达形式不一样。其中式(23)第二式中(Nh+NB+NhB+NBh)=(vec-1(h+BUa))TPyvec-1(h+BUa)，(uh+uB)=(vec-1(h+BUa))TPyy，因此，Xu算法与本文所述的Fang算法是完全等价的。

3.2 与Shi算法的比较分析

在文献[19]中Shi提出了PEIV模型的改进算法，根据式(21)的目标函数对β求导并令其等于0，可得到参数β的表达式：

(24)

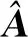
(25)

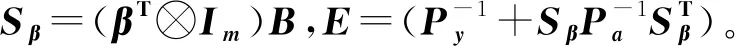
对比式(24)、式(25)与式(23)，Shi提出的表达式要比Xu的简化，但进一步比较可以发现，Shi提出的算法与本文所述的Fang算法是等价的，在迭代效率上并没有提高。对比式(24)与本文的式(11)可以发现，两个表达式是一致的。对比式(25)与本文的式(13)第二式，很明显也是完全一致的。因此，虽然Shi提出的迭代算法公式要比Xu的算法简单，但本质上并无差别，只是公式的表达式不一样而已。Shi提出的算法与Xu的算法都与本文所述的Fang算法等价，经过实验分析发现其迭代效率也基本一致。

3.3 与Jazaeri算法的比较分析

文献[15]中，Jazaeri提出的迭代加权总体最小二乘算法是基于EIV模型，其构造的目标函数为：

(26)

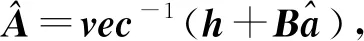
(27)

vec(EA)=-QA(β⊗Im)Q-1(y-Aβ).

(28)

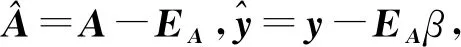
3.4 与Wang算法的比较分析

文献[20]中，Wang通过采用两次间接平差原理分别求解平差参数和系数矩阵元素，提出了一种算法(文中称为算法1)，平差参数和系数矩阵元素的求解公式为：

(29)

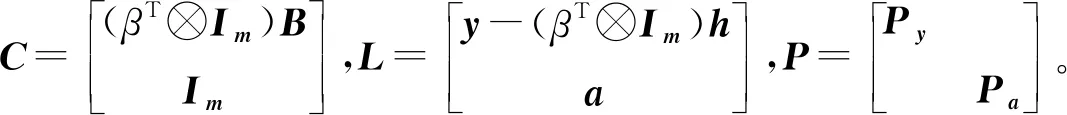
Pa)-1(BT(β⊗Im)Py(y-(βT⊗Im)h)+aPa)=

a+QaBT(β⊗Im)(Qy+(βT⊗Im)×

BQaBT(β⊗Im))-1(y-Aβ)=a-ea.

(30)

4 算例分析

4.1 算例1：二维相似坐标转换

为了说明算法的适应性，采用一个二维相似坐标转换的算例来进行验证，选用文献[15]中的坐标转换数据如表1所示，表中有5个具有原始坐标和目标坐标两套坐标系统的二维点，其相应的权值为：

Pxy=diag([18.781 7,6.377 4,12.648 9,17.476 9,22.272 6,23.982 3,13.680 4,3.465 6,3.732 4,6.437 7]);PXY=diag([9.831 6,5.535 7,12.736 9,12.009 9,10.181,11.366 1,11.147,5.883 4,9.832 2,7.567 8]).

用表1中的坐标数据来计算二维相似坐标转换参数，根据平差原理可知其也是一个典型的求解部分误差变量误差模型参数的问题。同样采用本文所述的Fang算法、本文算法、Jazaeri算法、Xu算法和Shi算法5种方法进行坐标参数求解，二维相似坐标转换的参数有4个，分别设为ξ1、ξ2、ξ3、ξ4，算法的收敛条件为δ=10-12，各算法估计的坐标转换参数结果列于表2，为了进一步分析各算法的计算效率，统计各个算法计算一次的迭代次数以及重复1 000次计算的总耗时和平均耗时列于表3，绘制几种算法在每次迭代过程中前后两次参数的差值范数于图1。为了比较各算法解算结果的差异，统计本文算法与其他算法参数估计结果的差值列于表4。

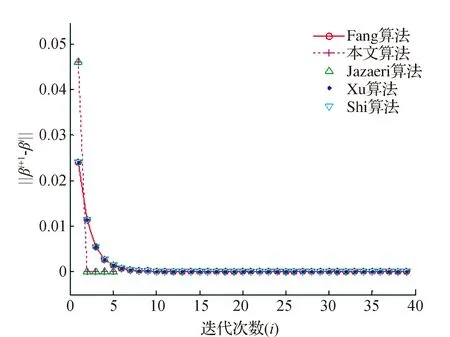
图1 各算法的迭代过程

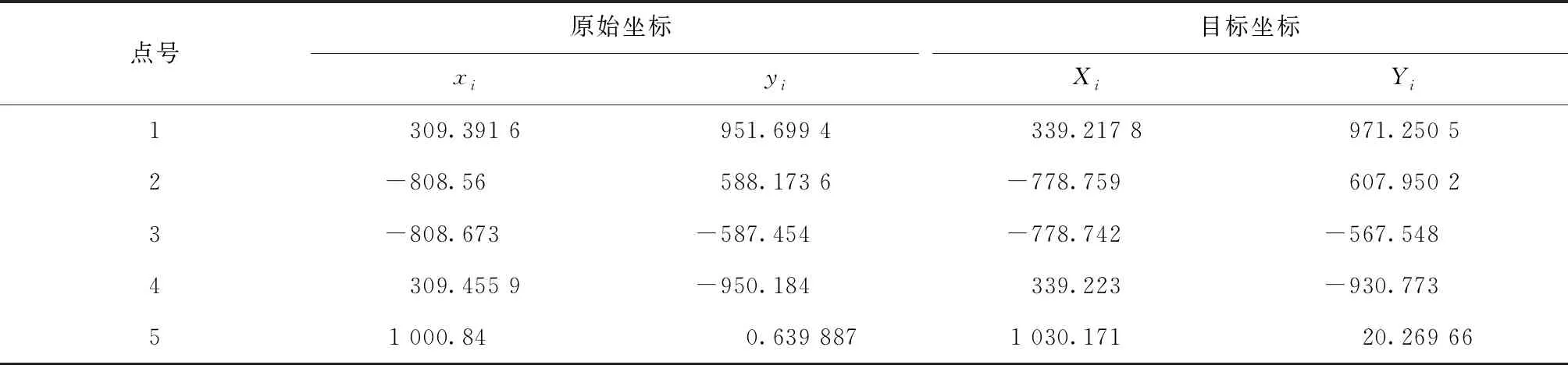
表1 原始坐标系和目标坐标系数据 m

表2 坐标转换各算法估计结果

表3 坐标转换各算法计算效率

表4 本文算法与其他算法估计结果的差异

从表2中可以发现，本文算法与其他几种算法得到的结果是一致的，这说明本文算法也能解算PEIV模型参数估计问题，从表3的计算一次的迭代数中可以发现，本文算法与Jazaeri算法的迭代次数一致且同样最少，其他3种算法迭代次数相同且较多，从1000次重复计算的总耗时和平均耗时可以看出，本文算法与Jazaeri算法接近且较其他3种算法要少，图1的参数迭代过程也清晰的表明本文算法与Jazaeri算法的收敛较其他3种算法要快，从表4的参数估计结果差异中可以看出，本文算法与其他算法解算结果差异最大都在10-12，少于本文迭代的收敛阈值，可认为各算法的解算结果是一致的，对比本文算法与其他算法的差异可以发现，与Jazaeri算法差异为0，这也进一步验证了本文算法与Jazaeri算法完全等价的结论；与Fang算法差异和Shi算法差异完全相同，这也说明了前文推导中两种算法是等价的结论；与Xu算法差异虽然与其他两种算法差异的结果不同，但差异值很小，可能是Xu算法采用的大量矩阵离散计算没有采用其他算法的矩阵拉直和重构而造成的差异，但都在本文的迭代阈值之内。综上说明本文算法在计算结果上能得到正确的值且计算效率具有一定的优势，进一步验证了本文算法的有效性和可行性。

4.2 算例2：二维仿射坐标转换

为了进一步验证本文算法的有效性，采用一个模拟的二维仿射坐标转换算例，算例引用文献[12]，13个具有原始坐标和目标坐标真值的二维点列于表5，二维仿射坐标转换的6个转换参数的真值分别为a1=0.9，b1=-0.8，c1=1，a2=0.6，b2=0.7，c2=5，根据表5的坐标真值模拟添加误差进行实验，本文在原始坐标和目标坐标添加的误差协因素阵分别设为：

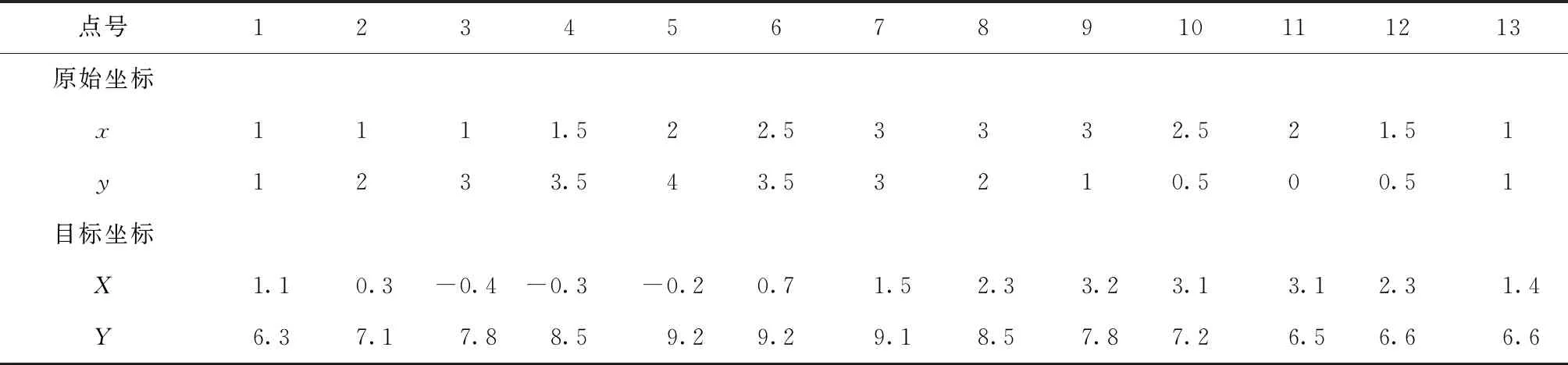
表5 二维仿射坐标转换数据

Qxy=I2⊗(0.005×diag([1,3,6,1,1,8,4,3,6,5,4,5,2]))，

QXY=I2⊗(0.005×diag([1,2,3,1,5,4,2,7,2,1,8,3,6])).

根据误差协因素阵共进行5 000次模拟，分别采用本文所述的Fang算法、本文算法、Jazaeri算法、Xu算法和Shi算法5种方法进行坐标参数求解，算法的收敛条件为δ=10-12，统计每一次模拟各种算法解算的结果，将各种方法获得的参数估计均值列于表6，统计各算法的平均迭代次数和迭代计算耗时列于表7，绘制5 000次实验中各算法的迭代时间于图2，统计本文算法与其他算法参数估计结果的平均差值列于表8。

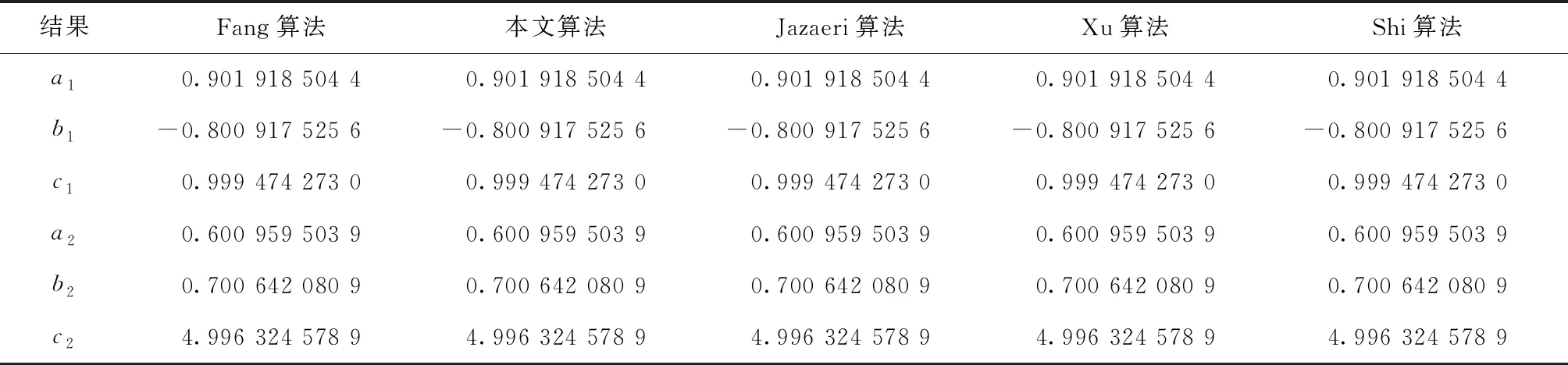
表6 二维仿射坐标转换各算法估计结果的均值

表7 二维仿射坐标转换各算法计算效率

表8 本文算法与其他算法估计结果的平均差异

图2 5 000次试验各算法的迭代时间

从表6的各算法计算结果中可以看出，本文算法和其他几种算法得到的结果一致，而且二维仿射转换参数的均值与真值比较接近，这说明本文推导的算法能得到正确的结果。从表7的算法计算效率中可以发现，本文算法与Jazaeri算法所需的平均迭代次数为9.077，相对于其他3种算法迭代收敛速度要快，这说明本文算法要优于其他3种算法，从迭代耗时上可以看出，本文算法与Jazaeri算法相对于其他3种算法耗时要少，而且本文算法比Jazaeri算法迭代收敛要快，这可能是因为本文算法采用的PEIV模型较Jazaeri算法采用的EIV模型在处理系数矩阵常数项时更方便，从图2的5000次试验各个算法的迭代时间中也可以说明本文算法相对于其他几种算法迭代耗时较少，迭代效率较高。从表8的本文算法与其他算法解算结果的平均差异中可以进一步说明，本文算法与Jazaeri算法解算的结果完全一致，在迭代公式上仅针对系数矩阵的处理上有差异，本文采用的是PEIV模型，而Jazaeri采用的是EIV模型，对于系数矩阵含有大量常数项的情况，本文算法处理起来更方便。对于其他3种算法，本文算法与它们的差异都在迭代收敛阈值之内，另外还可以发现与Fang算法差异和与Shi算法差异是完全相同的，这也验证了前文推导证明两种算法是完全等价的，仅在算法迭代公式的表述上存在一些差异。

5 结束语

PEIV模型只提取系数矩阵含误差的项进行处理，减少了常规EIV模型系数矩阵的估计参数个数，一定程度上简化了平差模型，但Xu提出的算法和Shi改进的算法计算效率较低且算法较复杂，本文基于极大似然估计原理推导了一种新的PEIV模型算法，该算法的迭代格式与最小二乘类似，易于理解和程序实现，通过与Xu算法、Shi算法以及Jazaeri算法的对比和分析，验证了算法之间的等价性，最后通过两个算例进行了分析验证，结果表明本文算法能得到与其他算法一致的结果，且算法迭代格式简单，计算效率较高。