也论形式主义与多宇宙观

杨睿之

什么样的数学研究是值得做的，什么样的数学定理是好的数学研究成果?这显然不是一个数学问题。但数学工作者对这个问题的看法无疑会影响他的研究志趣，进而影响他的具体工作，而数学家共同体对这个问题看法的分布则会影响数学这门学科的发展趋势。按照典型的形式主义数学哲学的解读，所有的数学研究都可以被看作是在某个给定的形式化公理系统中做证明。而一般认为，该公理系统的定理集是能行可枚举的（详见后文），即，存在一个计算机程序来枚举该公理系统所有可能的定理。然而，几乎没有人认为数学工作应该是这样的。即使利用程序辅助寻找证明，数学工作者也至少需要解读、挑选有意义的结果。因此，这个并非数学问题的问题却与几乎所有数学工作者的研究工作密切相关，难以回避。如果承认对该问题以及相关问题的回答并非完全主观任意，而是存在主体间就这些问题相互交流、考量、评判并形成共识的空间，那么数学哲学便是可能的了。

从早期以希尔伯特为代表的经典形式主义到科恩等人关于公理化集合论的形式主义，形式主义在现代数学哲学的讨论中一直在场。然而，自从哥德尔的两个不完全性定理的发现揭示希尔伯特形式主义原版的研究纲领不可实现，形式主义在严肃的数学哲学讨论中始终处于相对弱势的地位。尽管如此，形式主义对数学工作者仍然有着强烈的吸引力，尽管这一吸引力主要来自可以回避进一步的追问。正如Reuben Hersh写道：“典型的‘数学工作者’是工作日的柏拉图主义者，又是星期日的形式主义者。”[1]

集合论多宇宙观（set-theoretical multiverse view）是近年来兴起的区别于集合论单宇宙观（universe view）的集合论哲学观点。后者是数学柏拉图主义在集合论被广泛接受为数学基础这一语境下的具体实现，即认为存在唯一典范的集合概念以及由满足这一概念的所有集合组成的集合论宇宙，集合论语言中的任何一则命题关于这个集合论宇宙的描述要么是真的要么是假的。集合论多宇宙观则基于人们从构造内模型、力迫扩张及非标准模型以及在这些模型中“工作”的强健经验，宣称存在许多不同的集合概念或集合论宇宙。笔者曾在《集合论多宇宙观述评》中论证，集合论多宇宙观要么是一种形式主义，要么是与传统柏拉图主义或集合论单一宇宙观相容的[2]。

裘江杰在《集合论多宇宙观与形式主义》中试图把形式主义重新诠释为一种本体论中立的，并且有助于推动数学实践的数学哲学立场[3]。同时，裘江杰认为集合论多宇宙观可以被纳入这样一种形式主义立场，并且正是在这种形式主义的框架下体现出其对数学实践的正面影响。由此，进一步佐证了这种本体论中立的形式主义对数学实践是有益的。

在本文中，笔者试图挑战裘江杰的上述观点。在第一节中，笔者拟论证数学哲学的形式主义是无法真正做到本体论中立的。在第二节中，笔者将针对性地讨论形式主义就推动数学实践而言的局限性。在除去结论的最后一节中，笔者将结合一些新结果再次审视围绕集合论多宇宙观的集合论研究与有关数学哲学立场的关系，试图展现集合论多宇宙观独立于形式主义的价值。

一、形式主义不是本体论中立的

在《集合论多宇宙观与形式主义》中，裘江杰承接科里（Haskell Curry）的形式主义立场，认为形式主义应该是本体论中立的，它不在形而上学上做任何假设，并且形式主义并不拘泥于特定的形式化系统。特别地，他们认为形式主义不应该受到希尔伯特所谓有穷数学的掣肘。但这种形式主义仍然要求形式系统满足一定的可接受条件，其中包括一致性，却不要求一个一致性证明。此外，裘江杰和科里都认为关于这些形式系统的“元数学”研究是重要的。

在本节中，笔者首先试图论证任何有意义的形式主义都无法做到真正的本体论中立。同时，笔者也试图解释，希尔伯特关于形式主义“元数学”必须是有穷数学的限制性立场为何不能任意放宽。

在后人的解释中，一般认为希尔伯特的形式主义不是本体论中立的。他将数学分割为可靠的有穷数学（finitary mathematics）以及其一致性有待证明的经典数学，后者包括康托尔发明的集合论。的确可以说，希尔伯特本人关于包括集合论在内的经典数学的本体论问题试图展现一种中立的立场，或者说试图悬置抽象实体或无穷集合是否存在的问题。同时，希尔伯特捍卫数学工作者在“康托尔的乐园”中自由探索的价值，其手段就是将这部分数学形式化，并在可靠的有穷数学中证明这个形式化了的公理系统是一致的。这就是所谓的希尔伯特纲领（Hilbert’s Program）。我们知道，希尔伯特纲领因为哥德尔不完全性定理而注定无法在其原本意义上实现，但是希尔伯特形式主义乃至后哥德尔定理的希尔伯特形式主义变种在本体论上对数学进行区分的做法是一以贯之的。希尔伯特式的形式主义可以悬置那部分需要通过形式化方案来捍卫的数学的本体论问题，但要求对这部分数学的形式化给出一致性证明。这一立场意味着他们必须认为其所期望的一致性证明是可靠的，或在某种意义上是真的。无论这种一致性证明是基于有穷数学或其他构造主义数学的证明，他们必须或假设或尝试论证这部分数学是有意义的，它们对应着某种可靠的信念或具体的客观概念。

例如，竹内外史在《证明论》中为ε0下归纳原理所作的辩护①ε0是一个可数无穷的序数，它是序数序列ω,ωω,ωωω……的极限。根岑（Gerhard Gentzen）基于ε0下的归纳原理证明了皮亚诺算术的一致性。这被认为是希尔伯特纲领在哥德尔定理之后最重要的成就，也是现代证明论的开端。参见Takeuti G.,Proof Theory,2nd ed.,New York:Dover Publication,2013,第11节。。他定义了序数的可及性（accessible）概念来描述人们可以“切实地看到”或“构造性地证明”可及序数下的每个严格下降链都是有穷的。他试图论证，可及性在序数加法、乘法甚至幂运算下保持不变，从而证明ε0下的序数都是可及的。竹内外史宣称基于可及序数下的归纳原理相比完全的集合论是有穷主义的，相比直觉主义中抽象的“构造”“证明”概念又更加具体。因而，这是所谓“希尔伯特—根岑有穷主义立场”可以接受的数学命题。

再如，哥德尔对他的T系统的辩护。在《论一种迄今未用过的有穷主义观点的扩张》中，哥德尔描述了一个扩张了有穷主义限制的系统T，并证明了直觉主义算术相对于该系统的一致性[4]。哥德尔试图让读者相信，T系统基于的“自然数上的有限类型的可计算函数”概念是一个相比ε0更具体的、“意义清晰的”概念。读者可以在《哥德尔在构造主义数学方面的工作》中找到简要的介绍[5]。

在希尔伯特形式主义及其变种中，数学被划分为可靠的部分与“理想”的部分。这种立场的支持者有义务澄清划分的具体位置，并为这种划分辩护。对划分的辩护可能暗含在对可靠部分可靠性的辩护中。这种“区别对待”本身揭示了形式主义者对关于“理想”数学的本体论地位的看法，它显然不是中立的。

前希尔伯特的形式主义者或许可以声称他们对所有数学一视同仁。一些前希尔伯特的（往往是非自觉的）形式主义立场的确没有对数学做类似的划分，它们断言所有数学都是无意义的。例如游戏形式主义，认为数学工作者只是根据给定的游戏规则进行操作。但即使极端的游戏形式主义者也不得不承认，关于他们所玩的游戏规则是否和谐的问题是有意义的。人们显然不会认为，一个已知走某步就定胜负（如证明出矛盾从而可以证明所有命题）的游戏是值得玩的。而在希尔伯特之后，人们逐渐厘清了那些数学游戏的规则，形成了明确定义的数学公理系统，并借助于哥德尔编码等技巧，将关于游戏规则的问题明确地翻译成了对应的算术问题。正如人们很难拒绝承认图灵机可计算是对能行可计算概念的正确刻画。一旦这样的工具出现在眼前，人们就很难再拒绝承认这些翻译的正确性，这些关于游戏规则的问题就是数学问题，而且这些数学问题是有意义的。因此，希尔伯特式的形式主义对数学基于本体论地位的划分对一般的形式主义而言也是难以避免的。

或许，形式主义者可以声称所谓的本体论中立仅仅是指“理想元”部分的本体论中立。例如，作为哥德尔定理之后的形式主义者，科里不要求对公理系统的一致性证明。因此，也不需要承认一个用以证明一致性的具有更高本体论地位的“元数学”，尽管他仍然认为一致性是形式系统重要的属性。

希尔伯特所强调的正是一致性标准。这样做的原因大概是他……在寻找一个先天的合法性证明。但是，且不论对物理来说，一个先天的合法性证明的问题是不相关的，我坚持认为一个一致性证明既不是可接受性的必要条件也不是充分条件。它显然不是充分的。至于必要性，只要没有不一致性被认识到，一个一致性证明尽管带给我们关于系统的知识，但并不改变它的有用性。即使不一致性被发现，这也不意味着这一理论被完全抛弃，而是意味着它的修改与提炼……因此，希尔伯特在关于一致性方面的这一奇怪的立场并不是数学形式主义观念的一部分。[6][7]166

科里不要求一个先行的一致性证明，这是对自弗雷格以来人们探索数学基础基本动机的忽视。人们希望为数学寻找一个安全的基础，或是逻辑或是形式化的公理系统，以避免可能的谬误。弗雷格作为典型的实在论者可以不像希尔伯特那样寻求一个有穷数学的一致性证明。因为在他看来：“公理不会彼此矛盾，因为它们是真的；而这不需要一个证明。”[8]这里的证明是指希尔伯特在《几何基础》中给出的相对一致性证明或是基于有穷数学的一致性证明。显然，一则数学命题（在弗雷格看来是这则命题所表达的思想）作为公理仍然是需要辩护的，正如他在《算术基础》中所做的工作那样。无论希尔伯特的形式主义纲领、布劳威尔及其后继者的直觉主义宣言还是引领当代集合论研究的哥德尔纲领都继承了自弗雷格以来的这一诉求。科里诉诸物理学的比较来说明先天合法性证明是不需要的。然而在早已数学化了的物理学中，对一致性的辩护显然是必要的。任何物理学理论被要求与其他理论和已知现象一致。例如，关于量子力学标准模型一致性的讨论[9]。正是由于量子力学与广义相对论之间显然的冲突，人们清楚地意识到一个涵盖所有四种基本力的万物理论尚付阙如。因此，寻找一个兼容量子力学与相对论的一致的理论始终是理论物理学的核心问题。的确，无论在物理学还是数学实践中，人们往往（甚至注定）是在某个理论的一致性证明或其他“安全保证”尚未确立的情况下工作于其中的。但这不妨碍这类基础问题始终是数学、物理及其哲学的核心关切。而只要直面这一数学基础问题，无论柏拉图主义者、直觉主义者还是形式主义者（正如前文所分析的）都无法做到所谓的本体论中立。

关于科里的形式主义立场，一个有趣的事实是，他非常重视关于形式系统的“元数学”，甚至以此为数学的本质：“数学是关于形式系统的科学”[10]。他所关注的“元命题”主要是关于形式系统本身（诸如“命题x 是在形式系统X 中可证的”），以及形式系统之间关系（诸如，一个系统是另一个系统的子系统）这样的命题。而“形式系统X 是一致的”无非是某个具体的谬误（如0=1 或α∧¬α）“不是在形式系统X 中可证的”。因此，无论科里对系统一致性证明持有怎样的看法，他对所谓“元数学”地位的特别关注使他无法避免本体论上的二分立场。事实上，在关于数学的“形式主义”定义中，科里明确将“非构造性命题排除在真正的数学的领域之外”。因为，“这些命题的真取决于与构造主义命题中所蕴涵的形式不同的理想假设。”[10]56

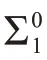
科里在关于什么是“元数学”的界定中，的确还留下了进一步解释的空间。他认为“涉及关系到外在（extraneous，相对于形式系统本身而言）考量或无穷主义假设的元定理，例如对塔斯基和哥德尔关于一阶谓词逻辑完全性证明的语义研究”[10]也可以被算作元数学。笔者未能在科里的著作中找到关于这类元定理的明确例子。我们知道哥德尔完全性定理需要至少在二阶算术语言中陈述，并且可以在二阶算术公理系统WKL0中被证明。另一方面，我们不能无限扩大对这部分“元数学”的解释。一般被认为，下行的勒文海姆-斯寇伦定理是哥德尔完全性定理证明的推论。但其证明中使用了某种形式的选择公理。准确地说，在ZF 基础之上，针对可数语言的下行的勒文海姆-斯寇伦定理与依赖选择公理（dependent choice，DC）是等价的；而针对任意基数语言的下行的勒文海姆-斯寇伦定理与选择公理等价[11]。显然，科里不会承认选择公理是否为真也是他所谓的关于形式系统“元数学”的问题。

二、形式主义对数学实践的影响

笔者在《结构主义是一种有效的数学哲学吗？》中质疑结构主义是有效的数学哲学[12]。在同样的意义上，形式主义无疑是有效的数学哲学。希尔伯特的形式主义纲领直面数学工作者的困惑。无论是希尔伯特本人关于几何的公理化工作，还是一阶谓词逻辑和集合论的公理化，抑或前文提到的根岑和哥德尔关于皮亚诺算术的一致性和相对一致性证明，都是在希尔伯特形式主义纲领启发下的数学工作。在这个意义上，形式主义的确对数学实践有着积极的影响。

裘江杰在《集合论多宇宙观与形式主义》中认为，元数学“作为对数学的反思性研究”是“形式主义的重要组成部分”，并且形式主义，尤其是被纳入形式主义框架的集合论多宇宙观有助于为集合论搜寻新公理。本节中，笔者则试图说明：形式主义者尤其关注的元数学研究恰恰非常依赖超出形式主义的思想和直观；而形式主义对探究集合论新公理的作用是有限的。

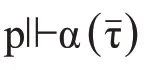
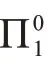
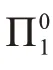
（1）∀xφ(x)蕴含{σi:i∈We}=ZFC；

（2）ZFC+Con({σi:i∈We})⊢∀xφ(x)。

这里我们援引递归论中的术语，用We表示编码为e 的图灵机的定义域，或“第e 个递归可枚举集”。我们说，ZFC 是一个递归可枚举的（实际上是递归的）公理集，也即存在一个自然数d 使得ZFC={σi:i∈Wd}。所以事实陈述中的{σi:i∈We}=ZFC 实际上是We=Wd这样一则一阶算术命题。此外，Wd又可以被表示为一个递归函数δ的值域：Wd={δ(i):i∈N}。

事实的证明假设ZFC={δ(i):i∈N}。我们可以构造一个部分递归函数Φe：

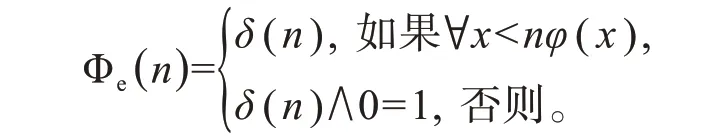
验证（2）：我们在ZFC中工作，如果¬∀xφ(x)，那么We中就包含0=1。因而，¬Con(We)。证毕。

科里认为，当我们证明一个数学命题的时候，重要的是我们证明了这个命题在某个公理系统中可证这一元数学事实。一度作为ZFC形式主义②在典范翻译下也是一则集合论语句，即把自然数集定义为第一个无穷序数ω，再以标准的方式定义其上的运算。者的谢赫拉（Saharon Shelah）在已知ZFC关于正则基数为指数的幂所知甚少的情况下，提议尽可能在ZFC中证明关于奇异基数为指数的幂的取值上限，并证明了著名的不等式：2ℵω＜ℵω4。证明使用了谢赫拉发明的相比基数幂运算更精细的共尾可能性理论（pcf theory），涉及在各种超积模型中可能的共尾数。这依赖于相当深刻的集合直观。尽管所有在ZFC公理系统中的证明自然都会有相应的元定理作为副产品，但即使在ZFC形式主义者看来，他所证明的是一则关于集合的事实，而不是一则有穷的算术“元数学”命题。事实上，没有人真正给出过见证ZFC⊢2ℵω＜ℵω4的形式化证明的编码。

裘江杰在《集合论多宇宙观与形式主义》中认为形式主义能够帮助探究集合论新公理。后者是哥德尔纲领的核心议题，也被认为是柏拉图主义面对不完全性现象的标准回应。裘江杰写道：“为获得具有某种独立性的常规数学结果所必须的命题可能可以作为新公理的候选。这一进路是形式主义的。”[3]对这句话可以有两种解读。一种是，得到独立性结果这种“元数学”结果所必须的命题可以作为新公理的候选；第二种是，要证明已知独立命题（如独立于ZF的CH）所必须的命题可以作为新公理的候选。已知的独立性元数学结果（由一对相对一致性命题组成）往往是在弱如PRA这样的有穷主义公理系统中可证的，并不需要什么扩张了现有集合论公理系统的新公理候选。因此，第一种解读可以排除。关于第二种解读，来自形式主义对新公理的要求是证明目标已知独立命题所必须的命题。笔者认为，这是不合理的。按照哥德尔纲领对新公理的标准的讨论，集合论新公理除了必须满足符合我们关于集合概念的直观这一内在性要求，还应该具有成果丰富性这一外在性要求，即可以加深我们关于集合论宇宙的理解。除去丰富性要求，最“安全的”新公理无疑是将目标独立问题或其否定本身作为新公理，这恰好符合形式主义者的上述要求。目前关于集合论新公理的主要候选理论（W.Hugh Woodin的终极L、力迫公理和内模型假设）都有远超连续统假设问题的丰富后承。又或许形式主义者思考的对新公理的探究是类似反推数学的工作，后者试图厘清被广泛接受的数学成果所需要的最小二阶算术公理系统是什么。由此，构造主义者可以在选择他们所认可的公理系统之前就了解他们能够保留什么以及必须放弃什么。反推数学的一些工作的确被宣称为希尔伯特纲领的部分实现[13]。但笔者认为这类工作意义在于为部分怀疑论者在选择可接受的极小系统时提供参考，所涉及的都是在柏拉图主义者看来显然成立的公理系统。它与为集合论乃至全部数学寻找新公理的哥德尔纲领的志趣相去甚远。综上，形式主义思想对探究新公理的作用十分有限。

三、集合论多宇宙观与形式主义

笔者曾在《集合论多宇宙观述评》中论证集合论多宇宙观要么就是一种形式主义，要么与集合论单一宇宙观相容[2]。近年来，围绕集合论多宇宙观的研究出现了更多的结果。这让我们有理由再次审视集合论多宇宙观是如何推动有关数学实践的。本节中，笔者尝试通过展示这些基于集合论多宇宙观的新进成果以显示形式主义的思想何以在其中缺位，相反它们的灵感仍然主要来自多宇宙观与柏拉图主义单一宇宙观的对话。

近年来，与集合论多宇宙观密切相关的成果中最引人注目的是薄葉季路在2017年证明的下述定理。

定理

（1）假设V满足ZFC，那么V的地基是强向下直的（strongly downward directed）。即对任意索引集I和V的地基“集”{Ni}i∈I，存在V的地基N⊂i∈INi。

（2）假设集合论宇宙V中存在超巨基数（hyper-huge cardinal），那么V的地幔（mantle）就是V的地基（ground）[14]。

其中，我们称V的一个内模型M是V的地基，当且仅当V是M的一个集合力迫扩张，也即存在一个偏序P∈M以及一个(M,P)-泛型滤G 使得，V=M[G]。Richard Laver 和Woodin-Joel D.Hamkins 独立证明了V的地基可以被统一地在V中参数定义。V的地幔被定义为V的所有地基的交。由于地基们可以被统一的参数定义，地幔也是V的一个可定义的子类。但地幔是一个ZFC 内模型或进一步是V的地基并不是一个平凡的事实。

集合论地质学（set-theoretic geology）由Gunter Fuchs、Hamkins 和Jonas Reitz 提出[15]，目的是研究V的地基组成的结构，它可以被看作包含V的整个泛型复宇宙（generic multiverse）①认为集合论（甚至一般数学工作）就是在ZFC这个公理系统中做证明，科恩（Paul Cohen）是其代表。基于这个立场，他认为他关于连续统假设独立性的证明已经终结了连续统假设问题，即它和它的否定都不可证。的一段向下的锥形（downward cone）子结构，因而也是多宇宙观框架下研究的一部分。其中的一个重要的问题是V的地基们是否是向下直的（downward direct，即V的任何两个地基的交包含一个V的地基）或强向下直的。地基是向下直的对整个泛型复宇宙是很重要的性质。如果V的地基是向下直的，那么V地幔就是一个力迫不变的概念，即，V的任意集合力迫扩张V[G]的地基仍然是V的地基。例如，可构成集类L 和Woodin 设想的终极L 都是力迫不变的。并且V的地幔也是V的内模型（V中可定义，V中传递，与V等高的ZFC 模型）。事实上，V的地幔是V的最大的力迫不变的内模型。此外，V的地幔是V所在泛型复宇宙中任何一个宇宙的地幔，也是包含V的整个泛型复宇宙的交。由向下直性可以证明，泛型复宇宙中的任何两个宇宙N0，N1之间可以通过先取一次地基再做一次力迫扩张从而两步连接起来。

注意，我们仍然需要足够强的大基数假设，也即在上述薄葉季路的第二个定理下，才能得到V的地幔也是V的一个地基，从而属于包含V的泛型复宇宙。薄葉季路的第二个结论来自假设V中存在足够强的大基数κ，那么V的任何地基都是通过一个＜κ的力迫得到V的。因此，V的地幔可以通过一步集合力迫得到V。他将这里的大基数假设进一步削弱为存在一个可扩张基数（extendible cardinal）[16]。每个超巨基数是可扩张基数的极限，它本身也是可扩张基数。在整个大基数强度层谱中，可扩张基数相比超紧基数并没有强很多。Woodin 的终极L 计划来自他的下述发现：对V中的存在的任何已知的大基数κ（可能远强于超紧基数），如果N是V的一个超紧基数的弱张子模型（weak extender model），那么κ大基数性质相对于N是绝对的。因此，如果我们能找到一个包含超紧基数的具有精细结构的类似L 的弱张子模型（终极L），那么它也兼容任何V中存在的大基数。由此，假设V=终极L 在大基数层谱上不会损失任何解释力强度。注意，薄葉季路的结果表明，如果存在可扩张基数κ，那么κ以上的大基数在整个泛型复宇宙中（相对地幔）是绝对的（无法通过Lévy力迫坍塌κ及以上的基数）。地幔的这个性质与上述终极L的性质相呼应。加之，地幔本身是最大的力迫不变的（作为一种类似L 的性质，Woodin 要求终极L 也是力迫不变的）内模型，无怪乎Woodin 为这一结果欢呼并声称：“任何V=终极L 的公理候选都蕴含V就是泛型复宇宙的那个极小元②一般定义泛型复宇宙为一个集合论宇宙组成的类，它可以由其中任何一个集合论宇宙通过在取力迫扩张和地基下封闭得到。。”[17]需要注意的是，根据Fuchs 等人的证明[15]，任何一个ZFC 模型可以是某个ZFC 模型的地幔。所以假设V=V的地幔并不能直接带来多少有价值的推论，这与V=终极L 仍然相去甚远。

另一个值得注意的有关多宇宙观的进展来自Hamkins等人关于集合论潜在主义系统的模态逻辑刻画。Hamkins 和Benedikt Löwe 曾证明了ZFC 可证的力迫扩张关系的模态逻辑理论恰好是S4.2[18]。然而，Hamkins 主张的多宇宙观远不止由力迫法生成的泛型复宇宙。Hamkins 和Woodin 定义了一个普遍有穷集（universal finite set）{x:φ(x)}。φ是一个集合论Σ2公式，ZFC可证它定义的集合是有穷的[19]。而如果它在某个可数ZFC 模型M中定义了一个有穷集合y∈M，那么对任何有穷z∈M都存在M的一个顶扩张N使得{x∈N|φN(x) }=z。这里，我们称N是M的一个顶扩张（top-extension），当且仅当M是N的子模型，并且每个N∖M中的元素在N中冯诺依曼层谱上的秩（rank）都在M中的每个序数之上。利用普遍有穷集在诸顶扩张中可以被任意扩张，可以构造一系列“铁路开关”（railway switches）。即一系列集合论语句σ，使得◇□σ和◇□¬σ都成立，同时□σ和□¬σ都尚未成立。这里◇σ在某个集合论模型上成立，当且仅当存在它的一个满足σ的顶扩张。这些“铁路开关”的存在导致.2公式◇□σ→□◇σ无法成立。由此可以证明由可数集合论模型在顶扩张关系下生成的潜在系统（potentialism system，也是整个集合论复宇宙的一个子结构）的模态理论恰好是S4，也即任何一个潜在系统模态理论的下界。

薄葉季路的结果同时被作为单一宇宙观代表的Woodin 以及作为多宇宙观代表的Hamkins 喝彩。前者将其看作是一个非常强烈的信号，指示存在着典范的集合论宇宙，它同时具有力迫不变性和保持对大基数的解释力这两条良好的性质。后者将其视作对集合论复宇宙研究的一个典范成果，它大幅推进了我们对ZFC泛型复宇宙结构的理解，同时他又没有削减这个复宇宙的丰富性（任何ZFC模型都可以是地幔）。Hamkins 关于基于顶扩张的潜在系统模态性质的研究与他关于其他集合论复宇宙子结构的研究一样，意在展示复宇宙的丰富性与复杂性。为了维持实在论的立场同时摆脱传统单一宇宙观的统领，集合论多宇宙观的拥护者总试图通过展示复宇宙的丰富性来揭示人们关于“集合”的概念是不清晰的，甚至并不存在“真正的集合概念”。可见，有关集合论多宇宙观的研究仍然紧密围绕着这些经典的本体论问题。在其中，来自形式主义的启发、助探和事后的解释是缺位的。

四、结论

自哥德尔不完全性定理至今，形式主义作为一种在数学工作者共同体中被广泛接受的数学哲学立场，在严肃的数学基础与数学哲学的思考与讨论中始终处在边缘地位，除了受希尔伯特纲领启发而发展起来的证明论研究，这种往往被用来躲避哲学讨论的消极立场并没有为数学实践带来更多的启发，这一状况在有关数学基础的最新研究进展中也没有显著改善，形式主义的拥护者需要拿出更具体且具有吸引力的研究纲领才能使这种经典的数学哲学立场重获生机。

反观集合论多宇宙观自提出以来明显推动了集合论的有关研究，薄葉季路的工作不仅对集合论多宇宙观本身，而且对集合论和数学基础研究整体有着可观的推动作用。围绕集合论多宇宙观的这些结果诉说着多宇宙观这种基于集合论研究实践产生的新兴的数学哲学立场超出形式主义的价值。