刚度比对框架-核心筒体结构抗震性能的影响

阮左正

(沈阳铝镁设计研究院有限公司，辽宁 沈阳 110001)

0 引 言

框架核心筒中的外框架部分采用型钢砼柱和H型钢梁，内部筒体部分采用钢筋混凝土剪力墙结构。H型钢梁与内部筒体采用铰接连接，与型钢砼柱刚性连接。由于软件的局限性，壳单元不能设置塑性铰，因此对于筒体进入塑性阶段的性能需要考虑采用等效转化的方法，通常的做法是采用将剪力墙简化成框架斜支撑的宏模型，结构简化模型见图1。

图1 框架-筒体简化计算模型示意图Fig.1 Simplified calculation model of a frame-cylinder structure

1 框架与筒体刚度比对结构受力性能的影响分析

1.1 分析方案

按照上节介绍的简化方法将剪力墙等效成斜支撑结构，采用振型分布的形式，对该结构进行空间计算分析并得到前三阶振型模态分析结果。并采用如下2种方案进行对比分析。方案1：主要构件截面尺寸见表1。为了改变框架部分与筒体部分的刚度比，先保证筒体刚度不变即剪力墙厚度不变，通过调整框架柱截面尺寸来改变外部框架部分的刚度。

表1 方案1模型主要参数Tab.1 Main model parameters for scheme 1

方案2：主要构件截面尺寸见表2。保证外部框架刚度不变即框架柱截面尺寸不变，通过调整核心筒体的剪力墙厚度改变筒体部分的刚度。

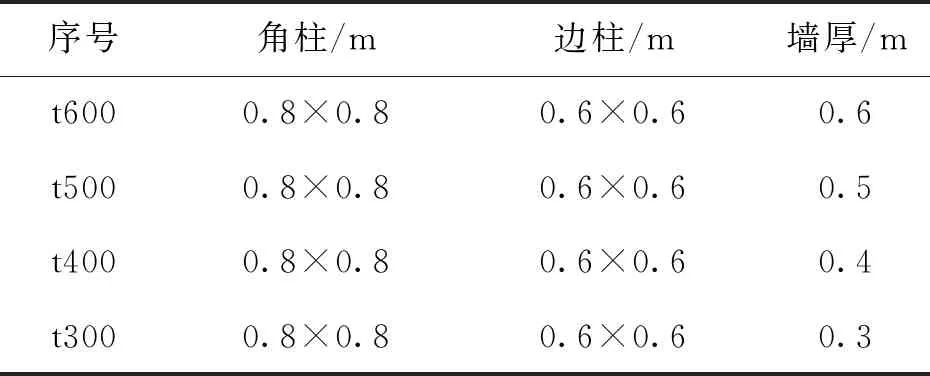
表2 方案2模型主要参数Tab.2 Main model parameters for scheme 2

1.2 计算结果分析

1.2.1 楼层剪力

为分析刚度比对各层剪力值分配情况的影响，对上述分析模型进行push-over分析，能够得出各个楼层剪力值在多遇地震和罕遇地震的变化情况。

(1)方案1楼层剪力

不同框架柱截面尺寸下的各楼层剪力占总基底剪力的百分比见图2，图中即包含多遇地震也给出了罕遇地震情况下百分比。图中Ⅰ～Ⅳ代表表2中的4种不同模型。

通过对图2的分析，可以得出如下结论：各楼层剪力值得变化趋势变化不大，并不受多遇地震或者罕遇地震的影响。①当筒体剪力墙厚度不变，即核心筒刚度相同的条件下，框架部分所承担剪力随柱截面尺寸的加大而增加，相应的筒体所承担剪力减小。②层数越高，框架部分所承担剪力的百分比越大，当筒体剪力墙进入屈服阶段后，框架剪力百分比变大的趋势更加明显，而底层框架所承担剪力百分比是最小。

图2 方案1各模型剪力分配Fig.2 Shear force distributions in models for scheme 1

(2)方案2模型楼层剪力

不同筒体剪力墙厚度下的各楼层剪力占总基底剪力的百分比见图3，图中即包含多遇地震也给出了罕遇地震情况下百分比。

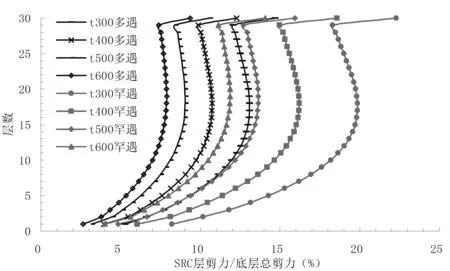
图3 方案2各模型剪力分配Fig.3 Shear force distributions in models for scheme 2

通过对图3的分析，可以得出如下结论：①罕遇地震情况下，随着筒体剪力墙厚度的变大，20层以下的框架所承担的剪力所占百分比相对较小，而20层以上，各楼层框架承担剪力所占百分比趋于相同。从而可得出，框架部分承担剪力所占百分比受筒体剪力墙厚度影响很小。②多遇地震情况下，结构仍然在弹性范围内，框架承担剪力占比沿层高分布趋势与理论模型基本一致，即最下部趋于零，向上逐渐增加，大概在20层附近达到极值，之后减小，然后在顶层会有明显加大。筒体剪力墙厚度的变化对剪力占比影响不大。

1.2.2 楼层倾覆力矩

(1)方案1楼层弯矩

对于高层结构，在计算分析过程中，倾覆力矩必须作为一项重要指标得到检验。图4、图5示意出了方案1中不同模型的外部框架和内部筒体弯矩以及总弯矩沿楼层高度的变化情况，既包含多遇地震也包含罕遇地震下的情况。

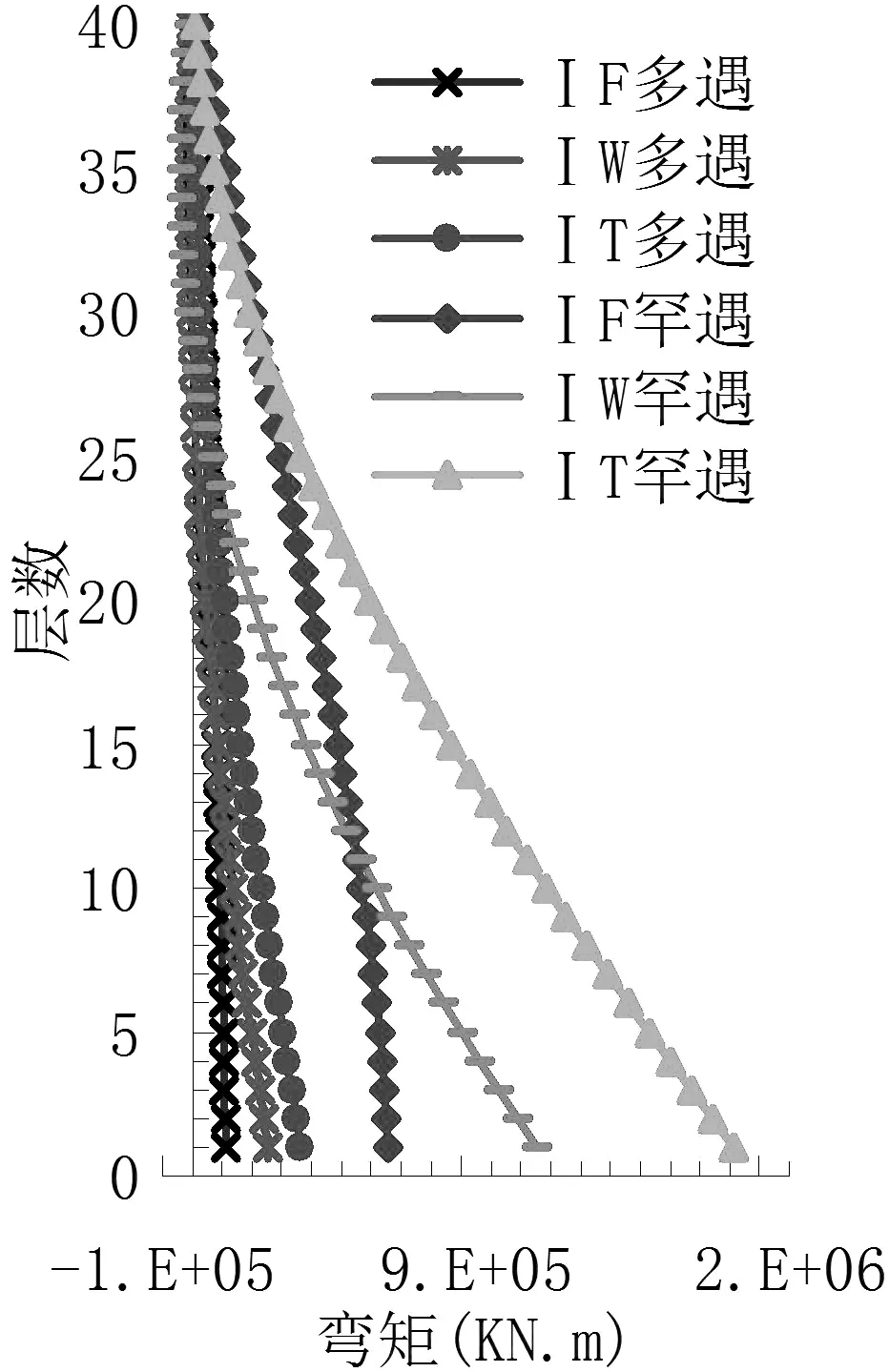
(a)模型Ⅰ

图5 方案1各模型各楼层弯矩所占百分比Fig.5 Bending moment shares in stories of each model for scheme 1

(2)方案2楼层弯矩

不同筒体剪力墙厚度下，框架和筒体部分各楼层弯矩以及弯矩沿楼层所占百分比的变化情况见图6、图7。

(a)模型t300层弯矩

图7 方案2各模型各楼层弯矩所占百分比Fig.7 Bending moment shares in stories of each model for scheme 2

通过图6、图7的分析可知：框架部分和筒体部分所承担的弯矩及所占总弯矩百分比分别随着框架柱截面和筒壁剪力墙厚度的增大而增加，这一趋势并不随着多遇地震和罕遇地震而变化。从图中可以看出，10层以下，弯矩值和所占百分比的变化趋势更加明显，而10层以上变化趋势减弱，即高层结构的底部弯矩值对构件截面尺寸的变化更加敏感。

1.2.3 结构侧向变形

(1)方案1模型位移分析

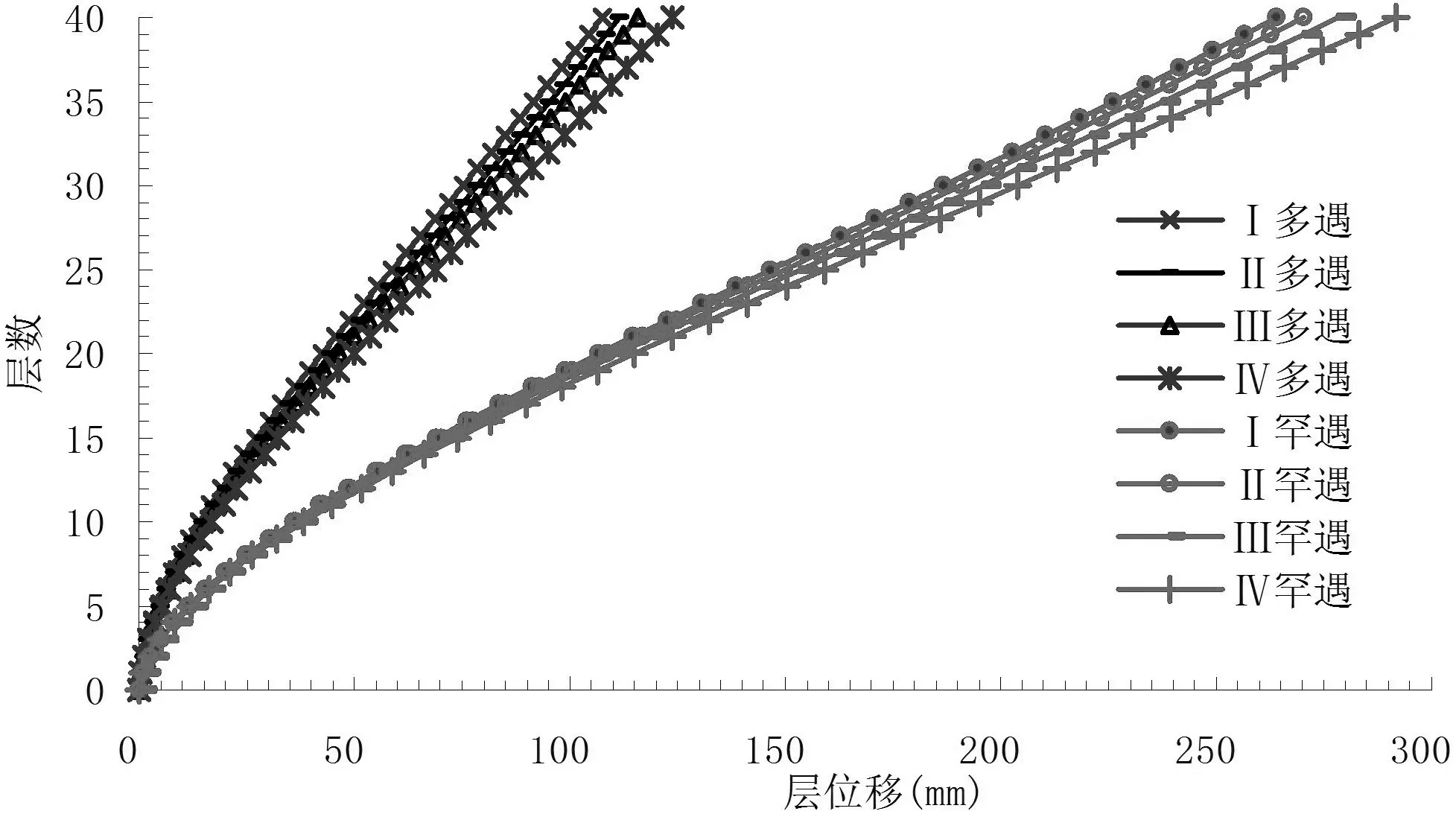
多遇地震和罕遇地震情况下，框架柱截面尺寸的变化对层位移和层间位移角的变化趋势见图8。

(a)层位移

通过图8的分析可知：①层位移、层间位移角随着框架柱截面尺寸的增大而减小。而且层间位移和位移角在20层以上的变化很小，在20层附近最大；②表3给出了多遇地震和罕遇地震情况下的最大层间位移角，同时给出了相应的楼层位置；③层间位移随着层数变化呈弯曲型；④多遇地震条件下，随着框架柱截面尺寸的减小，层间位移角最大值所在楼层位置明显上移，而罕遇地震则趋势相反。

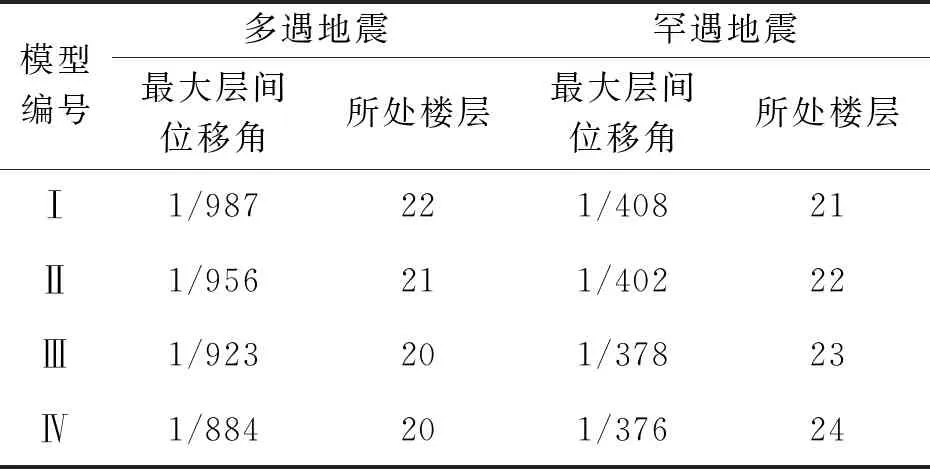
表3 最大层间位移角及其位置Tab.3 Stories and the maximum inter displacement angles

(1)方案2模型位移分析

筒体刚度变化的4种模型在多遇地震和罕遇地震作用下的位移值见图9。

通过对图9的分析可知：①层位移、层间位移角随着筒体剪力墙厚度的增大而减小。而且层间位移和位移角在15层以上的变化幅度很小，在15层附近最大；②表4给出了多遇地震和罕遇地震情况下的最大层间位移角，同时给出了相应的楼层位置；③层间位移随着层数变化亦呈弯曲型；④多遇地震条件下，随着筒体剪力墙厚度的增加，层间位移角最大值所在楼层位置明显上移，而罕遇地震则趋势相反。

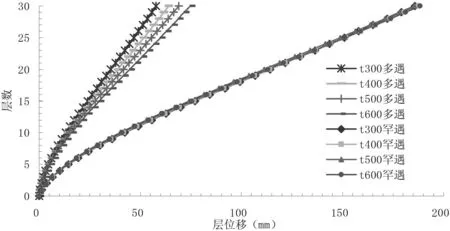
(a)层位移

表4 最大层间位移角及其发生的位置Tab.4 Stories and the maximum inter displacement angles

2 结 语

通过改变外部框架与内部核心筒间的相对刚度，对比分析了刚度比对抗震性能的影响，经计算和对比分析得出以下结论：

(1)对于钢筋砼-核心筒这种结构，框架部分所承担剪力占总剪力的百分比随着框架与筒体刚度比的增大而增加，尤其在弹塑性阶段，所占百分比加大的更加明显；

(2)框架所承担的楼层弯矩占总弯矩的百分比随着刚度比的增加而加大，但增加的并不明显；

(3)无论是多遇地震还是罕遇地震，框架核心筒结构的整体变形趋势都是弯曲型，而这种趋势受刚度比的影响并不大；

(4)外部框架与内部筒体的刚度比对结构侧向变形和层间位移角的影响很小，随刚度比的增加，结构变形稍有增大。