牙轮钻头牙齿镶装工艺有限元研究*

吴泽兵 周珂飞 陈汉杰

(1.西安石油大学机械工程学院 2.中国石油新疆油田公司工程技术公司)

0 引 言

牙轮钻头是石油钻井工程中有效的破岩工具之一，主要以变角度的压入加刮凿方式破碎岩石，其牙齿在破岩过程中做三维复合运动[1-2]。由于钻头工作环境复杂，工作时承受钻压、弯矩和剪切力等载荷作用，牙齿失效现象[3-5]时有发生。长期以来，众多学者针对牙轮钻头做了大量研究，从研究内容来看，主要是钻头设计以及压齿力和固齿力计算[6-8]等。陈涵宇[9]通过分析传统的布齿结构，提出了新型倒锥齿结构，可以有效地增大牙齿的固紧力，减少脱齿现象的发生；邓嵘等[10]采用拉宾诺维奇磨粒磨损模型，建立了牙齿与岩石互作用模型，探索了转速、机械钻速与牙齿磨损之间的关系；谢苗等[11]从牙轮钻机钻井时钻头纵向振动特性对牙轮轴端的影响进行牙轮轴端磨损机理分析，所得结论对延长牙轮钻头寿命具有一定的积极作用。但总体来说，对钻头牙齿失效的研究较少，特别是有关镶齿牙轮钻头牙齿镶装工艺方面的研究更少。

在实际钻井中，钻机施加足够大的轴压作用在牙轮钻头上，将镶嵌在牙轮上的合金齿嵌入岩土表层，同时主机钻杆带动牙轮钻头做旋转运动进行破岩，载荷主要通过牙齿传入岩石，容易出现牙齿脱落和磨损等[12-13]现象，造成部分钻头因牙齿失效而报废，牙齿脱落成为钻头失效的一种重要形式。研究表明，牙齿与齿孔主要通过过盈配合[14-15]来连接，钻头牙齿脱落主要是牙轮对牙齿缺乏足够的固齿力。为了降低钻井成本，提高钻井效率，减少钻头失效[16-18]，目前针对钻头牙齿失效问题，主要从设计、加工、装配工艺和使用等方面进行改进。

本文利用有限元分析软件ABAQUS研究不同镶装工艺对镶齿牙轮钻头固齿力、Mises应力和变形的影响[19-23]，通过模拟不同镶齿工艺得到固齿力和压齿力等参数，总结了不同镶装工艺对镶齿牙轮钻头的影响，进而确定了最佳镶装工艺。所得结论对镶齿牙轮钻头的实际生产加工具有一定的参考意义。

1 牙轮钻头镶齿数值模拟方法

1.1 有限元模型

本文基于有限元分析软件ABAQUS模拟计算不同镶装工艺所产生的应力-应变场。由于ABAQUS软件实体建模的局限性，首先在Creo软件中建立三维几何模型，然后以x_t格式导入ABAQUS中进行分析计算。ø215.9 mm(8in)牙轮钻头全齿模型如图1a所示。在有限元模拟时考虑计算速度与精度，简化模型，并利用ABAQUS软件进行几何模型的网格划分，结果如图1b所示。该牙轮钻头包括3个齿圈加1圈保径齿共4圈齿。各齿圈参数如表1所示。由圣维南原理可知，模型简化后对分析精度的影响非常小，分析结果在精度要求范围内，同时为了方便载荷施加，简化了牙齿齿端结构。

图1 牙轮钻头牙轮模型及网格划分图

表1 牙轮钻头各齿圈参数

由于模型较为复杂且不是一个完整的回转体，采用四面体网格划分方式，划分完成后共有37 933个节点，166 252个网格单元，网格类型为C3D4。针对牙齿压入齿孔的镶装过程，研究的是牙齿运动到不同位置的静态响应，因此分析步类型为Static General，牙齿与齿孔接触面摩擦因数为0.1，并选取牙齿表面为主接触面，齿孔面为从接触面，镶齿前根据牙齿数量建立相应的局部坐标系。镶齿时对牙齿齿顶面施加位移载荷，完全约束牙轮内表面。

1.2 材料参数

根据牙轮钻头工作情况和受力特点，牙轮壳体材料选择具有高淬透性、高强度及表面硬化加工法的渗碳钢20Ni4Mo，强度极限1 423 MPa。以前部分镶齿牙轮钻头研究中为了简化分析，将牙齿视为刚体，本文依据实际情况，牙齿采用高强度、高冲击韧度及弹塑性较好的钨钴类硬质合金YG06A，抗弯强度3 200 MPa。牙齿与齿孔材料力学性能参数如表2所示[24]。

表2 牙齿与齿孔材料性能参数

1.3 镶装工艺确定

目前镶齿牙轮钻头全齿镶装没有明确的装配方案，在逐个镶齿时随意性较大，本文对ø215.9 mm牙轮钻头镶齿顺序进行研究，研究3个齿圈与保径齿圈共4个齿圈的镶装顺序对牙轮壳体的影响。由于牙齿材料为硬质合金，相较于牙轮壳体刚度较大，所以着重研究镶装顺序对牙轮壳体变形和固齿力的影响。针对4个齿圈，考虑所有可能的镶装顺序，本文共设计了4种方案共24组镶装试验，具体试验方案如图2与表3所示。图2为牙轮钻头齿圈序号图，表3为24种镶装顺序，其中第1个数字为试验编号。

图2 齿圈序号

表3 镶齿方案

2 镶装结构理论及有限元模型验证

过盈配合时，当牙齿与齿孔过盈量增大到一定值时齿孔势必出现塑性变形，用塑性力学理论求解塑性变形的解析解很困难。本文运用的ABAQUS有限元分析方法是否准确需要验证，虽然在塑性变形阶段很难验证，但是在牙轮材料弹性范围内求解其弹性理论解，用弹性理论解对有限元分析方法进行验证却具有一定的可行性[9]。

2.1 理论分析

为了便于分析，本文将牙轮与牙齿的装配体简化为厚壁圆筒与实心圆柱模型，如图3所示，对此单齿孔模型用弹性力学进行解析。

图3 圆筒与实心圆柱理论模型

2.1.1 孔的受力分析

将厚壁圆筒的内压设为p1，外压设为p2，内外压共同作用下周向应力设为σθ，径向应力设为σr，径向位移设为u。根据拉梅公式，有：

(1)

(2)

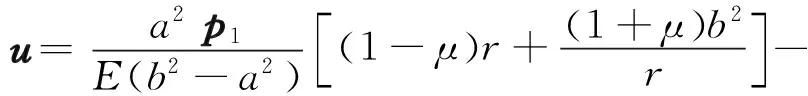
(3)

式中：E为弹性模量，GPa；μ为泊松比。

该单齿孔模型不考虑相邻齿孔的应力交互影响，孔壁仅受内压作用，根据圣维南原理，外压p2=0，外径b→∞，于是有：

(4)

(5)

(6)

式中：μk为牙轮材料的泊松比，Ek为牙轮材料的弹性模量。

2.1.2 齿的受力分析

将牙齿简化为实心圆柱，牙齿与齿孔接触面只受到均布载荷作用，p1=0，内径a→0，径向位移可用下式表示：

(7)

式中：μc为牙齿材料的泊松比，Ec为牙齿材料的弹性模量。

2.1.3 牙齿与齿孔过盈配合分析

由于牙齿与齿孔过盈配合，实际齿孔半径会比牙齿半径小，这样在过盈配合后牙齿和齿孔之间会产生径向压力p。设过盈量为δ，则完成装配后牙齿外壁半径的减小量与齿孔壁半径的增加量之和必须为δ，由式(6)和式(7)得：

(8)

整理后可得：

(9)

最终得到牙齿与齿壁的径向压力p为固齿力，即牙齿表面与齿孔表面法向接触力。

轴向应力σz与周向应力、径向应力相比很小，近似为0，这3个应力均为主应力，依据屈服准则下的Mises应力求解公式有：

(10)

2.2 模型验证

对于本文所使用的镶装方法的可靠性，采用理论计算与模型仿真进行对比，验证所用的理论计算模型如图4a所示。为了在弹性范围内求其理论解，该理论计算模型齿孔过盈量为0.02 mm，镶齿完成后Mises应力云图如图4b所示，其峰值为561.1 MPa。

图4 有限元模型及部分结果图

由式(9)可以计算出过盈量为0.02 mm时径向应力为190.1 MPa，由式(10)计算得Mises应力为337.8 MPa，理论计算得到的是齿孔壁所受应力平均值，对ABAQUS计算的固齿力和Mises应力分别求平均值，选取沿齿孔壁深度方向任意一条路径，沿路径求固齿力与Mises应力的平均值。ABAQUS计算的固齿力和Mises应力与理论解的对比如表4所示。

由表4可知，固齿力和Mises应力的误差分别为11.31%和7.22%，在工程允许误差范围内。这表明本文所采用的有限元方法正确，保证了数值计算的准确性和可靠性。

表4 固齿力和Mises应力与理论解的对比

3 仿真结果分析

第1组镶装完成后其Mises应力与固齿力云图如图5所示。由图5c可知，镶装完成后最大应力出现在牙齿上，牙齿材料相较于齿孔材料坚硬、密度高，因此主要研究牙轮壳体Mises应力。由图5b可知，牙轮壳体最大应力为685.0 MPa，未超过牙轮材料屈服强度。

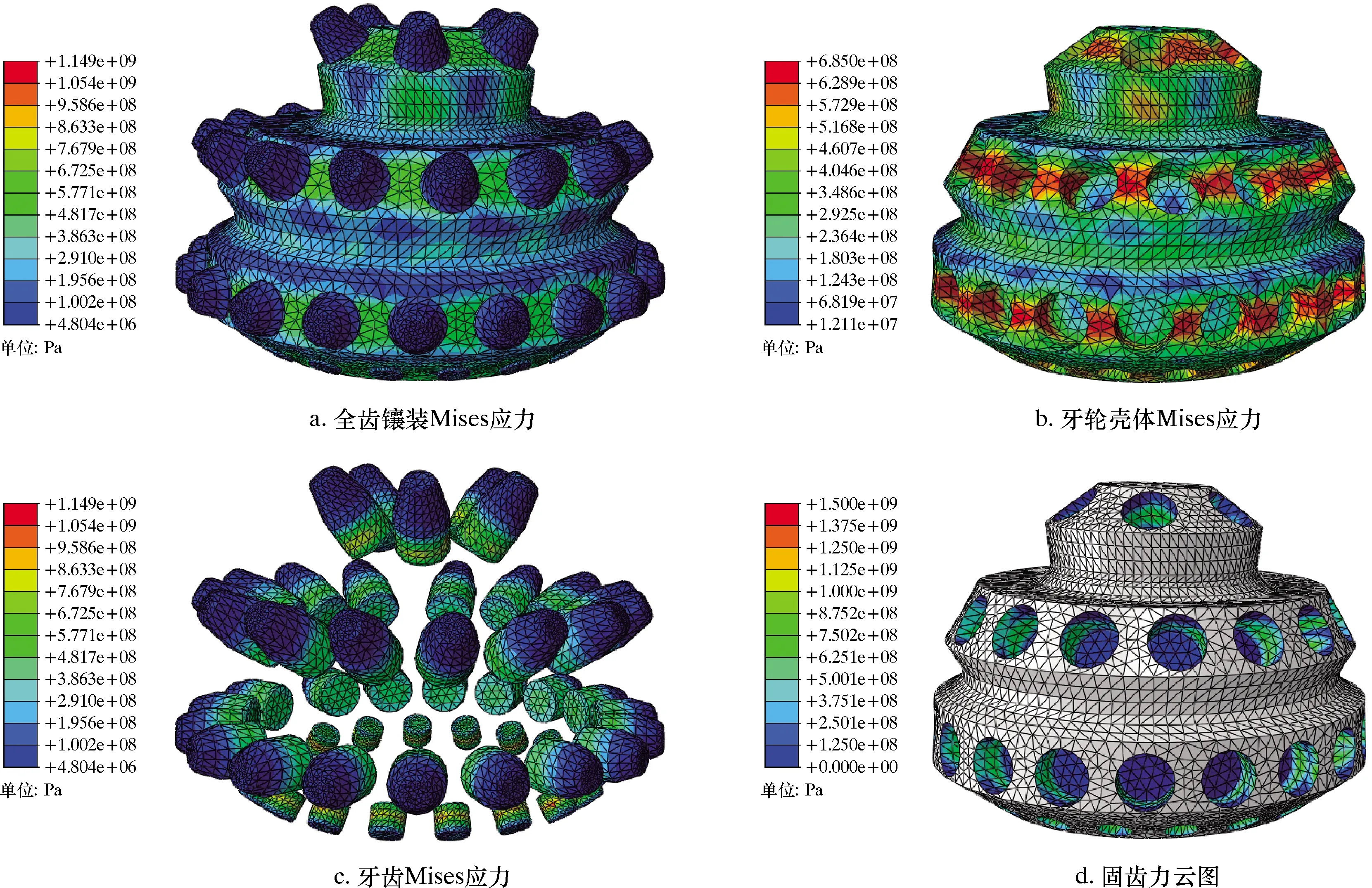
图5 Mises应力与固齿力云图

为寻求最佳镶装方案，即应力与变形均较小的镶装工艺，将应力与变形放置于同一图中研究。图6为24组试验牙轮壳体应力与变形折线图。由图6可知，牙轮壳体Mises应力处于屈服强度以下，且不同镶装顺序的应力变化不明显，结合不同工艺的变形量，最佳镶装工艺为9-3241和10-3214。由于试验较多，所以着重研究方案a中4组镶装顺序对Mises应力、固齿力和压齿力的影响。

图6 不同镶装方案时Mises应力与变形折线图

图7a是24种镶装工艺中Mises应力平均值折线图。由图7a可知，在初始时，牙轮壳体Mises应力较小，随着镶齿的进行，Mises应力有增大的趋势，最后镶齿的齿圈Mises应力最大。这是因为牙齿镶装过程属于过盈配合操作，牙齿在压入后齿孔产生变形，这种变形会随着镶齿的进行而累积，越靠后影响越大，导致后面镶齿的齿孔与牙齿过盈配合量增大，所以应力随着镶齿的进行有增大的趋势，最后镶齿的齿圈其齿孔Mises应力最大达683 MPa，但未超过牙轮材料的屈服强度。

图7b是方案a中第3、第4、第5和第6等4组试验Mises应力柱状图。由图7b可知，不同镶装顺序齿圈应力变化趋势相似，第2、第3齿圈Mises应力最大，第4齿圈应力最小。

图7 Mises应力的折线图和柱状图

图8a是24种镶装工艺中固齿力峰值折线图。由图8a可知，随着牙轮钻头牙齿的镶装，固齿力峰值有增大的趋势，最后镶装齿圈其固齿力峰值达到1 527 MPa，超过牙轮材料屈服强度1 035 MPa，但未超过牙齿材料抗压强度极限(2 157 MPa)。图8b是第3、第4、第5和第6组试验中固齿力均值折线图。

由图8b可知，不同镶装工艺固齿力变化趋势一致，其中第④齿圈固齿力最大。这是由于第④齿圈齿径最小，固齿力即牙齿表面与齿孔面的法向接触力，也称径向压力，由式(9)可知其与齿径成反比，所以第④齿圈固齿力最大。

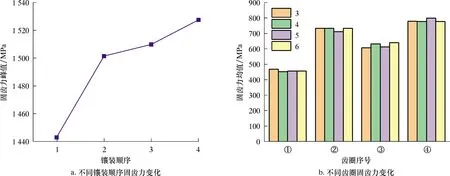
图8 固齿力的折线图和柱状图

图9a是24种镶装工艺中所得压齿力折线图。由图9a可知，随着镶齿的进行，牙齿压入齿孔所需压齿力快速增大，随后小幅减小，总体来说压齿力是增大的，即越靠后镶装的齿圈，压力机将牙齿完全压入齿孔所需最小压齿力增大。在实际镶装中，多轴自动镶齿设备针对不同齿圈镶装需要实时调整压力，以便牙轮钻头镶齿的顺利进行。图9b是方案a中第3、第4、第5和第6组试验压齿力柱状图。由图9b可知，不同镶装工艺下同一齿圈所需压齿力大小基本相同，第④齿圈所需压齿力最小，即将牙齿压入齿孔过程中需要克服的摩擦力较小，同一表面粗糙度下，该摩擦力与接触面积成正比，第④齿圈齿径小且齿身长度短，与齿孔有效接触面积小，因此将其压入齿孔需克服的摩擦力小。

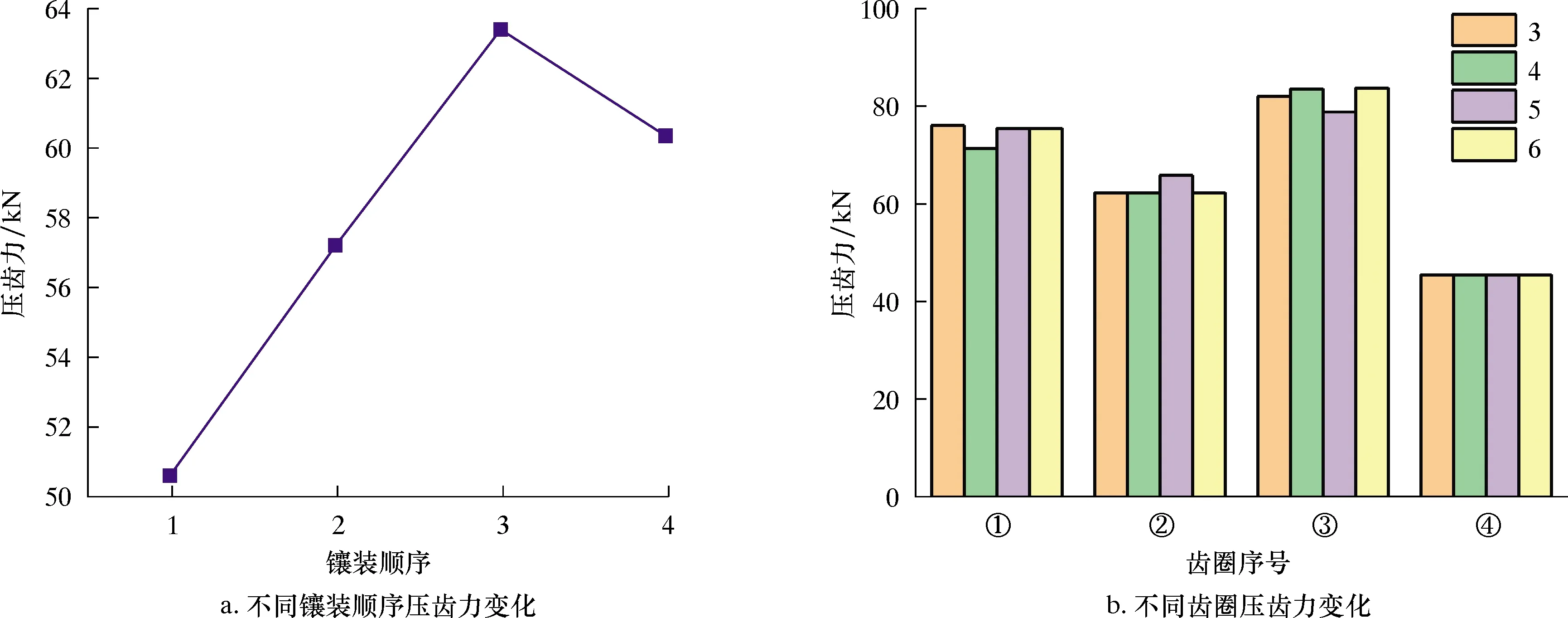
图9 压齿力的折线图和柱状图

由于试验方案设置较多，取一组来研究其壳体变形规律。图10是第1组镶装顺序牙轮壳体变形图。镶齿顺序为4321，监测点为最后一个齿孔圆周上某节点。

由图10a可知，随着镶齿进行，最后镶装的齿孔变形随之增大，越靠近最后影响越大。图10b是前51个齿镶装时齿孔变形图。由图10b可知，越接近最后齿圈，对齿孔变形影响越大，图中共3个波峰，即前3个齿圈镶齿时对最后镶装齿孔变形影响呈波浪趋势，以第④齿圈为例，共有18个牙齿，第1个波峰为前18个齿镶装时对齿孔变形的影响趋势，齿孔变形先增大，镶装过半时齿孔变形减小，这是因为在圆周方向基本均匀布齿，镶齿过半时对齿孔变形方向影响与之前相反。

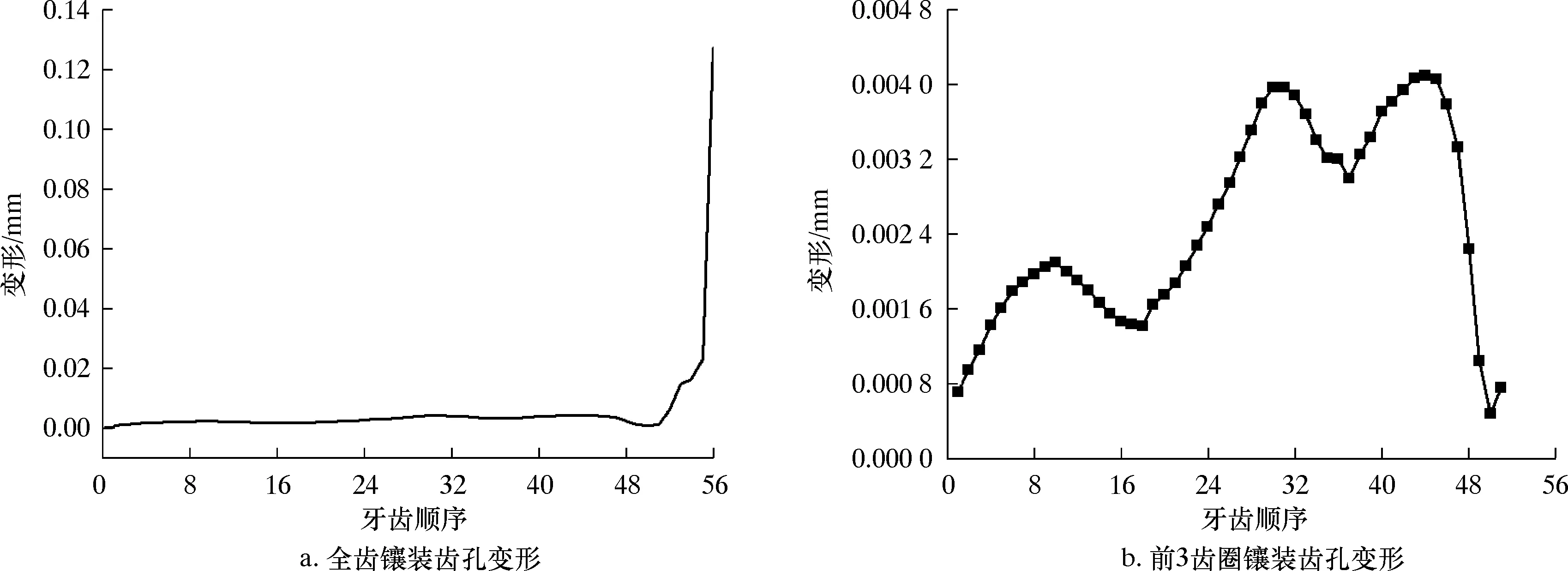
图10 牙轮壳体变形图

4 结 论

(1)有限元软件ABAQUS可以模拟计算牙轮钻头全齿镶装过程，且通过理论计算与仿真结果对比，误差在工程允许范围内，验证了建模方法以及有限元分析方法的可靠性与准确性，为实际镶装工艺制定提供了参考。

(2)针对ø215.8 mm牙轮钻头的24组镶装顺序，以壳体变形为评价准则，优选9-3241和10-3214为最佳镶装方案；同一镶装工艺下，先镶装的齿圈影响后镶装的齿孔变形，且以一个齿圈为周期，影响趋势呈波浪变化。

(3)不同镶装工艺下，越靠后镶装所需压齿力越大，即针对多轴自动压齿设备，其压力值设置可逐步增大，为压齿设备压力设置提供了一定参考；由于齿孔过盈配合，牙齿镶装后有变形累积，后面未镶齿齿孔受前面镶齿过程的影响产生变形，即不同镶装工艺下，越靠后齿圈镶齿其固齿力和Mises应力有增大的趋势。

(4)不同镶装工艺下，4个齿圈的Mises应力、固齿力和压齿力分别具有相同的变化趋势，且第④齿圈(保径齿)固齿力最大，Mises应力和所需压齿力最小。