水平井钻柱-井壁摩擦诱导黏滑振动机理研究*

朱杰然 邹德永 李光泉 杨宁宁 杨全进 林 伟

(1.中国石油大学(华东) 2.中石化胜利石油工程有限公司随钻测控技术中心3.中石化石油工程技术服务公司 4.西南石油大学工程学院)

0 引 言

钻柱系统的振动抑制是井眼轨迹优化、提速增效、钻井参数优化和智能钻井的重要基础[1]。为了抑制钻柱系统的黏滑振动，国内外学者开展了大量研究，并提出了很多黏滑振动抑制方法，包括主动控制策略和被动控制策略。冯程宝等[2]建立了多自由度集中质量扭转摆模型，单独考虑每根钻杆及底部钻具组合，将钻柱系统视为分段光滑的连续系统，研究了钻压、电机输出扭矩和转盘转速等钻井参数对钻柱黏滑振动的影响，并提出了控制黏滑振动的方法。随后，E.M.NAVARRO-LPEZ[3]对该多自由度模型进行简化，考虑钻杆与钻铤的运动行为，先后建立了转盘-钻柱-底部钻具组合-钻头四自由度和转盘-钻柱-底部钻具组合+钻头三自由度钻柱系统分段光滑模型。

2014年，M.SILVEIRA等[4]基于梁理论模型研究了非线性扭转刚度下弹性梁的扭转振动规律，并分析了变刚度系数下扭转运动的稳定域以及动力学分岔情况。M.SARKER等[5-6]应用三维多体动力学键合图建模方法，建立了水平段的轴向-扭转和横向-扭转动力学模型，研究了耦合作用下水平井钻柱系统动力学响应，并使用轴向冲击器减弱了钻柱系统的振动。LIN T.J.和HAN Y.W.等[7-8]通过建立钻柱系统的有限元模型，分析了钻柱的轴向、横向和扭转振动规律。HAN Y.W.等[8]还研究了钻压和转速对钻柱动力学的影响，发现当钻柱未发生屈曲时，钻柱系统响应较稳定，而当钻柱发生屈曲后，钻柱的运动发生紊乱，振动非常剧烈。

前人主要针对钻头的黏滑振动进行了研究，而忽略了钻柱与井壁的非线性摩擦也可能对黏滑振动产生一定的影响。也有学者通过建立简单的理论模型对钻柱诱导黏滑振动情况进行了分析。U.J.F.AARSNES等[9]假设钻柱与井壁摩擦为四参数的Karrnop非线性摩擦模型，通过分析定向井在钻头提离井底工况下钻头的黏滑振动特性，发现钻头仍然产生了黏滑振动。ZHAO D.P.等[10]将钻柱与井壁间的摩擦假设为Stribeck摩擦模型，通过对轴向运动分析，发现钻柱与井壁摩擦会导致钻柱轴向的黏滑振动现象。针对钻柱与井壁摩擦诱导黏滑振动，前人大多只从现场试验观察到了黏滑振动现象，而缺乏对钻柱-井壁摩擦诱导黏滑振动机理的研究。因此，本文基于非线性摩擦模型来进一步揭示该现象产生的机理，以期为油田现场施工提供理论指导。

1 水平井钻柱系统动力学模型

为了研究钻柱-井壁非线性摩擦对钻柱系统黏滑振动的影响，建立了离散的水平井钻柱系统动力学模型，如图1所示。整体模型为钻柱系统集中质量扭摆模型，然后基于该接触模型来进行全井钻柱的系统动力学计算。

图1 水平井钻柱系统动力学模型

在集中质量扭摆模型的基础上引入了钻柱与井壁间的非线性摩擦因素，来研究井壁摩擦对钻柱扭转振动的影响。钻柱与井壁间摩擦采用光滑的Stribeck摩擦模型。

将直井段、造斜段和水平段分别等效为不同数量的集中质量单元，各单元因钻柱与井壁间的接触而产生摩擦扭矩。在仿真过程中为了提高计算效率，对模型进行了适当简化：①将顶驱/转盘、垂直段管柱、造斜段管柱和钻头都等效为一个扭转刚度单元，水平段等效为n个集中质量单元；②忽略钻柱接头和钻井液对钻柱受力的影响；③不考虑井筒变径问题；④忽略轴向、横向耦合振动而引起的井壁接触力变化，即接触力保持恒定。

根据Hamilton原理，系统的动力学微分方程可以表示为：

(1)

T可表示为：

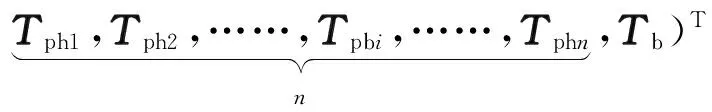
(2)

其中Tpv、Tpbu、Tphi可以表示为：

Tpv=0

(3)

Tpbu=μpbuFNro

(4)

Tphi=μphiqLiro

(5)

式中：Tpv为垂直段管柱与井壁的摩擦扭矩，由于垂直段无接触，所以摩擦扭矩为0；Tpbu为造斜段管柱与井壁的摩擦扭矩，N·m；FN为管柱与井壁接触力，N；Tphi为水平段管柱与井壁的摩擦扭矩，N·m；q为管柱单位长度重力，N/m；Li为管柱长度，m；ro为管柱半径，m。

U为转盘提供的驱动扭矩，可表示为：

U=(u,0,……,0)T

(6)

假设钻柱与井壁之间的摩擦符合光滑的Stribeck摩擦模型，则管柱与井壁之间的动态摩擦因数可表示为：

(7)

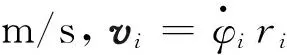
为了解钻柱系统与井壁摩擦对黏滑振动的影响，黏滑振动系统的钻头-岩石互作用可以忽略，即分析钻头提离井底时钻柱系统的受力及动力学响应，因此对垂直井段、造斜井段以及水平井段的受力进行了分析。

垂直段管柱不与井壁接触，故无摩擦扭矩。假设水平段管柱轴向力为0，则造斜段管柱从造斜点开始到水平段入口处，其法向接触力可表示为：

(8)

轴向力的变化量可表示为：

ΔF=qcos(α-Δα/2)-μFN

(9)

式中：ΔF为管柱轴向力随井深的变化量，N；α、β分别为井斜角和方位角，(°)。

为了对模型进行简化，假设造斜段无闭合方位角变化，即β=0，则法向接触力的表达式可写成：

FN=FtΔα+qsin(α-Δα/2)

(10)

将式(10)带入式(9)，则可得轴力的变化表达式：

ΔF=qcos(α-Δα/2)-

μ[FtΔα+qsin(α-Δα/2)]

(11)

由于水平段入口处轴力为0，对ΔF进行积分：

(12)

求解该式可得造斜点处的轴向力：

(13)

式中：r为造斜段半径，m。

(14)

假设水平段管柱既不受拉也不受压，则管柱与井壁之间的接触力只与单位长度管柱的重力有关，即有：

FNh=qLi

(15)

本文对一口三段制小井眼水平井进行了仿真分析，该井垂直段长度为3 000 m，水平段长度为1 500 m，每30 m井段造斜率为6°。直井段管柱直径为127.0 mm，造斜段和水平段管柱直径为88.9 mm。将水平管柱按每100 m简化为一个集中质量单元，共简化成15个集中质量单元，造斜段和垂直段分别简化成一个质量单元，钻头简化成一个质量单元，其中造斜段管柱与井壁间的动、静摩擦因数分别为0.3和0.5，水平段管柱与井壁间的动、静摩擦数分别为0.4和0.6，钻井液密度为1.1×103kg/m3，钻杆密度为7.85×103kg/m3。

2 钻头提离井底动力学响应分析

对钻头提离井底时的钻柱系统动力学响应进行分析，此时无钻压作用在钻头上。将水平段管柱离散成15个质量单元，第1个质量单元距离井口最近，每个质量单元模拟长100 m的水平管柱。垂直段和造斜段分别用一个集中质量单元进行模拟。

首先分析了转盘转速为2π rad/s时钻柱系统的动力学响应。图2为直井段管柱和造斜段管柱转速随时间的变化曲线。从图2可以看出：直井段管柱在启动阶段转速波动上升，在达到最大转速后存在小幅下降，最后保持匀速转动；而造斜段管柱由于受到井筒与管柱间的摩擦扭矩作用，在启动阶段速度波动量就较大，甚至达到了黏滑振动，但随着速度的进一步增加，造斜段管柱转速振荡衰减，最后也和直井段管柱一样保持相同恒定转速运行。

图2 直井段及造斜段管柱转速随时间的变化曲线(转盘转速为2π rad/s)

图3为钻柱系统水平段管柱转速随时间的响应特性曲线。图3中n=1、4、8、12和15，分别表示距井口不同距离的离散质量单元，n=1的质量单元距离井口最近，而n=15的质量单元距离井口最远。在起始阶段管柱都发生了一个小幅的波动，且距离井口越近，管柱的转速波动越剧烈。在转速波动之后，水平段管柱转速都发生振荡衰减，最后都保持匀速转动。从图3可以明显看出，距离井口越远，管柱波动越小。

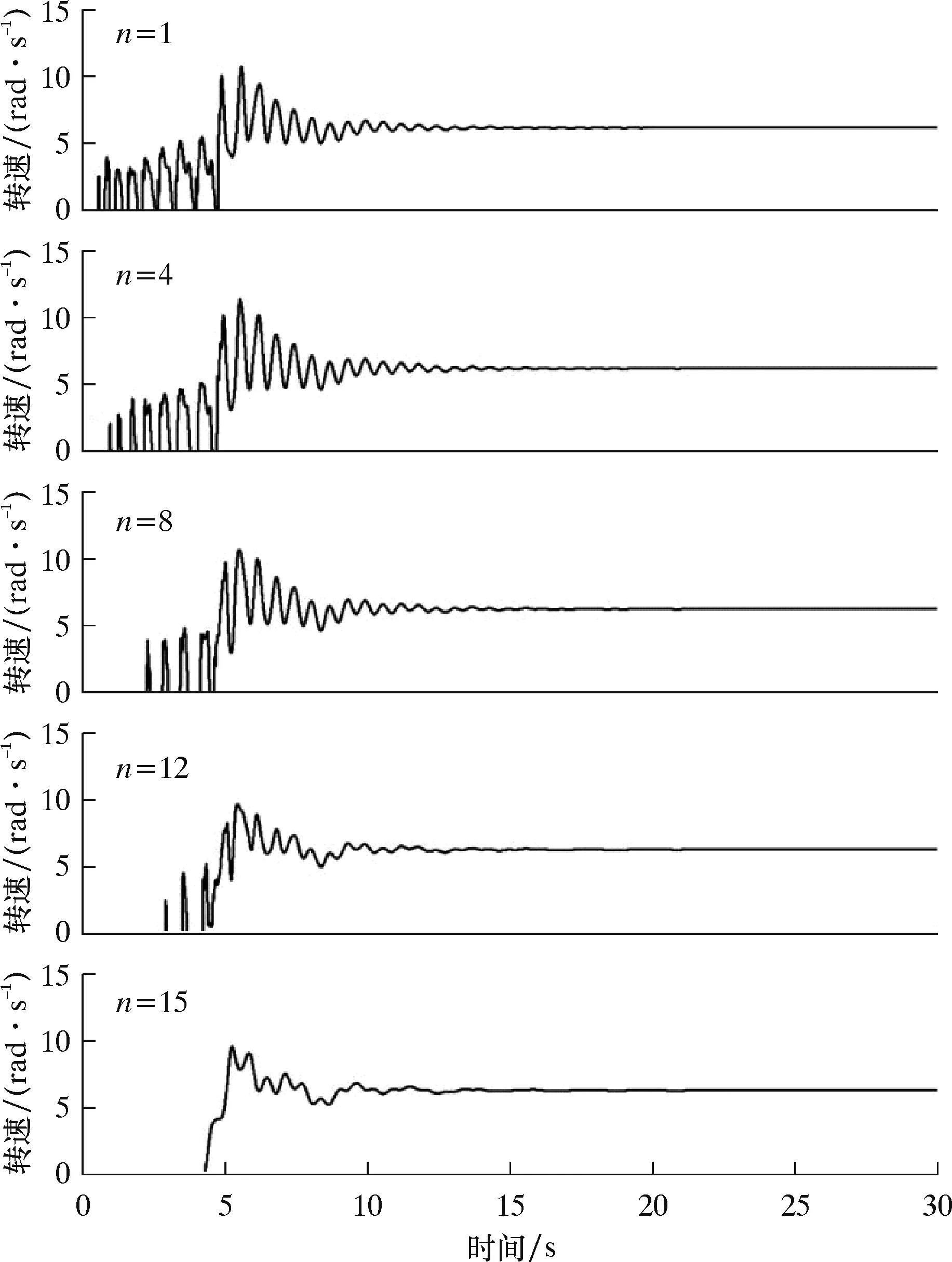
图3 水平段管柱转速随时间的响应特性曲线(转盘转速为2π rad/s)

图4为钻头的动力学响应曲线，左图表示钻头转速的时间响应曲线，右图为钻头的相轨迹曲线。从图4可以发现，钻头在起始阶段始终保持黏滞状态。这是因为井口转盘扭矩传到井底需要一段时间，在钻头启动之后，转速发生了一个小幅波动之后就保持匀速运动状态。从钻头的相轨迹曲线也可以看出，钻头角位移与井口转盘的角位移差值也不大，且钻头轨迹最后都收敛到一个点。

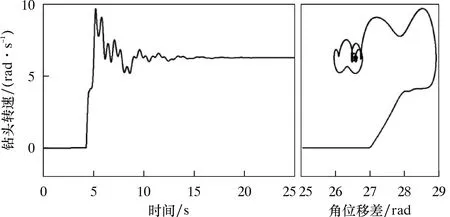
图4 钻头转速随时间的变化曲线与钻头的相轨迹曲线(转盘转速为2π rad/s)

图5为井口转盘输出扭矩随时间的变化曲线。从图5可以发现，转盘在启动时刻就存在扭矩，这是因为转盘以恒定速度启动，由于阻尼作用，所以此时都会存在一个阻尼扭矩，即无论管柱在此时是否发生了扭转变形，转盘输出扭矩已经不再为0。随着转盘输出扭矩的进一步增大，扭矩在峰值处发生一个小幅下降，最后保持了恒定的输出扭矩，此时，整个钻柱系统都保持匀速稳定运行。

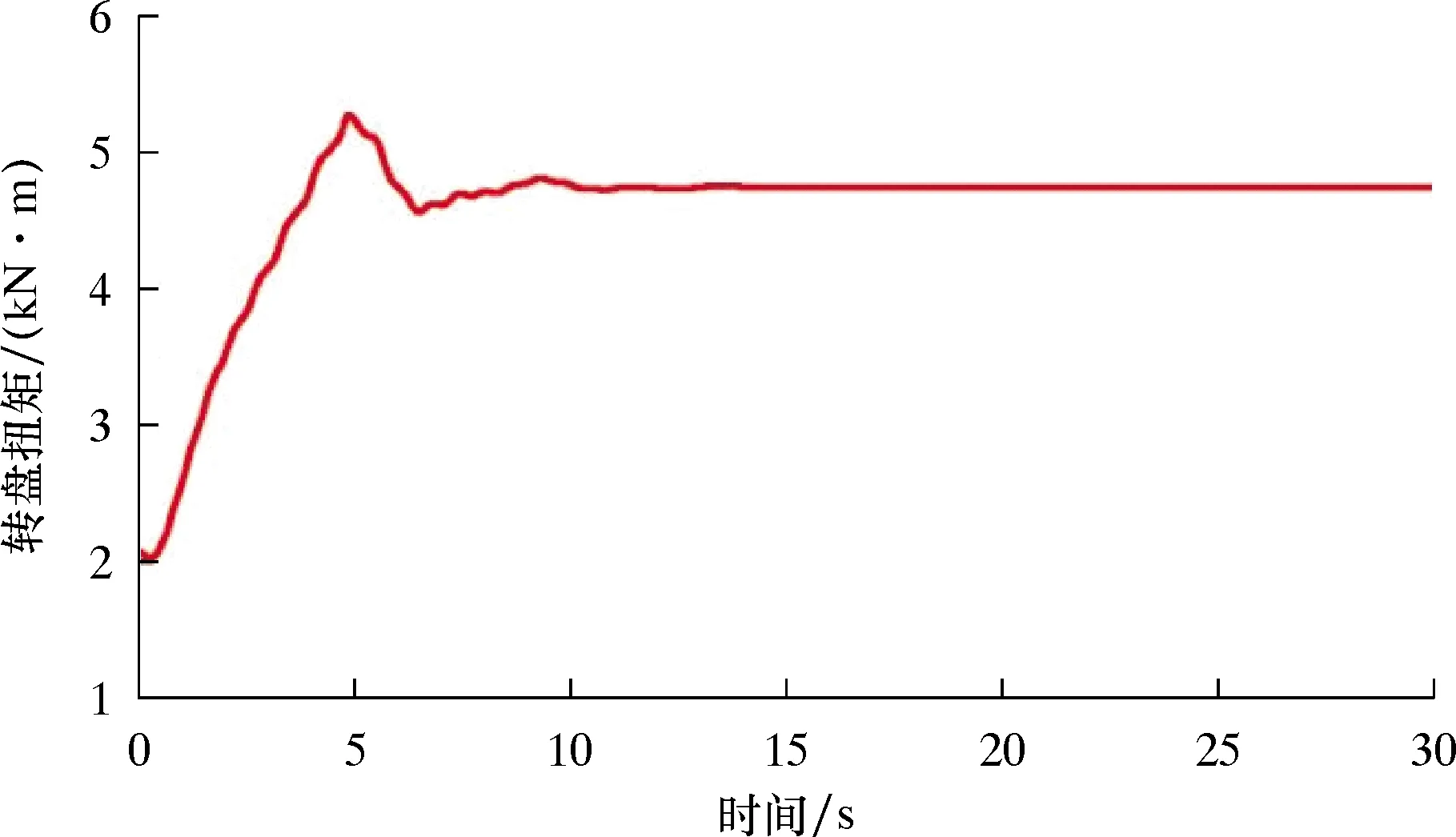
图5 转盘输出扭矩随时间的变化曲线(转盘转速为2π rad/s)

随后，对转盘转速为π rad/s时钻柱系统动力学响应进行了分析。图6为直井段管柱和造斜段管柱的扭转方向动力学响应。从图6可以看出：直井段管柱在启动阶段转速在小幅波动，但造斜段管柱在起始阶段发生了黏滑振动；随着转盘扭矩的进一步增大，直井段转速波动也随之增大，且造斜段管柱的扭转振动更加剧烈，且在一定时间内垂直段和造斜段管柱的扭转振动都未发生明显的衰减。

图6 直井段及造斜段管柱转速随时间的变化曲线(转盘转速为π rad/s)

图7为钻柱系统水平段管柱转速随时间的响应特性曲线。从图7可以看出：所有的集中质量单元都发生了黏滑振动，且距离井口最近的管柱黏滑振动最剧烈；而距离井口越远，黏滑振动的剧烈程度会越低；当n=1时，其最高转速达到了10 rad/s，为井口转速的3倍；n=15的质量单元距离井口最远，其扭转振动幅值为6.5 rad/s，约为井口转速的2倍；管柱距离井口越远，启动越慢，且在启动阶段波动量依然是离井口越近，波动越剧烈。

图7 水平段管柱转速随时间的响应特性曲线(转盘转速为π rad/s)

图8为钻头的动力学响应曲线。从图8可以发现：钻头在起始阶段始终保持较长时间的黏滞状态，这是因为井口转盘扭矩传到井底需要一段时间，在钻头启动之后，转速发生了一个小幅波动之后，转速开始发生较大幅度的波动，最高转速约为井口转速的2倍；且钻头在部分时间内发生了反转现象，这是由于钻柱系统发生扭转振动时，钻头端由于无足够大的反作用扭矩，而发生黏滑后钻头的角位移相对钻杆有一个较大的超前量，随后钻头就会发生反转；随着角位移差的变化，钻头的相轨迹并没有收敛到一个点，而是发生了周期性振动。

图8 钻头转速随时间的变化曲线与钻头的相轨迹曲线(转盘转速为π rad/s)

图9为井口转盘输出扭矩随时间的变化曲线。从图9可以发现，转盘输出扭矩在启动阶段已经开始发生小幅度的振动上升，随着转盘的输出扭矩进一步增大，扭矩在峰值处发生一个小幅下降后，始终处于较小的波动状态。

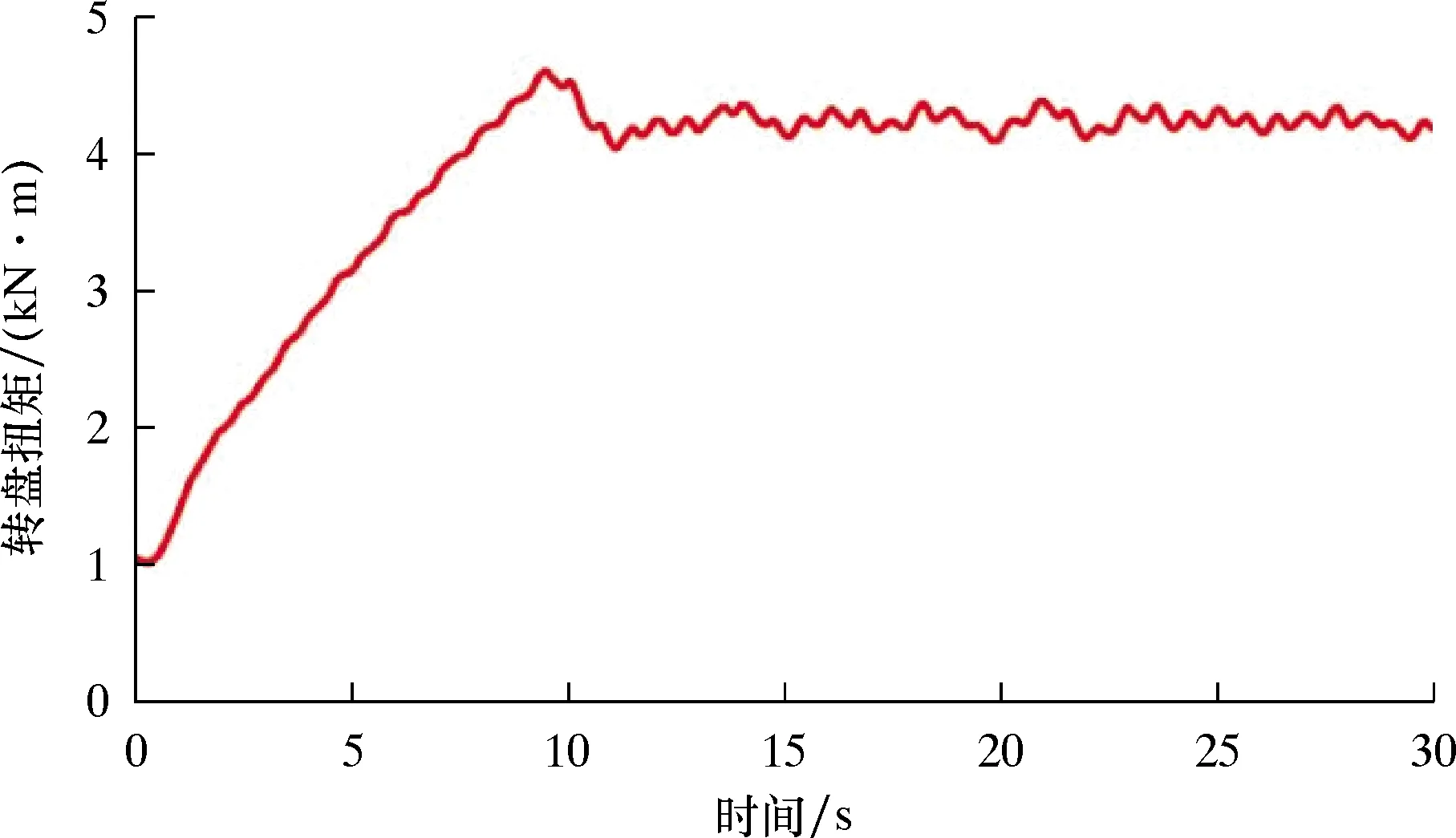
图9 转盘输出扭矩随时间的变化曲线(转盘转速为π rad/s)

通过对钻头提离井底工况进行分析，发现管柱与井壁的摩擦扭矩会诱导钻头发生较大幅度的扭转振动。根据分析结果，管柱距离井口的位置增加，扭转振动会减弱，但从分析结果看，扭转振动的幅值依然达到了井口转速的2倍左右，所以有必要分析钻柱与井壁摩擦诱导的钻头黏滑振动。

3 结 论

(1)钻柱系统与井壁间的非线性摩擦作用诱导了钻柱系统发生黏滑振动；井口转速增大，能够有效抑制钻柱系统的黏滑振动。

(2)随着转盘扭矩的增大，直井段转速波动随之增大，造斜段管柱的扭转振动更加剧烈，且造斜段入口管柱的黏滑振动强度明显大于水平段管柱。