基于GSA算法的机器人静态路径规划研究
杨坤,程鹏
(1.沈阳工学院,辽宁 抚顺 113122;2.沈阳理工大学,辽宁 沈阳 110159)
0 引言
机器人路径规划一直是学术界追踪的热点问题,其核心目标是身处存在阻碍的环境中,如何给机器人找出一条路径,使其既能够避开障碍物,又能够到达指定目标位置。需要考虑到如何获取环境信息、如何表示环境、如何进行路径执行以及如何获取知识等多方面内容。
路径规划可以分为在线路径规划和离线路径规划。前者是一种基于传感器信息的环境未知的路径规划方法,并且必须在线规划路径。后者是基于环境的全局路径规划,适用于静态环境的先验完整信息,并且必须离线规划路径。静态路径规划意味着机器人工作所在的环境是已知的且是静态的。在机器人移动之前,路径的选定是依照既定的环境信息进行规划的,择出最佳路径后,使机器人沿着选定路径从始发点到目的地。一般来说,可选路径的数目不只一条。在实际应用中,通常需要在某种特定情况下选择出一条最佳路径。通用标准包括最短路径,最短用时以及最低能耗[1-2]。此外,为了提升机器人在路径规划方面的效率并更好地满足实时性要求,通常将遗传算法和模拟退火算法引入机器人的静态路径规划和设计中。遗传算法虽然可以从概率的角度随机找到全局最优解,而模拟退火算法能够去除局部最优解,恰好弥补了遗传算法局部寻优差的弊端。因此,遗传算法与模拟退火算法的联合是解决静态路径规划问题的一种方法。
1 遗传模拟退火算法
遗传模拟退火(Genetic Simulated Annealing,GSA)算法是将遗传算法和模拟退火算法相结合的一种优化算法。它不仅包含遗传算法的并行性和全局性,而且包含模拟退火算法的退火性和局部搜索能力。GSA算法的基本流程:
(1)参数的选取:群体规模为n,遗传代数最值为N,初始温度T=T0。
(2)初始温度变更次数l=0,0代种群Pl(k),k=0。
(3)对现有种群执行以下步骤,直至产生下批种群。
①在初始群体Pl(k)中算出适应函数fi(t1);依据适应函数的概率分布从Pl(k)中选n个染色体形成种群Pls(k+1)。
②按常规遗传算法对染色体种群Pls(k+1)交叉,得到种群Plc1(k+1);在种群Plc1(k+1)中参与交叉操作的单值i和单值j,接收概率Pi和Pj如式1和2所示。经迭代,生成新种群Plc1(k+1)。
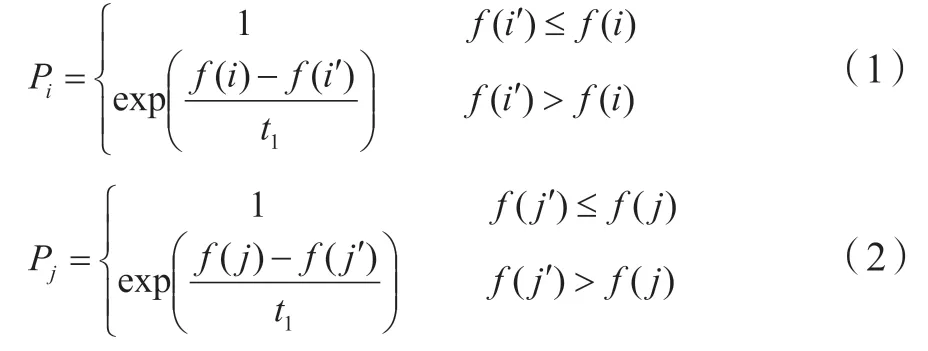
其中,种群Pls(k+1)中某单值i的目标值是f(i),种群Plc1(k+1)中某单值i的目标值是f(i');种群Pls(k+1)中某单值j的目标值是f(j),种群Plc1(k+1)中某单值j的目标值是f(j')。
③根据常规遗传算法对种群Plc(k+1)进行再变异获得Plm1(k+1);然后依公式(2.1)中的概率对变异后的个体进行接受,生成新种群Plm(k+1)。
④Pl(k)=Plm(k+1),k=k+1。观测遗传代数,若代数为N,则转到步骤③,若小于N,则转向步骤①。
(4)将温度变更,tl+1=d(t1),Pl1(k)=Pl(k),l=l+1,k=0。如果满足条件,停止,输出最优解;不满足,则转向步骤①。
2 机器人的静态环境建模
环境建模是机器人通过控制传感器感知外部环境,从而建立适合于描述外部环境的数学模型的过程。关键在于障碍物的表示,通常可以预测全球环境数据。环境建模利用数学模型来概括已知机器人的视角。环境建模是机器人进行路径规划和规避障碍的核心操作。路径规划方法中,被专家学者最为关注的方法之一就是网格解耦方法,它将机器人的能动空间划分为若干简单的网格,进而形成一个连接图,在该图上搜索从起始网格到目标网格的路径。该方法可以确保只要在起点和目标点之间存在一条路径,就可以完整地搜索该路径[4-5]。
假定机器人处于二维工作空间内,障碍物的大小、所在坐标以及各项参数均保持不变,将此二维工作空间分成等大的网格,其面积限制在机器人可以自由移动的范围。若是网格中不存在任何阻挡,则为自由网格;否则称为障碍网格。网格由自由网格和障碍网格组成。机器人环境工作空间建立如图1所示。图中黑色区域是障碍网格。
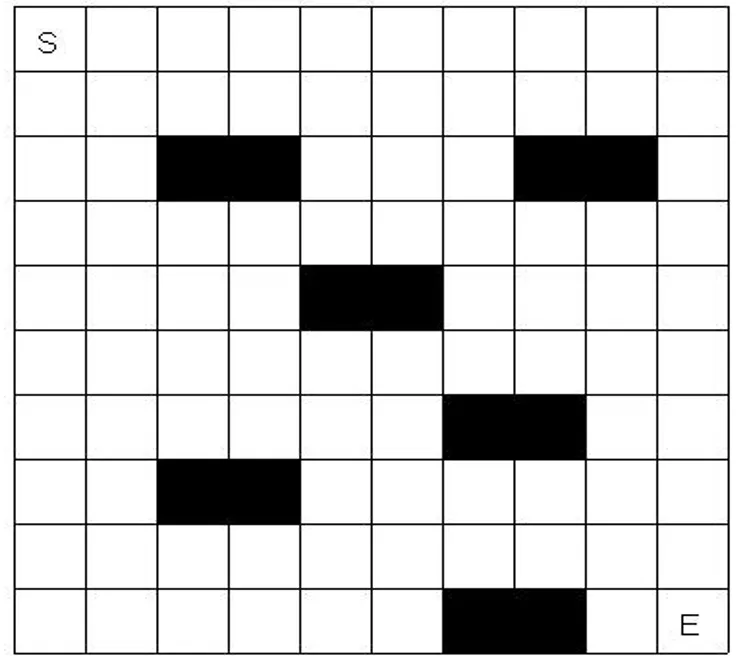
图1 机器人环境的建立
3 路径规划方法设计与仿真
3.1 路径规划求解流程
图2所示为基于GSA算法的路径规划问题求解过程。其流程可用下述步骤来描述[5-6]。
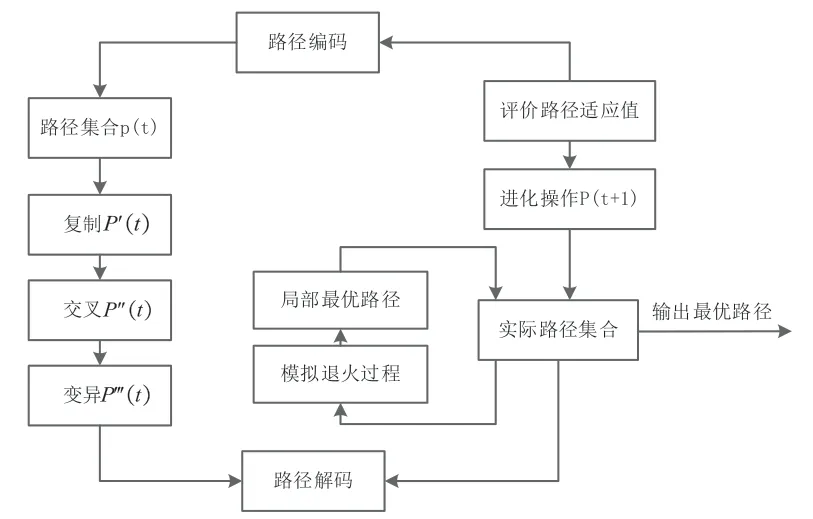
图2 GSA算法的路径规划问题求解过程
步骤1:遗传代数t初始值设为0;初始路径集合选用随机P(t)。
步骤2:选定初始路径值T=max。
步骤3:评价P(t)中各条路径的适应值
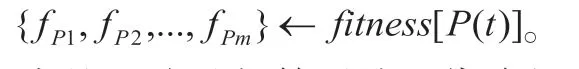
步骤5:由交叉算子进行子代路径交叉操作
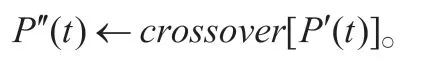
步骤6:由变异算子进行子代路径变异操作
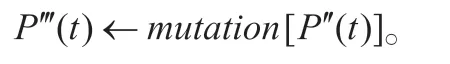
步骤7:评价P''(t)中各条路径的适应值
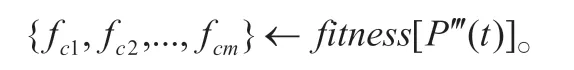
步骤8:假设上述遗传操作是由P(t)中的父代路径PI和PJ生成:P''(t)中的子代路径CI和CJ(I,J=1,2,...,M),选定概率Pi和Pj,将PI、PJ设为新路径,选定概率(1-Pi)和(1-Pj),将CI和CJ设为新路径,进而产生单代遗传后的新路径
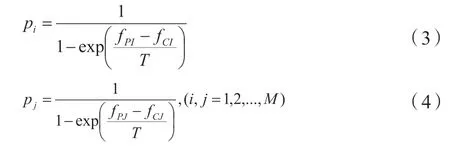
步骤9:由择优选择模型保留最佳路径
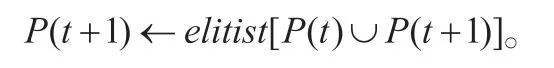
步骤10:停止判断条件。若不满足停止条件,则根据降温表设定温度T,t=t-1,返回步骤3。
当达到停止条件或增加到设定迭代次数时,即可获得当前最佳路径,算法结束。
3.2 仿真结果
为了验证所提出方法的合理性和正确性,本文以Visual C++6.0为仿真工具,设M为种群个数,值为50,Pc为交叉概率,值为0.6,Pm为变异概率,值为0.01,n为编码长度,值为16,即选用16个点构成单路。图3和图4分别为迭代4次和5次时的仿真结果,路径规划最优曲线如图所示,该路径无尖峰点,已知障碍物大小、方位及其参数不变。
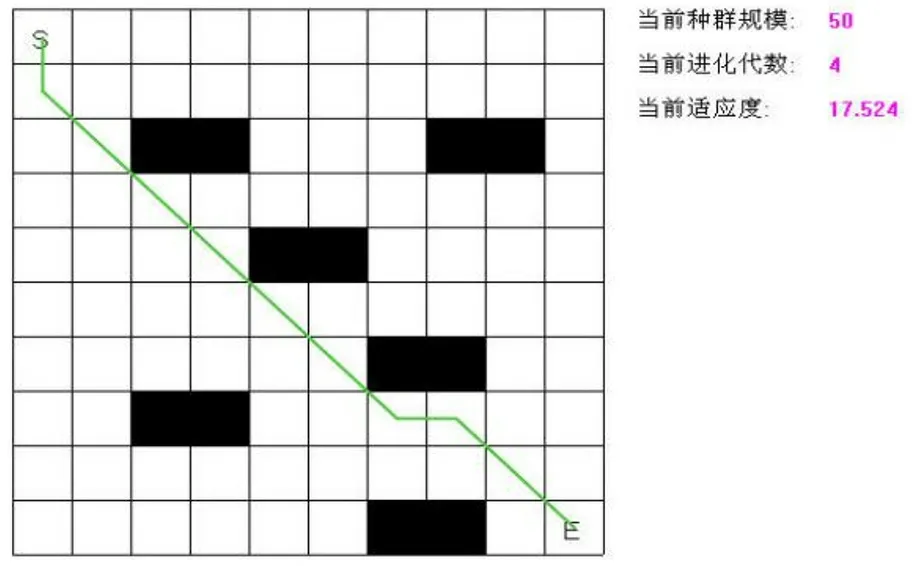
图3 迭代4次对应的路径规划结果
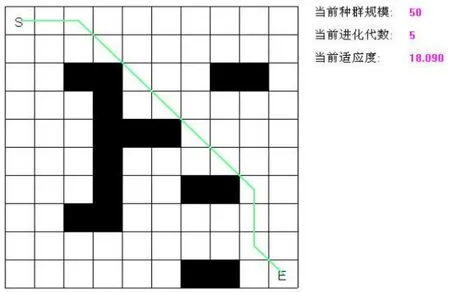
图4 迭代5次对应的路径规划结果
4 结语
在对机器人传统路径规划算法进行分析的基础上,实现机器人静态路径规划利用了GSA算法,验证了该方法的合理性和正确性,为后续机器人领域的研究提供了技术支撑。

