基于边值多值决策图的多状态系统可靠性评估方法

李焕，徐立立，杜胜杰，张明，明志茂

（广州广电计量检测股份有限公司，广东 广州 510656）

0 引言

随着现代社会对产品可靠性要求的提高，很多系统通过增加系统单元备份来提高可靠性水平，如计算机服务器系统，通信系统，水、气和电力分配系统。对于这样的系统，当一个单元故障发生时，系统仍可在可接受的或者降级的状态继续工作，体现出多性能状态特性。因此如何表征系统的多性能状态特性逐渐成为可靠性理论研究的重点，表征多状态系统的可靠性模型也层出不穷。

针对多状态系统的可靠性评估，研究人员已经提出了多种多状态系统的可靠性建模和评估方法。其中MDD模型是从传统的二元决策图（Binary Decision Diagram，BDD）扩展而来的解决多状态系统的有效方法，已经得到了广泛地研究。但是，当系统状态数量较多时，MDD模型的规模会急剧增长。针对这种情况有学者提出了EVMDD模型，该模型能够降低MDD模型的复杂度[1]。

但是目前的EVMDD模型都是由MDD模型转换而来，实际应用中仍然需要先构建MDD模型，对于节点多、状态多的系统构建MDD模型的过程将特别复杂，这也限制了EVMDD在实际工程中的应用。本文研究一种直接构造EVMDD的方法，不需要先构建MDD模型可以直接生成EVMDD模型，对具有节点数量多、系统状态多的复杂多状态系统分析更加高效。

1 概述

最近，人们引入了不同的多状态模型来表示各种多状态系统的恶化过程，如计算机服务器系统、电信系统、水、气、配电系统。这些数学方法可以分为两类:基于状态空间的方法和组合方法。多值决策图是结构函数的一种紧凑表示形式。MDDs作为一种解决多状态系统的有效方法，在许多文献中得到了广泛的研究。此外，还提出了基于扩展形式的MDDs，以减少节点的数量。通过给边缘赋值，比MDDs具有更紧凑的形式。Nagayama提出了EVMDDs中边缘数的最小化算法，用于多状态系统的快速分析。通过引入EVMDDs约简规则，进一步提高了计算速度[2]。

本文提供了一种不需要从MDD转换即可直接构造EVMDD进行多状态系统可靠性评估的方法。本文的目的和解决的问题是：根据系统的结构函数，直接构建多状态系统的EVMDD模型，评估系统可靠性。该方法首先分析系统结构特征，构建系统的结构函数，并以表格形式表示。之后，根据本文提出的直接构造EVMDD的方法，得到多状态系统的可靠性评估模型。构造EVMDD的核心思想是如何计算EVMDD边值，系统的状态由从根节点到终端节点的边值之和表示。因此，我们可以使用深度优先搜索并假定初始值来获得完整的EVMDD。当完成一条路径的遍历时，边值之和应等于系统的状态。如果值不相等，则反向更新边值。最后，利用本文提出的构建方法，对于多状态系统可靠性进行评估。

2 评估方法

本文提出的直接构造EVMDD的多状态系统可靠性评估方法主要包含以下四个部分。

2.1 根据系统的多性能水平状态，构建系统的多值结构函数

构造多状态系统的结构函数就是构造组件状态与系统状态之间的各种映射。结构函数可以用表格、解析式或算法表示。本文中为了显示直观，用表格表示多状态系统的结构函数。下面说明结构函数的具体构建步骤：

步骤1：确定系统、分系统和单元的任务目标，分别监测系统、分系统和单元的降级过程，并将其具有的明显功能降级的各个状态用离散的数值进行表示。如一个包含n个组件的多状态系统，向量表示所有n个系统组件的状态；系统共有m个状态：从系统最佳状态（m-1状态）到系统完全失效（0状态），在一些研究中m也被称作多状态系统的可靠性水平。每个系统组件有m个状态每种状态的概率为：

多状态系统的可靠性（状态）取决于组件状态和系统的结构函数：

步骤2：若系统、分系统和单元的状态监测数据是连续值，则需要根据不同的数据范围与步骤1中定义的离散状态值建立映射关系，即用一个离散的值表示单元性能的某个区间值。若系统、分系统和单元的状态监测数据本身是离散值，则直接与步骤1中的状态值建立一一对应关系即可。这样就可以得到多组单元、分系统和系统的状态组合关系，将这些组合关系以表格的形式进行表示，表中的每一行表示了一种组合关系。

在实际应用中，一个组件的退化会影响系统的性能，即使系统不会立即发生明显退化，所以多状态系统的结构函数可以看作一个单调递增函数。

2.2 根据系统的多性能水平状态，构建系统的多值结构函数

本文采用深度优先和假定初始值的方法来获得多状态系统的EVMDD模型。每条路径边值之和就是系统的一种状态。判断得到的边值是否与结构函数表中系统状态值对应，如果不对应就反向更新边值，直到等于系统状态值[4]。

首先给出方法构建中所应用相关符号的定义：

ti是第i个组件的状态空间

si是ti确定的系统状态值，

ni是ti中的状态数量；

L是组件状态与系统状态之间的映射关系的数量；

pi是EVMDD中一条路径；

wij是路径pi的第j个节点的权重值；

k是一个临时变量；

i是下标变量；

根据EVMDDs的特点和多值函数的定义，可以得出EVMDD的构建过程包括以下七个步骤：

步骤1：设初值：令i=1；

步骤2：当i＞L时，过程结束；否则转第三步；

步骤3：根据结构函数构造EVMDD的第i条路径；令k=ni，如果组件状态是0，将0赋值给节点引出边的边值；否则赋值为1；

步骤5：根据系统状态更新路径pi的边值。如果第k边的值是0，转步骤6；否则通过下面的公式验证权值：然后转步骤7；

步骤6：令k=k-1，返回步骤5；

步骤7：判断节点的所有的边是否都构造完成，如果已经完成，判断节点是否已经存在。如果节点已经存在，删除节点并让引进的边连接到已经存在的节点。然后令i=i+1并返回步骤2。

2.3 应用两个简化规则减少EVMDD模型节点的数量，提高计算效率

规则1：共享子图

当2个节点引出边的边值完全对应相同，且所有的边连接到相同的节点或者对应相等的系统状态值的情况下，这两个节点就是完全相同的，可以简化为一个节点。

规则2：删除满足以下两个条件的非终端节点，并将指向已删除节点的边重新指向节点V。

（1）它的引出边都指向同一个节点V；

（2）所有引出边的边值都为0。

两个条件需同时满足才可以进行删减节点。

2.4 EVMDD模型进行多状态系统的可靠性评估

多状态系统可靠性与系统当前性能水平有关，多状态系统可靠性计算使用下面的公式：

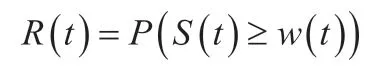
s(t)表示系统当前性能水平下的状态，s(t)表示系统的性能需求。本文中将系统的连续性能指标离散化，与离散的系统状态进行映射。

3 具体实施方式

实施方式说明：提供了一种基于系统、分系统和单元的状态监测数据自动学习系统可靠性模型和失效参数，并对系统进行可靠性进行评估的方法，具体实施方式说明如下。

3.1 构建多状态系统的结构函数

通过对系统每个单元所包含的不同状态进行分析，进而得到整个多状态系统的结构函数。下面结合具体实例进行说明：

一个多状态n中取k系统，由三台热电联产机组组成的区域电力和供热系统，可同时产生电力和热能，该系统为负荷提供电能和热能。在该系统中在该系统中，G1是一个GPC-180D气体单元，G2和G3是GPC-70D气体单元。三个燃气机组的额定发电能力列于表1。

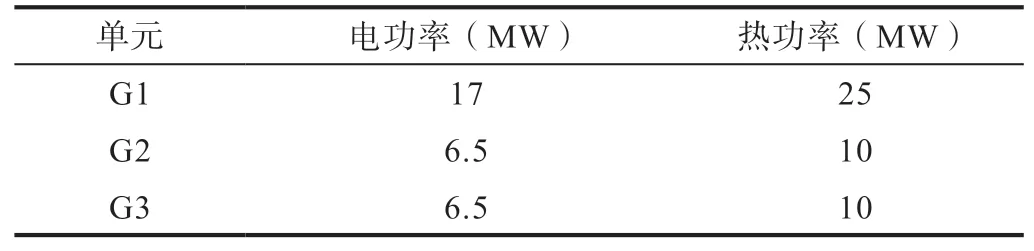
表1 各单元发电能力参数表

每个发电机组包含三种状态：0；1；2，三种机组状态对应的性能等级及该性能水平发生概率如下表格2所示：

表2 G1机组的三种状态的性能参数及每种状态发生概率

表3 G2机组的三种状态的性能参数及每种状态发生概率

表4 G3机组三种状态的性能参数及每种状态发生概率

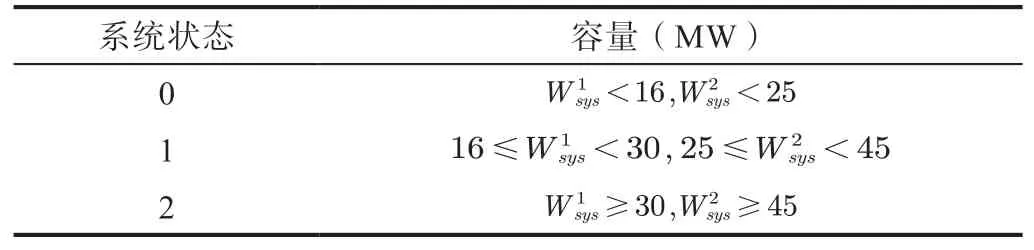
表5 电力和供热系统的容量分配

因此，对应多状态系统的结构函数可以由系统中每个单元的状态组合得到，如表6所示：

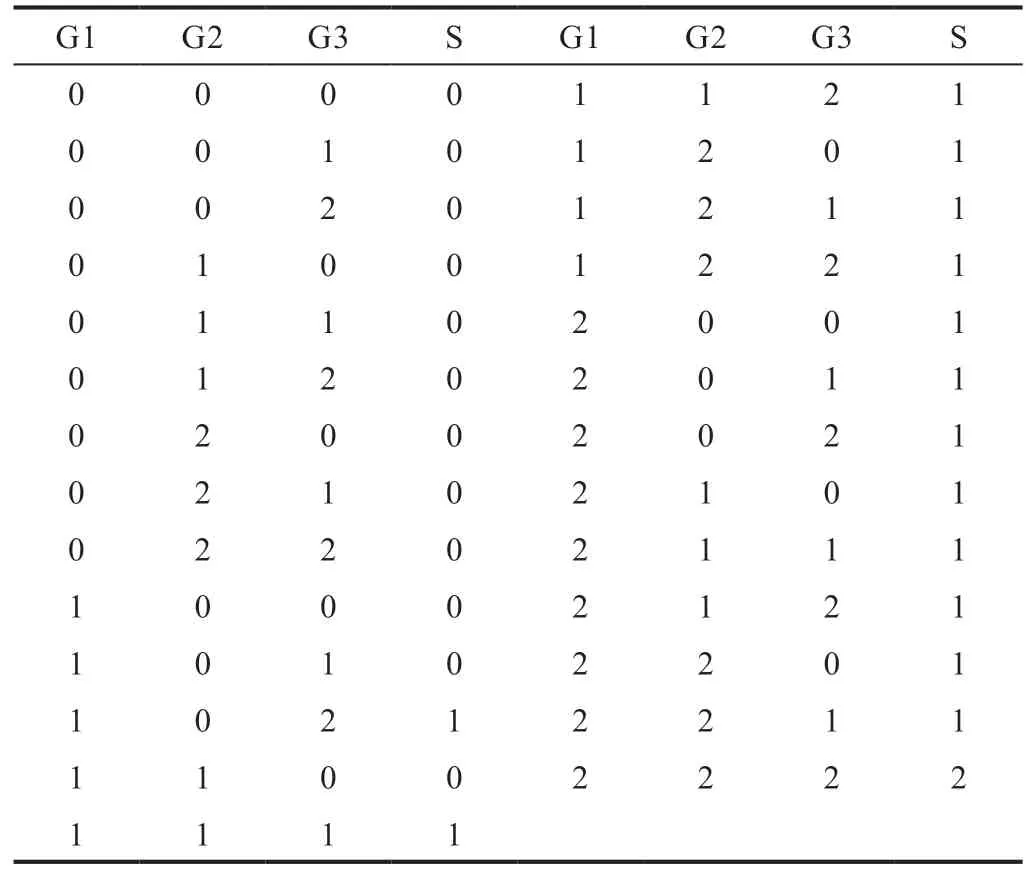
表6 热电系统结构函数

3.2 建系统的EVMDD模型

本文采用深度优先和假定初始值的方法来获得多状态系统的EVMDD模型。通过遍历每条路径，得到相应的边值，每条路径上的边值之和对应多状态系统的一种状态。判断路径的边值之和是否与结构函数表中系统状态值对应，如果不对应就反向更新边值，直到等于系统状态值就完成当前路径，继续下一条路径[5]。

ti是第i个组件的状态空间

si是ti确定的系统状态值，

ni是ti中的状态数量；

L是组件状态与系统状态之间的映射关系的数量，L=27；

pi是EVMDD中一条路径；

wij是路径pi的第j个节点的权重值；

k是一个临时变量；

i是下标变量；

具体构建步骤描述如下：

步骤1：设定初值：令i=1；

步骤2：当i＞L时，过程结束；否则转第三步；

步骤3：根据结构函数构造EVMDDs的第i条路径；令k=ni，如果组件状态是0，将0赋值给节点引出边的边值；否则赋值为1；

步骤5：根据系统状态更新路径pi的边值。如果第k边的值是0，转步骤6；否则通过下面的公式验证权值：然后转步骤7；步骤6：令k=k-1，返回步骤5；

步骤7：判断节点的所有的边是否都已经构造完成。若已经完成，判断节点是否已经存在。若节点已经存在，删除节点并让引进的边连接到已经存在的节点。然后令i=i+1并返回步骤2。

3.3 减少节点数量、提高算法效率

依照上述步骤遍历结构函数表格中所有向量，构建出系统所有路径，并应用两个简化规则，将相同子图保留一个，删除对系统无影响的节点，对EVMDD进行简化，最终得到多状态系统的EVMDD结构

3.4 EVMDD模型进行多状态的可靠性评估

根据n中取k多状态系统中每个机组的状态概率分布（表7），可以得到多状态系统在不同状态下的联合概率分布，如表7所示：

表7 多状态系统状态概率分布表

则该n中取k的多状态系统的可靠度是0.89925

4 结语

本文提出了一种直接从结构函数构造EVMDDs的方法，而不是使用MDDs。对于具有大量系统状态的大型多状态系统，该方法非常方便有效。此外，为了减少时间开销，本文还介绍了一种基于EVMDDs的并行分析算法。该算法很容易在当前的并行框架或库中实现。通过对并行算法和直接算法效率的比较表明，随着构件数量和系统状态数的增加，并行算法比直接算法具有更大的优势。

本文提出的算法没有考虑变量的阶数，因为阶数会影响EVMDDs的大小。在以后的工作中，我们将研究变量的顺序和evmdd的大小之间的关系。