青少年篮球运动员选拔系统的研究——基于模糊综合评价模型

沈继东

(集美大学体育学院，福建 厦门 361021)

篮球运动由于对场地条件要求低，以及身体对抗激烈，在全世界范围内得以广泛的普及和开展。篮球运动包括了跳、跑、投等运动形式，在参与篮球运动的过程中，参与者不仅在身体素质和人体机能方面得到充分的锻炼，而且起到了保持生命活力的作用，为其他生命活动打下坚实的物质(身体)基础，达到了提高人们的生活质量的积极作用。青少年篮球运动员作为国家篮球运动员的后备人才，需要客观合理的选拔系统才能保证篮球运动的可持续发展，这也是振兴篮球运动的前提条件。

我们应该如何来选拔青少年篮球运动员呢？这就涉及到如何客观准确评价一个青少年篮球运动员竞技能力的问题。什么样的运动员能被称为优秀的呢？日常生活中经常会听到球迷评论一个篮球运动员的好坏，但是篮球运动员的评价并不是简单的好或者坏可以概括的，具体到细节就是每一个篮球运动员场上位置和所擅长的技能不同，不同的运动员有自己的优势和特点，有些运动员擅长投篮，有些运动员防守方面比较出众，如果评价只是采用 “很好、好、一般、差”等自然语言来描述，那么自然语言的模糊性使得我们无法准确地判断运动员们到底有多好、好到什么程度。利用模糊数学[1]的理论和方法，恰恰能够使模糊、定性的评价转变成为数学、定量的评价。本文结合多年一线青少年篮球培训的经验，摒弃传统的定性分析或单因素评价的方法，利用文献资料法、问卷调查、专家咨询及数理统计的方法，构建基于多因素多层次模糊综合评价模型的青少年篮球运动员选拔系统。主要分为以下几个步骤：

(1)分析影响青少年篮球运动员竞技能力的主要因素，构建评价青少年篮球运动员的多因素多层次指标体系；

(2)利用专家评议法，确定影响不同位置篮球运动员竞技能力的因素重要程度模糊集；

(3)构建基于多因素多层次模糊综合评价模型的青少年篮球运动员选拔系统。

基于模糊综合评价模型的青少年篮球运动员选拔系统，能为选拔青少年篮球运动员提供更加客观准确的方法，使运动员选材更科学化，且可操作性更强。

1 青少年篮球运动员竞技能力分析

所有专项运动的关键部分都是竞技能力，即篮球运动员在参加比赛和训练时所具备的能力。篮球运动员的竞技能力主要是由体能、技能以及心理能力三部分构成，每一个部分又分别由多个具体的要素组成。简单来说，篮球运动员竞技能力是保证机体在快速持续的高强度的比赛中所需的体能，将身体运动和球完美地相结合所需要的出色技能，确保稳定发挥的运动员心理调节能力和智能，运动个体与整体需要的战术协调能力的完美结合，这几个方面的有机统一。

由于青少年篮球运动员还处于生长发育阶段，各项身体机能指标还处于不稳定状态，所以其竞技能力有其自身的特殊性。在2019年全国篮球后备力量冬训营时，中国篮球协会将我国青少年篮球运动员分为两个年龄层次：13～15周岁为少年运动员，16～18周岁为青年运动员。根据体育总局青少司主编的《中国青少年篮球训练教学大纲》[2]，15岁以下年龄段的中国篮球运动员在进行选拔时不区分球场位置。

通过研读前人对于篮球运动员竞技能力的调查和相关研究，得到了许多有用的理论知识，初步了解了篮球运动员的竞技能力构成、篮球运动员的体能结构和篮球场上角色的相关性等。孙义良[3]对篮球运动员的竞技能力构成、体能结构及其场上角色的相关问题进行了论述。黄新章[4]以篮球运动员中的核心后卫这一位置为研究对象，以身体形态指标、攻防量化指标、运动智能、赛场心理等因素指标为研究对象进行比较，分析了参加2008年北京奥运会男子篮球队的众多核心后卫的竞技能力水平，尤其是针对我国男子篮球核心后卫的研究，旨在寻找我国后卫与国外后卫的差距，以此为我国男子篮球核心后卫的人才培养和后期训练提供参考。毛华平[5]以长三角地区高中男子篮球运动员作为研究对象，分析我国青少年篮球运动员竞技能力各个核心指标的水平和特点。熊磊[6]运用科学的方法构建了篮球运动员竞技能力评价指标体系，确立了评价指标的权重，较为全面、客观地制定了评价的方法。张战毅[7]等构建了我国青少年男子篮球运动员专项体能指标与评价体系。

2 构建青少年篮球运动员竞技能力模糊综合评价模型

构建篮球运动员竞技能力模糊综合评价模型，首先需要确定影响青少年篮球运动员竞技能力的因素指标以及对应的评价集，构建因素重要程度模糊集A，然后构造出模糊综合评价矩阵R，根据得到的R利用不同的模型确定模糊评价集B，最后得到综合评价。

2.1 因素指标集以及评价集的选取

运动员竞技能力[8]指的是运动员在参加比赛的过程中表现出来的包括体能、技能、战术能力、运动智能以及心理能力的综合能力。影响篮球运动员的竞技能力的因素是多方面的，在第一部分的分析以及阅读大量相关文献[9-10]和资料后，将理论与实际相结合，总结出青少年篮球运动员的竞技能力结构，它可以被划分为四个部分：进攻能力、防守能力、身体素质、精神意志能力,详见表1。

表1 青少年篮球运动员竞技能力模糊综合评价影响因素表

2.2 构建因素重要程度模糊集A

在进行模糊综合评价时，必须给出各个因素在总评价中的重要程度，我们称之为因素重要程度模糊集A。因素重要程度模糊集A的确定是否恰当直接影响综合评判的结果。

设因素集为：

U={u1,u2,…,um}，

U的因素重要程度模糊集为：

A=(a1,a2,…,am)。

本文中使用Delphi法(专家评议法)来构建因素重要程度模糊集A。Delphi法[1]是利用专家集体智慧来确定各因素在评价问题中的重要程度系数ai(i=1,2,…,m)的有效方法之一。

本文为了确定各因素的重要程度系数，邀请了13位一线青少年篮球教练进行评议，确定各个指标的因素重要程度集。以进攻能力指标U1为例，确定其因素重要程度模糊子集A1，计算步骤如下：

(1)确定U1各因素u1j(j=1,2,3,4)的重要性序列值

专家们凭个人的经验和见解，确定各因素u1j的重要性序列值e1j，j∈{1,2,3,4}。对最重要的因素，取e1j=m，对最次要的因素，取e1j=1。将第k位专家就因素u1j所给定的因素重要性序列值e1j(k)。这里给出第k位专家所提供的一份e1j值的评定表，见表2。

表2 第k位专家的e1j评定表

(2)编制优先得分表

e11(k)=4，e12(k)=3。因e11(k)/e12(k)=4/3>1，故记A1112(k)=1；而e12(k)/e11(k)=3/4<1，故记A1211(k)=0。然后按13位专家提供的重要性序列值e1j(k)，将所有参加评议的专家给出的A1112(k)和A1211(k)分别累加起来，得到：

这说明有4位专家认为因素u11比因素u12重要，而有9位专家认为因素u12比因素u11重要。其余的得分统计值见表3。由于重要性无法比较，故A1111、A1212、A1313、A1414均不存在，我们将其均记为*。

表3 U1中各元素的优先得分表

(3)求∑A1j的值

将表3中各行的累加值∑A1j记在表3中的第6列。例如， ∑A11=4，说明参加评议的专家有4人次认为因素u11比其他诸因素重要。从表2得知， ∑Amax=∑A14=35，∑Amin=∑A11=4，这说明因素u14的重要程度最高，而因素u11的重要程度最低。

(4)计算级差d

令amax=1,amin=0.1，d=

(∑Amax-∑Amin)/(amax-amin)，

则可知：

d=(∑Amax-∑Amin)/(amax-amin)=

(35-4)/(1-0.1)=31/0.9≈34.44

(5)计算因素重要程序系数a1j

根据参考文献[1]可知道计算因素重要程度系数a1j的公式为：

a1j=(∑A1j-∑Amin)/d+0.1(j=1,2,3,4)，

(1)

或

a1j=1-(∑Amax-∑A1j)/d(j=1,2,3,4)，

将表3中第6列的∑A1j值分别代入式(1)，得：

a1j=(∑A1j-∑Amin)/d+0.1=

(∑A1j-4)/34.44+0.1 (j=1,2,3,4)

然后将计算出的a1j的值填入表3中的第7列，例如：

a12=(9-4)/34.44+0.1=0.245 2

这样我们就求出所要确定的因素重要程度模糊集为：

A11=(0.1,0.2452,0.855,1)

A12=(1.9，0.71,0.1，0.158)

A13=(1，0.904,0.13,0.1)

A14=(1,0.1,0.492，0.608)

A15=(1,0.1,0.492,0.608)

利用类似的方法可求出其他位置各个指标的因素重要程度模糊集。

2.3 构造模糊综合评判矩阵U

根据多层次模糊综合评判方法，可知U的模糊综合评判矩阵R可表示为：

为了确定R，关键是确定Ri，Ai，Bi(i=1,2,3,4,5)，下面依次构造Ri，Bi。

2.3.1 构造各因素子集的综合评判矩阵Ri

同样地，以因素子集U1为例构造其综合评判矩阵。首先，对因素子集U1中的单因素u1i(i=1,2,3,4)作单因素评价，从因素u1i确定该事物对评语vj的隶属度cij，从而得出U1中第i因素u1i的单因素评价集：

ci=(ci1,ci2,

ci3,ci4)(i=1,2,3,4)，

把这4个单因素评价集作为行即得一个总的评价矩阵：

以此类推，可以得到因素子集U2，U3，U4的评价矩阵R2，R3，R4。

2.3.2 构造各因素子集的模糊综合评价集Bi

模糊综合评判模型有很多种，不同的模型有各自的优缺点及适用范围。

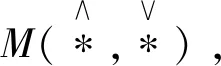
模型M(∧,∨)为主因素突出型的综合评判，其评判结果只取决于在总评价中起主要作用的那个因素，其余因素均不影响评判结果，此模型比较适用于以单项评判最优作为综合评判最优的情况。(注：采用此模型值得注意的是，因素重要程度模糊集A=(a1,a2,…,am)中的各元素ai为在考虑多因素时rij的调整系数，没有权重系数的意义)

模型M(·,∨)也是主因素突出型的综合评价，它与模型M(∧,∨)相近，但比模型M(∧,∨)精细些，不仅突出了主要因素，也兼顾了其他因素，此模型适用于模型M(∧,∨)失效(不可区别)，需要“加细”的情况，ai为在考虑多因素时rij的调整系数，没有权重系数的意义。

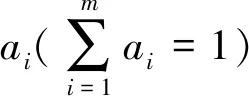
B1i=A1i*R1i=(b11,b12,b13,b14)，

B2i=A2i*R2i=(b21,b22,b23,b24)

B3i=A3i*R3i=(b31,b32,b33,b34)

B4i=A4i*R4i=(b41,b42,b43,b44)

由上述得第二层综合评判矩阵为：

(2)

2.4 确定模糊评价集B

U的因素重要程度模糊集为：

A1=(0.3109，0.344，0.3109，0.034)

A2=(0.534，0.0828，0.33，0.0534)

A3=(0.534，0.0828，0.33，0.0534)

A4=(0.0865，0.4482，0.4204，0.0449)

A5=(0.0865，0.4482，0.4204，0.0449)

B=A*R=(b1,b2,b3,b4)。

其中：

2.5 综合评判

根据最大隶属度原则，选择模糊综合评价集B=(b1,b2,b3,b4)中最大的bj所对应的语言Vj作为综合评判的结果。

3 结论

本文以13～15周岁的青少年篮球运动员为研究对象，利用文献资料法、问卷调查、专家咨询以及数理统计的方法，分析青少年篮球运动员竞技能力的主要因素，构建评价青少年篮球运动员的多因素多层次指标体系，利用专家评议法确定影响青少年篮球运动员竞技能力的因素重要程度模糊集，从而构建基于多因素多层次模糊综合评价模型的青少年篮球运动员选拔系统。相关实践分析表明，该系统可以为篮球教练员提供辅助决策，为选拔青少年篮球运动员提供更加全面、科学的方法。