基于改进粒子群算法的轮胎模型参数两级辨识

张丽霞， 刘家琪， 潘福全， 张文彩， 郑超艺

(青岛理工大学机械与汽车工程学院， 青岛 266525)

计算机仿真技术在车辆领域广泛应用，为提高分析速度，仿真分析整体模型中的部分复杂模型常采用经验模型进行替代，因此对经验模型的辨识速度和辨识精度有了越来越高的要求，对辨识方法的研究也显得尤为重要。Cabrera等[1]利用协同进化算法对轮胎参数进行辨识，该方法同样存在对初值敏感的问题。宋晓琳等[2]利用带变异阈值的粒子群算法对PAC89(Pacejka’89 tyre model)轮胎模型直接进行参数辨识，其中纵向力辨识结果较差，均方根值在1 000以上。王前等[3]采用一种新型的自适应差分进化算法对魔术公式轮胎模型进行辨识，解决了差分算法控制参数为定值的问题，辨识结果较好，但算法收敛时的迭代次数较多，计算时间长。田炜等[4]利用Excel Solver对航空器拖车的轮胎模型进行了参数辨识。边伟等[5]利用遗传算法对魔术公式轮胎模型分两级进行辨识，然而在辨识过程中，魔术公式的水平和竖向偏移被忽略，无法体现外倾角变化和帘线效应对轮胎力学特性的影响。赵凯旋等[6]利用遗传算法对汽车悬架阻尼可调减振器进行参数辨识，适应度值均小于10，辨识结果较好，且通过实验对比，验证模型准确性。Liu等[7]采用逆向遗传算法对不同充气压力下的轮胎参数进行辨识，遗传算法鲁棒性强，但收敛速度慢，辨识耗时长。Matsubara等[8]提出一种基于迭代联立方程的三维柔性环模型的辨识方法。Lee等[9]结合智能轮胎内传感器测量的信息，提出一种柔性化轮胎模型实时辨识与预测的方法。吴碧巧等[10]利用分层型免疫协同进化粒子群算法对双馈异步电机进行参数辨识，实现电机中高度非线性系统的辨识工作，结果表明其策略有很好的全局收敛性。陈鼎等[11]通过广义牛顿拉夫森算法对轮胎接地相互作用模型进行了参数辨识。

轮胎作为与地面直接接触的汽车部件，对整车的操纵稳定性有重要影响。然而由于轮胎的主要材料是超弹性橡胶材料，将轮胎完整的加入整车操纵稳定性仿真分析中时，对计算机性能要求较高，分析速度较慢。因此，在对汽车操纵稳定性进行仿真或轮胎智能控制系统的研究时，通常需要合理的轮胎数学模型来描述轮胎的力学特性。PAC89轮胎模型利用三角函数形式的公式描述了轮胎纵滑特性和侧偏特性，是一种经验模型，适用于低频路面下的稳态工况，在车辆操纵稳定性研究中被广泛应用。因此快速准确的PAC89轮胎模型参数辨识对整车操纵稳定性能分析有重要意义。

所辨识的PAC89轮胎模型具有参数多和高度非线性的特点，这是导致辨识速度慢和辨识精度差的主要原因。因此，提出一种采用加入自适应权重和自然选择性的改进粒子群算法分两级进行轮胎参数辨识的PAC89轮胎模型辨识方法。将改进的粒子群算法与两级辨识相结合，发挥两者的优点，快速得到准确的轮胎模型，并以侧偏力辨识为例，通过迭代次数和辨识精度验证该辨识方法的优越性。

1 PAC89轮胎模型

PAC89轮胎模型是魔术公式轮胎模型的早期版本，因其在操纵稳定性研究中能够快速、准确地表达轮胎力学特性而被广泛采用。图1为PAC89轮胎模型的输入输出。

图1 PAC89轮胎模型Fig.1 The PAC89 tire model

PAC89轮胎模型的魔术公式基本表达式为[12]

(1)

式(1)中：Y(X)表示纵向力、侧偏力和回正力矩，相对应的x表示滑移率和侧偏角；B为刚度因子，受曲线原点处斜率影响；C为形状因子，控制曲线形状；D为峰值因子，受曲线峰值影响；E为曲率因子，影响曲线的曲率；Sv为垂直偏移量；Sh为水平偏移量，由于帘线效应和外倾角等原因，两个偏移量一般不为零，即曲线不过原点。

以PAC89轮胎模型的侧偏力魔术公式辨识为例进行研究分析。侧偏力魔术公式为

(2)

(3)

(4)

C=a0

(5)

(6)

E=a6Fz+a7

(7)

Sh=a8γ+a9Fz+a10

(8)

Sv=a11Fzγ+a12Fz+a13

(9)

式中:Fy为侧偏力；x为侧偏角；BCD为侧偏力零点处侧偏刚度；Fz为垂直载荷；γ为轮胎外倾角；a1～a13为待辨识的二级参数。PAC89轮胎模型侧偏力辨识需要有至少3组不同载荷和外倾角下的实验数据为依据。采用205/55R16半钢子午线轮胎在不同载荷和外倾角下进行了3次侧偏角到达12°的轮胎纯侧偏工况实验，依据实验结果辨识该半钢子午线轮胎的PAC89轮胎模型。3次实验的条件如表1所示，实验结果曲线如图2所示。

表1 半钢子午线轮胎实验Table 1 Experiment of semi-steel radial tire

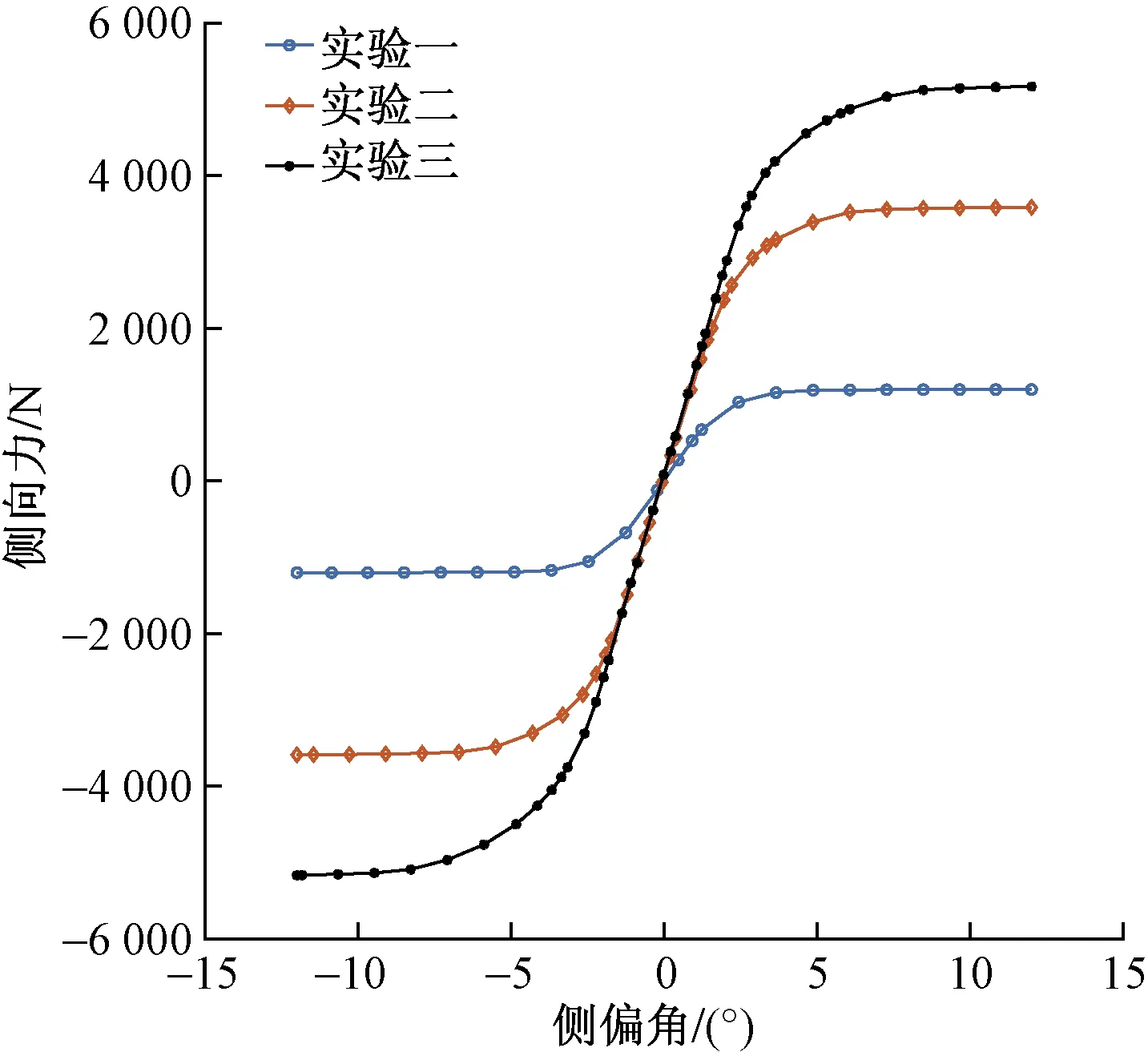
图2 侧偏力实验曲线Fig.2 Experimental curve of lateral force

2 基于改进粒子群算法的两级辨识

2.1 改进粒子群算法

粒子群算法将初始粒子群随机地分布在空间内，通过模拟种群觅食的行为规律，根据群体和自身经验来寻找整个空间中的最优解[13]。图3为粒子位置更新过程。

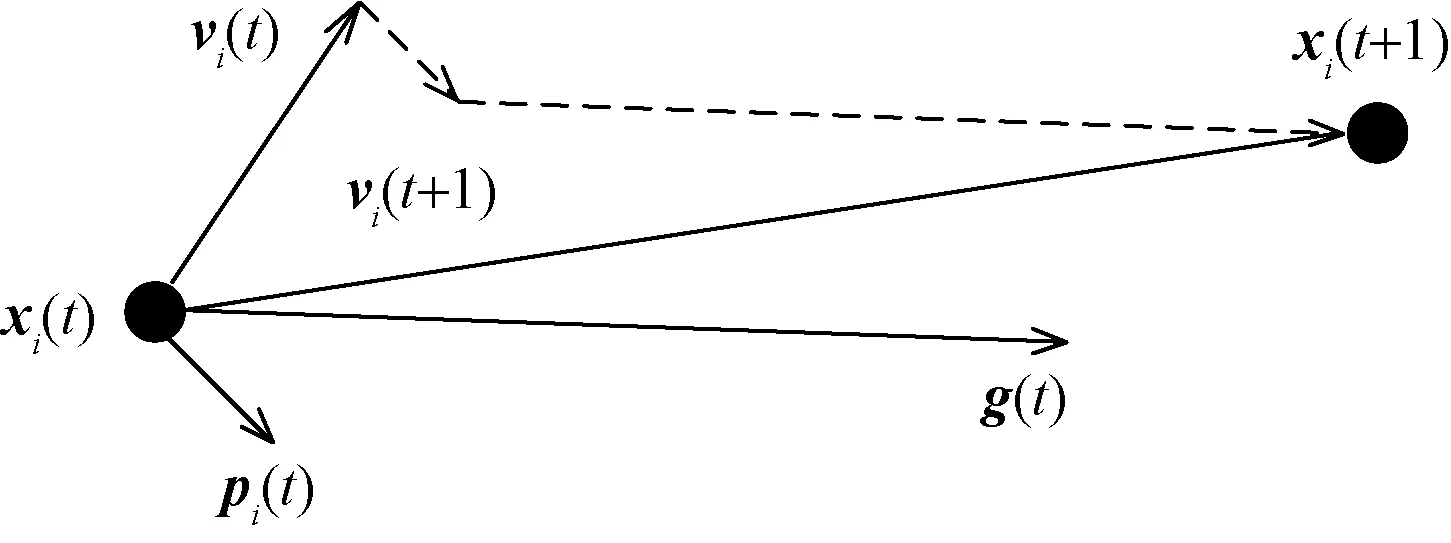
图3 粒子位置更新过程Fig.3 Particle position update process

如图3所示，t时刻下的第i个粒子拥有速度vi(t)和位置xi(t)这两个基本信息，以及个体最优位置pi(t)这一历史信息，并能通过与其他粒子交流获取当前全局最优位置g(t)的信息。然后粒子根据个体和全局最优位置不断改变速度的大小和方向，来更新自身位置。在N维空间内，粒子的各信息均以n维向量的形式存在，第i个粒子通过式(10)、式(11)更新自己在第n维的信息，可表示为

vin(t+1)=wvin(t)+c1r1[pin(t)-xin(t)]+c2r2[gn(t)-xin(t)]

(10)

xin(t+1)=xin(t)+vin(t+1)

(11)

式中：n为维度，n=1，2，…，N；xin为第i个粒子在第n维的位置；vin为第i个粒子在第n维的速度；gn为第n维全局最优位置；pin为第i个粒子在第n维的最优位置；w为惯性的权重因子，c1、c2为学习因子；r1、r2为[0,1]的随机数，称为种子数。其中惯性权重因子和学习因子的设置对算法性能有很大影响。

2.1.1 自适应权重

惯性权重因子对粒子群算法搜索最优解的能力有很大影响，惯性权重因子较大时，粒子群算法的全局搜索能力强，搜索速度快，但搜索结果精确度低；惯性权重因子较小时，粒子群算法的搜索结果精确度高，但搜索速度慢，且更容易陷入局部最优解。

自适应权重能够依据收敛程度和适应度值自动调整惯性权重因子大小，当适应度值小于平均适应度值时[14]有

(12)

当适应度值大于平均适应度值时有

w=wmax

(13)

式中:w为惯性权重因子；wmin为惯性权重因子的最小值；wmax为惯性权重因子的最大值；f为当前适应度值；favg为平均适应度值；fmin为最小适应度值。

自适应权重的加入使得算法能够更好地平衡全局与局部搜索的能力，提高了算法的性能。

2.1.2 自然选择

基本粒子群算法随迭代次数的增加，陷入局部最优解的可能也逐渐增大[15]。为解决这一问题，将源自遗传算法的自然选择机制引入粒子群算法。

自然选择发生在迭代过程的末尾，粒子每次更新位置后，将所有粒子按照适应度值排序，根据适应度值筛选出粒子群中1/2的粒子，用较好的1/2粒子的速度和位置替换较差的1/2粒子的速度和位置，并保留个体最优位置的信息。

自然选择的加入提高了粒子群算法对搜索区域信息的利用率，因此改善了搜索性能，降低了陷入局部最优解的可能。

2.2 轮胎侧偏力参数辨识

2.2.1 侧偏辨识目标函数

目标函数应使得辨识曲线与实验曲线之间的差值最小，轮胎参数辨识的目标函数为

(14)

式(14)中:xi为侧偏角；YPAC89(xi)为通过魔术公式计算得到的侧向力；YTest(xi)为通过实验得到的侧向力或回正力矩。通过算法寻优，使Z为最小值。

2.2.2 两级参数辨识

将改进的粒子群算法写入MATLAB，根据PAC89轮胎模型侧偏力魔术公式，将B、C、D、E、Sh、Sv作为一级参数，通过一级辨识得到，组成一级参数的a0～a13为二级参数，通过二级参数辨识得到。轮胎模型的侧偏力魔术公式参数辨识流程如图4所示。

图4中，先对3组实验进行一级辨识，然后综合三组实验的一级辨识的参数，进行二级辨识。二级辨识中，BCD需要根据式(3)进行计算，因此组成BCD的a3、a4、a5单独进行辨识，其他二级参数一同辨识。

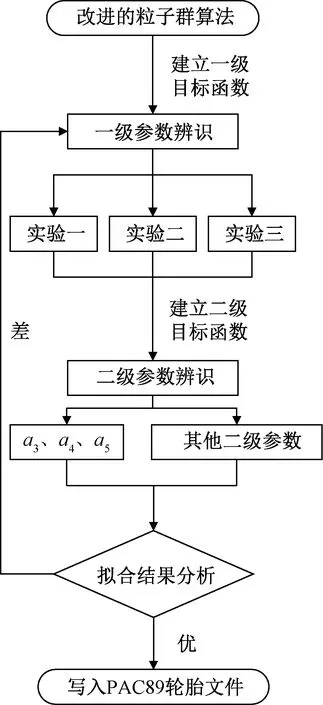
图4 参数辨识流程Fig.4 Parameter identification process

两级辨识中粒子群均采用相同的初始设置，其中粒子数目设置为1 000；两个学习因子均设置为2；最小惯性权值为0.4；最大惯性权重值为1；最大迭代次数为300。

3 辨识结果分析

3.1 一级辨识结果

一级辨识的目标函数单一且复杂，并分3组进行，3组均收敛才可以进行二级辨识，因此一级辨识对整个轮胎辨识工程中的辨识速度有较大影响。图5为3组实验一级辨识的迭代曲线，对6个一级参数的辨识中，实验一在38次迭代后收敛，实验二在35次迭代后收敛，实验三在迭代34次后收敛。说明轮胎参数的一级辨识速度很快。

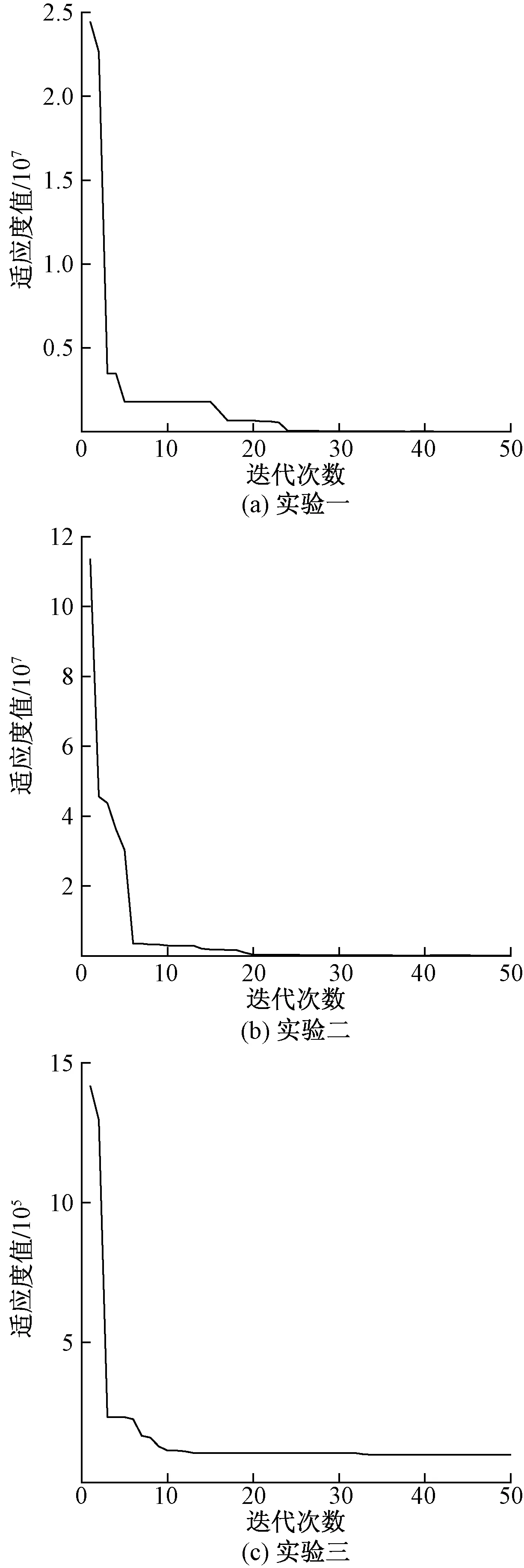
图5 一级辨识迭代曲线Fig.5 First order identification of iterative curve

一级辨识得到的参数辨识结果会作为二级辨识的基础数据被应用，因此一级辨识精度对二级辨识的收敛速度和最终轮胎模型精度有很大影响。为更好研究模型拟合效果，引入相对残差作为辨识精度评价指标[5]，其表达式为

(15)

式(15)中：G为相对残差；SSE为残差平方和；Ib为某点的实验数据；n′为各实验中实验测试点的总数。一级参数辨识结果如表2所示，辨识曲线如图6所示。

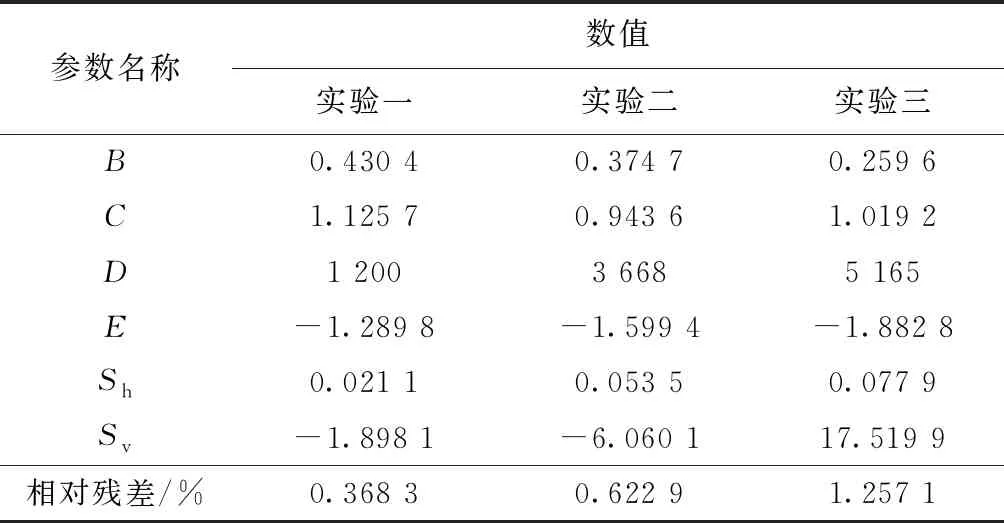
表2 一级参数辨识结果Table 2 First order parameter identification results

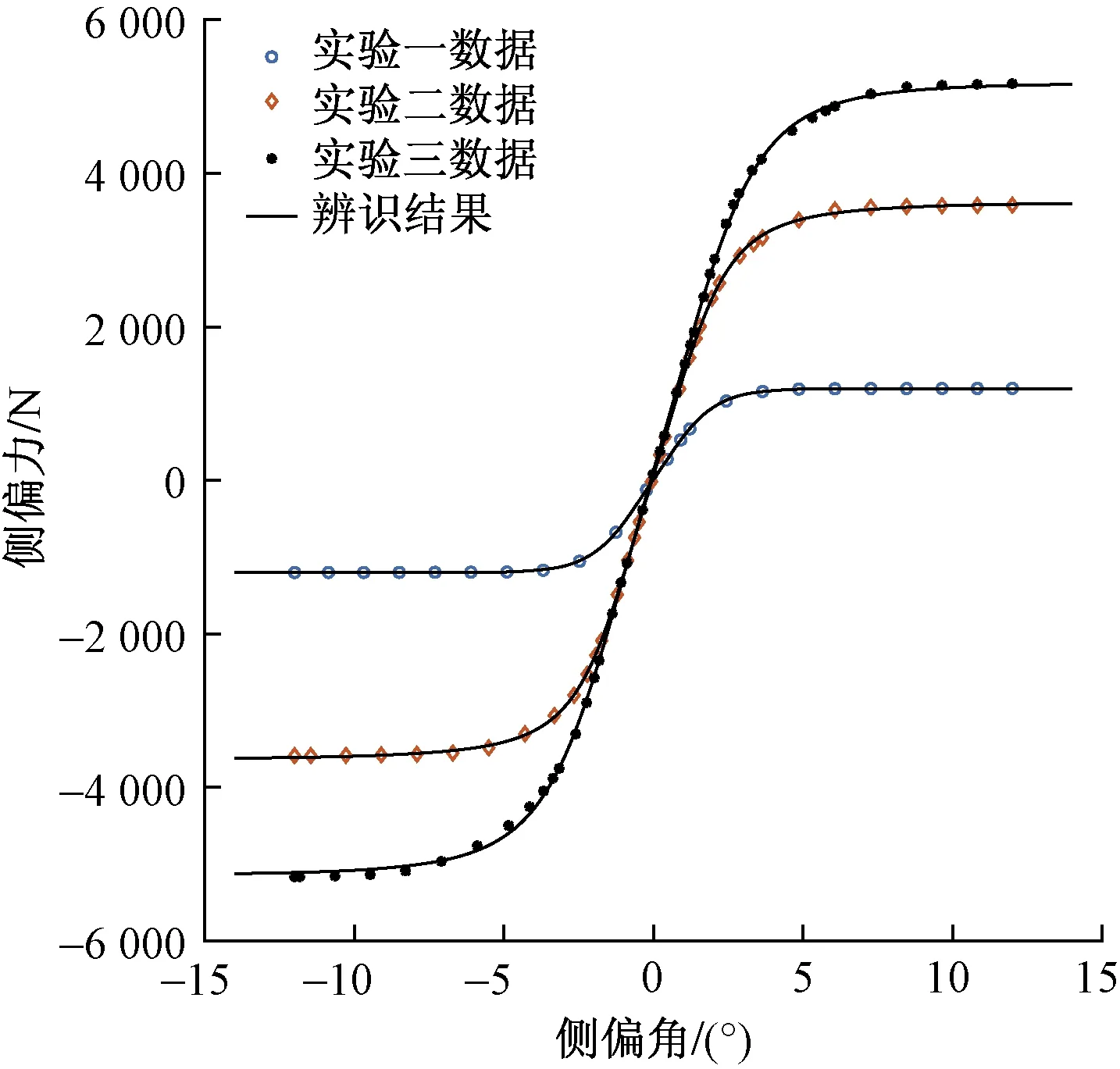
图6 一级辨识结果Fig.6 First order identification result

如图6所示，实验数据与辨识曲线吻合情况良好，辨识结果与3组实验的相对残差分别为0.368 3%、0.622 9%、1.257 1%，3组实验平均相对残差为0.749 4%，相对残差越小，说明辨识精度越高，轮胎一级辨识整体精度符合二级辨识的要求。

3.2 二级辨识结果

侧偏力二级辨识共辨识14个参数，这14个参数也是最终组成PAC89轮胎模型侧偏力部分的参数，因辨识参数较多，相较于一级辨识，收敛速度更慢，需要更长的辨识时间。图7为三组实验二级辨识的迭代曲线，其中a3、a4、a5在迭代10次左右便收敛，其他11个二级参数的辨识在迭代100次左右便收敛，迭代速度略慢于一级辨识。

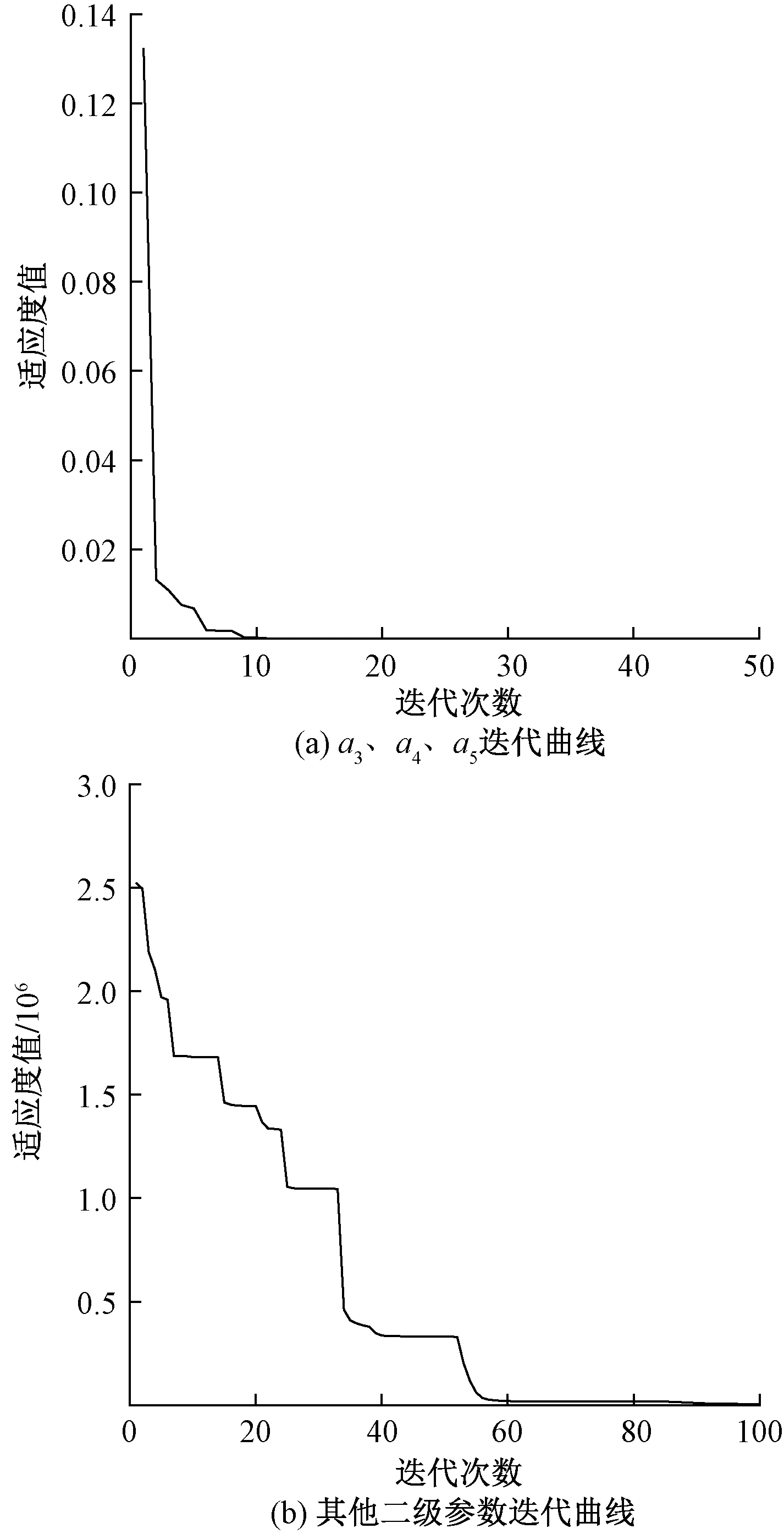
图7 二级辨识迭代曲线Fig.7 Second order identification of the iterative curve

二级辨识的参数作为最终的轮胎模型参数，其辨识精度便是PAC89轮胎模型的辨识精度。二级参数辨识结果如表3所示，辨识曲线如图8所示。

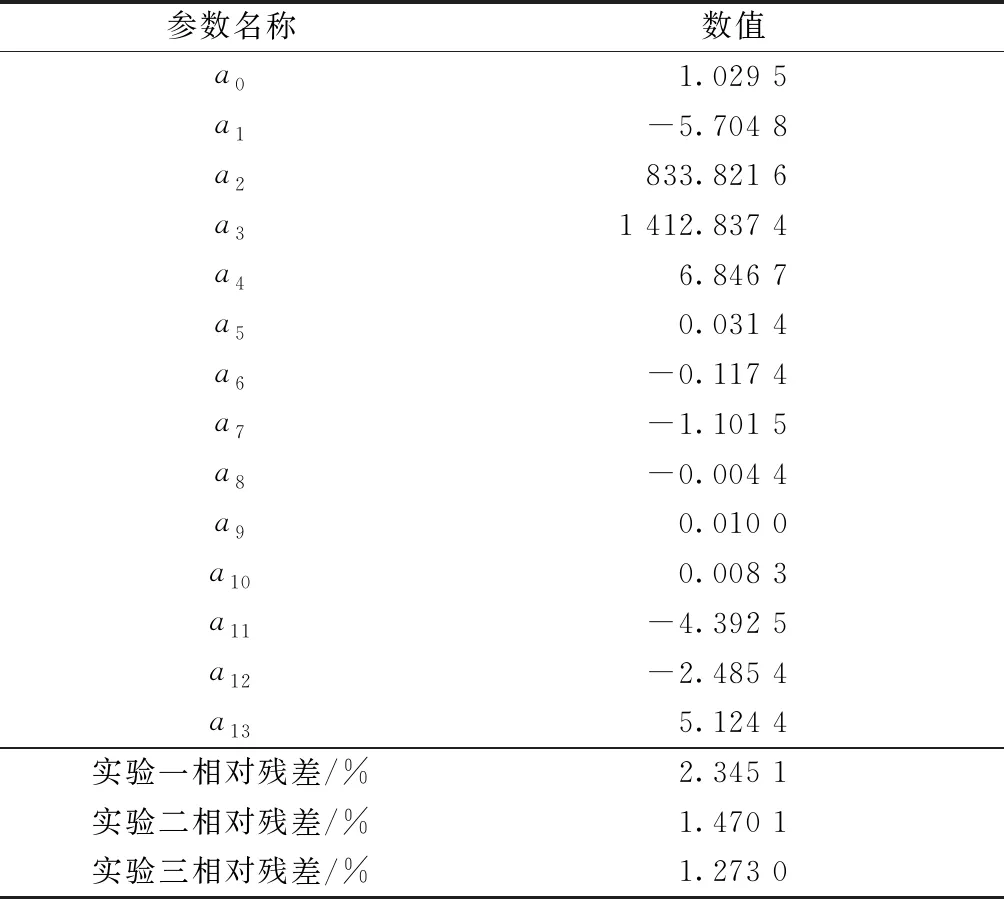
表3 二级参数辨识结果Table 3 Second order second order parameter identification results

如图8所示，实验数据与PAC89轮胎模型曲线的吻合情况良好，PAC89轮胎模型与实验数据的相对残差分别为2.345 1%、1.470 1%，1.273 0%，平均相对残差为1.696 1%，辨识精度高。

图8 二级辨识结果Fig.8 Second order identification result

4 结论

(1)改进粒子群算法结合参数分级，对PAC89轮胎模型进行了两级辨识。其中，一级辨识在迭代40次以内便收敛，且平均辨识精度为0.749 4%，辨识准确。与文献[5]相比，本文方法在所需辨识参数更多的情况下，有与文献[5]相当的辨识速度，以及更高的辨识精度。

(2)在对侧偏力的二级辨识中辨识了完整的14个特性参数，包括由于外倾角和帘线效应等原因造成的曲线水平和竖直偏移，因此二级辨识在迭代100次左右收敛，通过与三组实验数据比对，PAC89轮胎模型侧偏力曲线的平均辨识为1.696 1%。

(3)辨识结果表明，采用改进粒子群算法分两级进行辨识的方法能够快速、准确地得到PAC89轮胎模型的辨识结果，有利于缩短仿真研究周期并为智能轮胎研究中所需的实时参数辨识提供支持。