谐调螺栓连接对航空发动机静子系统动力学特性影响

姚星宇， 程 涵，2

(1.中国民用航空飞行学院航空工程学院， 广汉 618307； 2.中国空气动力研究与发展中心防除冰重点实验室， 绵阳 621000)

航空发动机是由静子系统、支承系统和转子系统组成的复杂机械结构[1]，静子系统和转子系统中存在大量不同连接形式的螺栓连接结构[2]。现代航空发动机转子高速、轻柔、重载的发展趋势使得螺栓连接结构对航空发动机转静子系统动力特性的影响越来越大[3-4]。因此，螺栓连接结构、载荷参数的选取将直接决定航空发动机的动力特性。

前人研究多集中在螺栓连接结构本身的性质上，如螺栓连接结构连接刚度特性[5]、蠕变寿命分析[6]和渐进损伤研究[7]等。但是关于螺栓连接载荷、结构参数及螺栓连接结构性能退化对航空发动机结构动力特性的影响的研究较少。

越来越多的研究人员意识到忽略螺栓连接结构研究航空发动机动力特性问题无论在试验上还是理论上都会出现较大的误差。研究表明，由连接对接面所产生的能量耗散可以高达机器总能量耗散的80%～90%，而材料本身所产生的能量耗散仅为总耗散能的10%～20%[8]。因此，随着有限元方法和计算机技术水平的不断发展，进行航空发动机动力特性研究时，需要考虑螺栓连接结构的影响。

为研究螺栓连接结构对航空发动机动力特性影响，需要对螺栓连接结构进行参数化建模。根据不同的需要，研究人员先后建立了精细有限元模型[2，9]、弹簧阻尼单元模型[8，10]、薄层单元模型[11-12]、改进薄层单元模型[13]。在这些模型中，精细有限元模型保留了结构所有的几何特征并充分考虑对接面的特性，能够研究外载荷、螺栓预紧力、止口紧度等参数对连接刚度的影响，但是该模型自由度数数目庞大，接触非线性会大大增加计算量和计算时间，因此很少在整体结构的动力学计算中使用。弹簧阻尼单元模型是常用模型之，一般使用刚度和阻尼系数来描述螺栓连接结构对接面的性质，能够考虑对接面所引起的阻尼和能量耗散问题，但是该模型将对接面的面-面接触问题简化为点-点接触，并且很难描述弹簧刚度、阻尼系数与螺栓的结构、载荷参数之间的关系，因此在航空发动机螺栓连接结构的建模中也存在局限性。薄层单元模型是在相邻对接面之间定义一层能够模拟接触力学特征的虚拟材料，以虚拟材料的力学性能参数来表征实际的界面接触刚度，它能够模拟复杂机械中的螺栓连接结构，并保持结构的完整性，且能够较准确地表征连接处的线性刚度特性，但是薄层单元参数的确定需要试验数据进行修正，且无法考虑航空发动机螺栓连接结构周向刚度分布不均的特点。改进薄层单元模型能够充分考虑航空发动机螺栓连接结构的周向非均匀刚度特性，并且基于螺栓对接面接触应力分布特点和分形基础理论，分块的薄层单元的材料参数可以通过螺栓连接的结构、载荷参数来确定，无需进行试验数据修正。

在设计阶段或航空发动机正常工作时，螺栓连接结构的每个螺栓沿着法兰边周向均匀分布，且预紧力相同，那么螺栓连接结构的连接刚度在整个法兰边周向是周期谐调分布的。根据上述研究的现状和不足，现将这种螺栓连接定义为谐调螺栓连接结构，利用改进薄层单元法对螺栓连接结构进行建模，研究航空发动机设计阶段或正常工作时，谐调的螺栓连接的载荷、结构参数对航空发动机静子系统动力特性的影响，为航空发动机螺栓连接结构的设计提供一定的指导意义。

1 螺栓连接结构改进薄层单元法的基本理论

图1为螺栓连接结构改进薄层单元法的基本原理示意图，连接区域的薄层单元分块，其中圆形区域代表螺栓的区域，剩下的区域代表法兰对接面的接触区域。

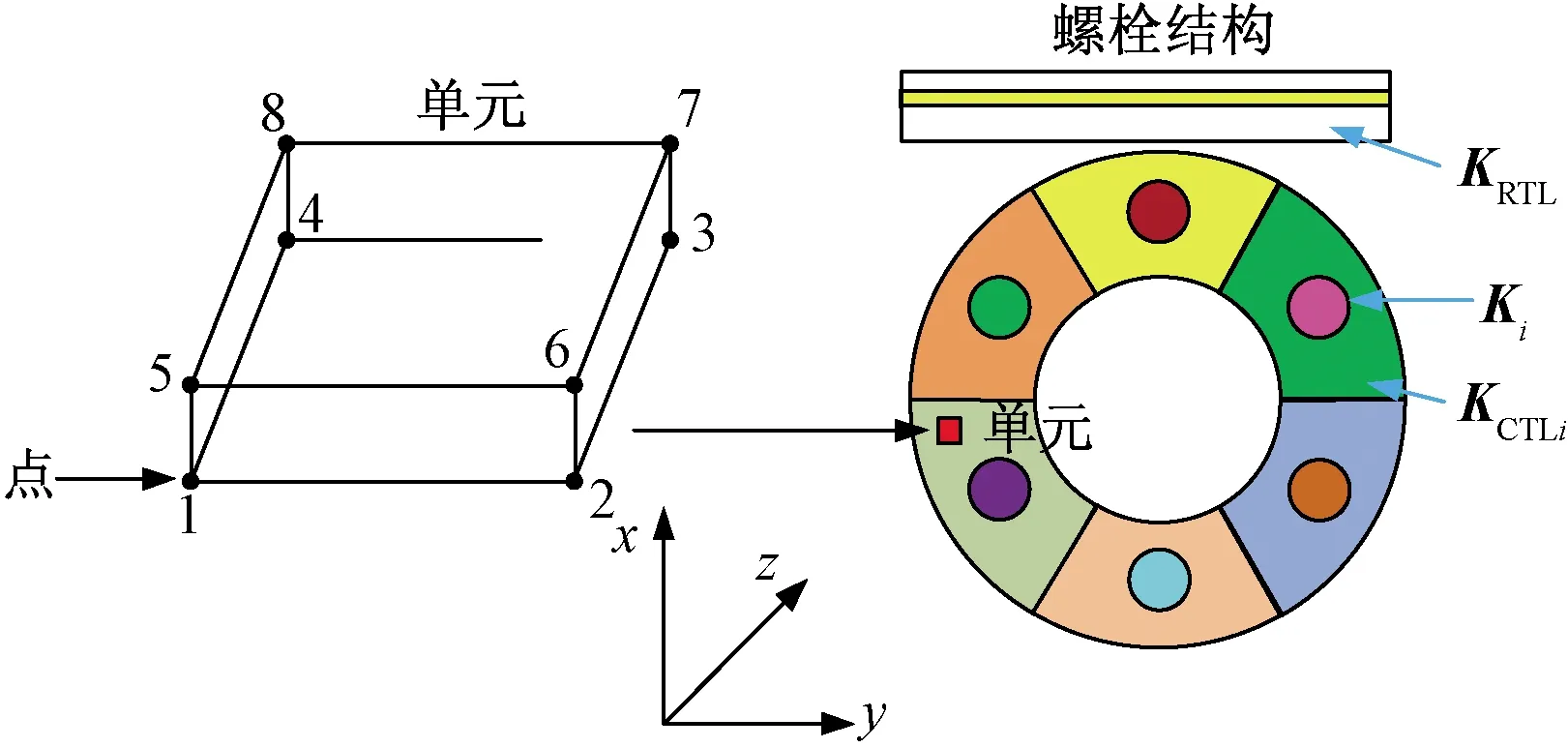
1～8为节点图1 螺栓连接结构的改进薄层单元法Fig.1 Improved thin-layer element method of bolted joint

分块的薄层单元为8节点六面体实体单元，单元中任一点位移(x,y,z)与节点坐标(xi,yi,zi)的关系可表示为

(1)

单元应变ε、单元应力σ与节点位移的关系为

ε=BaeT

(2)

σ=Dε=DBaeT

(3)

式中：Ni为形函数；B为单元几何矩阵；D为弹性矩阵；ae为某个单元中的节点位移向量。

根据虚功原理，单元刚度矩阵为

Ke=∮V0BTDBdV0

(4)

式(4)中：V0为单元的体积。

最后，单元刚度矩阵Ke与节点力向量Fe集合成整个结构的刚度矩阵K和节点力向量F，并考虑结构中的螺栓连接，得到结构静力学有限元方程为

(5)

动力学有限元方程为

(6)

对于薄层单元的材料属性，每个区域需要独立的力学参数弹性模量E、y向切变模量Gy、z向切变模量Gz来模拟3个不同方向的刚度[12]，并且每个区域的材料参数与其他区域的不同。因此，对整个螺栓连接结构，需要6N(N为螺栓数目)个材料参数来表征螺栓连接结构分块的薄层单元。此时，可以选择正交各向异性材料作为薄层单元的材料，通过相应的物理假设[13-14]，本构方程简化为

(7)

式(7)中：σx为x向正应力；σy为y向正应力；σz为z向的正应力；τxy为xy平面的剪切应力；τyz为yz平面的剪切应力；τxz为xz平面的剪切应力；c11为x方向的弹性模量；c44为xy平面的弹性模量；c55为yz平面的剪切模量；εx、εy、εz分别为x、y、z向的正应变；γxy、γyz、γzx分别为xy、yz、xz平面的剪切应变。

综上所述，从有限元方程形成和材料选取两方面阐述了改进薄层单元法的基本理论过程。

2 谐调螺栓连接对静子系统固有特性的影响

在航空发动机静子系统中，典型的螺栓连接结构几乎都具有法兰边，并且螺栓大多沿法兰边周向均布，数目众多。因此，航空发动机静子系统的螺栓连接结构可简化为由螺栓连接起来的短粗薄壁圆筒结构。选取两个完全相同的带法兰边的薄壁圆筒结构来模拟航空发动机的静子系统，然后两个薄壁圆筒通过12个M20的螺栓连接起来，如图2所示。圆筒部分和螺栓的材料属性相同，如表1所示，其中E、v、ρ分别为材料的弹性模量、泊松比和密度，Ra为接触面的粗糙度，σ0.2、H分别为较软材料的屈服强度和硬度。

根据姚星宇[15]所提出的改进薄层单元模型，将其应用到该机匣的螺栓连接结构中，研究螺栓连接结构的载荷、结构参数对系统固有特性的影响规律。

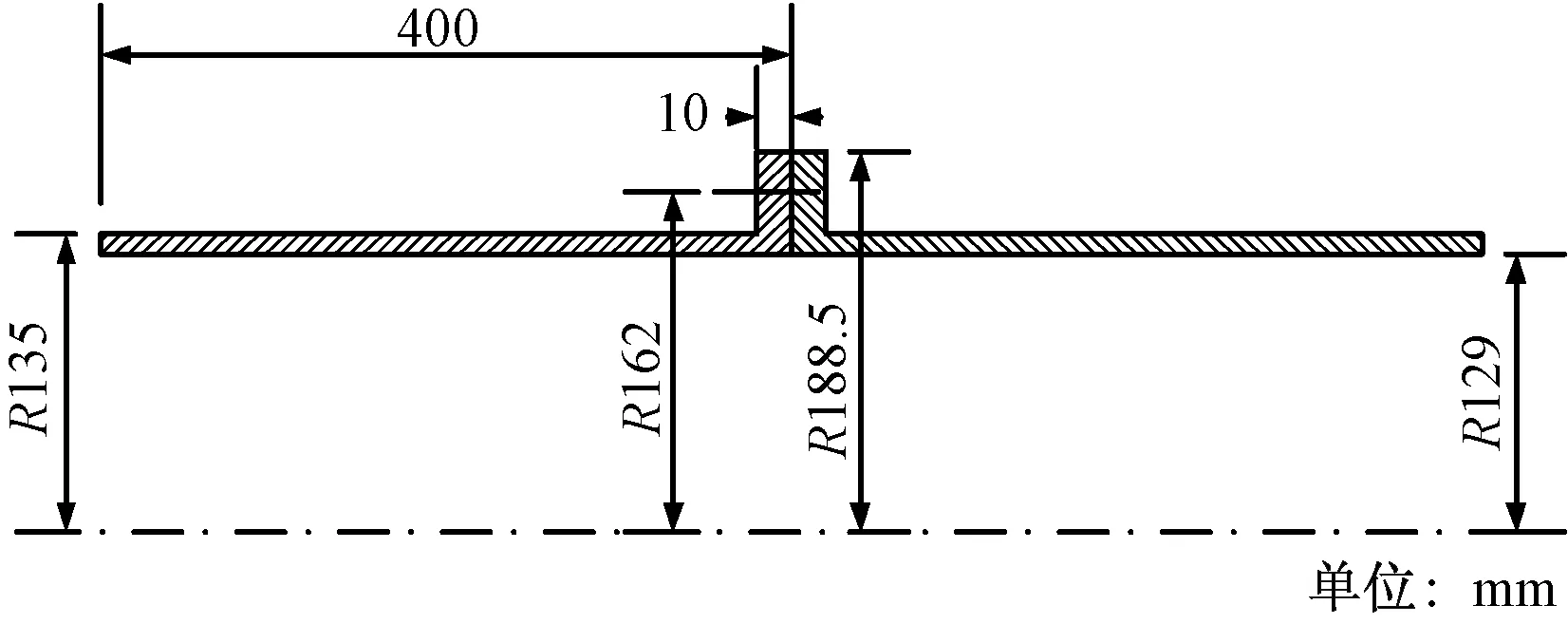
R为半径图2 机匣的螺栓连接结构Fig.2 Bolted joint structure of the casing

2.1 螺栓预紧力

根据改进薄层单元法的理论，得到不同预紧力条件下(每个螺栓分别为20、40、60、80、100 N·m)谐调螺栓连接处的相关数据，如表2所示，其中连接刚度kBJS为螺栓连接结构的连接刚度，根据文献[16]，航空发动机螺栓连接结构的连接刚度主要由螺杆区域和法兰边夹紧区域决定，如图3所示[16]，因此，法兰边厚度一致的双层螺栓连接结构的连接刚度kBJS可表示为

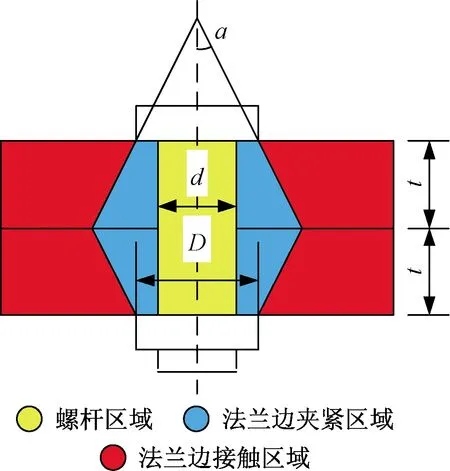
图3 双层法兰边螺栓连接结构的连接区域[16]Fig.3 Connection region of bolted joint structure of double members[16]

表2 不同预紧力下机匣螺栓连接处的数据Table 2 Parameters of bolt joints of the casing under different preload

(8)

式(8)中：db为螺杆直径；Eb为螺杆弹性模量；t为子法兰边的厚度；E1、E2为子法兰边的弹性模量；D为螺母压紧区域直径；d为螺孔直径；α为锥形半角。

(9)

定义刚度比k为

(10)

式(10)中：kRigid为刚性连接时该连接处的刚度，可表示为

(11)

图4为不同预紧力条件下刚度比(k)的变化曲线，可以看出：当预紧力在20～100 N·m变化时，k由16.51%增大到16.84%；在其他条件不变的情况下，增加每个螺栓的螺栓预紧力，螺栓连接处的刚度比缓慢增加，当螺栓预紧力增大到一定程度时，刚度便趋于稳定；k均小于17%，说明与刚性连接相比，该螺栓连接结构刚度损失达80%以上。

图4 不同预紧力下的刚度比Fig.4 Stiffness ratio under different preload

利用ANSYS的模态分析功能，对图2所示的结构进行建模和模态分析，得到了不同预紧力条件下该螺栓连接结构机匣的模态特性。螺栓连接部分的有限元模型如图5所示，提取该模型前6阶横向弯曲振动固有频率，如表3所示，相应的模态振型如图6所示，可以看出：随着螺栓预紧力的增加，机匣的前6阶横向弯曲振动固有频率均增加；螺栓预紧力对不同阶固有振动影响程度不同，对第1阶振动影响最大，对第2、4、5、6阶振动影响次之，对第3阶振动几乎没有影响，从而导致每阶固有频率的增加量也不同。比如，当螺栓预紧力从20 N·m增加到100 N·m时，第1阶振动从1 290.39 Hz增加到1 399.28 Hz，增加量为108.9 Hz，远大于第3阶振动的0.79 Hz(从3 535.78 Hz增加到3 536.41 Hz)；不同预紧力下，结构固有频率与刚性连接时结构固有频率相比均有下降，说明螺栓连接结构的连接刚度会影响整个机匣的刚度，局部刚度损失会影响整个结构动力学特性。

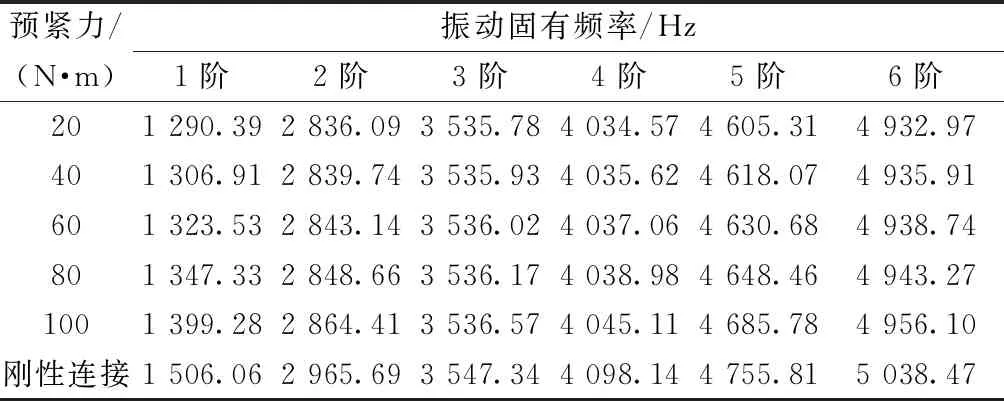
表3 不同预紧力条件下机匣的前6阶振动固有频率Table 3 The first 6 order vibration natural frequency of the casing under different preload

2.2 螺杆直径

当机匣系统的螺杆直径在16～24 mm变化时(此时预紧力为100 N·m)，螺栓连接处的相关数据如表4所示，看出：当螺杆直径增加时，锥形半角逐渐减小，但螺杆区域半径却因为螺杆直径的增大而增大；螺栓连接处的连接刚度随着螺栓直径的增加而增加；刚度比k在0.113 0～0.233 0变化。

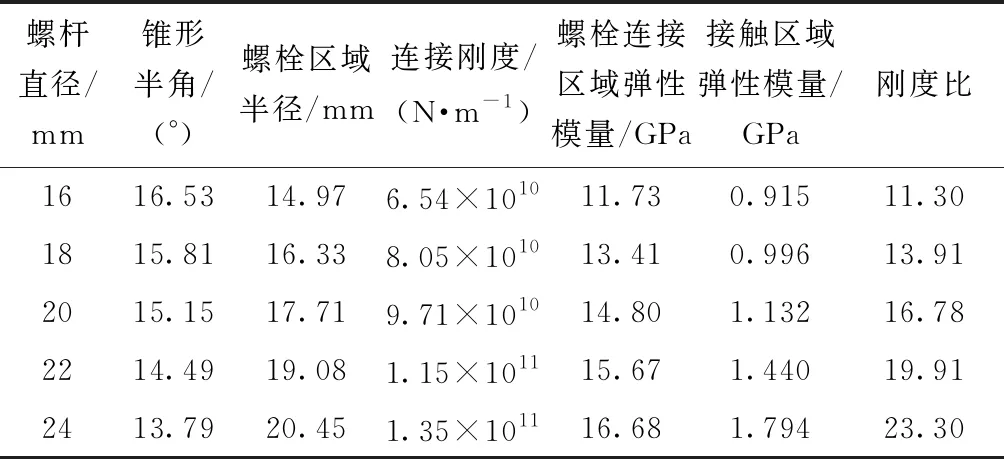
表4 不同螺杆直径条件下机匣螺栓连接处的相关数据Table 4 Parameters of bolt joints of the casing under different bolt diameters

不同螺杆直径条件下螺栓连接结构机匣的前6阶横向弯曲振动固有频率如表5所示，相应的模态振型与图5类似，在此不列出，从表5可以看出：随着螺杆直径的增加，机匣的前6阶横向弯曲振动固有频率值均增加；螺杆直径对不同阶固有振动的影响规律与螺栓预紧力类似，仍是对第1阶振动影响最大，对第2、4、5、6阶振动影响次之，对第3阶振动几乎没有影响，从而导致固有频率增加量不同。

图5 螺栓连接处的有限元模型Fig.5 Finite Elements of bolt joint structure

2.3 螺栓材料参数

当机匣系统的螺栓弹性模量在150～195 GPa变化时，螺栓连接处的相关数据如表6所示，可以看出：当螺栓弹性模量增大时，锥形半角逐渐增大，螺栓区域半径也逐渐增大；螺栓连接结构的连接刚度随着螺栓弹性模量的增大而增大。

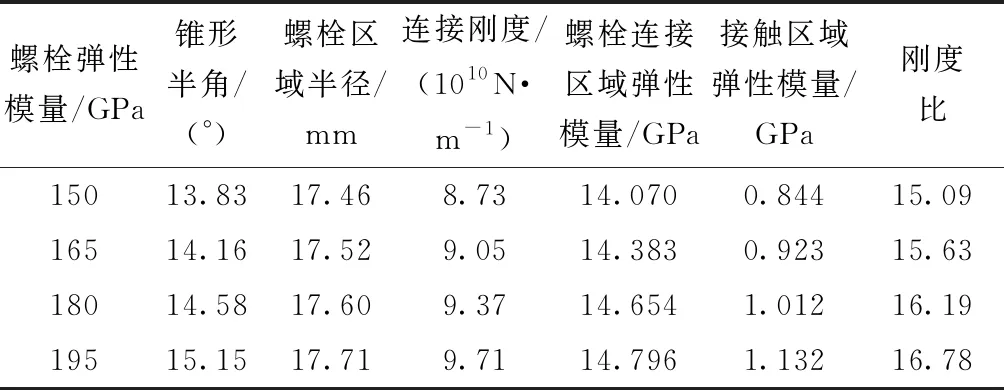
表6 不同螺栓材料参数条件下机匣螺栓 连接处的相关数据Table 6 Parameters of bolt joints of the casing under different bolt material parameters

不同螺栓材料参数条件下螺栓连接结构机匣的前6阶横向弯曲振动固有频率如表7所示，可以看出：随着螺栓材料弹性模量的增加，机匣的前6阶横向弯曲振动固有频率值均增加；螺栓弹性模量对每阶振动的影响程度与螺栓预紧力、螺杆直径类似。

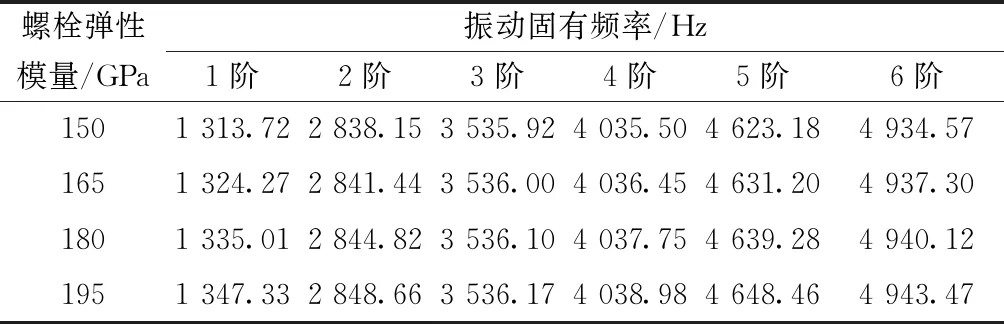
表7 不同螺栓材料参数条件下机匣的前6阶振动固有频率Table 7 The first six order vibration natural frequency of the casing under differentbolt material parameters

2.4 螺栓个数影响

当螺栓个数在6～14变化时，螺栓连接处的相关数据如表8所示，可以看出：当螺栓个数变化时，锥形半角、螺栓区域半径将不变，此时螺栓连接结构的连接刚度只与螺栓个数有关；当螺栓个数从6个增加到14个时，刚度比k由0.083 9增大到0.195 7；在其他条件不变的情况下，随着螺栓个数的增加，刚度比线性增加。

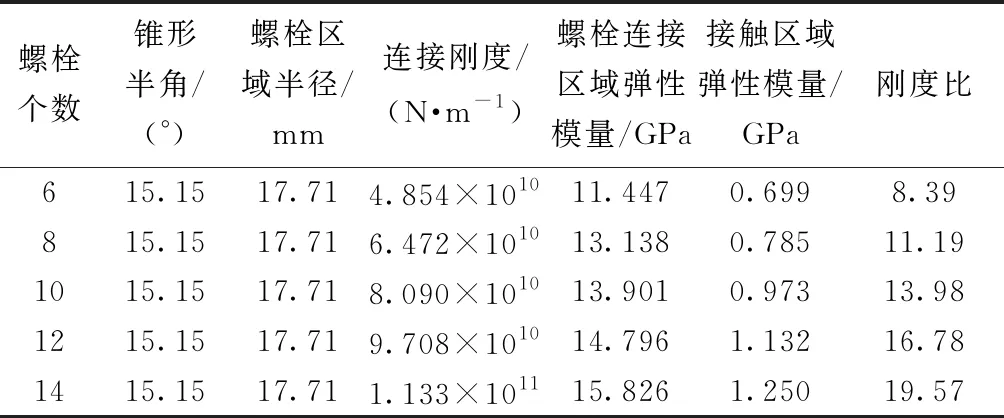
表8 不同螺栓个数条件下机匣螺栓连接处的相关数据Table 8 Parameters of bolt joints of the casing under different bolt numbers

不同螺栓个数条件下螺栓连接结构机匣前6阶横向弯曲振动固有频率如表9所示。从表9可以得出如下结论。

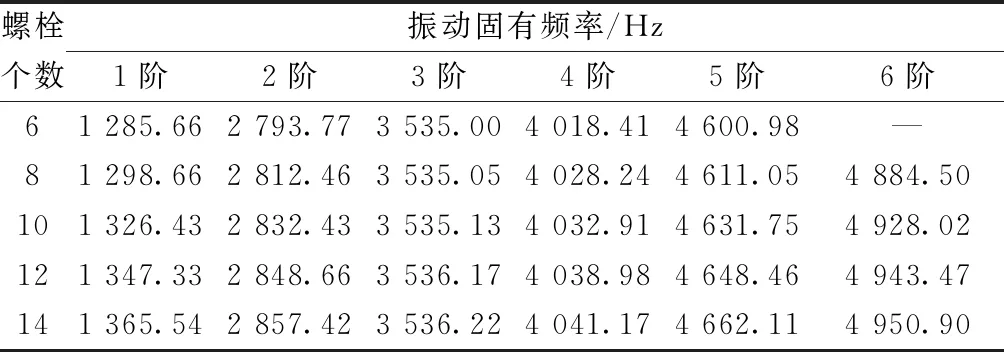
表9 不同螺栓个数条件下机匣的前6阶振动固有频率Table 9 The first 6 order vibration natural frequency of the casing under different bolt numbers

(1)随着螺栓个数的增加，机匣的前6阶横向弯曲振动固有频率值均增加。

(2)螺栓个数的减少会使机匣结构的某些振型消失或者模态置信度(MAC)下降，这是因为螺栓个数太少时，螺栓连接处的局部连接刚度与整个结构的刚度相差太大，螺栓连接处会出现局部振动所导致。

例如，当螺栓个数为6时，机匣的第6阶弯曲振动振型消失，第2阶横向弯曲振动的模态振型与其他螺栓个数机匣的同阶模态振型置信度下降，如图7所示，通过MAC计算，螺栓个数为6的结构的第2阶振型与螺栓个数为12的结构的第2阶振型的模态相似度为0.919，而螺栓个数为10的结构与其的模态相似度为0.999。

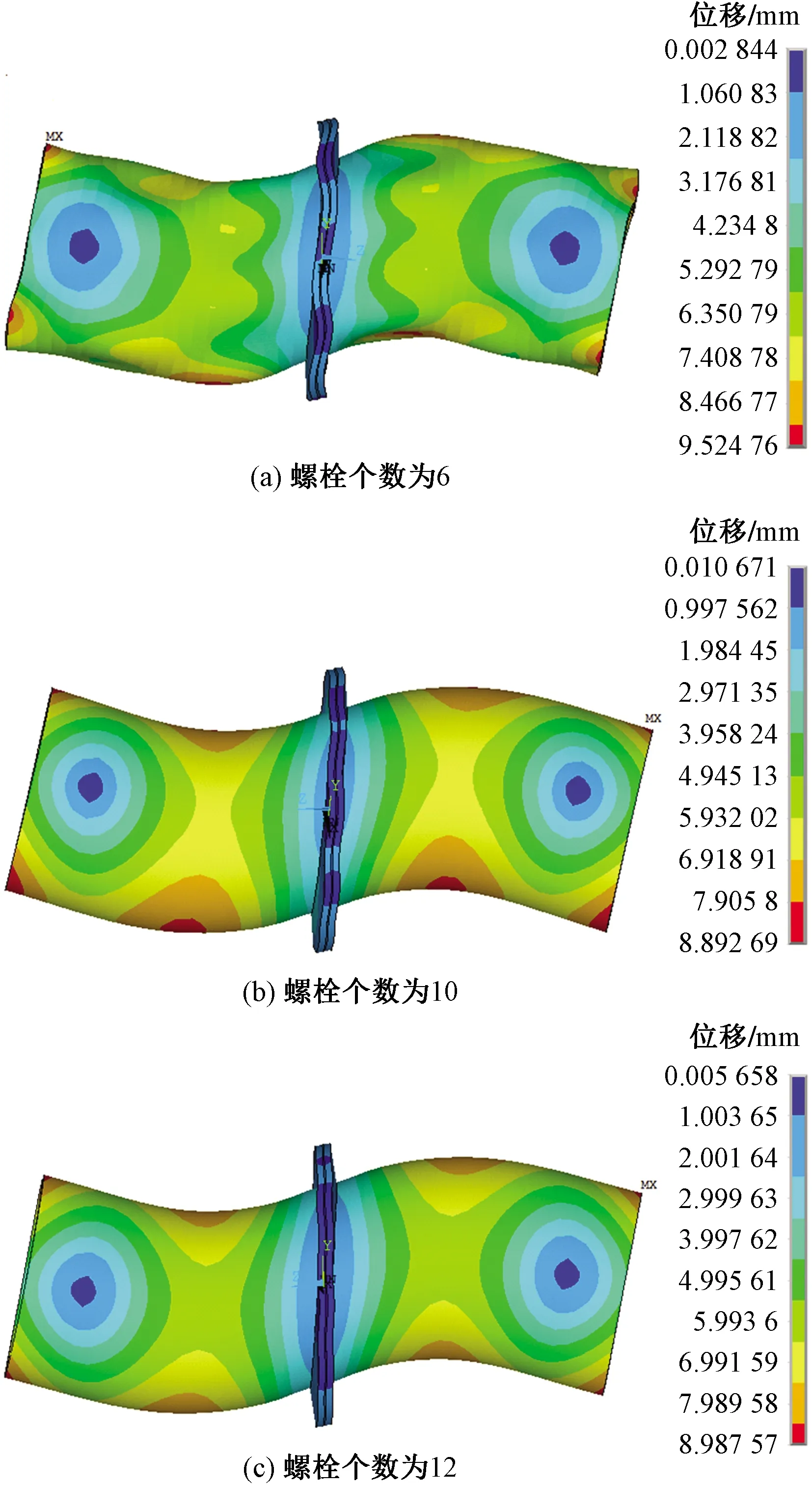
图7 不同螺栓个数条件下机匣的第2阶模态振型Fig.7 The second order vibration mode of the casing under different bolt numbers

(3)螺栓个数对每阶振动的影响程度与其他参数的规律有所不同，对第1、6阶振动影响最大，当螺栓个数从8个增加到14个时，第1阶振动增加量为66.88 Hz，第6阶振动增加量为66.4 Hz，第2、5阶振动的影响程度次之，螺栓个数对第3阶振动也几乎没影响。

2.5 小结

螺栓预紧力、螺杆直径、螺栓弹性模量、螺栓个数均对结构的固有特性有影响，但是影响的程度有差异，而且同一参数对结构不同阶振动的影响也有差异。定义参数χ来表征不同载荷、结构参数对螺栓连接结构机匣固有特性的影响程度，可表示为

(12)

式(12)中：Δω表示改变某个参数时机匣某阶振动固有频率的改变量；Δk表示某个参数改变时刚度比的改变量。

图8为不同参数对机匣各阶弯曲振动的影响程度，分别表示螺栓预紧力F、螺杆直径D、螺栓材料参数E和螺栓个数N。可得出如下结论。

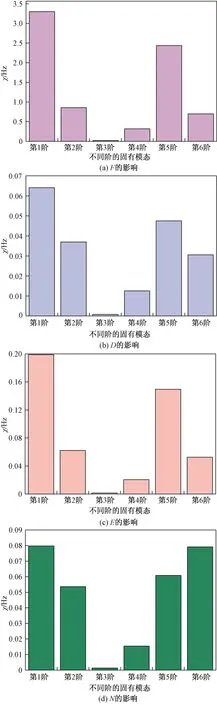
图8 不同参数对机匣各阶弯曲振动的影响Fig.8 Influence of different parameters on the bending vibration of the casing

(1)从整体上看，螺栓预紧力F对机匣各阶横向弯曲振动影响最大，参数χ分别为3.299 7、0.858 2、0.023 9、0.319 4、2.438 5、0.700 9 Hz，远大于螺杆直径D、弹性模量E、螺栓个数N对各阶横向弯曲振动的影响，排名第2的是螺栓材料参数E。

(2)具体到各阶横向弯曲振动，对第1、5阶振动的影响程度最大。如螺栓预紧力F对第1、5阶弯曲振动影响的参数χ分别为3.299 7 Hz和2.438 5 Hz，说明当螺栓预紧力的改变使螺栓连接结构连接刚度增大1%时，机匣结构的第1、5阶振动的固有频率将增加329.97 Hz和243.85 Hz。

(3)第3阶横向振动对所有参数的改变均不敏感，螺栓预紧力的参数χ仅为0.023 9 Hz，其他参数(螺杆直径D、螺栓材料参数E、螺栓个数N)甚至都小于0.002 Hz。这主要与该阶振动的振型有关，如图6所示，在第1阶弯曲振动中，螺栓连接处的弯曲振动较大，所以该连接处的连接刚度对整个结构的影响较大，而其它阶的振动，螺栓连接处的弯曲振动要弱很多，所以影响要小很多。

综上所述，对机匣结构固有特性影响最大的参数是螺栓预紧力，其次是螺栓弹性模量；具体到机匣结构的各阶振动，不同的参数对第1、5阶横向弯曲振动影响最大，而对第3阶振动几乎没有影响。因此，在航空发动机静子系统螺栓连接结构的设计阶段，需要特别注意螺栓预紧力的选取；在航空发动机运行阶段，需要时刻监测螺栓连接结构的预紧状况。

3 谐调螺栓连接对静子系统稳态响应特性的影响

由第2节的分析可知，螺栓预紧力对航空发动机静子系统的固有特性影响最大，而且在航空发动机运行期间，螺栓连接结构中只有预紧力会发生变化。因此，本节将着重讨论螺栓预紧力对航空发动机静子系统稳态响应特性的影响规律。

3.1 分析模型

仍以第2节的机匣系统作为研究对象，螺栓连接处用改进薄层单元法来建模，薄层单元厚度为2 mm，相关参数如表2所示，机匣的有限元模型及边界条件如图9所示，其中横向方向为y向和x向，轴向方向为z向。机匣的一端固定，在另一端部的y向节点处施加y向载荷，载荷大小为100 N，施加方式如图10所示，应用模态叠加法计算结构的稳态响应，计算范围为0～1 500 Hz，计算载荷步为750步，结构阻尼系数为0.000 2。分析模型包括刚性连接时的结构以及螺栓预紧力分别为100、80、60、40、20 N·m的结构。

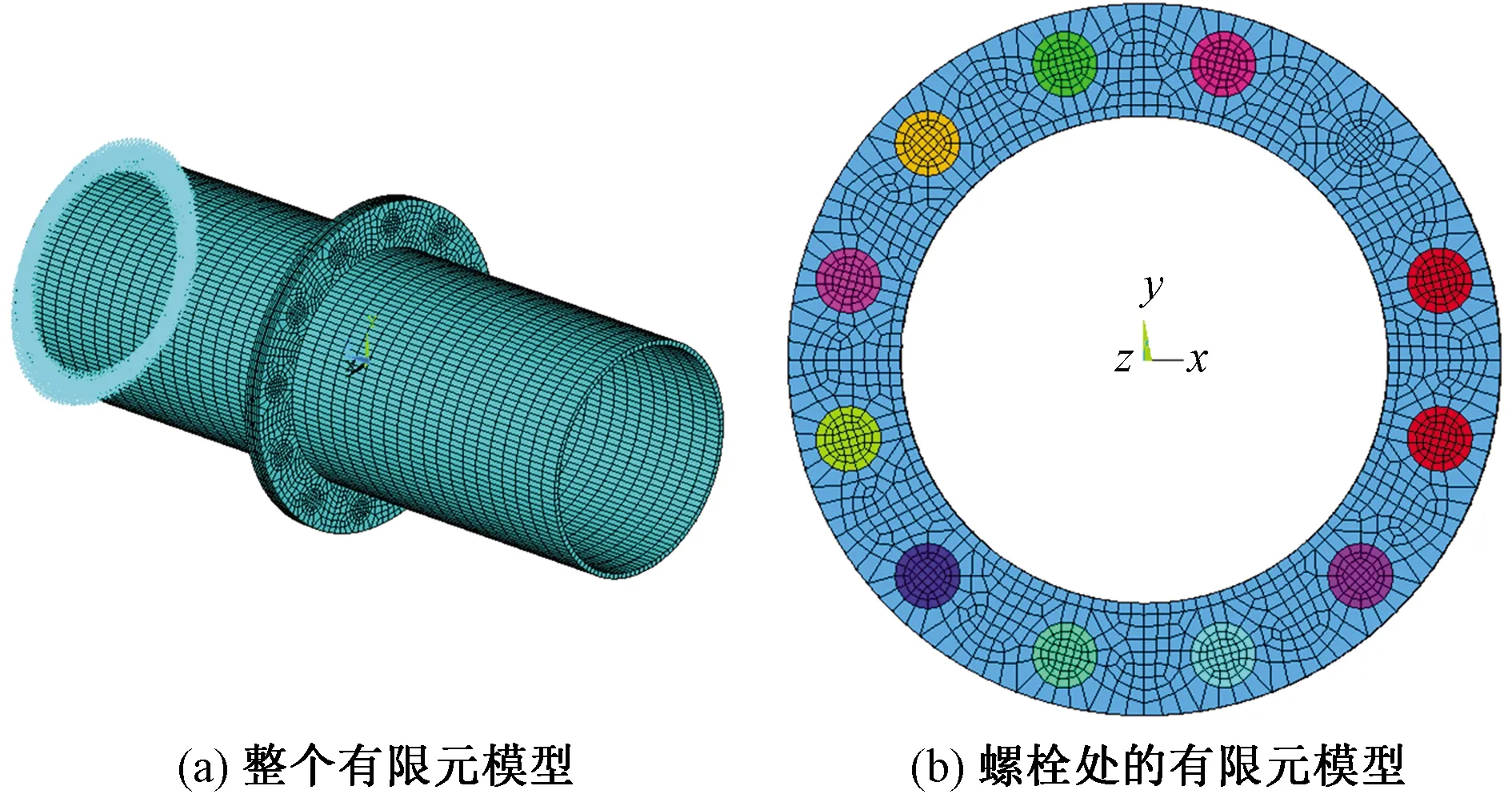
图9 机匣系统的有限元模型和边界条件Fig.9 Finite model andboundary condition of the casing

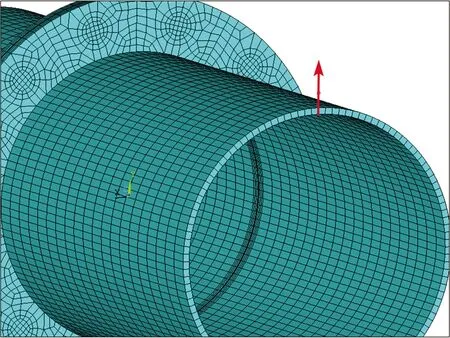
图10 机匣系统的载荷施加形式Fig.10 Form of load application of the casing

3.2 结果分析

提取加载点的Y向和Z向(轴向)的稳态响应幅值，其响应曲线分别如图11、图12所示，可得出如下结论。

图11 机匣加载点Y向响应曲线Fig.11 Y-direction response curve at loading point of the casing

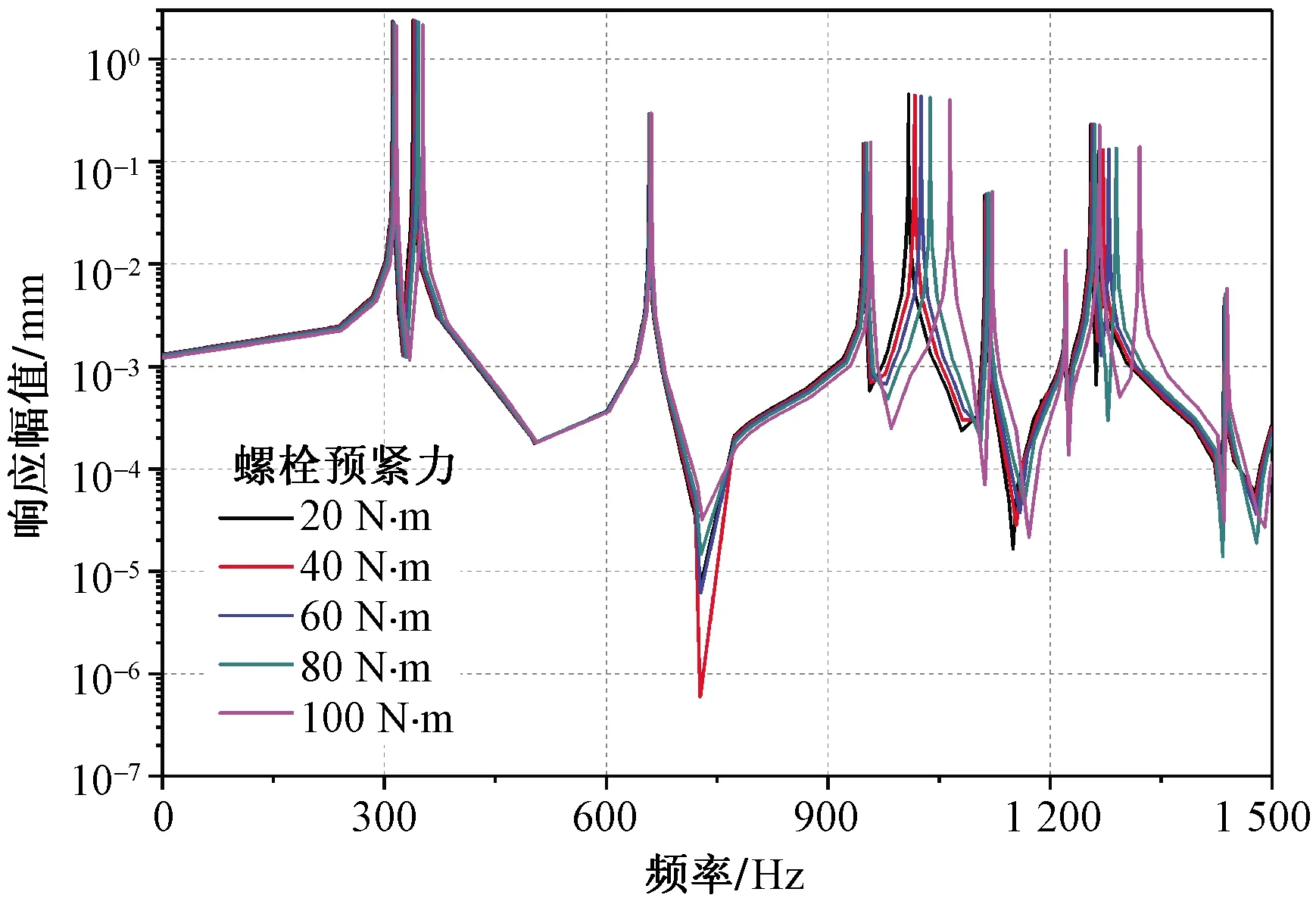
图12 机匣加载点Z向响应曲线Fig.12 Z-direction response curve at loading point of the casing

(1)刚性连接结构的峰值点所对应的频率值大于螺栓连接结构同阶峰值点所对应的频率，如向响应曲线的第5个峰值点(图11)，刚性连接结构的频率为1 121.4 Hz，预紧力20 N·m结构的频率值为1 008.5 Hz，差值为112.9 Hz，因此对于航空发动机的静子系统，不能忽略螺栓连接结构的影响。

(2)随着螺栓预紧力的降低，响应曲线的同阶峰值点逐渐向左移动，这是因为螺栓预紧力的降低使得螺栓连接处的连接刚度降低，从而使得整个结构的刚度降低，如Y向响应曲线的第5个峰值点，随着螺栓预紧力的降低，峰值点所对应的频率分别为1 064.7、1 038、1 025.7、1 017.1、1 008.5 Hz，所对应的振型如图13(b)所示。

(3)同阶峰值点的幅值随着螺栓预紧力的降低逐渐升高，这也是连接刚度降低的原因。如Y向响应曲线的最大峰值点(图11)，预紧力100 N·m的峰值为30.948 7 mm，预紧力20 N·m的峰值为33.820 2 mm，增幅为9.3%。

(4)不同峰值所对应的振型对螺栓预紧力的敏感程度不同，如Y向响应曲线的第4、5个峰值点，随着螺栓预紧力的降低，差值分别为3.1 Hz和56.2 Hz，分别对应的振型如图13所示，可知结构整体弯曲振型对螺栓预紧力的敏感程度要大于结构局部的波振型。

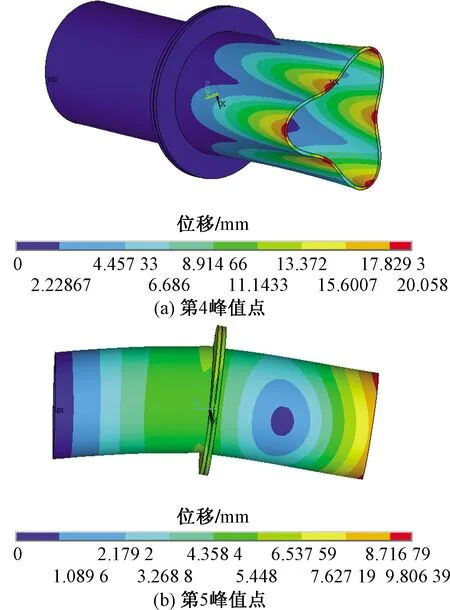
图13 机匣系统第4、5个峰值点所对应的振型Fig.13 Vibration modes of the fourth and fifth peak point of the casing

(5)谐调螺栓连接结构机匣系统受到Y向载荷作用时，加载点的Z向位移几乎为零，说明谐调螺栓连接结构的连接刚度是对称的；加载点会产生轴向位移，这主要是受到Y向载荷所产生的弯矩作用，但轴向位移远小于Y向位移。

4 结论

首先提出了谐调螺栓连接结构的概念，然后将改进薄层单元法应用到航空发动机静子机匣的谐调螺栓连接结构中，研究了螺栓连接的载荷、结构参数对静子机匣系统固有特性的影响，并提出了刚度比k和参数χ来说明影响的规律，最后研究了螺栓预紧力对机匣稳态响应特性的影响。得出如下结论。

(1)对于连接刚度周向均匀分布、预紧力相同的螺栓连接结构叫谐调螺栓连接结构。

(2)螺栓预紧力对机匣固有特性影响最大，当螺栓预紧力的改变使螺栓连接结构连接刚度增大1%时，机匣结构的第1阶固有频率将增加329.97 Hz。

(3)所有参数均对第1阶横向弯曲振动影响最大，对第3阶振动几乎没影响，这与不同阶振动的振型有关。

(4)随着预紧力的降低，稳态响应曲线的同阶峰值点向左移动，且幅值越来越高，这是连接刚度下降的原因。

(5)不同峰值对应的振型对螺栓预紧力的敏感程度不同，结构整体弯曲振型对螺栓预紧力的敏感成都要大于结构局部的波振型。