榫连接结构叶片盘振动特性研究及验证

龙 伦， 张红晓， 成晓鸣， 陈光炯

(中国航发湖南动力机械研究所结构强度研究部， 株洲 412002)

榫连接结构是航空发动机中一种常见的连接结构[1]，多见于压气机叶片盘、涡轮叶片盘等零件上。由于榫连接结构叶片盘工作在高离心、高压的载荷环境下，承受较大的稳态应力，为了避免出现高周疲劳破坏，给榫连接结构叶片盘的振动设计提出巨大的挑战。目前科研人员在榫连接叶片盘振动设计方面开展了大量的研究工作。李世林等[2]、王春洁等[3]、魏武国等[4-5]采用ANSYS软件使用循环分析方法对压气机叶片盘进行了含预应力下的振动特性计算分析。张原等[6]、吴佳等[7]、杨修伟等[8]对涡轮叶片盘进行了盘-片耦合振动特性分析，并结合Campbell图评估了叶片盘振动设计的合理性。但这些文献为了建模方便均将叶片与轮盘之间的榫连接结构一体化处理，这与不同工作状态下因榫接触面紧度不同造成的榫连接刚度不同的实际情况不一致，因此这种建模方式可能带来一定的计算误差。

首先基于静强度分析获得榫连接接触面的当量应力与变形，采用刚度等效的方法将榫连接接触面刚度等效为节点刚度，其次在叶片盘建模时通过ANSYS软件中的matrix27单元模拟该连接刚度，再次依据建立的模型开展了考虑榫连接刚度的叶片盘预应力下的盘-片耦合振动分析，最后借助动应力试验对计算结果进行验证。

1 榫连接结构等效刚度研究

由于工作状态下榫连接结构的接触状态处于高度非线性，而振动分析只能进行线性求解，因此不能直接在用于振动分析的叶片盘有限元模型中建立标准接触对，以模拟榫连接结构的接触状态。

1.1 等效刚度计算方法

为了获得榫齿接触刚度，可对考虑接触关系的叶片盘进行强度分析，在结果中提取每个接触面各节点的当量应力和总变形量，计算出每个接触面平均等效当量应力σ和平均总变形量l，根据平均等效当量应力σ乘以接触面面积S再除以该接触面节点数N，可求得接触面每个节点的等效接触刚度，即节点法向刚度可表示为

(1)

为了模拟轮盘对叶片轴向、切向的限制作用，给接触面各节点施加切向刚度单元。为探究切向刚度Kf的合理取值，对叶片盘多次进行振动分析，改变切向刚度的值，使其从104N/m逐渐增大到1010N/m，当Kf增加到108N/m后对叶片的振动特性无影响。所以切向刚度一般取108N/m左右，此时可以保证叶片榫齿在接触面的切向上不会发生滑移。

1.2 等效刚度施加

为了在有限元模型中简单方便的施加1.1节中获得所的节点等效刚度，采用ANSYS软件中提供的matrix27单元[9]对等效刚度进行模拟，其对称的上三角矩阵单元的系数如图1所示。

图1 matrix27矩阵单元系数Fig.1 Coefficient of matrix27 element

图1中，矩阵IUX、IUY、IUZ、IRX、IRY、IRZ、JUX、JUY、JUZ、JRX、JRY、JRZ表示节点I和J的6个方向的自由度，C1、C58、C7表示单元X方向的刚度，C13、C64、C19表示单元Y方向的刚度，C24、C69、C30表示单元Z方向的刚度。故榫连接结构等效刚度可通过在matrix27矩阵单元中输入式(2)的数值进行模拟。

(2)

2 考虑榫连接刚度的某型燃气涡轮叶片盘振动特性分析

2.1 网格划分及静强度分析

从涡轮叶片盘上切取包含一个完整叶片的1/41扇形区域，为提高接触分析的求解精度和收敛效率，对轮盘和叶片部分划分较为稀疏的网格，榫连接结构中榫头榫槽部分采用映射分网方式以保证榫接触面两者网格节点的一致性，方便后期建立matrix27单元，如图2所示。

图2 叶片盘网格模型Fig.2 Grid model of blade disk

在模型上施加各状态对应转速、温度、气动载荷；在轮盘安装面施加轴向和周向约束，在循环对称面上施加循环对称约束；在6对榫头榫槽配合面采用contact174和target170单元建立6对接触对，摩擦类型标准摩擦接触。

考虑到绘制叶片盘Campbell图的需要，进行两个状态的叶片盘频率分析，由于在0 r/min时无法计算接触刚度，故选取低转速10 000 r/min和设计转速45 000 r/min两个状态进行静强度分析。两种状态叶片榫结构处的应力分布如图3所示。

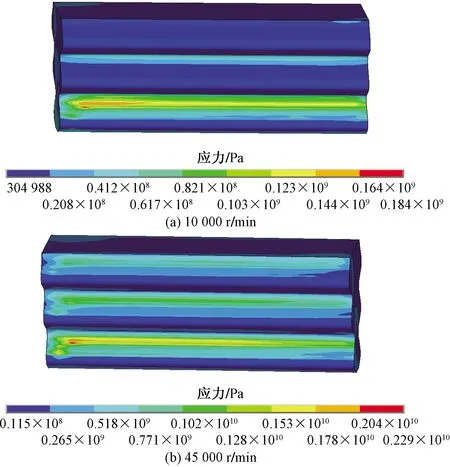
图3 叶片盘榫连接处静强度计算结果Fig.3 Static strength calculation results of tenon connection of blade disk

2.2 考虑榫连接刚度的叶片盘建模

根据等效刚度计算方法，提取榫连接接触面节点的当量应力和变形，如表1所示，根据式(1)，计算出各转速下各榫连接接触面节点法向等效刚度，结果如表2所示。在榫齿接触面对应节点处采用matrix27单元对两种状态等效接触刚度进行施加，构建用于振动分析的涡轮叶片盘模型，如图4所示。

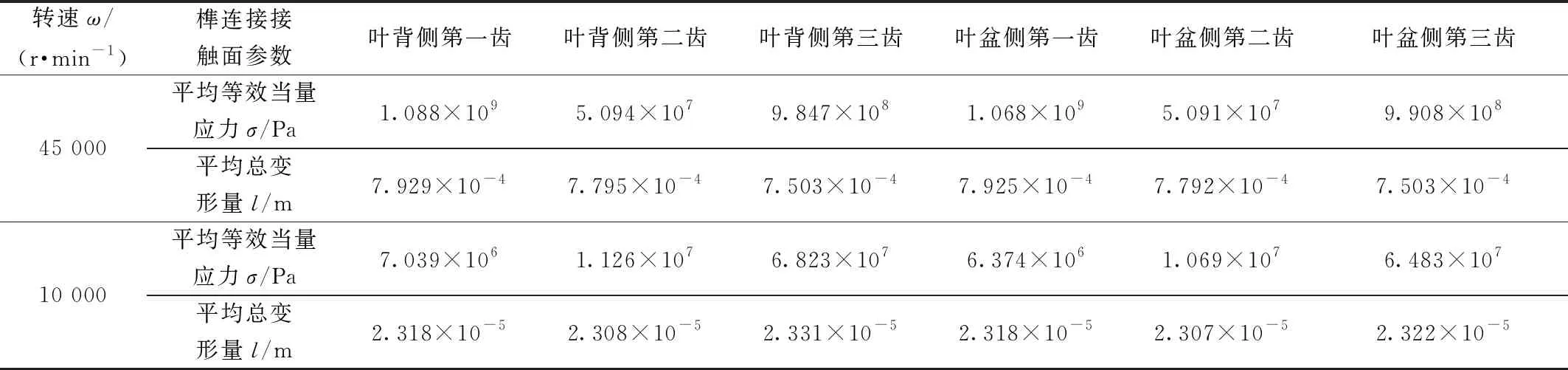
表1 榫连接接触面当量应力和变形量Table 1 Equivalent stress and deformation of tenon connection contact surface

表2 榫连接接触面节点法向等效刚度Table 2 Normal equivalent stiffness of tenon connection contact surface

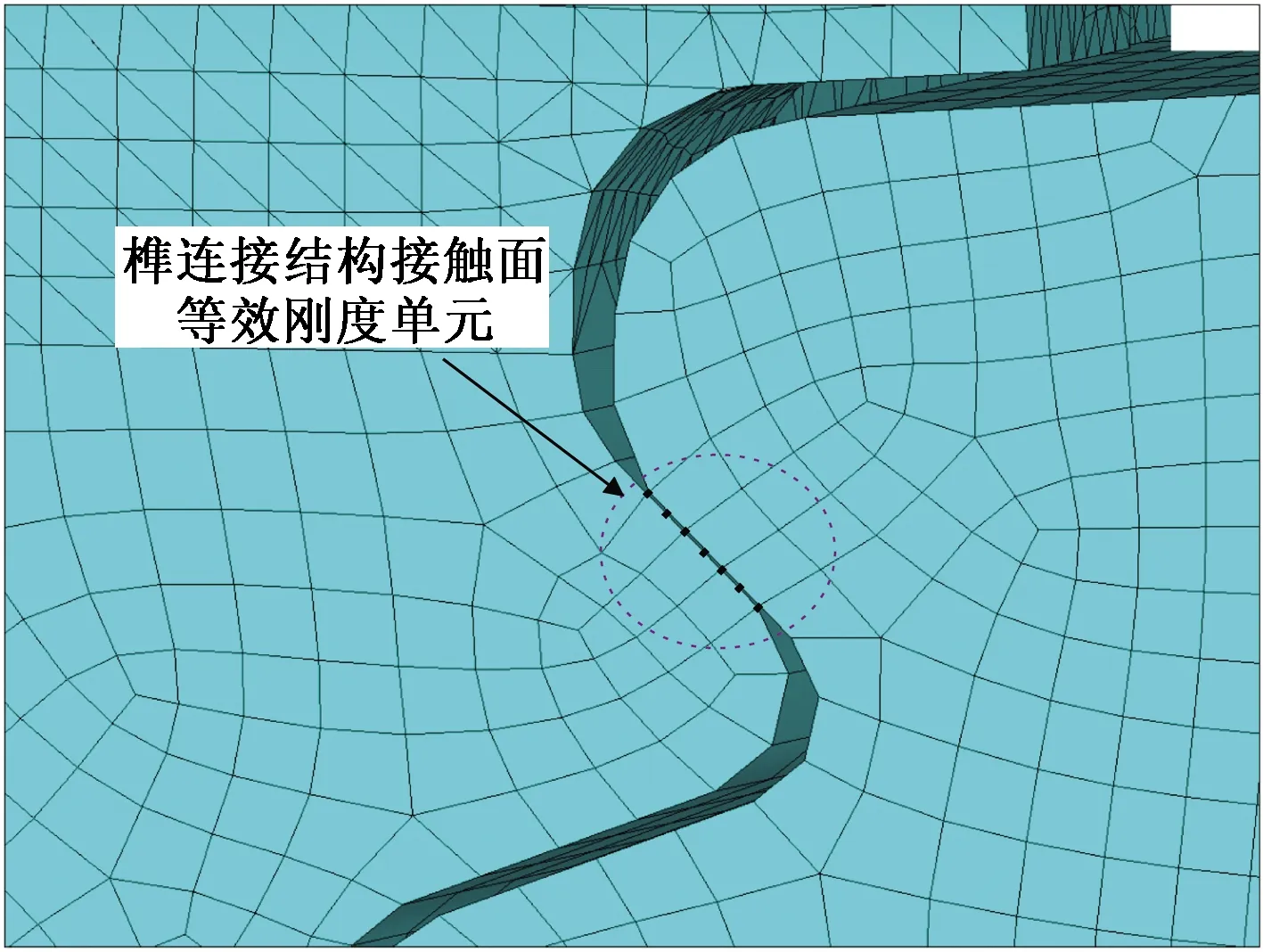
图4 考虑榫连接刚度的叶片盘模型Fig.4 Blade disk model considering tenon connection stiffness

2.3 振动特性对比分析

根据建立的两个转速下的考虑榫连接刚度下的叶片盘模型(模型1)-进行预应力下的盘-片耦合振动分析，其与榫连接结构一体化叶片盘模型(模型2)计算频率对比如图5所示。由图5可知：相同转速下，模型1计算得到的叶片各阶次频率均小于模型2计算得到的对应叶片频率；10 000 r/min转速下，叶片盘的各节径下的1阶频率差异较大，但2阶频率差异较小；45 000 r/min转速下，叶片盘的各节径下的1、2阶频率差异均较小；模型1和模型2计算得到的对应阶次叶片盘频率之间的差异随节径数变化不明显。

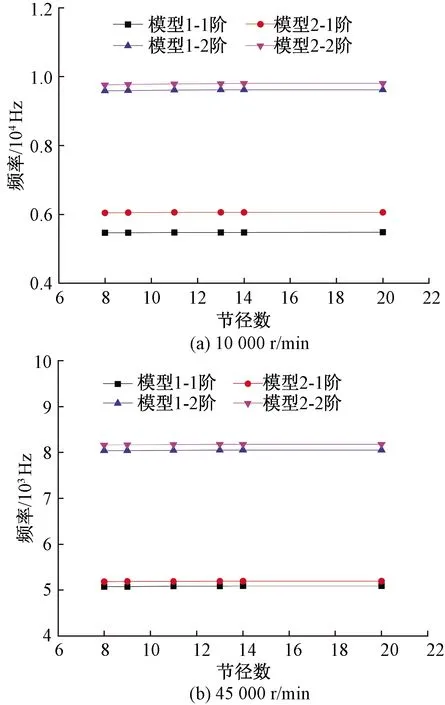
图5 不同转速下不同模型的频率对比Fig.5 Frequency comparison of different models at different speed

3 试验验证

为验证分析方法的精度，对该燃气涡轮叶片盘进行了动应力测试[10]，根据Campbell图对叶片盘各激振倍频下的共振转速进行了计算，实测的共振转速与两种叶片模型计算得到的共振转速对比结果如表3所示，可以看出：通过模型1计算得到的叶片盘共振转速与测试共振转速差异在6%以内；通过模型2计算得到的叶片盘共振转速与测试共振转速差异11%以内；模型1计算得到的叶片盘共振转速要小于测试共振转速；测试共振转速要小于模型2计算得到的叶片盘共振转速；由于叶片的1、2阶振型为叶片弯曲和扭转振型[图6(a)、图6(b)]，受榫连接结构处的刚度影响较大，因此随着激振倍频数的增加，通过模型1计算得到的叶片盘1、2阶共振转速与测试共振转速差异越来越小；由于叶片的3阶振型为叶片局部振型[图6(c)]，受榫连接结构处的刚度影响较小，因此通过模型1和模型2计算得到的叶片盘3阶共振转速与测试共振转速差异基本相当。

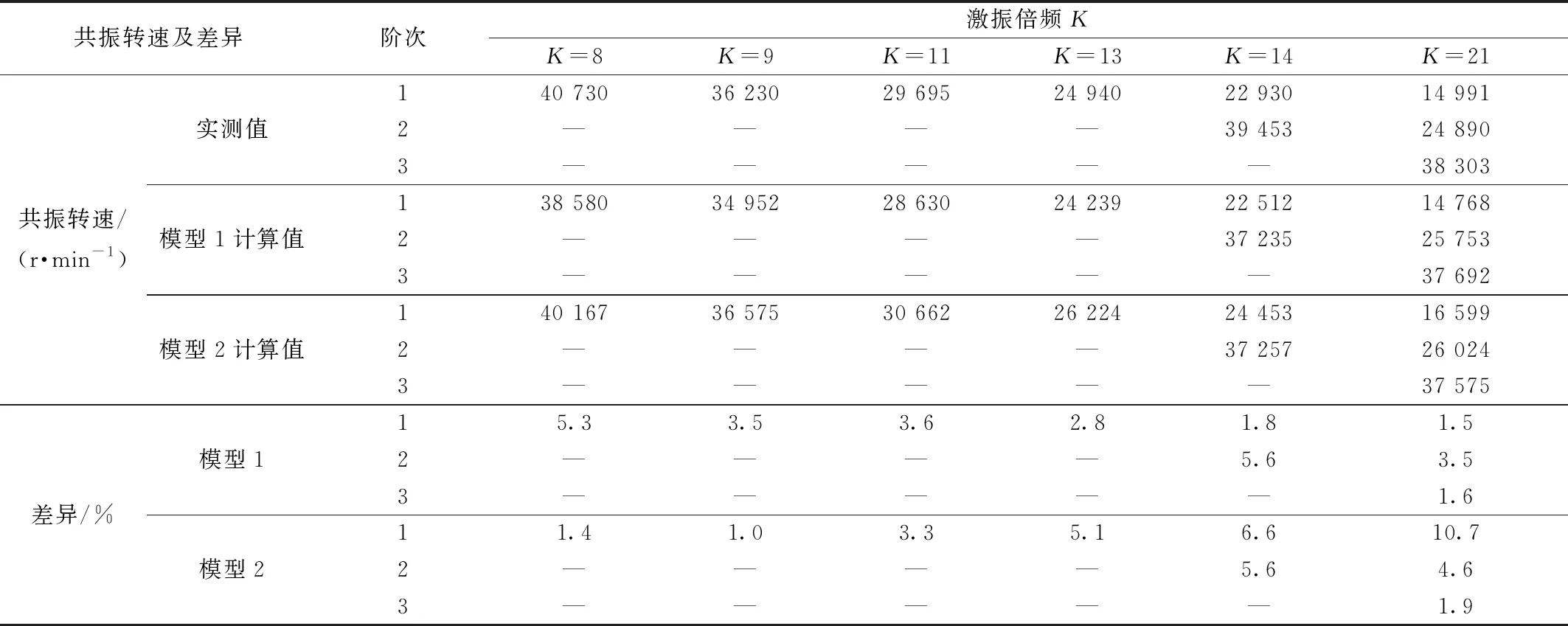
表3 实测与计算共振转速对比Table 3 Comparison of calculation and measurement of resonance speed

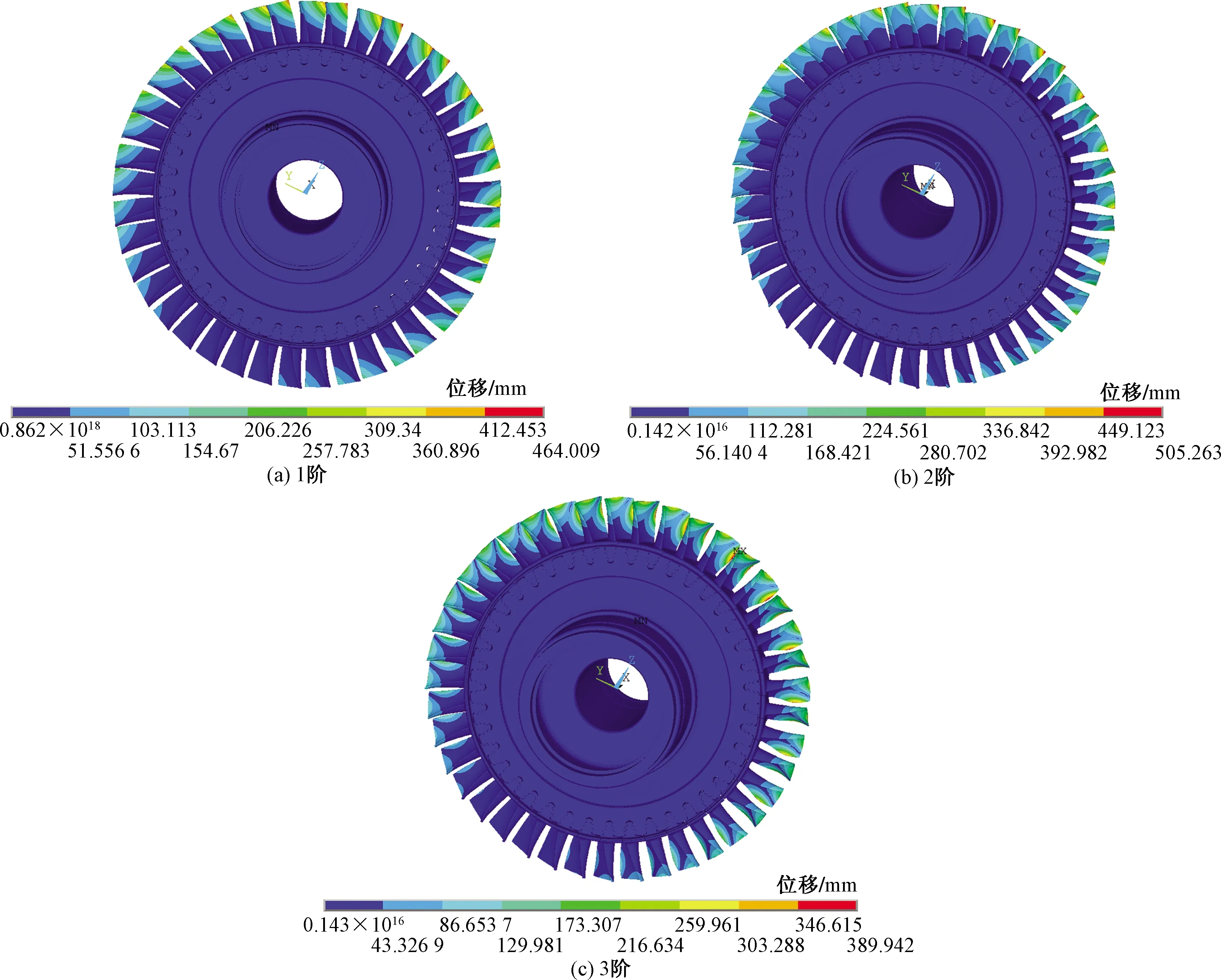
图6 叶片盘1、2、3阶振型Fig.6 1，2，3 mode shapes of blade disk

4 结论

通过开展考虑榫连接刚度下的叶片盘振动分析以及动应力测试试验，得到如下主要结论。

(1)采用考虑榫连接刚度的叶片盘模型分析得到的叶片盘共振转速计算精度在6%以内，可以满足工程设计要求。

(2)实测叶片盘共振转速介于考虑榫连接刚度的叶片盘模型分析得到的叶片盘共振转速与榫连接结构一体的叶片盘模型分析得到的叶片盘共振转速之间。

(3)榫连接结构处理方式对叶片盘1、2阶频率影响较大，对叶片盘高阶频率影响较小。