煤岩力学非均质性对孔渗性质的影响规律
刘雄飞, 郭建设, 汪道兵, 董永存, 李秀辉, 宇 波
(1.中国石油大学(北京)非常规油气科学技术研究院, 北京 102249; 2.东北石油大学石油工程学院, 大庆 163318; 3.中国石油吐哈油田分公司, 哈密 838202; 4.北京石油化工学院机械工程学院, 北京 102617; 5.北京石油化工学院, 深水油气管线关键技术与装备北京市重点实验室, 北京 102617)
煤岩是由有机物质和无机矿物质混合组成的复杂不均匀介质,具有很强的非均质性[1-2]。煤层气开采时渗透率和孔隙度受温度场、流动压力和岩石变形三者共同影响作用,地下煤岩的渗透率和孔隙度变化过程本质上为非均质岩体内热流固耦合过程[3-4]。CT扫描实验表明煤岩内部发育大量割理与裂隙[1,5-8],此特征使得煤岩存在强宏观力学非均质性,因此传统的均匀连续性假设与地下真实情况不相符,建立在传统均质假设基础上的孔隙度与渗透率时空演化分析方法受到严重挑战,这成为目前煤层气开采过程中亟待解决的关键力学问题。
煤层气开采过程中,受甲烷热传导、解吸和吸附的综合作用,煤岩温度发生变化[9-12]。实验证明,甲烷解吸过程中煤岩温度下降5 ℃左右[5-10]。因此,温度引起的热应力作用使得煤岩变形,从而将影响煤岩渗透率和孔隙度变化。在数值模拟方面,杨天鸿等[12]建立了考虑甲烷气体解吸、吸附作用的气体渗流—应力耦合作用模型,模拟结果表明:围压对瓦斯抽放效果影响较大,高围压下,若没有卸压作用,渗流阻力较大,瓦斯开采效果较差,但是该模型未考虑温度效应对煤岩渗透性的影响。侯永强等[6]建立了高温高压井筒耦合传热数学模型,应用有限差分法对该数学模型进行求解,通过数值模拟,得到了井筒及其腔体内流体的耦合传热过程温度场变化规律,该模型可为模拟井筒加温过程提供理论依据。王俊等[8]通过多场耦合数值模拟,分别研究泄漏压力、环境温度和障碍物等因素对埋地管道泄漏扩散的影响规律,结果表明,甲烷浓度随时间的变化曲线主要分为3个阶段:孕育阶段、快速增长阶段和缓慢增长阶段。马忠[13]考虑了瓦斯抽采期间的温度效应,建立了煤岩热流固耦合模型,结果表明提高温度可以促进大量吸附的瓦斯解吸,同时解析作用使得煤岩变形,有利于增加煤岩渗透率和孔隙度,但是该模型未考虑煤岩力学非均质性对煤岩孔渗参数的影响。在热流固模型基础上,魏晨慧[10]建立了热流固损伤耦合模型,研究了不同侧压系数和孔壁增温条件下煤岩的地应力变化和损伤演化过程,但是本模型为二维模拟。室内实验研究表明,煤岩渗透率与围压、温度和气压密切相关,煤岩渗透率一般随温度的升高呈递减趋势,但也有呈现先减小后增大趋势可能,因为煤岩渗透率变化是热膨胀、解吸和裂隙残余水分蒸发三者耦合作用结果[1-4]。但是,煤岩孔渗测试实验结果存在着较强的尺寸效应,即煤岩试样样品尺寸不同,孔渗测试实验结果也不同。
基于Weibull随机分布函数表征煤岩力学非均质性,建立了考虑煤岩甲烷吸附、解吸、煤岩变形、温度效应和气体压力相互耦合的渗透率与孔隙度时空演化三维有限元模型,通过Petrov-Galerkin有限元离散,分析了非均质度煤岩井筒附近孔渗参数的变化规律。研究结果对指导煤层气高效开采具有重要理论意义。
1 控制方程
研究涉及3个物理过程,即煤岩变形、甲烷气体渗流和传热过程,这3个过程之间是相互耦合的。各物理场控制方程如下。
1.1 岩石应力平衡方程
根据弹性力学理论,煤岩变形时满足的力学平衡方程为[11]
σij,j+Fi=0
(1)
式(1)中:σij为总应力张量, MPa;σij,j表示σij对第j个分量的偏导数;Fi为体积力向量, MPa。
根据Terzaghi有效应力理论,总应力场可分解为岩石骨架承受的有效应力场和孔隙内流体压力场,即
σij,j=σ′ij,j+αPδij
(2)
式(2)中:σ′ij为有效应力张量, MPa;σ′ij,j表示σ′ij对第j个分量的偏导数, MPa;α为Biot孔隙弹性常数,取值为0~1的小数;P为孔隙压力, MPa;δij为Kronecker符号。
煤岩变形时的总应变除了弹性应变外,还包括甲烷气体压力引起的应变、煤岩颗粒吸附甲烷所引起的线性吸附膨胀应变和热膨胀应变。因此,有效应力张量可表达为[12]
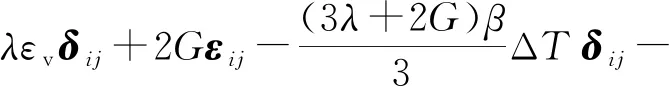
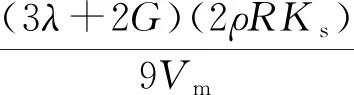
(3)
式(3)中:λ、G为拉梅常数, MPa;εv为岩石体积应变,小数;β为热膨胀系数, K-1;a、b为Langmuir吸附常数,单位分别为m3/kg和 MPa-1;Ks为煤岩颗粒体积模量, MPa;Vm为气体摩尔体积,L/mol;ρ为煤岩密度,kg/m3;T为温度,K;R为摩尔气体常数,J/(mol·K);Δ为拉普拉斯算子;εij为应变张量。
煤岩变形时几何方程为[3,13-16]
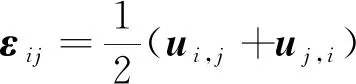
(4)
式(4)中:u为岩石位移向量,m。
联立式(1)~式(4)可得煤岩变形的力学平衡方程为[12-18]
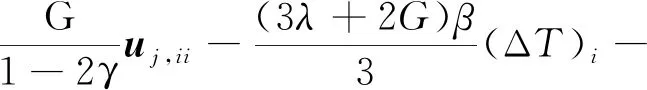
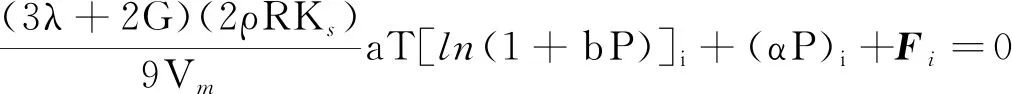
(5)
式(5)中:γ为泊松比;Pi为对压力x、y、z方向的偏导数。
1.2 渗流场控制方程
根据质量守恒定律、达西定律和Langmuir吸附方程,可得煤岩内甲烷气体满足的渗流场方程为[4,6,15-19]
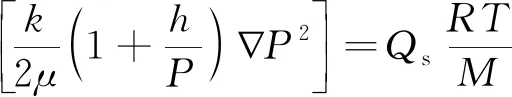
(6)
式(6)中:φ为煤岩孔隙度;t为时间,s;k为煤岩渗透率,m2;μ为气体黏度,mPa·s;M为气体分子量,g/mol;h为Klinkenberg系数,Pa;c为校正系数,kg/m3;Qs为源汇项,kg/(m3·s)。
1.3 温度场控制方程
根据傅里叶定律和能量守恒方程,可得温度场控制方程为[9-11]

(7)
式(7)中:η为煤岩导热系数,W/(m·K);Cv为定容比热容,J/(kg·K);Q为甲烷含量,t/m3;q为气体渗流速度,m/s;T0为参考温度,K。
1.4 交叉耦合方程
在热流固耦合过程中,煤岩的孔隙度和渗透率为气体压力、温度场和岩石变形(或应力场)的函数,其表达式为[3,12,17-20]

(8)
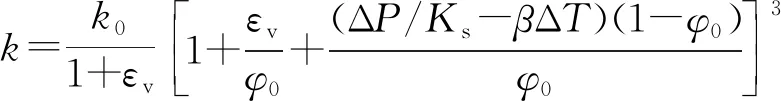
(9)
式中:φ0为初始孔隙度;k0为初始渗透率,m2。式(8)、式(9)体现了煤层气吸附、解吸、压缩、温度-渗流-应力耦合影响作用下岩石渗透率和孔隙度的不用机制,体现了热流固耦合作用下煤岩孔渗演化规律。
2 计算模型和方案
2.1 模型简介
由于三维热流固耦合问题计算量巨大,为节省计算成本,选取边长为1 m×1 m×1 m的表征单元体(representation elementary volume, RVE)作为物理模型,RVE中间含有半径为0.2 m的钻井井眼。采用四面体单元对RVE进行三维网格划分,共计有34 878个四面体单元;为准确模拟井周的应力集中现象,在井眼附近进行局部网格加密处理,如图1所示。此外,时间导数离散项采用隐式格式,自适应时间步长,并采用Petrov-Galerkin有限元格式,可以确保热流固耦合模型的计算稳定性[17-24]。

图1 三维网格剖分示意图Fig.1 Diagram of three-dimensional mesh generation
边界条件定义如下:①固体力学模块:对表征单元体RVE的六个面采用Roller边界条件,井筒采用自由边界条件;②流动压力模块:对表征单元体RVE六个面采用恒流量边界条件,井筒采用恒压边界条件;③热传导模块:对表征单元体RVE所有边界采用绝热边界条件。
2.2 非均质性表征
Weibull分布是描述岩石非均质性的一种有效方法[10,20],具体计算时使得岩石的某些物理参数服从Weibull分布,这些物理参数的随机赋值通过Monte Carlo法实现,从而实现对岩石非均质性的描述。Weibull的概率密度函数表达式为[3]

(10)
式(10)中:x为随机变量,可取弹性模量、渗透率等物理参数;m为形状参数,表示非均质程度大小,m值越小,岩石非均质性越强;n为随机变量参数的平均值。
如图2所示,考虑煤岩弹性模量的随机分布,图2(a)、图2(b)分别为表征单元体内弹性模量的三维分布云图和不同平面处的切面云图,m=7,弹性模量平均值n=1.85 GPa。

图2 煤岩三维力学非均质性表征Fig.2 Three-dimensional mechanical heterogeneity characterization of coal rock
2.3 数值模拟参数及方案
有限元模型的输入参数如表1所示,分别模拟均质地层、非均质参数m=7时的热流固耦合过程,获得应力场、温度场和压力场的三维分布,并分析不同条件下井周孔隙度、渗透率随时间、距离井眼距离的变化规律。

表1 模型输入参数
3 模拟结果
3.1 均质性煤岩的数值模拟结果
在均质弹性模量情况下,不同时刻煤岩渗透率与孔隙度随井眼距离的变化曲线如图3所示,可以看出,随开采时间增加,煤岩井筒附近的渗透率与孔隙度呈现下降趋势,开采前期,下降速度较快;当开采时间达到106s后下降速度减慢;随着井眼距离的增加,煤岩井筒附近的渗透率与孔隙度也呈现下降趋势,在距离井眼0.2 m以内区域,下降幅度较小,而在距离井眼0.2 m以外地方,渗透率与孔隙度下降速度较快。
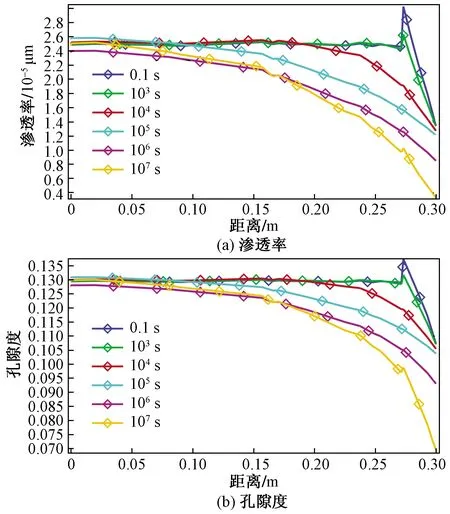
图3 不同时刻煤岩孔隙度与渗透率随井眼距离的变化曲线Fig.3 The variation curve of coal porosity and permeability with borehole distance at different time
煤岩表征单元体的三维位移场、孔隙压力场和温度场分布云图如图4~图6所示。从位移场云图可以看出,井筒附近位移场数值较大,说明井筒周围发生了应力集中现象,应力集中区域随着开采时间增加也逐渐向井筒外围波及;从压力场云图上看,井周孔隙压力场呈现圆形分布特征,随着开采时间增加,压力波逐渐向井筒外波及;从温度场云图上看,随着开采时间增加,井筒附近温度也逐渐降低,这是由于甲烷的吸附、解吸作用引起的,并且随着开采时间增加,温度场波及区域也逐渐向外扩大。
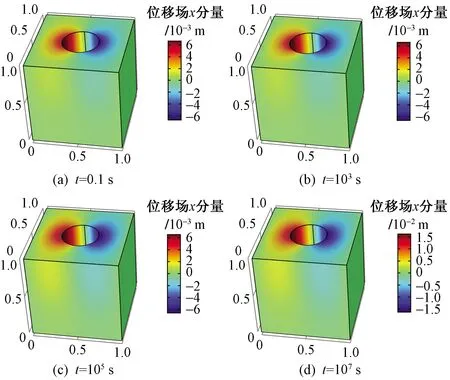
图4 不同时刻煤岩位移场x分量的三维云图Fig.4 Three-dimensional contour of x component of coal displacement field at different time
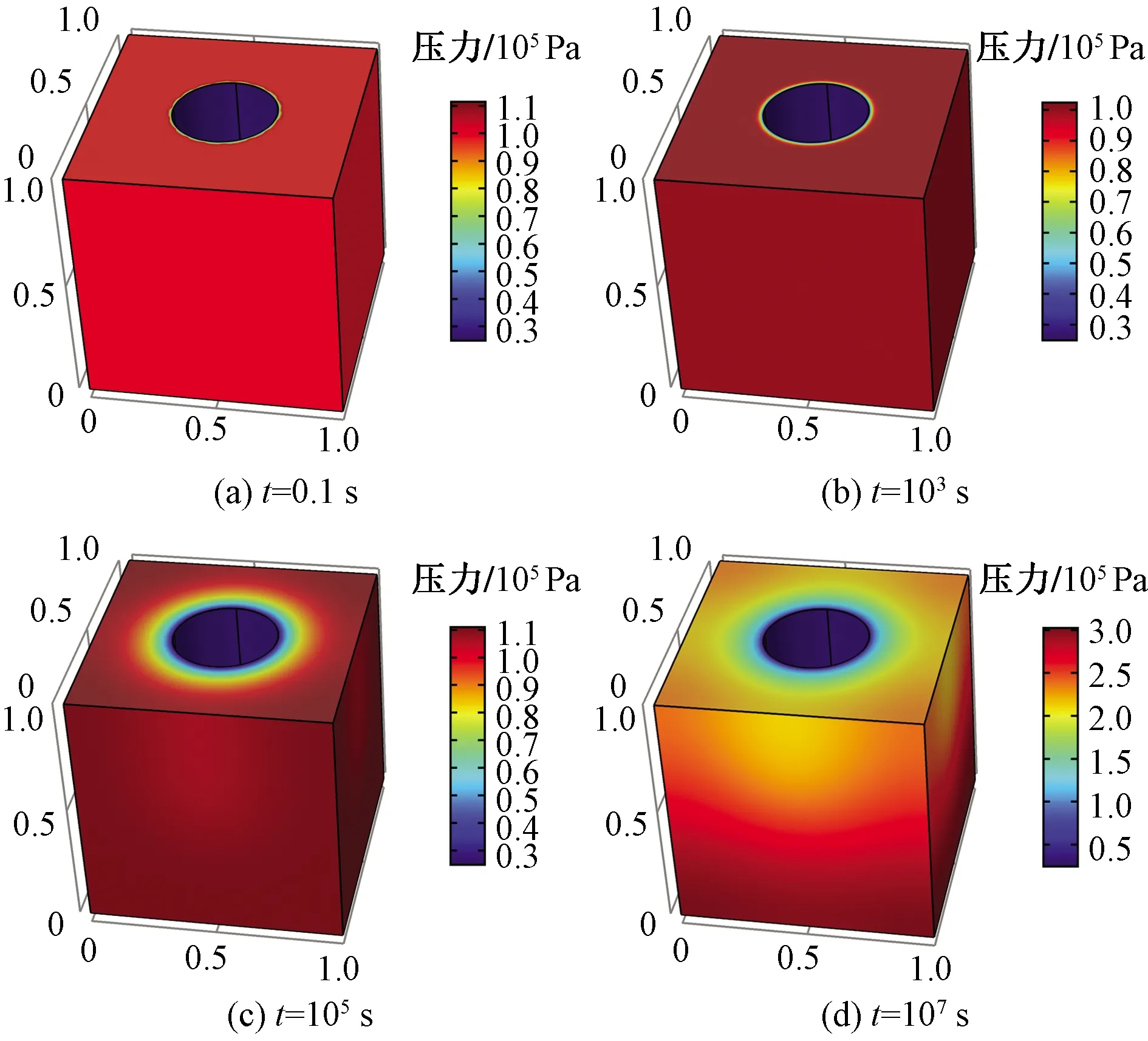
图5 不同时刻煤岩孔隙压力场的三维云图Fig.5 Three-dimensional contour of coal pore pressure field at different time
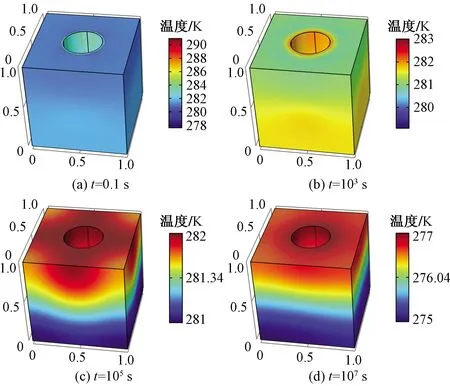
图6 不同时刻煤岩温度场的三维云图Fig.6 Three-dimensional contour of coal temperature field at different time
3.2 非均质性煤岩的数值模拟结果
在非均质弹性模量情况下,不同时刻煤岩渗透率与孔隙度随井眼距离的变化曲线如图7所示,可看出,与均质情况相比,非均质地层的渗透率与孔隙度分布呈现出波动震荡分布特征,距离井眼不同位置处的孔渗参数大小不一;随着时间增加,煤岩渗透率和孔隙度也呈现递减趋势;然而,在同一时刻,随着井眼距离增加,渗透率和孔隙度整体呈现增加趋势,与均质煤岩情况恰好相反,这是由于力学非均质性引起的。
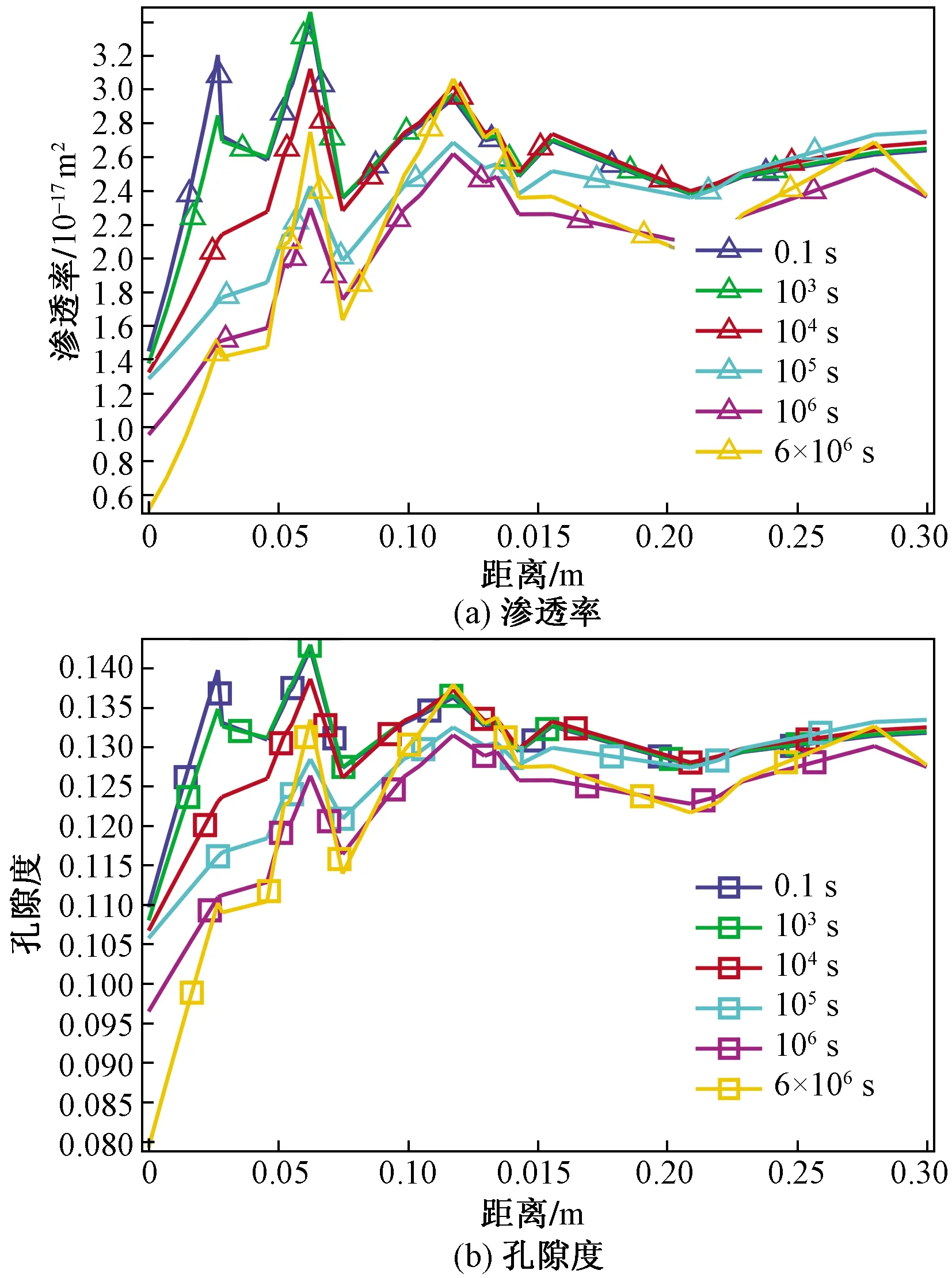
图7 不同时刻煤岩孔隙度与渗透率随井眼距离的变化曲线Fig.7 The variation curve of coal porosity and permeability with borehole distance at different time
煤岩表征单元体的应力场、孔隙压力场和温度场的二维切片分布云图如图8~图10所示。从应力场云图上看,井周的应力场分量Sxx呈现出随机分布特征,随着开采时间增加,传播区域逐渐向井筒外围扩张;从压力场云图上看,井周孔隙压力场呈现圆形分布特征,随着开采时间增加,压力波逐渐向井筒外波及,与均质情况类似;从温度场云图上看,在开采时间初期,井筒附近温度也呈现了随机分布特征;当时间达到103s以后,温度分布基本均匀;随着时间延长,温度场分布也逐渐向井筒外围传播。

图8 不同时刻煤岩应力分量Sxx的二维切片云图Fig.8 Two-dimensional slice of x component of coal stress field at different time
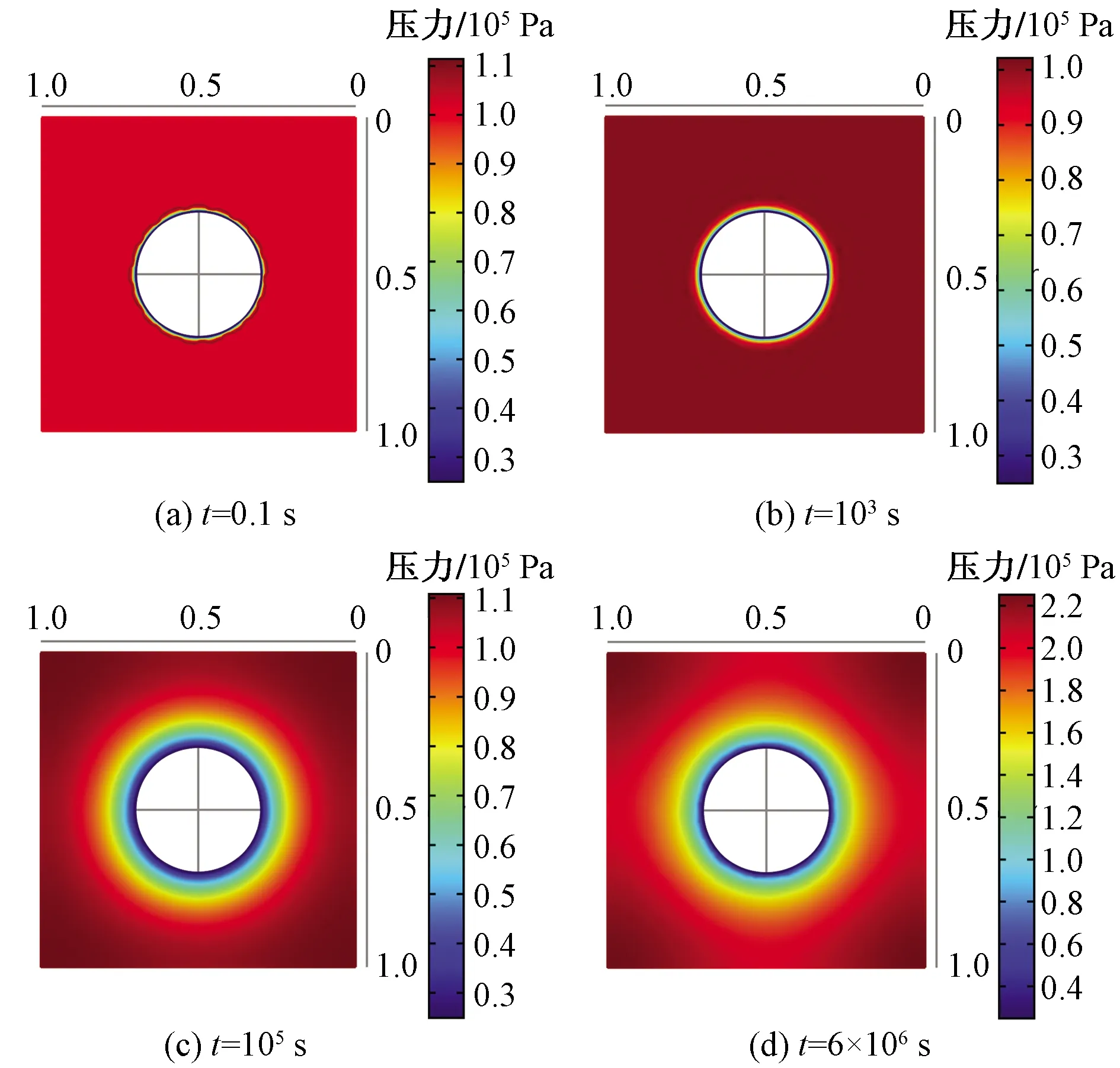
图9 不同时刻煤岩孔隙压力场的二维切片云图Fig.9 Two-dimensional slice of coal pore pressure field at different time
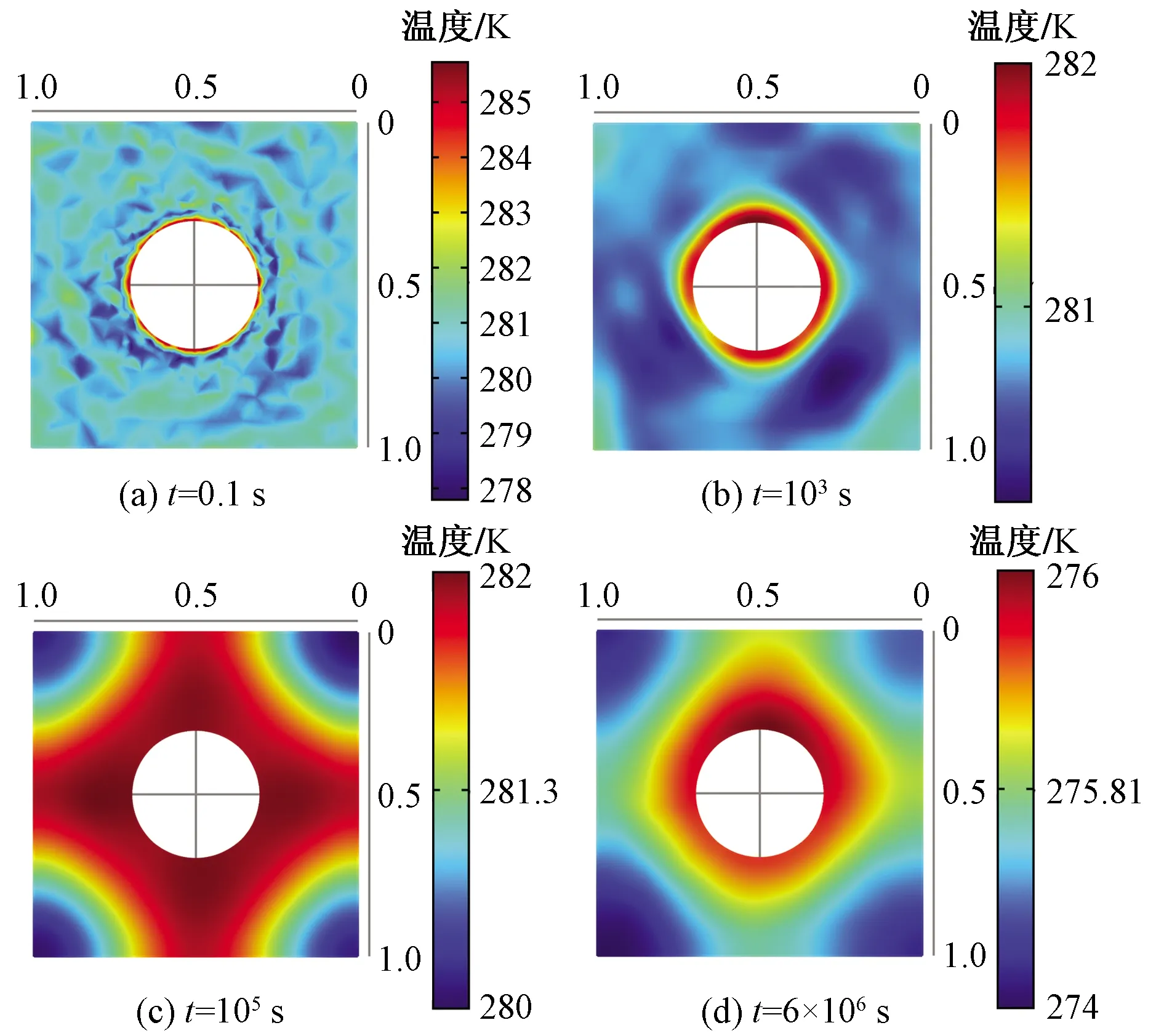
图10 不同时刻煤岩温度场的二维切片云图Fig.10 Two-dimensional slice of coal temperature field at different time
4 结论
基于Weibull随机分布函数表征煤岩力学非均质性,建立了考虑煤岩内甲烷气体解吸、吸附引起的压力变化、岩石变形和热膨胀效应的热流固耦合三维有限元模型,通过煤岩渗透率、孔隙度与热流固耦合效应间的关联式,数值模拟了煤岩渗透率、孔隙度的时空演化规律,得出如下主要结论。
(1)煤岩力学非均质性对煤岩渗透率与孔隙度影响显著,与均质煤岩相比,非均质地层的渗透率与孔隙度分布呈现出波动震荡分布特征,距离井眼不同位置处的孔渗参数大小不一。
(2)非均质煤岩渗透率和孔隙度随着开采时间增加呈现递减趋势;随着井眼距离增加,渗透率和孔隙度整体呈现增加趋势,这与均质煤岩情况恰好相反,这是由于力学非均质性引起的。
(3)非均质煤岩的孔隙度与渗透率演化是一个复杂的热流固耦合过程,与力学非均质性、热膨胀效应、甲烷气体解吸引起的压力变化和煤岩骨架的应力变形密切相关。

