细晶压电涂层/基底界面裂纹热流强度因子分析

胡帅帅， 刘建生， 李俊林， 魏含玉

(1.太原科技大学材料科学与工程学院， 太原 030024； 2.周口师范学院数学与统计学院， 周口 466000； 3.太原科技大学应用科学学院， 太原 030024)

压电陶瓷材料由于其出色的性能，在生活和工业中得到了广泛的应用。材料结构的安全，是保证器件有效稳定工作的前提。目前，受制于制造工艺水平及其他不确定的因素，在材料内部或者界面结合处往往会有缺陷的存在。因此，材料界面缺陷的力学行为的研究尤为必要。近几十年来，压电材料的界面裂纹问题吸引了大量的中外学者的广泛关注[1-5]。Mishra等[6]研究了压电器件在热-电-机械加载环境下的多孔洞与裂纹的相互作用。他们利用扩展有限元法、相互作用积分法和广义Stroh公式预测了应力强度因子，最后借助MATLAB程序对裂纹间的相互作用做了数值模拟。Singh等[7]讨论了正交异性复合材料中边缘裂纹在热载荷和机械载荷共同作用下的热应力强度因子。他们借助渐近展开法将积分方程转化为一对奇异积分方程，得到了集中点载荷作用下边缘裂纹尖端应力强度因子的解析表达式并计算了在不同裂纹长度和不同导热率比下应力强度因子的数值，最后通过数值计算分析了两种不同材料的热导率比值对热应力强度因子的影响。王永健等[8]通过复变函数方法分析了压电双材料中椭圆孔边界面裂纹的反平面问题，得出了当椭圆孔退化为竖直裂纹时改变椭圆孔一边裂纹长度将对另一边裂纹裂尖场产生很大影响的结论。吕鑫等[9]借助解析函数理论和复变方法分析了一维正方准晶周期方向穿透的抛物线裂纹问题，得出了关于经典弹性理论中的一些新的结果。

以往的压电材料界面问题研究中，大多都是关于大晶粒压电材料的研究，而对于细晶粒压电材料的研究还很少。因此，结合工业的实际需求，对细晶粒压电涂层的研究就显得格外重要。基于此，提出了涂层/基底受载荷作用下的界面裂纹问题，在此基础上构建了细晶粒压电涂层/基底在热载荷下作用下的力学模型。借助傅里叶积分手段，推导出了问题的温度场，确定了热流强度因子。通过引入数值算例，分析了影响热流强度因子的相关因素，研究结果对实际工程结构的裂纹诊断具有一定的指导意义。

1 力学模型

如图1所示，将细晶粒陶瓷粉末通过热喷涂技术喷涂于压电基底表面，并将其沿Y轴方向极化形成细晶粒压电涂层/基底结构。其中，0≤y≤h1为细晶粒压电涂层，涂层厚度为h1；-h2≤y≤0为压电基底，基底厚度为h2；-l≤x≤l为Griffith型界面裂纹，裂纹长度为2l，假定裂纹表面处电绝缘、绝热；Ta、Tb分别为y=h1、y=h2处的环境温度，假设涂层/基底结构横观各向同性。

弹性场、电场的本构方程可以写为

(1)

(2)

(3)

(4)

(5)

假设温度场满足傅里叶热传导方程：

(6)

热边界连续条件可以写为

T(x,0+)=T(x,0-), |x|≥l

(7)

T(x,h1)=Ta(x),T(x,h2)=Tb(x), |x|≥0

(8)

(9)

式中：Ta(x)、Tb(x)表示环境温度；Q0(x)表示对模型所施加的热流。

2 温度场

利用积分变换，可以将温度场的表达式表示为

(10)

式(10)中：i为虚数单位；s为引入的变量；A1j(s)、A2j(s)为待定的未知函数，j=1,2。

为了确定温度场，引入密度函数，其表达式为

(11)

根据边界连续条件[式(7)]，密度函数G(x)应满足以下单值条件：

(12)

式(12)中：t为引入的变量。

将式(11)代入热边界连续条件式(7)～式(9)，可得

A11(s)+A21(s)-A12(s)-A22(s)=

(13)

(14)

A11(s)e-|s| k1h1+A21(s)e|s| k1h1=

(15)

A12(s)e-|s| k2h2+A22(s)e|s| k2h2=

(16)

式(13)～式(16)可以改写为

AB=C

(17)

式中：

B=[A11(s),A21(s),A12(s),A22(s)]T；

C=[0,I0,I1,I2]T。

求解式(17)，可得

A11(s)=F1I0-F2I1+F3I2

(18)

A21=F4I1-F5I0-F6I2

(19)

A12(s)=F7I2+F8I0-F9I1

(20)

A22(s)=F10I1-F11I2-F12I0

(21)

式中：

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

显然，只要确定了I0就可以求解出未知函数A1j(s)、A2j(s)，从而就得到了温度场。

将式(10)代入热边界连续条件[式(9)]，可得

(35)

式(35)中：

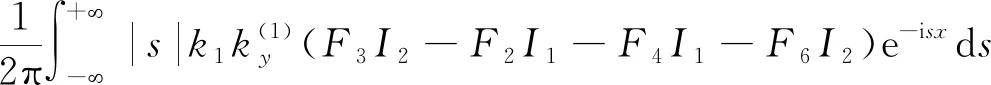
(36)

对式(35)做进一步整理，可得

Q0(x)-d0(x)

(37)

式(37)中：

(38)

式(38)中：M(s)表示关于变量s的函数。

对式(37)改变积分次序，可得

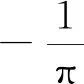
Q0(x)-d0(x)

(39)

式(39)中：

(40)

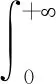
(41)

式(39)是具有柯西核的奇异积分方程，密度函数G(t)具有平方根奇异性的形式。因此，密度函数G(t)可以表示为

(42)

式(42)中：g0(t)为定义在区间 [-l,l]上的连续函数。

3 热流强度因子

由文献[10]可知，热流强度因子可以定义为

(43)

(44)

式中：L、R分别表示裂纹的左右尖端。

(45)

(46)

将式(42)代入式(45)和式(46)，可得

(47)

(48)

利用切比雪夫多项式配点法，即可求解出g0(-l)和g0(l) 的值。

4 数值计算

为了分析材料参数、裂纹尺寸，涂层厚度对热流强度因子的影响，接下来选取硒化镉压电陶瓷作为基底材料，细晶粒硒化镉陶瓷作为涂层材料进行数值计算。由文献[11]可知，通过合适的加工工艺可以使细晶粒压电材料的压电、介电性能达到大晶粒压电材料的压电、介电水平，而材料的弹性模量有显著增加。因此，在数值计算中，假设细晶粒硒化镉陶瓷涂层和普通的硒化镉压电陶瓷基底具有相同的压电、介电常数。

热流强度因子可以写为

(49)

(50)

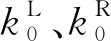
从图2中可以看出，热流强度因子随着涂层厚度的增加而不断的减小，并逐渐趋于稳定，且涂层与基底弹性模量比值较大者的热流强度因子具有较高的峰值。这表明，当涂层厚度较厚时对热流强度因子是不敏感的。由于细晶粒压电陶瓷材料相较于同种大晶粒压电陶瓷材料可以把基片做得更薄，且具有更高的弹性模量，因此细晶粒压电陶瓷材料具有更广泛的工程意义。图3给出了热流强度因子随裂纹长度发生变化的规律。

图2 热流强度因子与涂层厚度之间的关系Fig.2 Relationship between thermal strength factor and coating thickness

从图3中可以看出，当涂层厚度较小时，热流强度因子随着裂纹长度的增加而增加。这表明，当细晶粒压电涂层/基底结构受到一定强度的热载荷时，会造成裂纹的扩展，结构的损坏。

图3 热流强度因子与裂纹尺寸之间的关系Fig.3 Relationship between thermal strength factor and crack size

5 结论

利用傅里叶积分变换方法，构造出了含Griffith型界面裂纹的细晶粒压电涂层/基底在热载荷作用下的温度场的表达式，推导出了热流强度因子的具体形式，得出如下结论。

(1)验证了涂层/基底为同一种材料时的特殊情况，得出了与以往文献相同的结论。

(2)通过数值算例分析了热流强度因子与细晶粒压电涂层的厚度及裂纹尺寸之间的关系，涂层厚度较薄时，对热流强度因子比较敏感，随着涂层厚度增加，热流强度因子逐渐趋于稳定。