利用增广雅克比矩阵的冗余机械臂逆运动学求解算法

王 腾， 张承瑞*， 陈齐志， 薛祥儒

(1.山东大学机械工程学院， 济南 250061； 2.山东大学， 高效洁净机械制造教育部重点实验室， 济南 250061)

当机械臂自身所具有的自由度多于执行给定任务所需的自由度时，机械臂存在运动学冗余。相比于非冗余机械臂，运动学冗余使得机械臂具备了更高的灵活性。

一般来说，运动学逆解分为封闭解[1-2]和数值解两种形式。封闭解具有很高的计算效率，这使其在实时控制中受到青睐。文献[3]在获得的与臂型角相关的解析表达式的基础上，通过优化最小势能指标确定臂型角的大小，然后对各关节位置进行了求解。文献[4]通过限制臂型角的范围，使得逆解结果不会导致机械臂发生自身碰撞。文献[5]对机械臂的构型进行了分析，并根据几何特性获得了多关节偏置机械臂的封闭解。然而封闭形式的运动学逆解只适用于特定结构的机械臂，通用性较差。数值计算方法不寻求一种解析关系[6-7]，因此适用于大多数的机械臂。为了满足实时控制需求，在实际应用中需要考虑数值逆解算法的求解效率。

梯度投影法(gradient projection method，GPM)[8]利用机械臂在雅可比矩阵零空间的“自运动”解决冗余问题。文献[9]在此基础上选用阻尼最小二乘形式的伪逆，使机械臂具备了避开奇异位姿的能力。文献[10]将阻尼最小二乘伪逆求解方法与牛顿-拉夫逊迭代方法相结合，提高了轨迹跟踪精度。文献[11]利用由碰撞检测反馈的避障向量构造目标函数，实现了机械臂在复杂场景下的避障。然而，工作空间中的封闭路径通过伪逆方法映射到关节空间后却不是封闭的，即执行循环任务时，机械臂并不能回到初始位姿，这使得机械臂的运动不可预测[12]。运动的不可重复性限制了冗余机械臂的应用范围。文献[13]将机械臂的子任务选择为优化保证可重复运动的目标函数，使机械臂的运动具备可重复性。但是将运动学冗余用于获得非冗余机械臂的基本特性，并没有发挥出冗余机械臂应有的优势。虽然通过加权可以使目标函数结合多种优化准则，但由于优化能力有限，任务的执行效果会受到影响。

增广雅克比矩阵方法通过添加作为额外约束的优化任务，对原始任务进行增广以解决冗余[14]。该方法能够保证机械臂运动的可重复性，但随着机械臂关节数目的增多，约束条件的计算难度增大。为解决增广雅可比矩阵方法中约束计算复杂的问题，提出了一种冗余机械臂逆运动学求解算法。该算法采用分解求解策略，实现对复杂的约束条件的计算，求解效率高，可实际应用于七自由度冗余机械臂的实时控制。现以避关节极限准则作为约束条件增广雅可比矩阵，采用提出的分解计算策略对约束条件进行分解，计算获得增广部分的数值结果，在笛卡尔空间进行轨迹规划后，利用增广雅可比矩阵计算出关节速度，对关节速度积分得到关节位置，完成逆运动学的求解。

1 运动学冗余求解方法

对于具有n个关节的机械臂，定义qi(i=1,2,…,n)表示第i个关节的位置，则机械臂的位姿可由向量q=[q1,q2,…,qn]T唯一确定。维度为m的向量x表示机械臂末端相对于基坐标的位置与姿态。当n>m时，对于给定的任务来说，机械臂是运动学冗余的，冗余自由度r=n-m。关节空间与笛卡尔空间之间的关系由正运动学公式表示为

x=f(q)

(1)

式(1)中：f为与关节位置和机械臂连杆参数有关的非线性向量函数,f:Rn→Rm。

对时间求导，得到速度层面的运动学关系为

(2)

1.1 梯度投影法

微分运动学的最小范数解为

(3)

式(3)中：J†=JT(JJT)-1为雅克比矩阵J的Moore-Penrose伪逆。在式(3)的基础上增加一个齐次项，则微分运动学的通解可以表示为

(4)

式(4)中：In为n×n的单位阵；z为n维的任意向量；In-J†J为J的零空间的投影算子。式(4)使得冗余机械臂具备在跟踪目标轨迹的过程中，利用“自运动”执行与优化准则相关的子任务的能力。

令H(q)为选定的目标函数，要最小化H(q)，那么z可以表示为

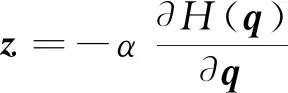
(5)

式(5)中：α为标量正实数，其数值的大小影响优化的收敛速率。

1.2 增广雅可比矩阵方法

引入跟踪轨迹之外的任务扩展任务空间，则机械臂在运动过程中会受到额外任务的约束。将机械臂的额外任务选择为在运动中满足给定的准则，那么机械臂的运动也可以看作是在运动学公式的约束下优化相关的目标函数H(q)。优化问题可以表示为

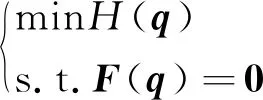
(6)

式(6)中：F(q)=f(q)-x由运动学公式获得，表示运动学约束函数。

当目标函数H(q)取极值时，H(q)的梯度在雅克比矩阵零空间上的投影为零[14]。假定q0为使目标函数局部最优的非奇异位姿，那么存在的关系为

(7)

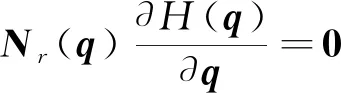
(8)

式(8)中：Nr为由In-J†J中线性独立的行所组成的r×n的矩阵。

将式(8)作为运动学公式的额外约束，那么机械臂运动过程中所要遵循的条件可表示为

(9)

对式(9)两侧求导，能够获得增广后的微分运动学公式为

(10)

(11)

对于工作空间中任意给定的点，求解式(11)能获得唯一相对应的位姿，这是机械臂运动具备可重复性的表现。

2 冗余机械臂逆运动学求解算法

利用增广雅可比矩阵方法求解逆运动学问题，关键是雅可比矩阵增广部分的计算。本文算法从增广部分的形式和计算方法两方面入手，解决机械臂关节数目较多时，增广部分计算复杂的问题。

2.1 增广部分推导

式(6)所表示的优化问题可使用拉格朗日乘子法求解[15]。通过构建拉格朗日函数，可以将带约束的优化问题转换为无约束的形式。定义拉格朗日函数为

L(q,λ)=H(q)+λTF(q)

(12)

式(12)中：λ为m维的拉格朗日乘子向量。

拉格朗日函数取极值时满足：

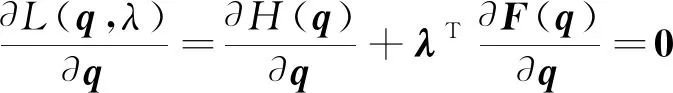
(13)

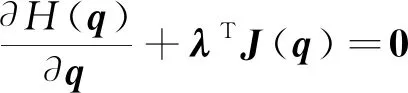
(14)

根据式(14)，文献[15]推导出额外约束公式，可表示为

(15)

定义Ji(i=1,2,…,n)为J的第i列。式(15)中，投影算子Z为(n-m)×n的矩阵，它由J的零空间的n-m个线性独立的行向量组成，其表达式为

(16)

式(15)形式下的额外约束的导数矩阵Ca为

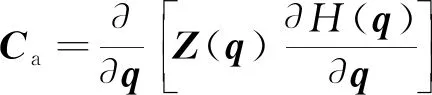
(17)

对比式(15)与式(16)中投影算子的形式可以看出，由于涉及雅可比矩阵的伪逆J†，使得Nr计算复杂。由式(16)可以看出，Z的计算主要与雅可比矩阵的列有关，利用矢量积方法[16]得出雅可比矩阵后，很容易便能确定所需的列向量。更重要的是，矩阵的逆运算仅涉及形式简单的单个矩阵，与J†相比，计算量大幅减小。为构造增广雅可比矩阵，需要将额外约束相对于关节位置向量的偏导数作为矩阵的增广部分。然而，对于实际使用的七自由度冗余机械臂来说，计算Z已经足够复杂，对矩阵的增广部分的计算就变得更加困难。

2.2 增广部分分解计算

为计算Ca的数值结果，对式(17)做进一步分解。当n-m=1时，Ca可以表示为

(18)

为了进一步减少计算量，应尽可能地避免对目标函数进行两次求导运算。实际上，一个简单且有效的目标函数能够提供显式的导数表达式，这样二阶导数值可以仅通过对显式的导数表达式进行一次求导而获得。避关节极限准则[17]可以选作目标函数，其定义为

(19)

式(19)中：qi,min和qi,max分别为第i个关节的位置qi的上限和下限。

2.3 算法流程

求解冗余逆运动学问题的算法流程如下。

Step 1利用矢量积方法计算雅可比矩阵J。

Step 4利用Ca对J增广，构造增广雅可比矩阵Je。

Step 5计算Je的逆矩阵。

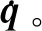
3 仿真及实验验证

为验证本文方法的有效性，首先通过仿真与梯度投影法进行对比，然后将其应用于如图1所示的7自由度(degree of freedom, DOF)冗余机械臂的实时控制。机械臂的MDH(modified Denavit-Hartenberg)参数如表1所示。选用式(19)作为两种方法中被优化的目标函数，以避免运动过程中机械臂关节位置超出限位。机械臂各关节的运动范围如表2所示。

图1 7自由度冗余机械臂Fig.1 7-DOF redundant manipulator

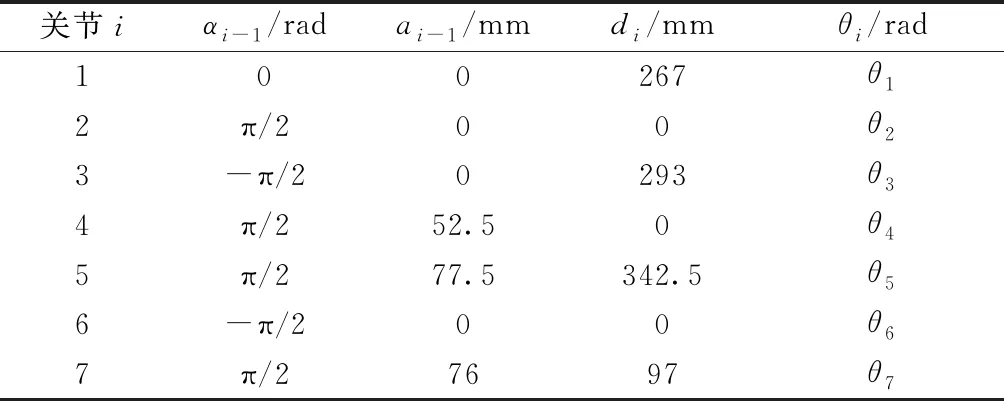
表1 机械臂MDH参数

表2 机械臂关节运动范围

3.1 仿真对比

为评估本文算法的性能表现，使机械臂末端姿态保持不变，从A点开始，按逆时针方向，沿如图2所示的空间四边形封闭路径运动。机械臂的初始位姿q=[-10°,-20°,0°,65°,10°,-50°,35°]T。四边形路径的顶点分别为A(507.02,-84.91,234.01)、B(507.02,75.09,234.01)、C(487.02,75.09,394.01)、D(487.02,-84.91,394.01)。该路径分为AB、BC、CD、DA四段，每段分别使用S曲线[18]进行加减速规划，规划后机械臂末端的位置、速度变化曲线分别如图3、图4所示。

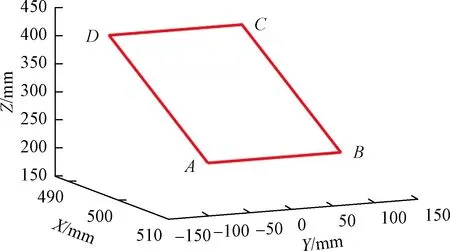
图2 笛卡尔空间封闭路径Fig.2 Closed path in Cartesian space

图3 机械臂末端规划位置Fig.3 Planned position of the end-effector of the manipulator

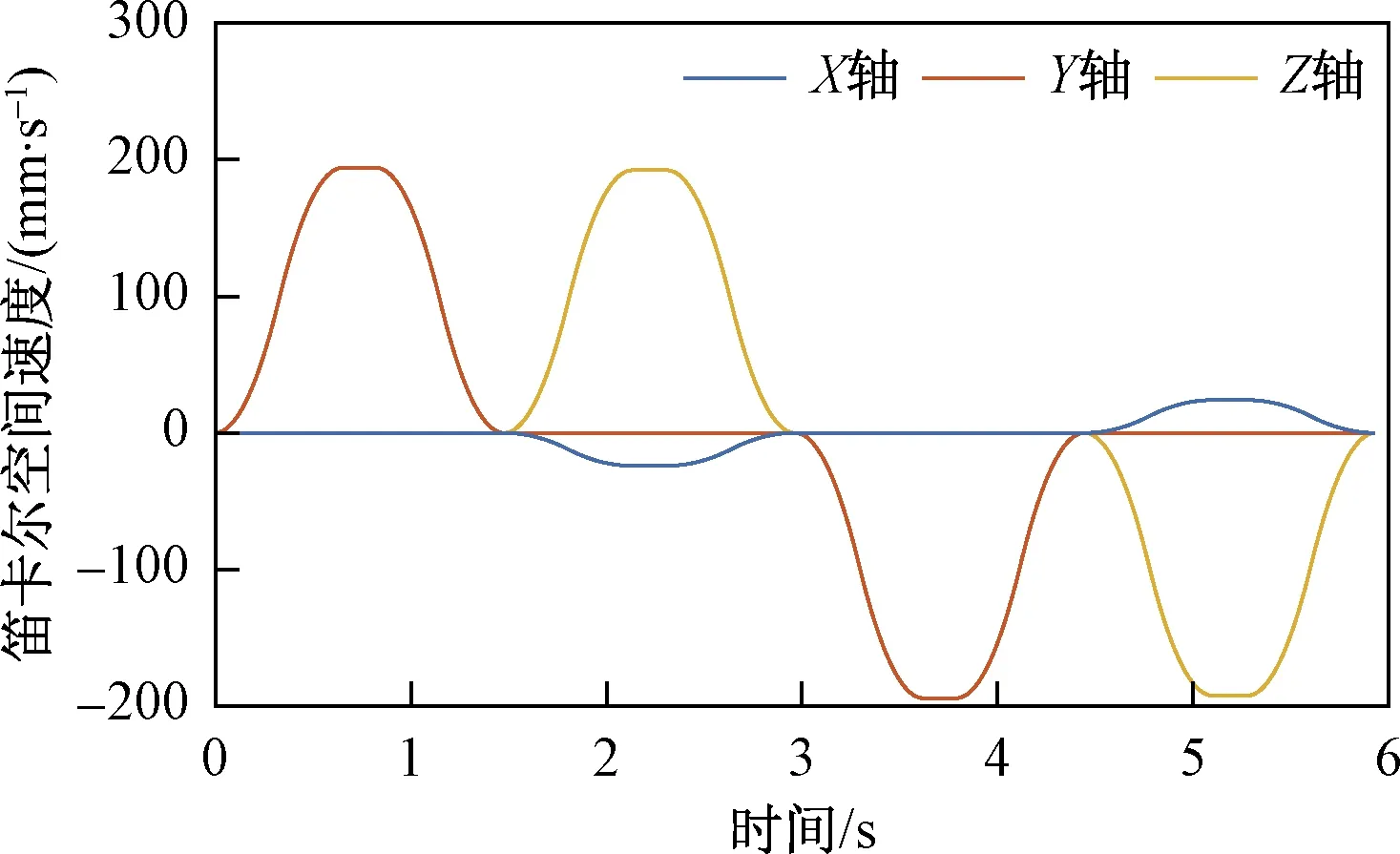
图4 机械臂末端规划速度Fig.4 Planned velocity of the end-effector of the manipulator

整个运动过程中，机械臂各关节的位置变化曲线如图5所示。可以看出，曲线光滑连续，关节位置都在允许的范围内。在相同的起始位姿下，利用梯度投影法跟踪同样的空间封闭四边形轨迹。如图6所示，关节位置同样没有超出限位。两种方法都利用运动学冗余对目标函数实现了很好的优化。

图5 本文方法获得的关节位置Fig.5 Joint position obtained by the proposed method

图6 梯度投影法获得的关节位置Fig.6 Joint position obtained by the gradient projection method

利用两种方法跟踪封闭轨迹后，各个关节始末位置的对比如表3所示。在机械臂末端回到起始位置时，本文方法使机械臂的位姿与初始位姿相同，这使得运动具有可重复性，而使用梯度投影法(gradient projection method，GPM)时，关节的最终位置相对于初始位置发生了偏移。

表3 机械臂关节始末位置对比

逆运动学问题求解的准确性影响到机械臂跟踪目标轨迹时的精度，将两种方法下的机械臂末端轨迹与期望轨迹进行对比，得到如图7所示的位置误差。本文方法对轨迹实现了准确的跟踪，梯度投影法Z轴方向的误差相对较大，X轴和Y轴方向的精度较高，但误差仍略大于本文方法。本文方法相对于梯度投影法，在轨迹跟踪过程逆运动学的精确求解上具有很好的表现。

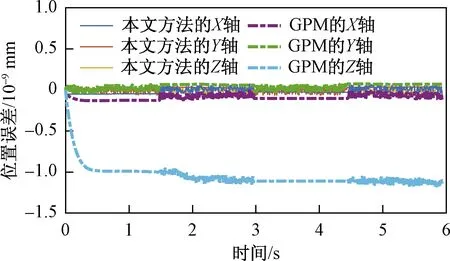
图7 机械臂末端轨迹误差Fig.7 Trajectory error of the end-effector of the manipulator

3.2 轨迹跟踪实验

本文算法由C++实现，控制程序运行在配置为Intel(R) Core(TM) i5-3437U 1.90 GHz CPU、4 GB内存的PC上，由实时拓展套件KRTS(kithara realtime suite)提供PC的实时操作系统。实验系统的通信采用自主研发的EtherMAC(ethernet for manufacture automation control)[19]总线，通过网关与支持RS-485通信的机械臂连接，通信周期为8 ms。利用本文算法进行10 000次逆解运算，平均计算时间为176 μs，求解速度能够满足实时控制的要求。

如图8所示，使机械臂执行仿真时所采用的末端轨迹。循环运动3次，机械臂的关节位置、速度分别如图9、图10所示。可以看出，针对七自由度冗余机械臂，本文方法可保证逆运动学求解的准确性，且关节位置、速度曲线平滑。同时，关节位置变化具有周期性，表明本文方法可保证机械臂运动的可重复性。

图8 机械臂跟踪规划轨迹Fig.8 Manipulator tracking the planned trajectory

图9 机械臂实际关节位置Fig.9 Actual joint position of the manipulator

图10 机械臂实际关节速度Fig.10 Actual joint velocity of the manipulator

4 结论

提出了一种利用增广雅可比矩阵的冗余机械臂逆运动学求解算法。将优化给定的目标函数作为约束任务对机械臂的任务空间进行增广，在此基础上构造了增广雅克比矩阵。针对机械臂关节数目较多时，增广雅可比矩阵难以计算的问题，通过对其中的增广部分采用分解后计算的方式实现了增广雅可比矩阵的有效求解。仿真结果表明，相比于梯度投影法，本文方法具更高的求解精度，且能够保证机械臂追踪封闭轨迹时运动的可重复性。算法平均求解时间为176 μs，计算效率满足实时控制的要求。通过七自由度冗余机械臂轨迹跟踪实验，验证了本文方法的可行性和稳定性。