冲击荷载下含裂纹缺口三点弯动态断裂实验

岳中文， 陈翠刚， 乔亚旭， 胡耀焜， 刘劲松， 桂 越

(中国矿业大学(北京)力学与建筑工程学院， 北京 100083)

在许多实际工程中，构件难免会出现各种形式的缺口[1-3]，当构件受到外部荷载作用时容易在缺口尖端产生裂纹[4-6]，当构件再次受到外界动态载荷作用时，由缺口产生的裂纹尖端的应力场会发生改变，产生应力集中现象，从而导致开裂[7-8]。因此，研究缺口和存在的裂纹对裂纹扩展影响具有十分重要的工程意义。

近年来，中外学者对含缺口和含裂纹缺口结构的力学特性进行了研究。郎福元等[9]运用光弹性方法来求出V形缺口的应力强度因子。宋鸣等[10]运用ANSYS软件模拟双材料在受到单向拉伸和三点弯曲作用，得到了弹性模量、泊松比、缺口深度和缺口张角的改变对缺口尖端奇异应力场的影响规律。Yao等[11]运用特征分析和有限元分析相结合的方法，提出了一种V型缺口结构的应力强度因子计算方法。岳中文等[12]运用动焦散系统研究了在爆炸载荷作用下试件边界锐V型缺口端部的裂纹扩展规律。Carpinteri等[13]基于有效断裂力学准则推导得到静态条件下V型缺口的应力强度因子。Lazzarin等[14]提出基于平均应变能密度准则来求含尖锐V型构件破坏准则。Lou等[15]研究了有限宽度无裂纹和含裂纹缺口板，计算了无缺口裂纹板的缺口应力强度因子和有缺口裂纹板的缺口应力强度因子。

动态光弹性方法是研究断裂力学问题的重要实验手段之一[16-18]，现运用动态光弹方法对含裂纹缺口试件进行冲击实验，对冲击荷载作用下含裂纹缺口试件的应力分布、裂纹尖端动态应力强度因子变化规律以及裂纹扩展速度的变化规律进行讨论与分析。

1 基本原理

光弹法最早由Post[19]提出，是断裂力学领域研究裂纹扩展的常用方法。将具有应力双折射特性的材料放置在偏振光场中，材料会产生与主应力差相关的等差条纹和与主应力方向相关的等倾条纹。根据材料受力产生的条纹，可用相应公式算出与之相关的应力强度因子。

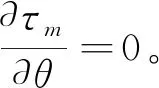
图1 裂纹尖端等差条纹图形示意图Fig.1 Schematic diagram of isochromatic fringes at crack tip

(1)

式(1)中：τm为条纹处的剪应力，θ为条纹的倾角，r为条纹的距离。由式(1)可以得到关于σox的关系式，该关系式作为混合模式指数m的函数。对于点A1、A2而言，即j=1和j=2时，σox是相同的, 因此可以得到一个关于混合模式指数m的三元方程，可以推出该三元方程的解为

KⅡ=mKⅠ,m=Hm(rm1，rm2，θm1，θm2)

(2)

式(2)中：Hm为4个几何参数的函数。Ⅰ型裂纹尖端的应力强度因子KⅠ可以表示为

(3)

式(3)中：N为条纹级数；fσ为材料的静态条纹值;h为试件厚度；rmj为条纹的距离;θm为条纹的倾角;H(θm)为修正系数。

材料在受到动态冲击破坏时，应力强度因子不能按照静态时的考虑，这时应考虑材料的应变率效应。Dally[21]在对比Irwin[20]提出的动态强度因子公式推出了一种新的Ⅰ型裂纹扩展过程中裂纹尖端应力强度因子公式，其表达式为

(4)

式(4)中：fσd为材料的动态条纹值；H(θm,a)为关于加速度a和θm的函数，其值可以查看文献[21]。

2 实验设计

2.1 实验系统

实验采用数字激光爆炸加载动光弹实验系统。图2为数字激光爆炸加载动光弹实验系统的结构示意图。该系统具有便于操作、适应性强、安全可靠等优点。

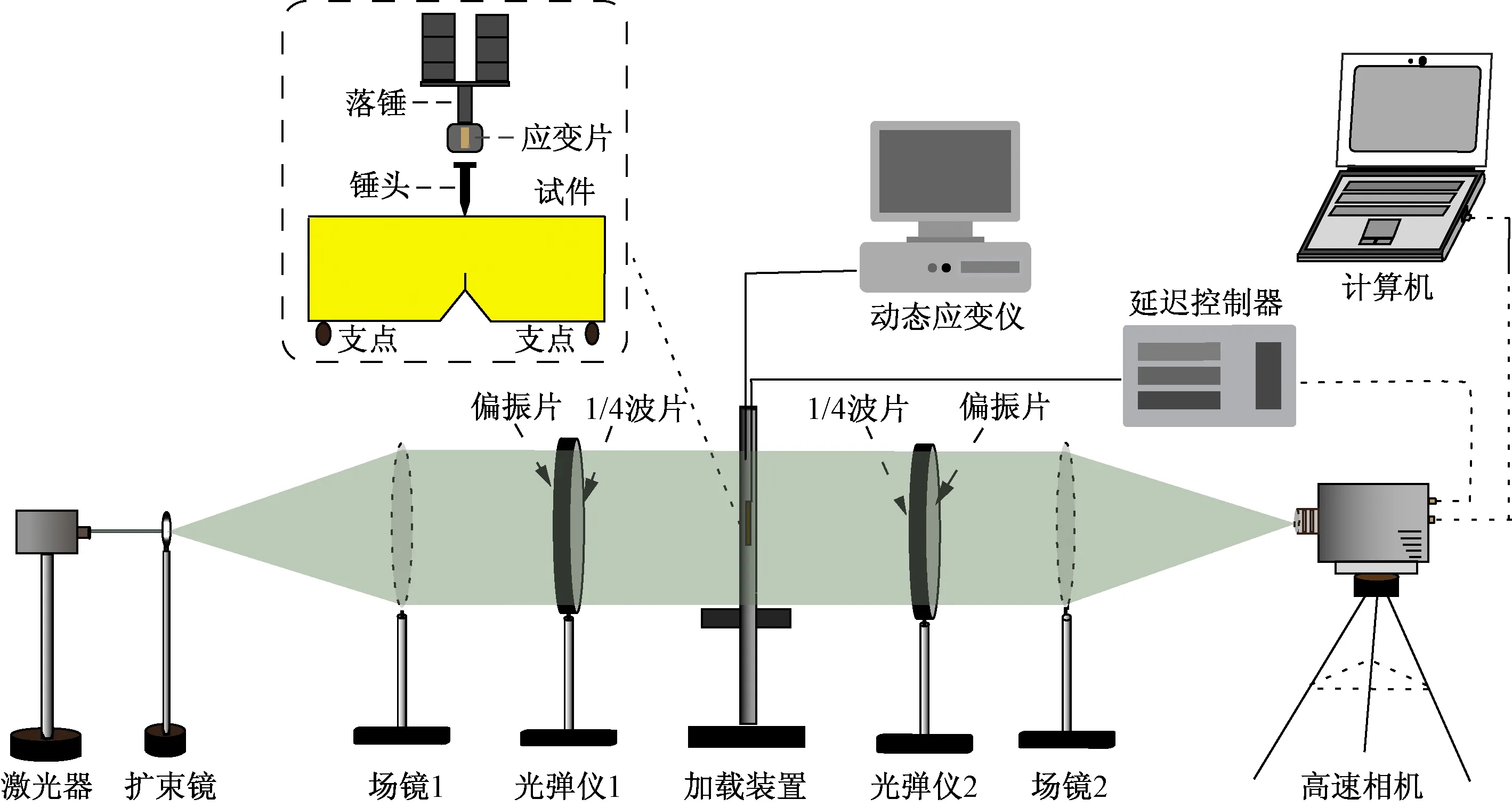
图2 数字激光动态光弹性实验系统示意图Fig.2 Schematic diagram of digital laser dynamic photoelasticity experimental system

2.2 实验尺寸设计

实验采用自制的光弹性实验专用环氧树脂板作为实验材料，基本力学参数如表1所示。图3为试件尺寸示意图。试件长L为200 mm、宽W为50 mm，厚度T为5 mm，符合三点弯国际标准试件尺寸要求。根据王启智等[22]得到的数值模拟结果可知在缺口角度不变的情况下，随着缺口深度d的增加应力集中系数会不断变化，d/W=0.2～0.3时会出现一个峰值，并且峰值更趋近于d/W=0.2，为了让实验过程中试件的应力集中区域的应力变化比其他区域更加显著，使实验效果更理想，故选择缺口深度d为10 mm。在缺口尖端使用细钢丝绳拉制预制裂纹，预制裂纹的长度a为5 mm。试件共分为5组，每组3个试件，缺口角度2β分别为30°、60°、90°、120°和150°。

表1 光弹模型基本参数Table 1 The basic mechanical parameters of photoelastic model

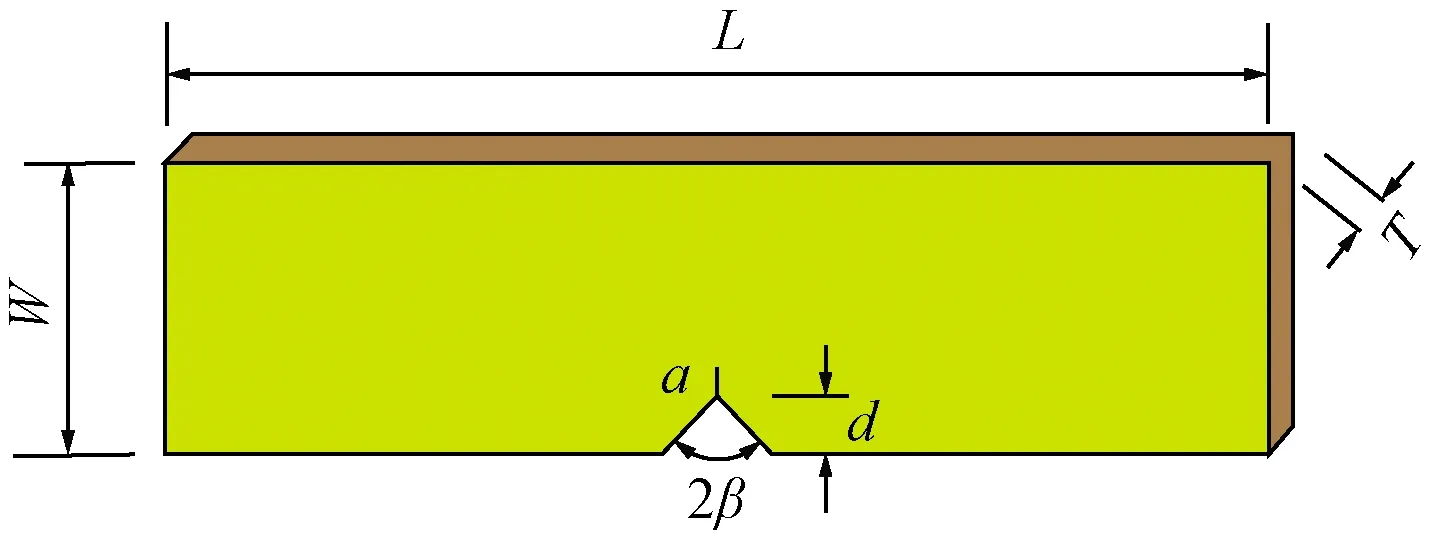
图3 试件尺寸Fig.3 Specimen size

2.3 实验方案

图4为含裂纹缺口三点弯试件冲击图。将含裂纹缺口三点弯试件放在加载平台上，使落锤冲击点刚好位于预制裂纹的正上方。底部固定夹具之间的距离为190 mm，底部缺口的中心到两个夹具的距离相等，落锤质量为1.44 kg，下落高度均为331 mm。高速相机采用外部信号触发，将落锤和锤头与延迟控制器触发通道相连，当落锤与锤头发生触碰或分开时，都会向延迟控制器发出一个触发信号，延迟控制器将信号传递给高速相机，使相机进行等差线条纹的采集和记录。实验时，光路采用圆偏振光场明场,高速相机拍摄频率设置为210 000 fps，快门速度设置为1/1 000 000 s。通过测量等差条纹，可计算得到裂纹尖端的应力强度因子KⅠ。

图4 含裂纹缺口三点弯试件冲击图Fig.4 Impact diagram of three-point bending specimen with a crack originating from the notch tip

在实验系统中的锤头上粘贴应变片，将应变片与动态应变仪相连，桥压设置为2 V，增益设置为1 000，应变仪触发方式设置为外触发，记录锤头的应变变化情况。

3 实验结果及分析

3.1 实验结果

实验采用缺口角度2β不同的试件，其等差条纹的变化规律基本一致，因此选用缺口角度2β为90°举例说明。图5为含裂纹缺口三点弯曲梁冲击实验中90°试件的等差条纹系列图片。图5中试件的等差条纹变化十分明显，可以清楚地表现出试件在冲击作用下的应力变化情况。在t=0时刻，落锤击中试件跨中位置，试件中的应力以应力波的形式开始向下传播。在t=47.62 μs时刻，试件在预制裂纹尖端开始出现应力集中，随着时间的增加，试件在预制裂纹尖端的应力集中现象越来越明显，等差条纹越来越密，并在t=160.90 μs时刻，预制裂纹尖端的等差条纹密集程度达到最大。在t=166.67 μs时刻，试件开始起裂，此时裂纹基本上呈竖直向上扩展，随着裂纹的扩展等差条纹逐渐稀疏。在t=233.33 μs时刻，裂纹扩展方向开始发生偏转，扩展方向发生偏转后试件等差条纹密集程度的变化显著减缓。最终在t=352.38 μs时刻，裂纹扩展结束，试件实现贯穿。在裂纹未扩展阶段，试件的等差条纹在逐渐增加，等差条纹密集区域主要集中在落锤加载点和预制裂纹尖端，落锤加载点的等差条纹密集程度要显著大于预制裂纹尖端。在裂纹扩展阶段，试件的等差条纹在逐渐减少，裂纹扩展未发生偏转之前的等差条纹变化情况要明显快于发生偏转之后的变化情况。从落锤击中试件到裂纹扩展发生偏转之前，试件上的应力呈现对称分布。

3.2 裂纹尖端动态应力强度因子值变化规律

图6为动态应力强度因子与时间关系曲线。在裂纹扩展末期，裂纹尖端的应力强度因子很小，等差条纹在尖端处过于稀疏，测量误差过大，故在测量等差条纹时不予考虑。以缺口角度2β为60°为例，在t=0时刻，锤头击中试件上边缘跨中位置，锤头对试件施加了冲击荷载，应力以应力波的形式由落锤击中处开始向试件下部传播；t=57.14 μs时刻，试件在缺口预制裂纹处出现明显的应力集中，此时裂纹尖端的应力强度因子KⅠ为0.184 kN/m3/2，从t=57.14 μs时刻开始，裂纹尖端的应力集中现象越来越明显，裂纹尖端的应力强度因子KⅠ逐渐增加且增加速率比较稳定；t=147.62 μs时刻，裂纹尖端的应力强度因子KⅠ达到最大值0.817 kN/m3/2，应力强度因子达到试件的起裂韧度，试件即将起裂；当t=152.38 μs时，试件由预制裂纹尖端起裂，由于试件起裂消耗了大量能量，此时裂纹尖端的应力强度因子KⅠ迅速减小为0.705 kN/m3/2，随着裂纹的扩展，能量会逐渐消耗，裂纹尖端的应力强度因子KⅠ会逐渐减小且减小速率趋于减缓，最终在t=195.24 μs时减小到0.184 kN/m3/2。比较图6中5组应力强度因子KⅠ与时间关系t曲线可以看出5组数据都符合应力强度因子KⅠ随时间t先增大后减小的趋势，可以将增加和减小分为阶段Ⅰ和阶段Ⅱ，在阶段Ⅰ中应力强度因子KⅠ随时间t的增加速率比较稳定，在阶段Ⅱ中应力强度因子KⅠ随时间t的减小速率呈现前期比较大而后趋于平缓的变化规律。由图6也可以看出，随着缺口角度2β的增加，应力强度因子KⅠ最大值有随着缺口角度2β增大而增大的变化规律，缺口角度2β在30°～90°时，应力强度因子KⅠ峰值增加比较缓慢，当缺口角度2β大于90°时，应力强度因子KⅠ峰值会显著增加。同时，缺口角度2β的增加会导致应力强度因子KⅠ峰值出现的时间有所变化，当缺口角度2β在30°～90°时，应力强度因子KⅠ峰值出现的时间没有明显变化，当缺口角度2β大于90°时，应力强度因子KⅠ峰值出现的时间会随缺口角度2β的增加而延长。裂纹尖端的应力强度因子未达到峰值之前，在某一时刻，不同缺口试件的应力强度因子KⅠ表现为随缺口角度2β的增大而减小，这表明试件裂纹尖端的应力集中程度随切口角度2β的增加而减小。

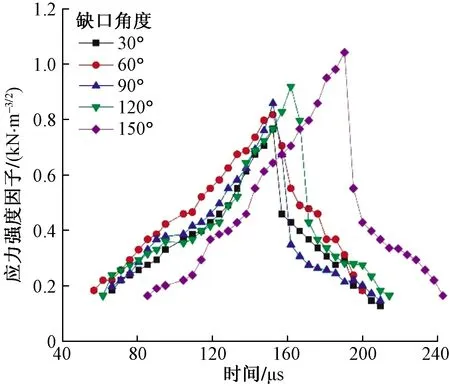
图6 动态应力强度因子与时间关系Fig.6 Relationship between dynamic stress intensity factor and time

3.3 裂纹扩展速率变化规律

图7为裂纹扩展速度与时间关系曲线。以缺口角度2β为60°为例，由图7可知，t=0时刻锤头击中含裂纹缺口试件上边缘跨中位置，在t=0～147.62 μs时间段，能量在裂纹尖端处积聚，试件始终没有起裂；t=152.38 μs时刻，裂纹扩展力等于裂纹扩展阻力，试件起裂；在t=157.14 μs时刻，由于积聚的能量迅速释放，裂纹扩展速度v快速达到315 m/s；在t=161.90～219.05 μs时间段，裂纹扩展速度v始终保持在211.44～420 m/s；在t=223.81～247.62 μs时间段，裂纹扩展方向开始偏转，裂纹扩展速度v逐渐减小，由175 m/s下降到50.18 m/s；在t=252.38～323.81 μs时间段，受到应力波反射的影响，裂纹扩展速度v震荡上升，并在t=323.81 μs时刻达到197.40 m/s；在t=323.81 μs时刻后，裂纹扩展速度v逐渐下降直至试件贯穿，此时裂纹扩展速度受边界效应影响较大。当试件缺口角度2β取其他角度时，裂纹扩展速度v随时间t的变化规律与2β取60°时相似。当试件缺口角度2β取30°、60°、90°、120°、150°时，裂纹的起裂时刻分别为152.38、152.38、157.14、161.90、180.95 μs，可见当缺口角度2β小于90°时，缺口角度2β对试件的起裂时刻影响不大，缺口角度2β大于90°时，缺口角度2β越大起裂时刻越晚，且随着角度2β的增加对试件的起裂时刻的影响越大。

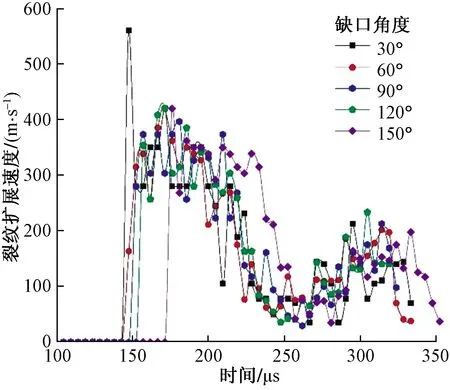
图7 裂纹扩展速度与时间关系Fig.7 Relationship between crack propagating velocity and time

3.4 应变片测得应变变化规律

图8为锤头测得应变变化。锤头处粘贴的应变片测量得到的应变因为受到应力波叠加和尺寸效应的影响不是锤头应变真实值，但测得的应变和锤头应变的真实值是正相关的，可以作为锤头真实应变的参考值。从图8可以看出，测得的锤头应变都表现出先压缩后拉伸然后逐渐震荡趋于平缓的变化规律。同时，随试件的缺口角度2β增大锤头的最大压应变会随之增大。当缺口角度2β小于90°时，最大压应变的增长趋势较为平缓；当缺口角度2β大于90°时，最大应变增长趋势显著增加。锤头所测得应变变化规律可以解释为：随着试件缺口角度2β的增加，试件破坏所需要的能量会随之增加；当切口角度小于90°时，试件破坏所需要的能量增加不明显，当切口角度大于90°时，试件破坏所需要的能量显著增加。这与通过光弹测得的应力强度因子KⅠ随角度2β的增大而增大的变化规律基本一致。

图8 锤头的应变变化Fig.8 The strain variation of the impact head

4 结论

采用动态光弹性实验方法，结合动态应变数据采集系统，对含裂纹缺口试件进行了冲击实验，得到如下结论。

(1)试件在受到冲击荷载作用后，裂纹尖端动态应力强度因子呈现先增大后减小规律，且随着缺口角度2β的增加，试件未起裂前裂纹尖端的应力集中程度越小，而裂纹尖端应力强度因子的峰值会逐渐增加。

(2)锤头应变都表现出先压缩后拉伸然后逐渐震荡趋于平缓的变化规律，随试件的缺口角度2β增大，试件破坏所需的能量增加，锤头处的最大压应变随之增大。当缺口角度2β小于90°时，试件破坏所需的能量增加不明显，最大压应变的增长趋势较为平缓；当缺口角度2β大于90°时，试件破坏所需的能量显著增加，最大压应变增长趋势显著增加。锤头的最大压应变与测得的应力强度因子变化规律基本一致。

(3)不同缺口角度试件的裂纹扩展速度随时间变化规律基本一致，都表现为：试件开始起裂后，裂纹尖端积聚的能量迅速释放，裂纹扩展速度快速上升，随后保持在一个区间内震荡，随后裂纹扩展方向发生偏转，扩展速度逐渐下降，然后由于受到应力波反射的影响，扩展速度又开始震荡上升，最后速度逐渐下降直至试件贯穿，但当缺口角度大于90°之后，试件的起裂时间显著延长。