含时密度矩阵重正化群的理论与应用
李维唐,任佳骏,帅志刚
(清华大学化学系,有机光电子与分子工程教育部重点实验室,北京100084)
1992年,由White[1,2]提出的密度矩阵重正化群(Density matrix renormalization group,DMRG)算法是研究一维量子多体强关联系统的强有力方法,尤其适用于只有最近邻相互作用的量子模型.随后,Shuai,Ramasesha和Fano等将DMRG推广到具有长程作用势的化学体系[3~6].通过将DMRG的基矢对称化,Shuai等[3~5]计算了共轭多烯的低激发态结构,为高分子发光给出了判据,并发展了基于DMRG的线性和非线性光学响应系数的计算方法.1999年,White和Martin[7]首次将DMRG用于从头算量子化学模型,随后Head-Gordon,Chan,Reiher,Yanai和Kurashige等[8~11]对DMRG算法做了大量的优化,使得量子化学DMRG成为了强关联分子体系的一种主流的方法.含时DMRG(Time-dependent DMRG,TD-DMRG)是针对分子器件的量子输运现象而提出[12],并得到快速发展[13,14].早期的TD-DMRG时间演化算法如时间步瞄准(Time-step targeting,TST)算法主要是受最初的DMRG迭代算法启发[15],后期发展的大多数TD-DMRG算法是基于矩阵乘积态(Matrix product state,MPS)的波函数拟设和矩阵乘积算符(Matrix product operator,MPO)设计的[16,17],包括一系列演化再压缩(Propagation and compression,P&C)算法[18]以及最近的基于含时变分原理(Time-dependent variational principle,TDVP)算法[19,20].只要MPS的虚拟键维数足够大,这些TD-DMRG算法可以几乎精确地给出复杂多体系统的含时薛定谔方程的解.
近年来,TD-DMRG主要被用于研究电子-声子(振动)耦合问题(简称电声耦合).电声耦合在化学反应、(生物)分子的光化学光物理过程以及固体中的输运现象中均扮演重要角色.如TD-DMRG已经被成功应用于模拟给体/受体异质结的激子分离[21,22],分子聚集体的荧光和吸收光谱[23,24]以及有机半导体的电荷迁移率[25].实际上,由于电声耦合问题在化学中的地位至关重要,早在DMRG之前,理论化学家已经开发了一整套适用于不同科学问题的理论方法来模拟电声耦合动力学过程,即非绝热动力学方法[26,27].这类方法的目标是超越玻恩-奥本海默近似,对电子和原子核的耦合运动进行描述.众多的非绝热动力学方法大体上可以分为两类:(1)利用量子力学处理原子核的运动,称为量子动力学方法,其优点是可以正确描述隧穿效应及零点振动,代表性方法是多组态含时Hartree(Multi-configuration time-dependent Hartree,MCTDH)[28,29]及其多层推广(Multi-layer MCTDH,ML-MCTDH)[30,31];(2)利用经典力学近似描述原子核的运动,称为混合量子/经典动力学方法,其优点是计算量较小,代表性方法是势能面跳跃法[32,33].TD-DMRG利用波函数描述原子核的状态,因此属于量子动力学方法.TD-DMRG与(ML-)MCTDH在非绝热动力学中的定位类似,其理论形式也有共通之处[34].在最近几年,TD-DMRG与(ML-)MCTDH相互促进,产生了一批新的算法[35~37].
本文将简述基于矩阵乘积态和矩阵乘积算符的DMRG的基础理论,并将分3类较详细地介绍现有的TD-DMRG时间演化算法,然后,介绍在TD-DMRG中引入温度效应的算法,最后,讨论TD-DMRG算法的应用,包括我们[23,25]最近利用TD-DMRG模拟分子聚集体光谱和有机半导体迁移率的一些进展.本文聚焦于TD-DMRG在电声耦合问题中的应用,如关注温度效应是因为温度对振动自由度有重要影响.然而需要强调的是,不能简单地认为TD-DMRG就是一种新兴的可以作为(ML-)MCTDH替代品的非绝热动力学方法,因为TD-DMRG算法本身并不限制于特定的模型.如最近化学领域的一些研究显示出TD-DMRG模拟基于第一性原理哈密顿的电子动力学的潜力[38,39].尽管这些研究目前只占使用TD-DMRG在化学中应用的少数,但其应用领域将会持续拓宽.关于TD-DMRG的理论与应用的更详细内容可参见相关报道[17,40].
1 基于MPS的现代DMRG理论
现代DMRG理论一般基于矩阵乘积态拟设[16].对于由N个自由度组成,每个自由度的正交归一基为的系统,任意量子态Ψ可以表示成N个矩阵的连乘积,即矩阵乘积态:

式中:{·}表示各个指标的集合.图1为矩阵乘积态的图示.ai的维数被称为(虚拟)键维数,记为M或|ai|.

Fig.1 Graphical representation of an MPS
多体重正化基定义为

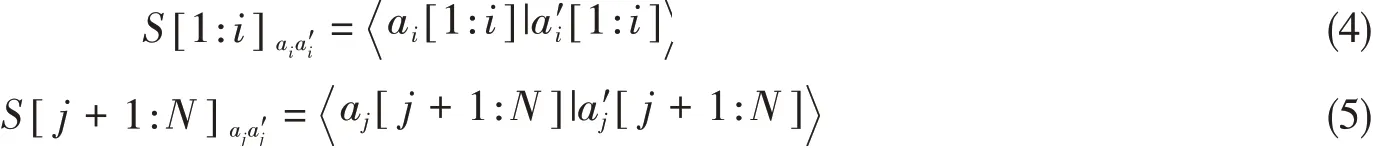
对于一个特定的量子态而言,其矩阵乘积态表示并不是唯一的.在任意两个相邻矩阵AσiAσi+1之间插入一个单位矩阵I=GG-1不改变波函数,但局域矩阵却发生了变化:所张成的空间的系数矩阵.通常,

为方便计算,可以引入额外的规范条件来消除参数的冗余性.最常见的规范条件是“混合/左/右规整化”.一个规整中心在第n个矩阵的混合规整矩阵乘积态可以写为


Lσi(Rσj)*表示Lσi(Rσj)的复共轭.
当满足式(8)和式(9)时,重正化基满足正交归一条件S[1:i]lil′i=δlil′i(i=1,2,…,n-1)和S[j+1:N]rjr′j=δrjr′j(j=n,n+1,…,N-1).当规整中心n处于最右(左)侧时,该MPS被称为是左(右)规整的.若Cσn进一步被QR分解:

式中:Lσn满足式(8),而Dlnrn是空间的系数矩阵.之后,Dlnrn与相乘,得到,即规整中心的位置向右移动了一个位置.通过与上述过程相似的RQ分解,可以将规整中心的位置向左移动一个矩阵(以下将QR分解和RQ分解统称为QR分解).通常,一个规整中心在第n个矩阵上的MPS可以由任意MPS做连续的QR分解得到,这一过程称为规整化.
若利用奇异值分解(Singular value decomposition,SVD)代替式(10)中的QR分解:

式中:Λ是一个对角元从大到小排列的实对角矩阵并且若是归一化的,则满足式(8).若所有的都被保留,并且向右移动规整中心那么MPS所表示的波函数不发生变化,SVD的作用与QR分解相同.然而,如果只保留最大的M项(M<k)以得到那么从数学上来说将会是的一个好的近似,且M更小.若是归一化的,由截断所带来的误差可以由衡量.基于这个算法,一个左(右)规整的矩阵乘积态可以通过从第N个到第1个(从第1个到第N个)矩阵的连续SVD“压缩”得到其M更小的近似在每一步截断时,有两种常用的标准.第一种是截断至预先指定的虚拟键维数M.第二种是保留所有大于预先指定阈值的Λss.
除了规整化操作和压缩操作,MPS结构还允许其它一些常见操作,如与MPS相似,常见的量子算符可以表示成矩阵乘积算符(MPO)的形式[16,41]:

图2为MPO的图示.

Fig.2 Graphical representation of an MPO
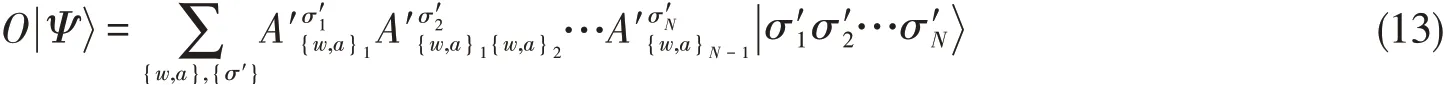
其中


其中

2 时间演化算法
TD-DMRG的时间演化算法种类繁多,但大体上可以分为3类.(1)对时间演化算符e-iHt或进行基于MPO/MPS全局的近似.这类方法包括龙格-库塔(Runge-Kutta,RK)方法[18,23]、时间演化块消减(Time-evolving block decimation,TEBD)方法[14,42,43]、WI,II方法[44]、Krylov子空间方法[18,45]、Chebyshev展开方法[46]以及分裂算符方法等[47].这些方法的共通点是在每一步时间演化时,波函数MPS首先通过MPO/MPS乘法和MPS/MPS加法作为一个整体演化(Propagate)形成具有更大虚拟键维数的MPS,随后依据原本的M或奇异值截断阈值进行压缩(Compress).因此这类算法被称为P&C算法.(2)基于含时变分原理(TDVP)[48].依据不同的推导运动方程的方式,这类方法有固定规范自由度[19]和投影算符裂分(Projector-splitting,PS)[20]两个变种.(3)受原本的基态DMRG算法启发,利用平均约化密度矩阵来更新重正化基.其代表性方法是时间步瞄准方法[15]及一些变种[38,49].除了TEBD之外,所有上述时间演化算法都适用于具有长程相互作用的模型.此外P&C算法是在现代MPS/MPO框架下最直接的时间演化算法,而PS算法是最近最常被使用的算法[24,25,50~52].从数值计算的角度上来说,所有的时间演化算法都需要进行大量的矩阵乘法运算,可以有效被图形处理器(Graphical processing units,GPU)所加速.GPU加速不同类型算法的加速比有差异.不需要压缩维数较大的MPS的算法可以最大程度上被GPU加速,加速比可以达到数十倍[37].这类算法主要是基于TDVP的算法.
2.1 演化并压缩算法

为简便起见,采用原子单位,设ℏ为1.基于最简单的前向欧拉法,对每一时间步τ应该按照下式演化Ψ:

正如前文所介绍,MPO/MPS乘法和MPS/MPS加法是MPS的常规操作,因此式(18)可以很方便地转换成一个TD-DMRG算法.通过式(18)获得的往往比初始态具有更大的虚拟键维数,所以在下一步迭代之前需要对进行压缩.这一具有两个步骤的算法因而被称为是P&C算法.
对这一简单算法的一个直接改进是将具有一阶误差的前向欧拉积分法替换为经典的具有四阶误差的龙格-库塔(RK4)积分法[18,23]:

对于不含时的哈密顿来说,RK4算法与形式时间演化算符e-iHτ的四阶泰勒展开等价:
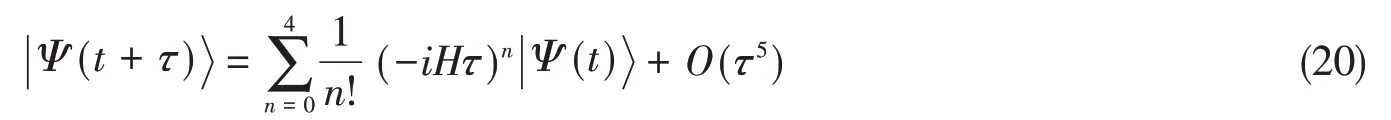
在实际计算时,第n阶项可以由第n-1阶项作用H计算得到.
其它P&C算法虽然理论基础各不相同,但具体到TD-DMRG算法与本文介绍的基本类似.其中,TEBD算法是最著名的P&C算法之一[14,42,43],虽然该算法具有很高的效率且易于实现,但是其不能被直接用于具有长程相互作用的模型,因此在化学中的应用受到一定限制[21,22].假设一个具有2N个自由度的系统可以由只有最近邻相互作用的哈密顿描述:

式中:hj,j+1作用于第j和第j+1个自由度.观察到哈密顿可以分为两个部分H=H1+H2:

按照这种划分方式,一阶Trotter分解可以将e-iHτ分为两部分乘积:

尽管H1和H2相互并不对易,H1和H2中的各个项相互对易,因此:

连乘中的每一项e-ihτ都可以表示成一个两个格点的MPO,即都可以被有效地表示为MPO.将这些算符作用到上后进行压缩就完成了时间演化中的一步.同理也可以构造二阶Trotter分解:

对于具有长程相互作用的体系,TEBD需要和其它技术结合,如引入交换门[53]或在电声耦合模型中对系统哈密顿做变换[54].此外,Trotter分解的技术也可以和泰勒展开时间演化算符的做法相结合[47].其思路是将动能部分从哈密顿中分离出去,以减小时间演化算符中的MPO的虚拟键维数.
WI,II方法[44]试图基于哈密顿H的形式显式地将时间演化算符e-iHτ近似为一个MPO.该方法与RK算法相比的优势是其每一个自由度平均的积分误差是一个常数.
Krylov子空间方法(也被称为Lanczos方法)是近似的有效方法[18,45].Krylov子空间的定义是由向量所张成的空间,维数是N.这些向量一般不是正交归一的,正交归一化后得到的向量称为Krylov向量{k0,k1,…,kN-1}.Krylov子空间方法的总体目标是找到在Krylov子空间中的最佳近似.当N等于原本的希尔伯特空间维数时,该方法就是精确的.在实际计算中,往往少数Krylov向量就可以得到误差非常小的结果.向Krylov子空间投影的投影算符定义如下:


Chebyshev展开方法利用Chebyshev多项式展开e-iHt[46].Chebyshev向量依据以下递推关系计算:

式中,φ0(t)=c0(t),φn>0=2cn(t),而cn(t)的定义为

式中,Jn是第一类Bessel函数.
在所有P&C时间演化方法中,目前应用最广泛的是基于e-iHτ的泰勒展开的方法,TEBD方法和Krylov子空间方法.对于只具有最近邻相互作用或可以转化成只具有最近邻相互作用的哈密顿来说,TEBD在易于实现和较高精度间取得了较好的平衡[51,55~57].对于一般的哈密顿而言,基于e-iHτ的泰勒展开的方法最容易实现[23,47],但精度不如Krylov子空间方法[39].
2.2 基于含时变分原理的算法
Rayleigh-Ritz变分原理被广泛用于寻找不含时哈密顿的近似基态.类似地,含时变分原理(TDVP)也是在已知初始态时寻找最佳的近似含时波函数的有力工具.Dirac-Frenkel含时变分原理[48,58]为

在实时演化中,TDVP可以保证波函数的模和体系能量守恒[58].这两个特性对于可靠的长时间动力学非常重要.从几何的角度而言,TDVP可以理解成是将正交投影到在当前时间的切空间中:

其中,P是由切空间中正交归一的向量构造成的投影算符,定义为

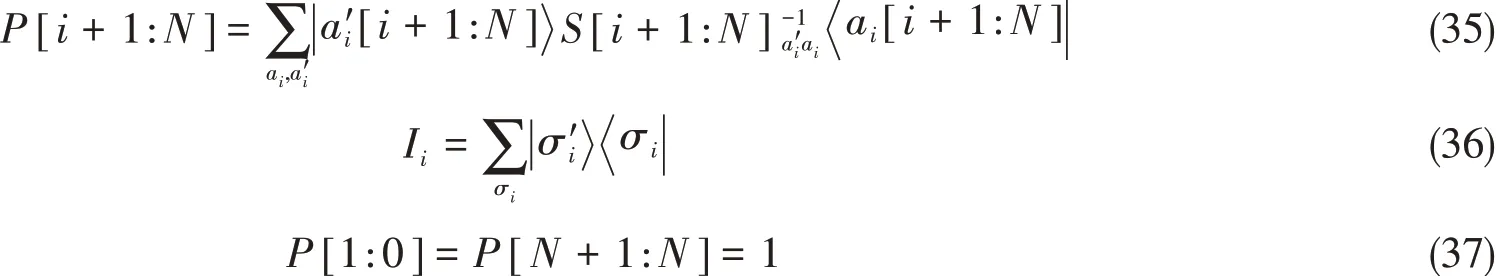
图3为式(33)的图形表示.重叠矩阵的逆S-1是由重正化基的非正交性导致的,而减号“-”里的项是为了消除参数冗余性[19,59].

Fig.3 Graphical representation of the tangent space projector
两种基于TDVP的时间演化方式区别在于在解式(32)时采用了不同的MPS规范条件.在第1种时间演化方案中,MPS的规范条件不发生改变.为方便起见,可以将除i=n的一个“+”项之外其它相邻“+”项和“-”项合并,如此每一项都是正交的,将式(33)中的投影算符转变为

其中
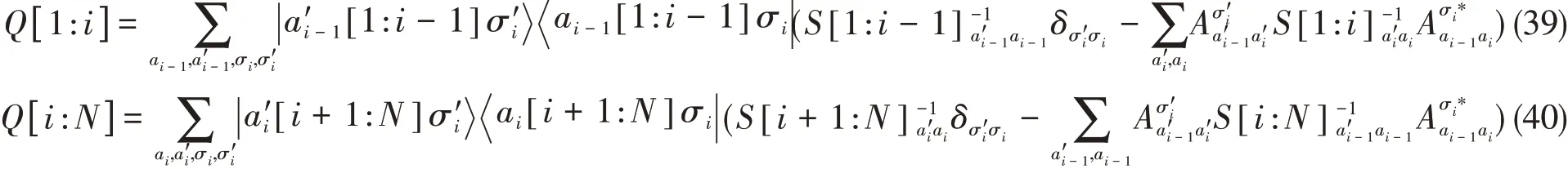
这种形式的投影算符及其相应的切空间向量首先由Haegeman等[19]针对均一MPS(Uniform MPS,uMPS)提出,Wouters等[59]对其进行了重新描述以推导一些针对基态和激发态的Post-DMRG算法.
如果采取一定的规范条件,式(39)和式(40)中的一些重叠矩阵将变成单位阵,表达式可以得到简化.假设当前MPS是左规整的,规整中心在第N个矩阵处,则S[1:i]简化为I,且在式(38)中设n=N最为简便.将简化后的投影算符代入式(32)得:

其中


式(41)和式(42)构成了一组耦合的非线性方程,与(ML-)MCTDH中标准的运动方程十分类似[28~30].(ML-)MCTDH中有两种典型的时间演化方案,一种称为可变平均场(Variable mean field,VMF),另一种称为常数平均场(Constant mean field,CMF).这两种方案也可用于对式(41)和式(42)进行积分[37].VMF使用普适的初值算法如前向欧拉法直接求解这些耦合方程.TDVP首先应用于MPS时即采用的这种方案[19].CMF则假设H[i]和S[i+1:N]比起CσN,Lσi的变化速率慢很多.因此在时间步τ中,“平均场”H[i],S[i+1:N]可以认为是常数,而演化局域矩阵CσN,Lσi.CMF因而可以被认为是VMF的一种近似.
这种固定规范条件的演化算法中,对S求逆的运算需要特别注意,因为如果S的一些特征值很小,对S求逆将会是数值不稳定的.当体系仅仅处于弱关联状态或虚拟键维数非常大时,比如体系处于Hartree直积态时,该问题会变得比较严重.在某种程度上,这种数值不稳定问题使得这种时间演化算法处于一种悖论中:使用更大的虚拟键维数原则上应该使计算结果更精确,然而如果时间步长不改变的话,使用更大的虚拟键维数实际上会使结果变得更不精确.相同的问题在(ML)-MCTDH中也会出现,为了使运动方程积分更稳定,S一般由一个正则化的重叠矩阵代替[29]:

式中:ε是一个小标量,一般取值为10-8~10-14.最近,Meyer和Wang[60,61]提出了一种基于对系数矩阵进行SVD矩阵展开(Matrix unfolding,MU)的改进(ML-)MCTDH正则化方式.这种正则化方式可以使时间积分算法更加精确和稳定(Robust).相同的方式可被用于积分式(42),这种时间演化算法称为TDVPMU[37].当计算重叠矩阵时,可以将当前MPS的一份拷贝的规范中心移动到第i+1个矩阵,且该矩阵可进一步被SVD分解:

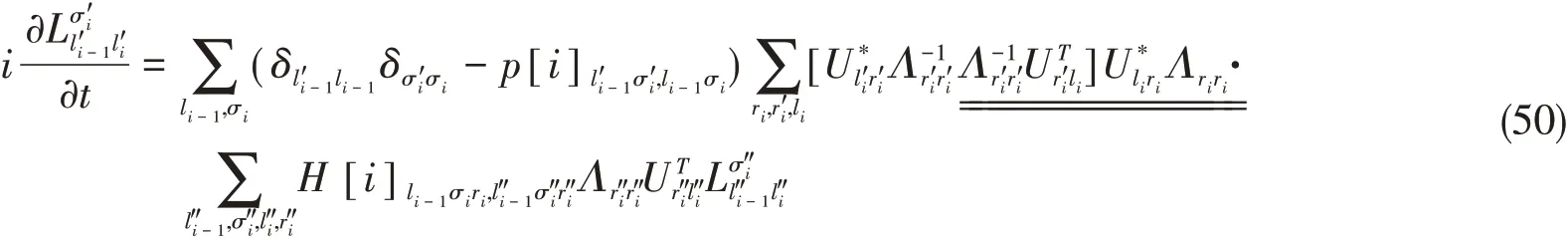
其中,“[…]”中的表达式正是S[i+1:N]-1.这种新的正则化方式的关键点在于具有下划线的部分可以

此处的1/2次方是为了与式(48)中原本的正则化方式保持一致.式(50)中的则保持不变,以减少对运动方程的影响,与MCTDH文献中的做法一致[60,61].尽管在MU中需要对环境做规整化,进行时间演化的MPS的规范条件保持不变.
第2种基于TDVP的时间演化方案是投影算符裂分法(PS).投影算符裂分的基础在于式(33)中的各项投影算符可以采取不同的规范条件.在对一个一般的MPS做从第N个矩阵到第i+1个矩阵的规整化后成为了右侧的重正化的基,与的关系如下:

通过QR分解得到的矩阵D是上三角矩阵.因此,重叠矩阵S[i+1:N]等于D*DT,而式(3)中对于一个一般的MPS定义的投影算符P[i+1:N]变形为
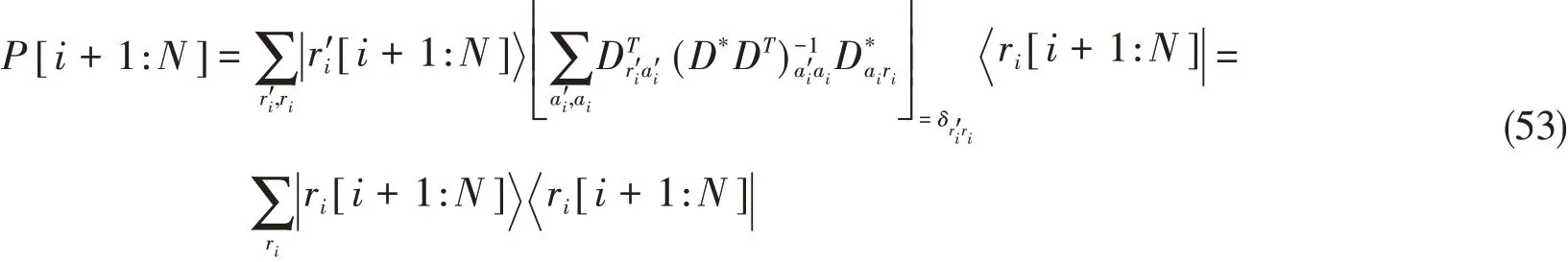
对于P[1:i]同理可得:

如此定义的切空间投影算符不含有求重叠矩阵逆的运算,似是对式(34)和式(35)的重大改进.然而,因为在这种定义方式中规范条件对于不同项的投影算符是不同的,上述介绍的VMF和CMF积分方式不再适用.Lubich和Haegeman等建议使用对称二阶Trotter分解将时间演化算符裂分成单独的项[20,62]:

基于式(55)中的时间演化算符,一步时间演化包括了一次从左向右的扫描以及随后的从右向左的扫描,两次扫描的时间步长均是τ/2.以从左向右的扫描为例,位于规整中心的矩阵首先通过作用进行正向时间演化:

其中,H[i]及其组成部分具有与式(43),式(44),式(45),式(46)相同的定义,只是式(46)中的Aσi被替换成为Lσi或者Rσi.然后,时间演化后的矩阵通过QR分解得到左规整的矩阵和系数矩阵通过作用投影算符P[1:i]⊗P[i+1:N]进行逆向时间演化:

与搜索基态的双格点DMRG算法类似,TDVP-PS也可以采用双格点的算法,使得虚拟键维数可以随体系纠缠熵的增长而增长.双格点算法在数值上也比单格点的算法更加稳定[17,51].但是,与基态算法类似,双格点算法比单格点算法计算量大很多.
TDVP-MU和TDVP-PS都是基于含时变分原理,当不考虑数值误差时,两者给出的时间演化结果应该是一样的.与P&C类算法相比,TDVP-MU以及单格点的TDVP-PS都需要提前指定一个固定的虚拟键维数,且如果当初态关联很弱时,需要构建额外的重正化基加入MPS.双格点的TDVP-PS一般不需要构建额外的重正化基使虚拟键维数达到指定的数值,因为在进行每两个格点的时间演化时需要对代表两个格点的矩阵做SVD,这就允许动态调整这两个格点之间虚拟键维数.TDVP-MU和TDVP-PS的主要区别是TDVP-MU需要进行额外的正则化,而TDVP-PS则不需要.
2.3 时间步瞄准算法
时间步瞄准(TST)算法主要是受同时求解基态和少数几个低能激发态的态平均DMRG算法启发,其数学基础不像前文介绍的算法那样严格[15,17].本文仅简要介绍其基本思想.

此时,整体波函数仍然表示体系在t时刻的状态,仅第i个矩阵所表示的重正化基依据从t到t+τ的时间步中的状态进行了更新.这一步更新不是严格的,会引入一定的误差.这一扫描过程不断进行直到收敛,而此时MPS的基被认为是能同时很好地描述t时刻与t+τ时刻的状态.此后,在规整中心进行真正的时间演化,完成MPS整体的一步时间演化.
3 有限温度算法
化学问题多与温度相关,如在以电声耦合模型来描述的输运现象中,温度起到了非常重要的作用,需要从量子统计的混合态的角度加以考虑.在波函数框架的TD-DMRG形式中有两种方式可以考虑温度带来的混合态问题,第1种为纯化(Purification)或辅助物(Ancilla)或热场动力学(Thermal field dynamics),适合高温和常温下的情形[63,64].第2种为最小纠缠典型量子热态(Minimally entangled typical thermal state,METTS)方法,主要适合低温下的情形[53,65].这两种方法也可以结合使用[66].需要指出的是,这两种方法都不是专门为TD-DMRG或MPS设计的,而是适用于各种基于波函数的方法.对于化学问题,纯化方法是最常用的一种直接了当的计算方法.
3.1 在扩增的希尔伯特空间纯化混合态的算法
纯化方法的核心是将混合态(密度矩阵)在扩增的希尔伯特空间表示为纯态(波函数)[63,64,67].对于任意物理量O,其有限温度期望的表达式为


而这正是需要用密度矩阵描述温度效应的理由.由于MPS是一种波函数的拟设,因此最好避免使用密度矩阵,用一个符合式(60)的波函数来描述体系性质.这一目标可以由将辅助Q空间引入P空间得到.Q空间的结构与P空间完全相同,可以定义相同的状态和算符.如果Q空间的能量本征态由上波浪线来表示那么构成了扩增的希尔伯特空间的一组正交归一完备基.定义如下的扩增的希尔伯特空间中的波函数



由于O仅作用于P空间,容易证明满足式(60).如果需要,热平衡态的密度矩阵可以由ΨPQ对Q求偏迹(或偏内积)构造:可以从P和Q空间的“单位状态出发进行虚时演化计算得到:在任意基组下的形式都相同,所以可采取易于计算的基组,事先并不需要计算配分函数也不需要显式地计算出来,因为也被称为最大纠缠态,因为P空间和Q空间之间的纠缠达到最大.由于其可以当做是的归一化系数.在每一步虚时间演化后进行归一化也可以解决波函数的模在虚时演化中不守恒的问题.在获得后,可以对其进行实时间演化,以获得所需的实时性质.原则上,开展实时演化和虚时演化的顺序是可以交换的,但实际上,先进行虚时演化再实时演化的计算效率更高,此外先进行虚时演化得到有利于对体系的热平衡态的性质进行分析.
虚时演化初始态I具有最大纠缠的事实对TD-DMRG计算具有不利影响,因为纠缠越大,MPS所需的虚拟键维数和计算量就越大.实际上,之所以有限温度计算的计算量一般比零温度计算大得多(特别是在有振动自由度的时候),不仅是因为纯化后自由度的数目翻倍,更是因为虚时演化和实时演化所需要的虚拟键维数一般比零温度大很多.幸运的是,在化学中常出现的一类电声耦合问题中,振动由独立的简谐振子描述,且体系初态处于电子和振动相互不关联的态,其中振动处于热平衡态.此时可以对振动自由度的PQ空间进行基变换,消除PQ空间之间的纠缠[68,69].设电子自由度处于基态而体系的振动处于热平衡态,则体系总的密度矩阵为


式(61)定义的纯化后的热平衡态与对扩展空间的基态进行一个酉变换的结果相同[67]:

其中G的形式为


以化学中常见的Holstein-Peierls哈密顿为例:

经过基变换后的哈密顿形式为

3.2 最小纠缠典型量子热态算法
低温下,纯化方法的效率较低.在β→∞极限,一方面,热平衡态实质上就是基态,因此纯化引入的Q空间成为了MPS表示的累赘,另一方面,β→∞本身就意味着需要做无穷多步的虚时演化[16].最小纠缠典型量子热态(METTS)方法是一种基于采样的方法,可以避免纯化,在低温下效率较高[53,65].
METTS方法的出发点是典型量子热态(TTS)的概念.式(59)是有限温度的物理量期望O在能量基下的表示.而对于任意完备正交归一的基期望的表达式为

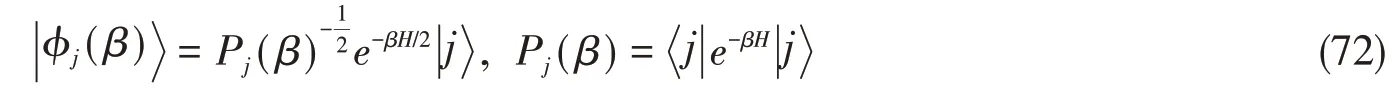

其中,n表示不同的自由度.这么做的原因是(尽管不严格):假如虚时间演化初态具有最小的纠缠,那么很可能典型量子热态也具有比较小的纠缠.METTS可以通过Markov链Monte-Carlo采样的方式进行采样,无需计算转移到的概率是设在一步Markov采样中,所有的态都已经具有正确的概率那么依据上述转移概率,在下一步迭代中,转移到某个态的概率为

而这正是所需要的正确概率.不动点的存在意味着在足够多步之后Markov采样将会收敛到正确的概率.另一个针对MPS的高效采样技巧是通过逐个格点的方式从塌缩至
4 TD-DMRG在化学中的应用
下面将介绍若干类TD-DMRG已经得到成功应用的化学科学问题.首先将聚焦于电声耦合模型中的非绝热动力学问题,随后将介绍基于第一性哈密顿的电子动力学问题.
4.1 激子及电荷转移动力学
激子动力学和电荷转移动力学对于生物分子和新材料中的能量和电荷转移至关重要.这类模型一般是由Frenkel-Holstein哈密顿及其变种所描述.在光合作用过程中,具有光学活性的生物分子吸收光子,形成激子.随后,太阳能通过分子间的激子耦合高效地转移至反应中心,储存为化学能.从分子层面上理解这一能量转移机制可以为优化和设计人造光合系统以及光电器件提供有益的信息.2013年,Plenio等[56]使用TD-DMRG研究了典型的色素-蛋白复合物Fenna-Matthews-Olson(FMO)复合物中的激子动力学过程.他们使用一个两色素模型,将哈密顿变换成只具有最近邻相互作用的等效哈密顿,然后利用TEBD算法进行时间演化[54].后来,Gelin和Borrelli利用TDVP-PS算法,将这一研究拓展到具有7个色素的模型以及反应中心的电子转移模型[50,71].Gelin等的研究通过纯化结合Bogoliubov变换的方式考虑了有限温度效应.他们还在TD-DMRG的辅助下证明了具有静态无序的等价色素体系的长时间动力学由振动动力学所控制[72].
利用TD-DMRG也可以对有机太阳能电池中给体/受体界面的超快激子分离问题做类似的理论模拟[21,22].激子分离的模型中除了激子态和电声耦合之外一般还包括电荷转移态.Ma等[21]在不同电声耦合强度α下,用TD-DMRG计算了空穴(给体部分)和电子(受体部分)密度随时间的演化(图4),其中电声耦合由声子谱密度是截止频率)所刻画.可见,在适中的电声耦合强度下,体系中存在超快的长程电荷转移.他们将这一现象归因于局域Frenkel激子态和长程电荷转移态之间的量子共振.

Fig.4 Charge density evolution of hole in the donor part and electron in the acceptor part with differentαvalues[21]
除了上述报道以外,还有针对π共轭高分子如聚对亚苯(PPP)和聚对苯撑乙烯(PPV)体系中超快激子弛豫、退相干和局域化的研究[57,73].如果将三线态对纳入到电子基组中,基于三态或更复杂的模型,TD-DMRG也可以用于研究单态裂分过程[51,74].
这类针对激子动力学(或电荷转移动力学)的理论模拟一般分为3步.首先将系统中没有激子(或电荷)的零温度纯态或热平衡态表示成一个MPS,此时系统中各个自由度往往没有关联.然后,通过将产生算符作用在系统上的方式将一个激子(或电荷)注入到合适的分子上.最后就是通过合适的时间演化算法进行系统的时间演化,并在每一时间步计算关键的物理量如电子的约化密度矩阵元.需要注意的是,根据一项最近使用TD-DMRG的研究,上述步骤中描述的垂直Franck-Condon激发动力学与从振动弛豫的激发态出发的动力学可能完全不同[52].此外,只要振动自由度是由简谐振子所描述的,采用Bogoliubov变换是考虑有限温度效应的有效方式.
4.2 激发态动力学及光谱
激发态动力学与激子动力学实际上密不可分,本文描述的激发态动力学主要关注基于复杂势能面的动力学或与光谱直接相关的动力学.复杂势能面动力学的典型代表是紫外光激发吡嗪分子至S2态后S1/S2的内转换动力学.这一问题已被包括MCTDH在内的许多非绝热动力学方法所研究[75,76].吡嗪分子共有24个正则振动模式,电声耦合较强,在S1态S2态之间存在一个锥形交叉点.因此该体系的动力学是量子动力学方法的一个严格的基准测试.基于线性响应理论,分子的吸收光谱I(ω)可以由偶极-偶极关联函数C(t)的傅里叶变换得到:

式中:μ为偶极算符;下角标g代表基态.在零温度下,计算C(t)可以简化成计算时间演化的波函数Ψ(t)与初始S2态波函数Ψ(0)的重叠:

此处,Eg是基态能量,通过恰当地定义哈密顿,可以使其为能量零点.P&C和基于TDVP的时间演化算法都可以用于处理这一时间演化问题[24,47,51].这些时间演化算法与高精度的电子结构方法导出的第一性参数相结合,可以模拟出与实验结果相吻合的光谱.
同样的方法也可推广到分子聚集体,如苝酰亚胺染料(PBI)的光谱[23,24].对算法稍作调整后,也可以计算有限温度的光谱[23].这一调整的关键是在计算C(t)时,对纯化后的热平衡态同时开展两组时间演化:


Fig.5 Calculated absorption and fluorescence spectra of PBI dimer at 298 K from finite temperature TD-DMRG[23]
4.3 电荷输运
共轭高分子中的电荷输运性质是TD-DMRG在化学中的最早应用之一[55,78,79].这些工作在利用TD-DMRG描述电子运动的同时,利用经典力学描述核的运动,形成了一种混合TD-DMRG/Ehrenfest时间演化方法.近期,我们[25]利用另一种思路即Kubo方程计算了有限温度下有机半导体中的载流子电荷迁移率:

其中j是电流算符,凭借我们[80]最近开发的自动化构建MPO的方法,可以精确地表示成MPO[25].图6展示了由TD-DMRG计算得到的红荧烯晶体迁移率和由费米黄金规则(Fermi’s golden rule,FGR)和玻尔兹曼输运理论(Boltzmann transport theory)得到的迁移率的对比.可以看出,在跳跃极限下即转移积分V比较小时,TD-DMRG可以回归到FGR的解析结果.而在能带极限下即转移积分V比较大时,TD-DMRG的渐进行为与Boltzmann输运理论相同.除此之外,TD-DMRG计算的迁移率还符合实验观察到的“类能带”传输行为以及负的同位素效应[25].

Fig.6 Carrier mobility from weak to strong electronic coupling(V)calculated by TD-DMRG,FGR(hopping limit),and Boltzmann transport theory(band limit)(A),mean free path(l mfp)of the charge carrier from weak to strong electronic coupling calculated by TD-DMRG(B)[25]
4.4 电子动力学
尽管大多数化学中的TD-DMRG文献以电声耦合模型作为研究的对象,由于TD-DMRG是一种普适的方法,在最近的文献中出现了纯电子动力学研究.如Chan等[38]利用改进的TST算法和频域DMRG算法研究了一维氢原子链的动态性质,基于第一性原理哈密顿计算了体系的态密度和复极化函数,以作为不同键长时体系的金属性和离域性的判据.最近,Frahm等[39]利用TD-DMRG模拟了碘乙炔分子中基于第一性原理哈密顿的超快电荷转移动力学,其结果如图7所示.初始时刻,空穴布居在碘上,随后空穴转移到碳上,然后又回到碘上,最后空穴再次布居在碳上,与实验测量结果直接符合.

Fig.7 Hole density(red)of the iodoacetylene molecule at four different points in time[39]
5 总结与展望
本文介绍了TD-DMRG的关键算法及近期TD-DMRG在化学问题中的应用.受益于现代DMRG精巧而简洁的MPS数学结构,越来越多的TD-DMRG时间演化算法不断涌现,这些算法各自具有不同的特点,需要使用者针对合适的问题选择合适的算法.两种使TD-DMRG可以考虑温度效应的算法进一步增强了TD-DMRG模拟真实体系的能力.丰富的应用说明,TD-DMRG可以精确地模拟许多动态过程,如分子聚集体和生物体系中的激子动力学、单态裂分、小分子和聚集体的一维和二维光谱、有机半导体的电荷输运以及基于第一性原理的电子动力学等.由于矩阵乘积的数学形式简洁,未来,MPS可能会与机器学习的方法相结合用于拟合实际分子的势能面,并在TD-DMRG的框架下发展多原子体系的量子动力学和光谱的计算方法.另外,现有的TD-DMRG计算电荷传输迁移率的方法可以很方便地推广到热输运、自旋输运以及热电转换等问题,具有非常广阔的应用空间.然而,超越一维模型是TD-DMRG模拟实际块体材料所面对的主要挑战.高维模型的计算量一般比一维模型大很多,对高维模型的高效模拟仍然有赖于进一步发展TD-DMRG方法.
TD-DMRG的一个主要不足是对最大演化时长的限制.在常见的化学问题中,体系的二分纠缠熵S随演化时间线性增长S∝t[81,82].这意味着数值精确的模拟所需要的虚拟键维数随时间指数增长M∝et,或者说如果虚拟键维数固定,时间演化的误差随时间指数增长[16].因此,总体上,TD-DMRG更适合于模拟超快过程的演化,而对长时间的演化问题仍需要发展新的算法.尽管如此,现有的TD-DMRG算法已经足够在相当长的演化时间内给出含时薛定谔方程的可靠解.一个可以绕开这一限制的策略是通过关联函数计算感兴趣的物理量(如迁移率),因为对于真实化学系统来说关联函数在长时间应该收敛到0.另一种策略是在频域空间计算体系性质[83].在TD-DMRG中直接克服这一纠缠障碍的方法现在仍在发展中[84].

